【人教九上数学学霸听课笔记】23.1.1 旋转的概念及性质 课件(共34张PPT)
文档属性
| 名称 | 【人教九上数学学霸听课笔记】23.1.1 旋转的概念及性质 课件(共34张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-18 00:00:00 | ||
图片预览








文档简介
(共34张PPT)
第1课时 旋转的概念及性质
预学浅梳理
探究与应用
随堂小检测
第二十三章 旋转
1.把一个平面图形绕着平面内某一点O转动一个角度,叫做
____________,________叫做旋转中心,转动的角叫做
________.
2.旋转的性质:
(1)对应点到旋转中心的距离________.
(2)对应点与旋转中心所连线段的夹角等于________.
(3)旋转前、后的图形________.
图形的旋转
点O
旋转角
相等
旋转角
全等
目标一 理解旋转的有关概念
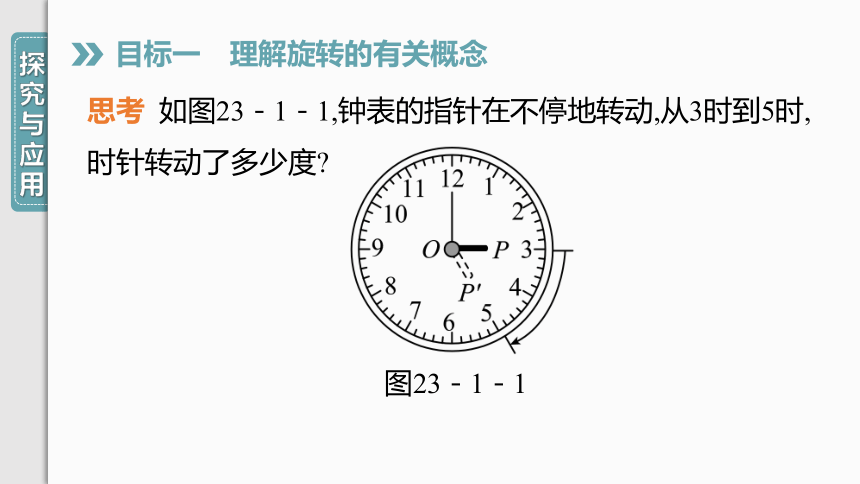
思考
如图23-1-1,钟表的指针在不停地转动,从3时到5时,时针转动了多少度?
图23-1-1
如图23-1-2,风车风轮的每个叶片在风的吹动下转动到新的位置.
以上这些现象有什么共同特点呢?
解:从3时到5时,时针转动了60°.
这些现象的共同特点是一个平面图形
绕着一点转动一个角度.
图23-1-2
定义
把一个平面图形绕着平面内某一点O转动一个角度,
叫做图形的旋转.图23-1-1中,点O是_________,旋转角是
________.点P和点P′是________.
图23-1-1
旋转中心
∠POP′
对应点
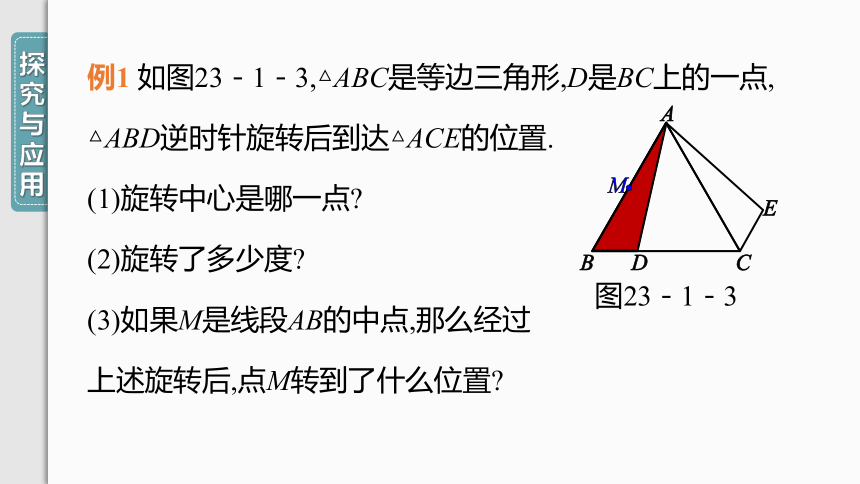
例1
如图23-1-3,△ABC是等边三角形,D是BC上的一点,
△ABD逆时针旋转后到达△ACE的位置.
(1)旋转中心是哪一点?
(2)旋转了多少度?
(3)如果M是线段AB的中点,那么经过
上述旋转后,点M转到了什么位置?
图23-1-3
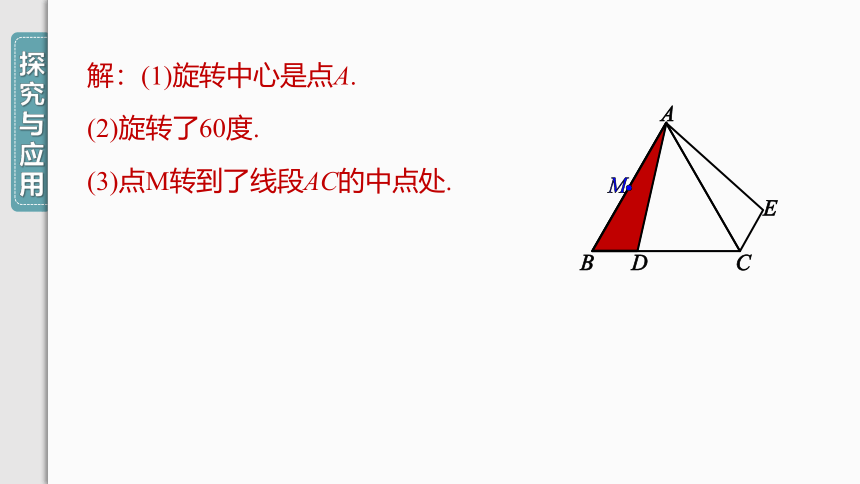
解:(1)旋转中心是点A.
(2)旋转了60度.
(3)点M转到了线段AC的中点处.
归纳
旋转的“三要素”及确定方法
(1)旋转中心:旋转中心的位置可以是任意的,旋转前后没有
发生变化的点就是旋转中心;
(2)旋转角:对应点与旋转中心所连线段的夹角即旋转角;
(3)旋转方向:旋转方向有顺时针和逆时针两种,若没有明确
指出旋转方向,则应分两种情况讨论.
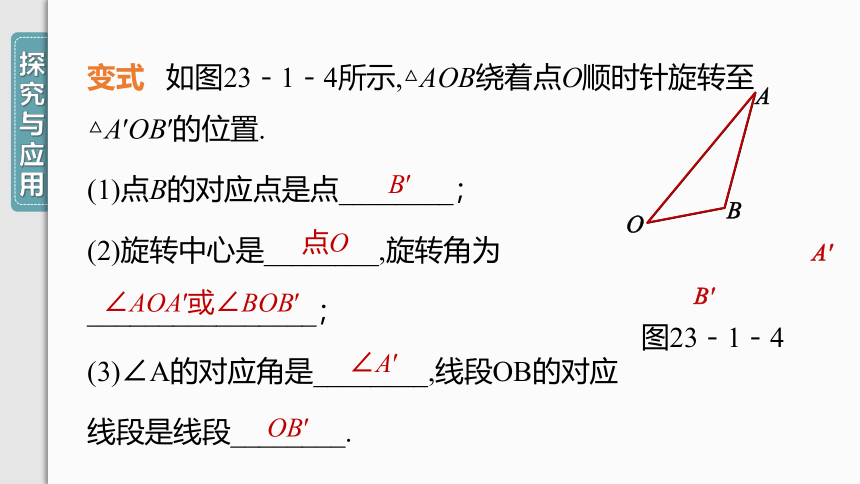
变式
如图23-1-4所示,△AOB绕着点O顺时针旋转至△A′OB′的位置.
(1)点B的对应点是点________;
(2)旋转中心是________,旋转角为
________________;
(3)∠A的对应角是________,线段OB的对应
线段是线段________.
图23-1-4
B′
点O
∠AOA′或∠BOB′
∠A′
OB′
目标二 理解并掌握旋转的性质
探究
如图23-1-5,在硬纸板上,挖一个三角形洞,再另挖一个小洞O作为旋转中心,硬纸板下面放一张白纸.先在纸上描出这个挖掉的三角形图案(△ABC),然后围绕旋转中心转动硬纸板,再描出这个挖掉的三角形(△A′B′C′),
移开硬纸板.
图23-1-5
△A′B′C′是由△ABC绕点O旋转得到的.线段OA与OA′有什么关系?∠AOA′与∠BOB′有什么关系?△ABC与△A′B′C′的形状和大小有什么关系?
解:OA=OA′,∠AOA′=∠BOB′,△ABC≌△A′B′C′.
图23-1-5
归纳
旋转的性质
(1)对应点到_________的距离相等.
(2)________与旋转中心所连线段的夹角等于旋转角.
(3)旋转前、后的图形________.
旋转中心
对应点
全等
例2
[教材P60例题]如图23-1-6,E是正方形ABCD中CD边上任意一点,以点A为中心,把△ADE顺时针旋转90°,画出旋转后的图形.请你尽可能多地说出你的画法.
图23-1-6
解:因为点A是旋转中心,所以它的对应点是它本身.
正方形ABCD中,AD=AB,∠DAB=90°,所以旋转后点D与点B重合.
设点E的对应点为点E′.
因为旋转后的图形与旋转前的图形全等,
所以∠ABE′=∠ADE=90°,BE′=DE.
方法一:在CB的延长线上取点E′,使BE′=DE,则△ABE′为旋转后的图形(如图).
方法二:以点A为圆心,以AE为半径画弧,交CB的延长线于点E′,则△ABE′为旋转后的图形.
方法三:过点A作E′A⊥AE,交CB的延长线于点E′,则△ABE′为旋转后的图形.
方法四:在正方形ABCD的外部作∠BAE′=∠DAE,交CB的延长线于点E′,则△ABE′为旋转后的图形.(本题画法较多,答案不唯一)
例3
如图23-1-7,△ABD,△AEC都是等边三角形.BE与DC有什么关系?你能用旋转的性质说明上述关系成立的理由吗?
解:BE=DC.
能.理由:∵△ABD,△AEC都是等边三角形,
∴AB=AD,AE=AC,∠BAD=∠EAC=60°,
∴△ABE可以看成是由△ADC绕点A逆时针旋转60°得到的.
又∵DC的对应线段是BE,∴BE=DC.
图23-1-7
可以从旋转角度看问题的图形的特征
当图中含有两个形状相同的图形(比如两个等边三角形,
两个正方形,两个等腰直角三角形等)时,可以从旋转的角度
将相等的边的关系看作是旋转而成的位置关系,进而找到部
分图形的旋转变换关系,从而利用旋转的相关性质解决问题.
方法总结
变式
如图23-1-8,如果点A在线段BC上,△ABD,△AEC都是等边三角形,那么BE与DC相等吗?
解:∵△ABD,△AEC都是等边三角形,
∴AB=AD,AE=AC,∠BAD=∠EAC=60°,
∴△ABE可以看成是由△ADC绕点A逆时针旋转60°得到的.
又∵DC的对应线段是BE,∴BE=DC.
图23-1-8
延伸
上题条件不变,若AD与BE交于点F,AE与CD交于点G,连接FG,如图J23-1-1.
(1)AF=AG吗?说明理由;
(2)△AFG是等边三角形吗?为什么?
图J23-1-1
解:(1)AF=AG.
理由如下:
由变式易知△ABE≌△ADC,
∴∠ABE=∠ADC.
∵△ABD和△AEC都是等边三角形,
∴AB=AD,∠BAD=∠EAC=60°,
∴∠DAG=60°=∠BAF.
∴△ABF≌△ADG(ASA),
∴AF=AG.
(2)△AFG是等边三角形.理由如下:
∵AF=AG,且∠DAG=60°,
∴△AFG是等边三角形.
1.下列运动中,不属于旋转的是( )
A.人荡秋千时的运动
B.人行走时手臂的运动
C.跳远运动
D.仰卧起坐运动
C
2.如图23-1-9所示,在Rt△ABC中,∠BAC=90°,∠B=60°,△AB′C′可以由△ABC绕点A顺时针旋转90°得到(点B′与点B是对应点,点C′与点C是对应点),连接CC′,则∠CC′B′的度数是( )
A.45°
B.30°
C.25°
D.15°
图23-1-9
D
[解析]
由旋转中心为点A,点C与点C′为对应点可知AC=AC′.又由∠CAC′=90°可知△CAC′是等腰直角三角形,所以∠CC′A=45°.又由∠AC′B′=∠ACB=90°-60°=30°,可得∠CC′B′=15°.
3.如图23-1-10,将△ABC绕点A逆时针旋转得到△ADE,点C和点E是对应点,点B和点D是对应点,若∠CAE=90°,AB=1,则BD=________.
图23-1-10
4.如图23-1-11,在Rt△ABC中,∠ACB=90°,点D,F分别在AB,AC上,CF=CB.连接CD,将线段CD绕点C按顺时针方向旋转90°后得CE,连接EF.
(1)求证:△BCD≌△FCE;
(2)若EF∥CD,求∠BDC的度数.
图23-1-11
解:(1)证明:∵CD绕点C按顺时针方向旋转90°后得CE,
∴CD=CE,∠DCE=90°.
∵∠ACB=90°,∴∠BCD=90°-∠ACD=∠FCE.
∴△BCD≌△FCE.
(2)由△BCD≌△FCE得∠BDC=∠E.
∵EF∥CD,∴∠E=180°-∠DCE=90°,
∴∠BDC=90°.
https://www.21cnjy.com/help/help_extract.php
第1课时 旋转的概念及性质
预学浅梳理
探究与应用
随堂小检测
第二十三章 旋转
1.把一个平面图形绕着平面内某一点O转动一个角度,叫做
____________,________叫做旋转中心,转动的角叫做
________.
2.旋转的性质:
(1)对应点到旋转中心的距离________.
(2)对应点与旋转中心所连线段的夹角等于________.
(3)旋转前、后的图形________.
图形的旋转
点O
旋转角
相等
旋转角
全等
目标一 理解旋转的有关概念
思考
如图23-1-1,钟表的指针在不停地转动,从3时到5时,时针转动了多少度?
图23-1-1
如图23-1-2,风车风轮的每个叶片在风的吹动下转动到新的位置.
以上这些现象有什么共同特点呢?
解:从3时到5时,时针转动了60°.
这些现象的共同特点是一个平面图形
绕着一点转动一个角度.
图23-1-2
定义
把一个平面图形绕着平面内某一点O转动一个角度,
叫做图形的旋转.图23-1-1中,点O是_________,旋转角是
________.点P和点P′是________.
图23-1-1
旋转中心
∠POP′
对应点
例1
如图23-1-3,△ABC是等边三角形,D是BC上的一点,
△ABD逆时针旋转后到达△ACE的位置.
(1)旋转中心是哪一点?
(2)旋转了多少度?
(3)如果M是线段AB的中点,那么经过
上述旋转后,点M转到了什么位置?
图23-1-3
解:(1)旋转中心是点A.
(2)旋转了60度.
(3)点M转到了线段AC的中点处.
归纳
旋转的“三要素”及确定方法
(1)旋转中心:旋转中心的位置可以是任意的,旋转前后没有
发生变化的点就是旋转中心;
(2)旋转角:对应点与旋转中心所连线段的夹角即旋转角;
(3)旋转方向:旋转方向有顺时针和逆时针两种,若没有明确
指出旋转方向,则应分两种情况讨论.
变式
如图23-1-4所示,△AOB绕着点O顺时针旋转至△A′OB′的位置.
(1)点B的对应点是点________;
(2)旋转中心是________,旋转角为
________________;
(3)∠A的对应角是________,线段OB的对应
线段是线段________.
图23-1-4
B′
点O
∠AOA′或∠BOB′
∠A′
OB′
目标二 理解并掌握旋转的性质
探究
如图23-1-5,在硬纸板上,挖一个三角形洞,再另挖一个小洞O作为旋转中心,硬纸板下面放一张白纸.先在纸上描出这个挖掉的三角形图案(△ABC),然后围绕旋转中心转动硬纸板,再描出这个挖掉的三角形(△A′B′C′),
移开硬纸板.
图23-1-5
△A′B′C′是由△ABC绕点O旋转得到的.线段OA与OA′有什么关系?∠AOA′与∠BOB′有什么关系?△ABC与△A′B′C′的形状和大小有什么关系?
解:OA=OA′,∠AOA′=∠BOB′,△ABC≌△A′B′C′.
图23-1-5
归纳
旋转的性质
(1)对应点到_________的距离相等.
(2)________与旋转中心所连线段的夹角等于旋转角.
(3)旋转前、后的图形________.
旋转中心
对应点
全等
例2
[教材P60例题]如图23-1-6,E是正方形ABCD中CD边上任意一点,以点A为中心,把△ADE顺时针旋转90°,画出旋转后的图形.请你尽可能多地说出你的画法.
图23-1-6
解:因为点A是旋转中心,所以它的对应点是它本身.
正方形ABCD中,AD=AB,∠DAB=90°,所以旋转后点D与点B重合.
设点E的对应点为点E′.
因为旋转后的图形与旋转前的图形全等,
所以∠ABE′=∠ADE=90°,BE′=DE.
方法一:在CB的延长线上取点E′,使BE′=DE,则△ABE′为旋转后的图形(如图).
方法二:以点A为圆心,以AE为半径画弧,交CB的延长线于点E′,则△ABE′为旋转后的图形.
方法三:过点A作E′A⊥AE,交CB的延长线于点E′,则△ABE′为旋转后的图形.
方法四:在正方形ABCD的外部作∠BAE′=∠DAE,交CB的延长线于点E′,则△ABE′为旋转后的图形.(本题画法较多,答案不唯一)
例3
如图23-1-7,△ABD,△AEC都是等边三角形.BE与DC有什么关系?你能用旋转的性质说明上述关系成立的理由吗?
解:BE=DC.
能.理由:∵△ABD,△AEC都是等边三角形,
∴AB=AD,AE=AC,∠BAD=∠EAC=60°,
∴△ABE可以看成是由△ADC绕点A逆时针旋转60°得到的.
又∵DC的对应线段是BE,∴BE=DC.
图23-1-7
可以从旋转角度看问题的图形的特征
当图中含有两个形状相同的图形(比如两个等边三角形,
两个正方形,两个等腰直角三角形等)时,可以从旋转的角度
将相等的边的关系看作是旋转而成的位置关系,进而找到部
分图形的旋转变换关系,从而利用旋转的相关性质解决问题.
方法总结
变式
如图23-1-8,如果点A在线段BC上,△ABD,△AEC都是等边三角形,那么BE与DC相等吗?
解:∵△ABD,△AEC都是等边三角形,
∴AB=AD,AE=AC,∠BAD=∠EAC=60°,
∴△ABE可以看成是由△ADC绕点A逆时针旋转60°得到的.
又∵DC的对应线段是BE,∴BE=DC.
图23-1-8
延伸
上题条件不变,若AD与BE交于点F,AE与CD交于点G,连接FG,如图J23-1-1.
(1)AF=AG吗?说明理由;
(2)△AFG是等边三角形吗?为什么?
图J23-1-1
解:(1)AF=AG.
理由如下:
由变式易知△ABE≌△ADC,
∴∠ABE=∠ADC.
∵△ABD和△AEC都是等边三角形,
∴AB=AD,∠BAD=∠EAC=60°,
∴∠DAG=60°=∠BAF.
∴△ABF≌△ADG(ASA),
∴AF=AG.
(2)△AFG是等边三角形.理由如下:
∵AF=AG,且∠DAG=60°,
∴△AFG是等边三角形.
1.下列运动中,不属于旋转的是( )
A.人荡秋千时的运动
B.人行走时手臂的运动
C.跳远运动
D.仰卧起坐运动
C
2.如图23-1-9所示,在Rt△ABC中,∠BAC=90°,∠B=60°,△AB′C′可以由△ABC绕点A顺时针旋转90°得到(点B′与点B是对应点,点C′与点C是对应点),连接CC′,则∠CC′B′的度数是( )
A.45°
B.30°
C.25°
D.15°
图23-1-9
D
[解析]
由旋转中心为点A,点C与点C′为对应点可知AC=AC′.又由∠CAC′=90°可知△CAC′是等腰直角三角形,所以∠CC′A=45°.又由∠AC′B′=∠ACB=90°-60°=30°,可得∠CC′B′=15°.
3.如图23-1-10,将△ABC绕点A逆时针旋转得到△ADE,点C和点E是对应点,点B和点D是对应点,若∠CAE=90°,AB=1,则BD=________.
图23-1-10
4.如图23-1-11,在Rt△ABC中,∠ACB=90°,点D,F分别在AB,AC上,CF=CB.连接CD,将线段CD绕点C按顺时针方向旋转90°后得CE,连接EF.
(1)求证:△BCD≌△FCE;
(2)若EF∥CD,求∠BDC的度数.
图23-1-11
解:(1)证明:∵CD绕点C按顺时针方向旋转90°后得CE,
∴CD=CE,∠DCE=90°.
∵∠ACB=90°,∴∠BCD=90°-∠ACD=∠FCE.
∴△BCD≌△FCE.
(2)由△BCD≌△FCE得∠BDC=∠E.
∵EF∥CD,∴∠E=180°-∠DCE=90°,
∴∠BDC=90°.
https://www.21cnjy.com/help/help_extract.php
同课章节目录
