1.1菱形的性质与判定 同步能力达标测评 2021-2022学年北师大版九年级数学上册(Word版 含答案)
文档属性
| 名称 | 1.1菱形的性质与判定 同步能力达标测评 2021-2022学年北师大版九年级数学上册(Word版 含答案) |
|
|
| 格式 | doc | ||
| 文件大小 | 395.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-18 00:00:00 | ||
图片预览



文档简介
2021-2022学年北师大版九年级数学上册《1.1菱形的性质与判定》
同步能力达标测评(附答案)
一.选择题(共8小题,每小题4分,共计32分)
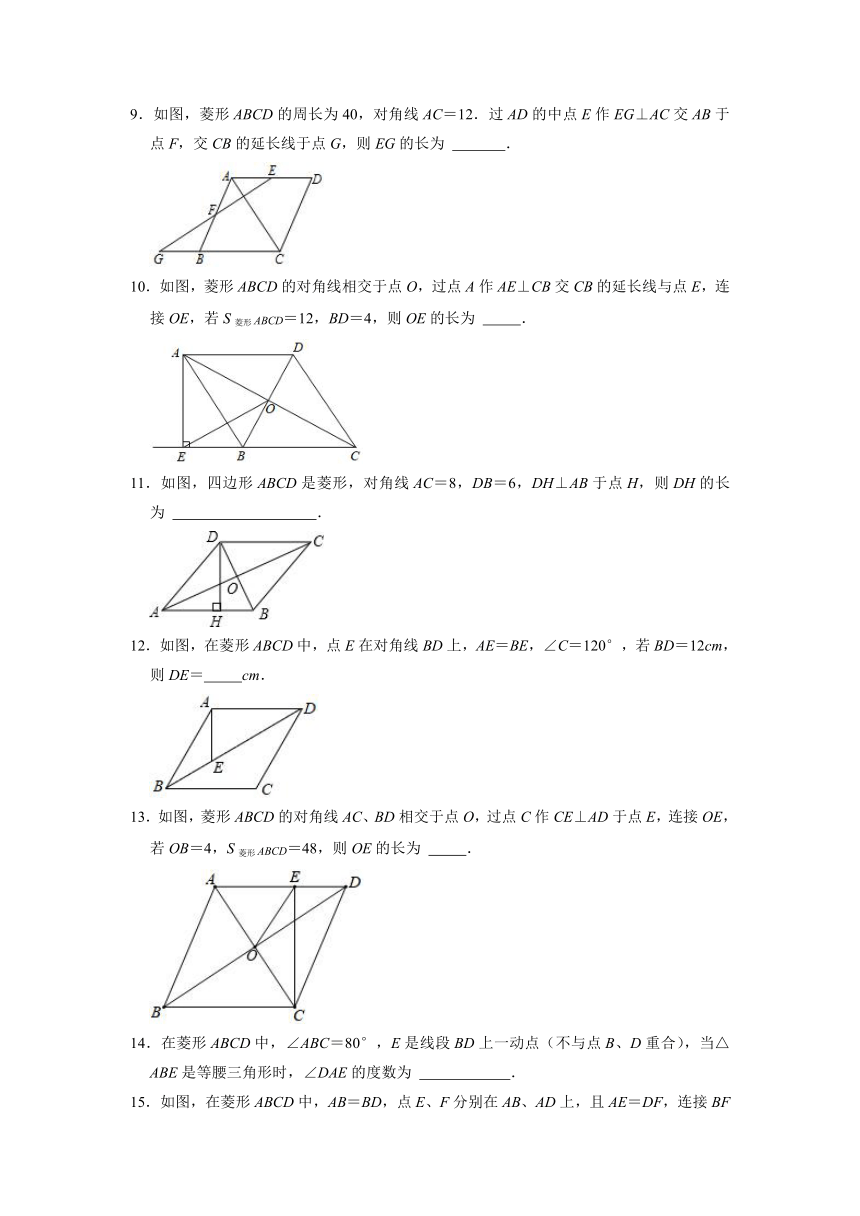
1.如图,在平面直角坐标系xOy中,菱形ABCD的顶点D在x轴上,边BC在y轴上,若点A的坐标为(2,3),则C点的坐标为( )
A.(0,﹣2)
B.(0,﹣1.5)
C.(0,﹣1)
D.(﹣2,0)
2.如图,在菱形ABCD中,∠ABC=50°,对角线AC,BD交于点O,E为CD的中点,连接OE,则∠AOE的度数是( )
A.110°
B.112°
C.115°
D.120°
3.如图,AC是菱形ABCD的对角线,P是AC上一个动点,过点P分别作AB、BC的垂线,垂足分别是F和E.若菱形ABCD的周长是12cm,面积是6cm2,则PE+PF的值是( )
A.1.5
B.1
C.2
D.4
4.四边形ABCD中,AD∥BC,点P,Q是对角线BD上不同的两点,若四边形APCQ是菱形,则下列说法中不正确的是( )
A.BP=DQ
B.∠ABD=∠ADB
C.AB∥CD
D.∠ABP=∠BAP
5.如图四边形ABCD为菱形,点E为BC的中点,点F在CD上,若∠DAB=60°,∠DFA=2∠EAB,AD=4,则CF的长为( )
A.
B.
C.
D.
6.如图,菱形ABCD的边长为10,对角线AC=16,点E、F分别是边CD、BC的中点,连接EF并延长与AB的延长线相交于点G,则EG长为( )
A.13
B.10
C.12
D.5
7.如图,在菱形ABCD中,∠BAD=60°,AC与BD交于点O,E为CD延长线上的一点,且CD=DE,连接BE分别交AC、AD于点F、G,连接OG,则下列结论中一定成立的是( )
①OG=AB;②与△DEG全等的三角形共有5个;③四边形ODEG与四边形OBAG面积相等;④由点A、B、D、E构成的四边形是菱形.
A.①③④
B.①④
C.①②③
D.②③④
8.如图,两张等宽的纸条交叉叠放在一起,若重合部分构成的四边形ABCD中,AB=3,AC=2,则四边形ABCD的面积为( )
A.
B.
C.
D.5
二.填空题(共8小题,每小题4分,共计32分)
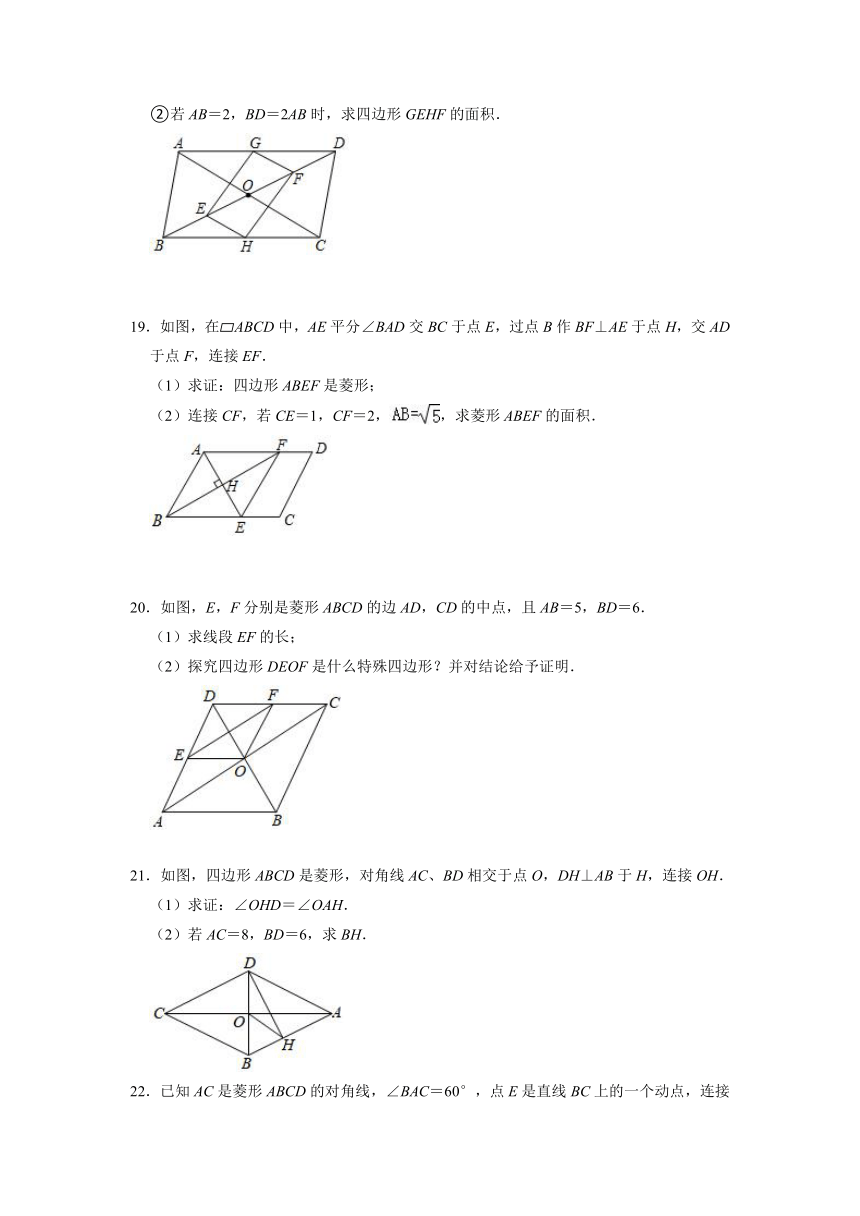
9.如图,菱形ABCD的周长为40,对角线AC=12.过AD的中点E作EG⊥AC交AB于点F,交CB的延长线于点G,则EG的长为
.
10.如图,菱形ABCD的对角线相交于点O,过点A作AE⊥CB交CB的延长线与点E,连接OE,若S菱形ABCD=12,BD=4,则OE的长为
.
11.如图,四边形ABCD是菱形,对角线AC=8,DB=6,DH⊥AB于点H,则DH的长为
.
12.如图,在菱形ABCD中,点E在对角线BD上,AE=BE,∠C=120°,若BD=12cm,则DE=
cm.
13.如图,菱形ABCD的对角线AC、BD相交于点O,过点C作CE⊥AD于点E,连接OE,若OB=4,S菱形ABCD=48,则OE的长为
.
14.在菱形ABCD中,∠ABC=80°,E是线段BD上一动点(不与点B、D重合),当△ABE是等腰三角形时,∠DAE的度数为
.
15.如图,在菱形ABCD中,AB=BD,点E、F分别在AB、AD上,且AE=DF,连接BF与DE交于点G,若CG=1,则S四边形BCDG=
.
16.我们定义:联结平行四边形一组对边中点的线段叫做“对边中位线”,联结平行四边形一组邻边中点的线段叫做“邻边中位线”.如图,在菱形ABCD中,∠A=60°,对角线BD=8,那么“对边中位线”EF与“邻边中位线”EG、FG所围成的△EFG的面积是
.
三.解答题(共7小题,每小题,8分,共计56分)
17.如图,点A,F,C,D在同一条直线上,点B,E分别在直线AD两侧,且AB=DE,∠A=∠D,AC=DF.
(1)求证:四边形BCEF是平行四边形,
(2)若∠ABC=90°,EF=3,AB=4,当CD为何值时,四边形BCEF是菱形.
18.已知:如图,在?ABCD中,对角线AC、BD相交于点O,点G、H分别是AD、BC的中点,点E、O、F分别是对角线BD上的四等分点,顺次连接G、E、H、F.
(1)求证:四边形GEHF是平行四边形;
(2)若四边形GEHF是菱形.
①线段AB和BD有何位置关系?请说明理由.
②若AB=2,BD=2AB时,求四边形GEHF的面积.
19.如图,在?ABCD中,AE平分∠BAD交BC于点E,过点B作BF⊥AE于点H,交AD于点F,连接EF.
(1)求证:四边形ABEF是菱形;
(2)连接CF,若CE=1,CF=2,,求菱形ABEF的面积.
20.如图,E,F分别是菱形ABCD的边AD,CD的中点,且AB=5,BD=6.
(1)求线段EF的长;
(2)探究四边形DEOF是什么特殊四边形?并对结论给予证明.
21.如图,四边形ABCD是菱形,对角线AC、BD相交于点O,DH⊥AB于H,连接OH.
(1)求证:∠OHD=∠OAH.
(2)若AC=8,BD=6,求BH.
22.已知AC是菱形ABCD的对角线,∠BAC=60°,点E是直线BC上的一个动点,连接AE,以AE为边作菱形AEFG,并且使∠EAG=60°,连接CG,当点E在线段BC上时,如图1,易证:AB=CG+CE.
(1)当点E在线段BC的延长线上时(如图2),猜想AB,CG,CE之间的关系并证明;
(2)当点E在线段CB的延长线上时(如图3),直接写出AB,CG,CE之间的关系.
23.如图1,已知平行四边形ABCD中,BD平分∠CBA.
(1)求证:平行四边形ABCD是菱形;
(2)如图2,E为边AB上一动点,连接CE,作CE的垂直平分线交CE于F,交DB于G,连接AG、EG,
①求证:△AGE为等腰三角形;
②若∠CBA=60°,求的值.
参考答案
一.选择题(共8小题,每小题4分,共计32分)
1.解:∵A(2,3),
∴OD=2,AD=3,
∵四边形ABCD是菱形,
∴CD=AD=3,
在Rt△ODC中,OC===1,
∴C(0,﹣1).
故选:C.
2.解:∵四边形ABCD是菱形,
∴AC⊥BD,∠CDO=∠ADC=∠ABC=25°,
∴∠DOC=90°,
∵点E是CD的中点,
∴OE=DE=CD,
∴∠DOE=∠CDO=25°,
∴∠AOE=∠AOD+∠DOE=90°+25°=115°,
故选:C.
3.解:如图,连接BP,
∵菱形ABCD的周长是12cm,面积是6cm2,
∴AB=BC==3(cm),S△ABC==3(cm2),
∵S△ABC=S△ABP+S△BPC,
∴3=AB?PF+BC?PE,
∴3=×3×PE+×3×PF=(PE+PF),
∴PE+PF=2(cm),
故选:C.
4.解:如图,连接AC,
∵四边形ABCD是菱形,
∴AP=PC=CQ=AQ,AQ∥PC,AC⊥BD,
∴∠AQP=∠CPQ,
∴∠AQD=∠BPC,
∵AD∥BC,
∴∠ADQ=∠CBP,
在△ADQ和△CBP中,
,
∴△ADQ≌△CBP(AAS),
∴AD=BC,BP=DQ,故选项A不合题意;
又∵AD∥BC,
∴四边形ABCD是平行四边形,
∴AB=CD,AB∥CD,故选项C不合题意;
∵AC⊥BD,
∴平行四边形ABCD是菱形,
∴AB=AD,
∴∠ABD=∠ADB,故选项B不合题意;
故选:D.
5.解:延长AE,DC交于点G,过点F作FH⊥AD,交AD的延长线于H,
∵CD∥AB,
∴∠EAB=∠G,∠DAB=∠HDF=60°,
∵∠DFA=2∠EAB=∠G+∠FAG,
∴∠G=∠FAG,
∴AF=FG,
∵点E为BC的中点,
∴BE=CE,
在△CEG和△BEA中,
,
∴△CEG≌△BEA(AAS),
∴AB=CG=4,
设DF=x,
∴FC=4﹣x,
∴FG=8﹣x=AF,
∵HF⊥AD,∠HDF=60°,
∴∠DFH=30°,
∴DH=x,HF=x,
∵AF2=HF2+AH2,
∴(8﹣x)2=x2+(4+x)2,
∴x=,
∴CF=,
故选:D.
6.解:连接BD,交AC于点O,如图:
∵菱形ABCD的边长为10,点E、F分别是边CD、BC的中点,
∴AB∥CD,AB=BC=CD=DA=10,EF∥BD,
∵AC、BD是菱形的对角线,AC=16,
∴AC⊥BD,AO=CO=8,OB=OD,
又∵AB∥CD,EF∥BD,
∴DE∥BG,BD∥EG,
∴四边形BDEG是平行四边形,
∴BD=EG,
在△COD中,DO===6,
∴BD=2OD=12,
∴EG=BD=12,
故选:C.
7.解:∵四边形ABCD是菱形,
∴AB=BC=CD=DA,AB∥CD,OA=OC,OB=OD,AC⊥BD,
∴∠BAG=∠EDG,△ABO≌△BCO≌△CDO≌△AOD,
∵CD=DE,
∴AB=DE,
在△ABG和△DEG中,
,
∴△ABG≌△DEG(AAS),
∴AG=DG,
∴OG是△ACD的中位线,
∴OG=CD=AB,①正确;
∵AB∥CE,AB=DE,
∴四边形ABDE是平行四边形,
∵∠BCD=∠BAD=60°,
∴△ABD、△BCD是等边三角形,
∴AB=BD=AD,∠ODC=60°,
∴OD=AG,四边形ABDE是菱形,④正确;
∴AD⊥BE,
由菱形的性质得:△ABG≌△BDG≌△DEG,
在△ABG和△DCO中,
,
∴△ABG≌△DCO(SAS),
∴△ABO≌△BCO≌△CDO≌△AOD≌△ABG≌△BDG≌△DEG,②不正确;
∵OB=OD,
∴S△BOG=S△DOG,
∵四边形ABDE是菱形,
∴S△ABG=S△DGE,
∴四边形ODEG与四边形OBAG面积相等,故③正确;
故选:A.
8.解:过点A作AE⊥CD于E,AF⊥BC于F,连接AC,BD交于点O,
∵两条纸条宽度相同,
∴AE=AF.
∵AB∥CD,AD∥BC,
∴四边形ABCD是平行四边形.
∵S?ABCD=BC?AF=CD?AE.
又∵AE=AF.
∴BC=CD,
∴四边形ABCD是菱形,
∴AO=CO=1,BO=DO,AC⊥BD,
∴BO===2,
∴BD=4,
∴四边形ABCD的面积==4,
故选:A.
二.填空题(共8小题,每小题4分,共计32分)
9.解:如图,连接BD,交AC于点O,
∵四边形ABCD是菱形,周长为40,
∴AC⊥BD,AB=10,AO=CO=6,BO=DO,AD∥BC,
∴BO===8,
∴BD=16,
∵EG⊥AC,BD⊥AC,
∴GE∥BD,
又∵AD∥BC,
∴四边形EGBD是平行四边形,
∴BD=EG=16,
故答案为:16.
10.解:∵四边形ABCD是菱形,
∴AO=CO,AC⊥BD,
∵S菱形ABCD=12,
∴×BD×AC=12,
∴AC=6,
∵AE⊥BC,AO=CO,
∴OE=AC=3,
故答案为:3.
11.解:∵四边形ABCD是菱形,
∴AC⊥BD,OA=OC=AC=4,OB=OD=BD=3,
∴AB===5,
∴S菱形ABCD=AC?BD=AB?DH,
∴DH==,
故答案为:.
12.解:∵四边形ABCD是菱形,
∴∠C=∠BAD=120°,∠ABC=60°,∠ABD=ABC=30°,AB=AD,
∵AE=BE,
∴∠BAE=∠ABE=∠ADB=30°,
∴∠DAE=90°,
设AE=BE=xcm,则DE=(12﹣x)cm,
∴12﹣x=2x,
∴x=4,
∴DE=8cm,
故答案为:8.
13.解:∵四边形ABCD是菱形,
∴AC⊥BD,AO=CO,BO=DO=4,
∴BD=8,
∵S菱形ABCD=48=,
∴AC=12,
∵CE⊥AD,AO=CO,
∴OE=AC=6,
故答案为6.
14.解:如图,
在菱形ABCD中,∠ABC=80°,
∴∠ABD=∠ABC=40°,AD∥BC,
∴∠BAD=180°﹣∠ABC=100°,
∵△ABE是等腰三角形,
∴AE=BE,或AB=BE,
当AE=BE时,
∴∠ABE=∠BAE=40°,
∴∠DAE=100°﹣40°=60°;
当AB=BE时,∴∠BAE=∠AEB=(180°﹣40°)=70°,
∴∠DAE=100°﹣70°=30°,
综上所述,当△ABE是等腰三角形时,∠DAE=30°或60°,
故答案为:30°或60°.
15.解:过点C作CM⊥GB于M,CN⊥GD,交GD的延长线于N.
∵四边形ABCD为菱形,
∴AB=AD=CD=BC,
∵AB=BD,
∴AB=BD=AD=CD=BC,
∴△ABD为等边三角形,△BCD是等边三角形,
∴∠A=∠BDF=60°,∠ADC=120°,
在△ADE和△DBF中,
,
∴△ADE≌△DBF(SAS),
∴∠ADE=∠DBF,
∵∠FBC=60°+∠DBF,∠NDC=180°﹣(120°﹣∠ADE)=60°+∠ADE,
∴∠NDC=∠FBC,
在△CDN和△CBM中,
,
∴△CDN≌△CBM(AAS),
∴CM=CN,
在Rt△CBM与Rt△CDN中,
,
∴Rt△CBM≌Rt△CDN(HL),
∴S四边形BCDG=S四边形CMGN.S四边形CMGN=2S△CMG,
∵∠CGM=60°,
∴GM=CG=,CM=CG=,
∴S四边形BCDG=S四边形CMGN=2S△CMG=2×××=,
故答案为:.
16.解:∵四边形ABCD是菱形,
∴AB=AD=BC=CD,
∵∠A=60°,
∴△ABD是等边三角形,
∴S△ABD=×BD2=16,
∴菱形ABCD的面积=32,
∵EF是对边中位线,
∴AE=AD,BF=BC,
∴AE=BF,
且AE∥BF,
∴四边形AEFB是平行四边形,
∴?AEFB的面积=16,EF∥AB,
∵EG是邻边中位线,
∴S△EFG=S?AEFB=8,
故答案为8.
三.解答题(共7小题,每小题8分,共计56分)
17.解:(1)在△ABC和△DEF中,
∴△ABC≌△DEF(SAS),
∴BC=EF,∠ACB=∠DFE,
∴BC∥EF,
∴四边形BCEF是平行四边形;
(2)当时,四边形BCEF是菱形.
理由如下:
连接BE,交CF与点H,
∵AC=DF,
∴AC﹣FC=DF﹣FC,
即AF=CD,
若四边形BCEF是菱形时,
∴BE⊥CF,,EF=BC=3.
在Rt△ABC中,AB=4,BC=3,
∴.
∵,
即.
在Rt△BCH中,,BC=3,
∴.
∴,
∴,
∴当时,四边形BCEF是菱形.
18.证明:(1)∵四边形ABCD是平行四边形,
∴OA=OC,OB=OD.
∵E,O,F分别是对角线BD上的四等分点,
∴E,F分别为OB,OD的中点,
∵G是AD的中点,
∴GF为△AOD的中位线,
∴GF∥OA,GF=OA,
同理EH∥OC,EH=OC,
∴EH∥GF,EH=GF,
∴四边形GEHF是平行四边形;
(2)①AB⊥BD,理由如下:
如图,连接GH,
∵四边形ABCD是平行四边形,
∴AD=BC,AD∥BC,
∵点G、H分别是AD、BC的中点,
∴AG=AD,BH=BC,
∴AG=BH,
∴四边形AGHB是平行四边形,
∴AB∥HG,
∵四边形GEHF是菱形,
∴GH⊥EF,
∴AB⊥EF,即AB⊥BD;
②∵AB=2,BD=2AB,
∴BD=4,
∵点E、O、F分别是对角线BD上的四等分点,
∴EO=OF=1,
∴EF=2,
∵四边形AGHB是平行四边形,
∴GH=AB=2,
∵四边形GEHF是菱形,
∴四边形GEHF的面积=×EF×GH=×2×2=2.
19.解:(1)∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠DAE=∠AEB,
∵∠EAF=∠EAB,
∴∠BAE=∠BEA,
∴BA=BE,
∵BF⊥AE,
∴∠ABF=∠FBE,∠AFB=∠FBE,
∴∠ABF=∠AFB,
∴AB=AF,
∴AF=BE,
∵AF∥BE,
∴四边形ABEF是平行四边形,
∵AB=AF,
∴四边形ABEF是菱形.
(2)连接CF,
CE=1,CF=2,AB=,
∵AB=EF=,
CE2+CF2=EF2,
∴CF⊥BC,
∴菱形ABEF的面积=×2=.
20.(1)证明:∵四边形ABCD是菱形,
∴OA=AC,OB=OD=BD=3,AC⊥BD,
∴∠AOB=90°,
∴OA===4,
∴AC=2OA=8,
∵E、F分别是AB、AD的中点,
∴EF是△ABD的中位线,
∴EF=BD=4,
(2)四边形DEOF是菱形.理由如下:
∵四边形ABCD是菱形,
∴DA=DC,OA=OC,OB=OD,
∴O是AC,BD的中点,
∵E,F分别是菱形ABCD的边AD,CD的中点,
∴DE=DA,DF=DC,OE,OF分别是△ACD和△CDA的中位线,
∴DE=DF,OE∥FD,OF∥DE,
∴四边形DEOF平行四边形,
∵DE=DF,
∴四边形DEOF是菱形.
21.证明:(1)∵四边形ABCD是菱形,
∴AC⊥BD,DO=BO,
又∵DH⊥AB,
∴DO=BO=OH,∠BDH+∠DBH=90°=∠DBH+∠HAO,
∴∠OHD=∠ODH,∠BDH=∠HAO,
∴∠OHD=∠OAH;
(2)∵四边形ABCD是菱形,
∴AC⊥BD,DO=BO=3,AO=CO=4,
∴AB===5,
∵S△ADB=×BD×AO=×AB×DH,
∴6×4=5DH,
∴DH=,
∴BH===.
22.解:(1)AB=CG﹣CE,
理由如下:∵四边形ABCD是菱形,四边形AEFG是菱形,
∴AB=BC,AE=AG,
∵∠BAC=60°,
∴△ABC是等边三角形,
∴∠ABC=∠ACB=∠BAC=60°,AB=AC,
∴∠BAC=∠EAG=60°,
∴∠BAC+∠CAE=∠EAG+∠CAE.即∠BAE=∠CAG,
在△ABE和△ACG中,
,
∴△ABE≌△ACG(SAS),
∴BE=CG,
∵AB=BC=BE﹣CE,
∴AB=CG﹣CE;
(2)AB=CE﹣CG,
理由如下:理由如下:∵四边形ABCD是菱形,
∴AB=BC,
∵∠BAC=60°,
∴△ABC是等边三角形,
∴∠ABC=∠ACB=∠BAC=60°,AB=AC.
∴∠BAC=∠EAG=60°,
∴∠BAC﹣∠BAG=∠EAG﹣∠BAG,即∠BAE=∠CAG,
在△ABE和△ACG中,
,
∴△ABE≌△ACG(SAS),
∴BE=CG,
∵AB=BC=CE﹣BE,
∴AB=CE﹣CG;
23.证明:(1)∵四边形ABCD是平行四边形,
∴DC∥AB,
∴∠CDB=∠ABD,
∵BD平分∠ABC,
∴∠CBD=∠ABD,
∴∠CDB=∠CBD,
∴DC=BC,
∵四边形ABCD是平行四边形,
∴四边形ABCD是菱形;
(2)①∵四边形ABCD是菱形,
∴DC=DA,∠CDG=∠ADG,
在△ADG和△CDG中
,
∴△ADG≌△CDG(SAS),
∴AG=CG,
∵GF是EC的垂直平分线,
∴CG=EG,
∴AG=EG,
即△AGE是等腰三角形;
②连接AC交BD于O,
∵GC=GE,
∴∠GCE=∠GEC,
∵AG=CG=GE,
∴∠GCA=∠GAC,∠GAE=∠GEA,
∵∠CBA=60°,BC=AB,
∴∠CAB=∠ACB=60°,
∴∠GAC+∠GAE=60°,
∴∠GAC+∠GCA+∠GAE+∠GEA=120°,
∴∠AGC+∠AGE=240°,
∴∠CGE=120°,
∴∠GCE=30°,
∴CG=2GF,
∴AG=2GF,
∴=.
同步能力达标测评(附答案)
一.选择题(共8小题,每小题4分,共计32分)
1.如图,在平面直角坐标系xOy中,菱形ABCD的顶点D在x轴上,边BC在y轴上,若点A的坐标为(2,3),则C点的坐标为( )
A.(0,﹣2)
B.(0,﹣1.5)
C.(0,﹣1)
D.(﹣2,0)
2.如图,在菱形ABCD中,∠ABC=50°,对角线AC,BD交于点O,E为CD的中点,连接OE,则∠AOE的度数是( )
A.110°
B.112°
C.115°
D.120°
3.如图,AC是菱形ABCD的对角线,P是AC上一个动点,过点P分别作AB、BC的垂线,垂足分别是F和E.若菱形ABCD的周长是12cm,面积是6cm2,则PE+PF的值是( )
A.1.5
B.1
C.2
D.4
4.四边形ABCD中,AD∥BC,点P,Q是对角线BD上不同的两点,若四边形APCQ是菱形,则下列说法中不正确的是( )
A.BP=DQ
B.∠ABD=∠ADB
C.AB∥CD
D.∠ABP=∠BAP
5.如图四边形ABCD为菱形,点E为BC的中点,点F在CD上,若∠DAB=60°,∠DFA=2∠EAB,AD=4,则CF的长为( )
A.
B.
C.
D.
6.如图,菱形ABCD的边长为10,对角线AC=16,点E、F分别是边CD、BC的中点,连接EF并延长与AB的延长线相交于点G,则EG长为( )
A.13
B.10
C.12
D.5
7.如图,在菱形ABCD中,∠BAD=60°,AC与BD交于点O,E为CD延长线上的一点,且CD=DE,连接BE分别交AC、AD于点F、G,连接OG,则下列结论中一定成立的是( )
①OG=AB;②与△DEG全等的三角形共有5个;③四边形ODEG与四边形OBAG面积相等;④由点A、B、D、E构成的四边形是菱形.
A.①③④
B.①④
C.①②③
D.②③④
8.如图,两张等宽的纸条交叉叠放在一起,若重合部分构成的四边形ABCD中,AB=3,AC=2,则四边形ABCD的面积为( )
A.
B.
C.
D.5
二.填空题(共8小题,每小题4分,共计32分)
9.如图,菱形ABCD的周长为40,对角线AC=12.过AD的中点E作EG⊥AC交AB于点F,交CB的延长线于点G,则EG的长为
.
10.如图,菱形ABCD的对角线相交于点O,过点A作AE⊥CB交CB的延长线与点E,连接OE,若S菱形ABCD=12,BD=4,则OE的长为
.
11.如图,四边形ABCD是菱形,对角线AC=8,DB=6,DH⊥AB于点H,则DH的长为
.
12.如图,在菱形ABCD中,点E在对角线BD上,AE=BE,∠C=120°,若BD=12cm,则DE=
cm.
13.如图,菱形ABCD的对角线AC、BD相交于点O,过点C作CE⊥AD于点E,连接OE,若OB=4,S菱形ABCD=48,则OE的长为
.
14.在菱形ABCD中,∠ABC=80°,E是线段BD上一动点(不与点B、D重合),当△ABE是等腰三角形时,∠DAE的度数为
.
15.如图,在菱形ABCD中,AB=BD,点E、F分别在AB、AD上,且AE=DF,连接BF与DE交于点G,若CG=1,则S四边形BCDG=
.
16.我们定义:联结平行四边形一组对边中点的线段叫做“对边中位线”,联结平行四边形一组邻边中点的线段叫做“邻边中位线”.如图,在菱形ABCD中,∠A=60°,对角线BD=8,那么“对边中位线”EF与“邻边中位线”EG、FG所围成的△EFG的面积是
.
三.解答题(共7小题,每小题,8分,共计56分)
17.如图,点A,F,C,D在同一条直线上,点B,E分别在直线AD两侧,且AB=DE,∠A=∠D,AC=DF.
(1)求证:四边形BCEF是平行四边形,
(2)若∠ABC=90°,EF=3,AB=4,当CD为何值时,四边形BCEF是菱形.
18.已知:如图,在?ABCD中,对角线AC、BD相交于点O,点G、H分别是AD、BC的中点,点E、O、F分别是对角线BD上的四等分点,顺次连接G、E、H、F.
(1)求证:四边形GEHF是平行四边形;
(2)若四边形GEHF是菱形.
①线段AB和BD有何位置关系?请说明理由.
②若AB=2,BD=2AB时,求四边形GEHF的面积.
19.如图,在?ABCD中,AE平分∠BAD交BC于点E,过点B作BF⊥AE于点H,交AD于点F,连接EF.
(1)求证:四边形ABEF是菱形;
(2)连接CF,若CE=1,CF=2,,求菱形ABEF的面积.
20.如图,E,F分别是菱形ABCD的边AD,CD的中点,且AB=5,BD=6.
(1)求线段EF的长;
(2)探究四边形DEOF是什么特殊四边形?并对结论给予证明.
21.如图,四边形ABCD是菱形,对角线AC、BD相交于点O,DH⊥AB于H,连接OH.
(1)求证:∠OHD=∠OAH.
(2)若AC=8,BD=6,求BH.
22.已知AC是菱形ABCD的对角线,∠BAC=60°,点E是直线BC上的一个动点,连接AE,以AE为边作菱形AEFG,并且使∠EAG=60°,连接CG,当点E在线段BC上时,如图1,易证:AB=CG+CE.
(1)当点E在线段BC的延长线上时(如图2),猜想AB,CG,CE之间的关系并证明;
(2)当点E在线段CB的延长线上时(如图3),直接写出AB,CG,CE之间的关系.
23.如图1,已知平行四边形ABCD中,BD平分∠CBA.
(1)求证:平行四边形ABCD是菱形;
(2)如图2,E为边AB上一动点,连接CE,作CE的垂直平分线交CE于F,交DB于G,连接AG、EG,
①求证:△AGE为等腰三角形;
②若∠CBA=60°,求的值.
参考答案
一.选择题(共8小题,每小题4分,共计32分)
1.解:∵A(2,3),
∴OD=2,AD=3,
∵四边形ABCD是菱形,
∴CD=AD=3,
在Rt△ODC中,OC===1,
∴C(0,﹣1).
故选:C.
2.解:∵四边形ABCD是菱形,
∴AC⊥BD,∠CDO=∠ADC=∠ABC=25°,
∴∠DOC=90°,
∵点E是CD的中点,
∴OE=DE=CD,
∴∠DOE=∠CDO=25°,
∴∠AOE=∠AOD+∠DOE=90°+25°=115°,
故选:C.
3.解:如图,连接BP,
∵菱形ABCD的周长是12cm,面积是6cm2,
∴AB=BC==3(cm),S△ABC==3(cm2),
∵S△ABC=S△ABP+S△BPC,
∴3=AB?PF+BC?PE,
∴3=×3×PE+×3×PF=(PE+PF),
∴PE+PF=2(cm),
故选:C.
4.解:如图,连接AC,
∵四边形ABCD是菱形,
∴AP=PC=CQ=AQ,AQ∥PC,AC⊥BD,
∴∠AQP=∠CPQ,
∴∠AQD=∠BPC,
∵AD∥BC,
∴∠ADQ=∠CBP,
在△ADQ和△CBP中,
,
∴△ADQ≌△CBP(AAS),
∴AD=BC,BP=DQ,故选项A不合题意;
又∵AD∥BC,
∴四边形ABCD是平行四边形,
∴AB=CD,AB∥CD,故选项C不合题意;
∵AC⊥BD,
∴平行四边形ABCD是菱形,
∴AB=AD,
∴∠ABD=∠ADB,故选项B不合题意;
故选:D.
5.解:延长AE,DC交于点G,过点F作FH⊥AD,交AD的延长线于H,
∵CD∥AB,
∴∠EAB=∠G,∠DAB=∠HDF=60°,
∵∠DFA=2∠EAB=∠G+∠FAG,
∴∠G=∠FAG,
∴AF=FG,
∵点E为BC的中点,
∴BE=CE,
在△CEG和△BEA中,
,
∴△CEG≌△BEA(AAS),
∴AB=CG=4,
设DF=x,
∴FC=4﹣x,
∴FG=8﹣x=AF,
∵HF⊥AD,∠HDF=60°,
∴∠DFH=30°,
∴DH=x,HF=x,
∵AF2=HF2+AH2,
∴(8﹣x)2=x2+(4+x)2,
∴x=,
∴CF=,
故选:D.
6.解:连接BD,交AC于点O,如图:
∵菱形ABCD的边长为10,点E、F分别是边CD、BC的中点,
∴AB∥CD,AB=BC=CD=DA=10,EF∥BD,
∵AC、BD是菱形的对角线,AC=16,
∴AC⊥BD,AO=CO=8,OB=OD,
又∵AB∥CD,EF∥BD,
∴DE∥BG,BD∥EG,
∴四边形BDEG是平行四边形,
∴BD=EG,
在△COD中,DO===6,
∴BD=2OD=12,
∴EG=BD=12,
故选:C.
7.解:∵四边形ABCD是菱形,
∴AB=BC=CD=DA,AB∥CD,OA=OC,OB=OD,AC⊥BD,
∴∠BAG=∠EDG,△ABO≌△BCO≌△CDO≌△AOD,
∵CD=DE,
∴AB=DE,
在△ABG和△DEG中,
,
∴△ABG≌△DEG(AAS),
∴AG=DG,
∴OG是△ACD的中位线,
∴OG=CD=AB,①正确;
∵AB∥CE,AB=DE,
∴四边形ABDE是平行四边形,
∵∠BCD=∠BAD=60°,
∴△ABD、△BCD是等边三角形,
∴AB=BD=AD,∠ODC=60°,
∴OD=AG,四边形ABDE是菱形,④正确;
∴AD⊥BE,
由菱形的性质得:△ABG≌△BDG≌△DEG,
在△ABG和△DCO中,
,
∴△ABG≌△DCO(SAS),
∴△ABO≌△BCO≌△CDO≌△AOD≌△ABG≌△BDG≌△DEG,②不正确;
∵OB=OD,
∴S△BOG=S△DOG,
∵四边形ABDE是菱形,
∴S△ABG=S△DGE,
∴四边形ODEG与四边形OBAG面积相等,故③正确;
故选:A.
8.解:过点A作AE⊥CD于E,AF⊥BC于F,连接AC,BD交于点O,
∵两条纸条宽度相同,
∴AE=AF.
∵AB∥CD,AD∥BC,
∴四边形ABCD是平行四边形.
∵S?ABCD=BC?AF=CD?AE.
又∵AE=AF.
∴BC=CD,
∴四边形ABCD是菱形,
∴AO=CO=1,BO=DO,AC⊥BD,
∴BO===2,
∴BD=4,
∴四边形ABCD的面积==4,
故选:A.
二.填空题(共8小题,每小题4分,共计32分)
9.解:如图,连接BD,交AC于点O,
∵四边形ABCD是菱形,周长为40,
∴AC⊥BD,AB=10,AO=CO=6,BO=DO,AD∥BC,
∴BO===8,
∴BD=16,
∵EG⊥AC,BD⊥AC,
∴GE∥BD,
又∵AD∥BC,
∴四边形EGBD是平行四边形,
∴BD=EG=16,
故答案为:16.
10.解:∵四边形ABCD是菱形,
∴AO=CO,AC⊥BD,
∵S菱形ABCD=12,
∴×BD×AC=12,
∴AC=6,
∵AE⊥BC,AO=CO,
∴OE=AC=3,
故答案为:3.
11.解:∵四边形ABCD是菱形,
∴AC⊥BD,OA=OC=AC=4,OB=OD=BD=3,
∴AB===5,
∴S菱形ABCD=AC?BD=AB?DH,
∴DH==,
故答案为:.
12.解:∵四边形ABCD是菱形,
∴∠C=∠BAD=120°,∠ABC=60°,∠ABD=ABC=30°,AB=AD,
∵AE=BE,
∴∠BAE=∠ABE=∠ADB=30°,
∴∠DAE=90°,
设AE=BE=xcm,则DE=(12﹣x)cm,
∴12﹣x=2x,
∴x=4,
∴DE=8cm,
故答案为:8.
13.解:∵四边形ABCD是菱形,
∴AC⊥BD,AO=CO,BO=DO=4,
∴BD=8,
∵S菱形ABCD=48=,
∴AC=12,
∵CE⊥AD,AO=CO,
∴OE=AC=6,
故答案为6.
14.解:如图,
在菱形ABCD中,∠ABC=80°,
∴∠ABD=∠ABC=40°,AD∥BC,
∴∠BAD=180°﹣∠ABC=100°,
∵△ABE是等腰三角形,
∴AE=BE,或AB=BE,
当AE=BE时,
∴∠ABE=∠BAE=40°,
∴∠DAE=100°﹣40°=60°;
当AB=BE时,∴∠BAE=∠AEB=(180°﹣40°)=70°,
∴∠DAE=100°﹣70°=30°,
综上所述,当△ABE是等腰三角形时,∠DAE=30°或60°,
故答案为:30°或60°.
15.解:过点C作CM⊥GB于M,CN⊥GD,交GD的延长线于N.
∵四边形ABCD为菱形,
∴AB=AD=CD=BC,
∵AB=BD,
∴AB=BD=AD=CD=BC,
∴△ABD为等边三角形,△BCD是等边三角形,
∴∠A=∠BDF=60°,∠ADC=120°,
在△ADE和△DBF中,
,
∴△ADE≌△DBF(SAS),
∴∠ADE=∠DBF,
∵∠FBC=60°+∠DBF,∠NDC=180°﹣(120°﹣∠ADE)=60°+∠ADE,
∴∠NDC=∠FBC,
在△CDN和△CBM中,
,
∴△CDN≌△CBM(AAS),
∴CM=CN,
在Rt△CBM与Rt△CDN中,
,
∴Rt△CBM≌Rt△CDN(HL),
∴S四边形BCDG=S四边形CMGN.S四边形CMGN=2S△CMG,
∵∠CGM=60°,
∴GM=CG=,CM=CG=,
∴S四边形BCDG=S四边形CMGN=2S△CMG=2×××=,
故答案为:.
16.解:∵四边形ABCD是菱形,
∴AB=AD=BC=CD,
∵∠A=60°,
∴△ABD是等边三角形,
∴S△ABD=×BD2=16,
∴菱形ABCD的面积=32,
∵EF是对边中位线,
∴AE=AD,BF=BC,
∴AE=BF,
且AE∥BF,
∴四边形AEFB是平行四边形,
∴?AEFB的面积=16,EF∥AB,
∵EG是邻边中位线,
∴S△EFG=S?AEFB=8,
故答案为8.
三.解答题(共7小题,每小题8分,共计56分)
17.解:(1)在△ABC和△DEF中,
∴△ABC≌△DEF(SAS),
∴BC=EF,∠ACB=∠DFE,
∴BC∥EF,
∴四边形BCEF是平行四边形;
(2)当时,四边形BCEF是菱形.
理由如下:
连接BE,交CF与点H,
∵AC=DF,
∴AC﹣FC=DF﹣FC,
即AF=CD,
若四边形BCEF是菱形时,
∴BE⊥CF,,EF=BC=3.
在Rt△ABC中,AB=4,BC=3,
∴.
∵,
即.
在Rt△BCH中,,BC=3,
∴.
∴,
∴,
∴当时,四边形BCEF是菱形.
18.证明:(1)∵四边形ABCD是平行四边形,
∴OA=OC,OB=OD.
∵E,O,F分别是对角线BD上的四等分点,
∴E,F分别为OB,OD的中点,
∵G是AD的中点,
∴GF为△AOD的中位线,
∴GF∥OA,GF=OA,
同理EH∥OC,EH=OC,
∴EH∥GF,EH=GF,
∴四边形GEHF是平行四边形;
(2)①AB⊥BD,理由如下:
如图,连接GH,
∵四边形ABCD是平行四边形,
∴AD=BC,AD∥BC,
∵点G、H分别是AD、BC的中点,
∴AG=AD,BH=BC,
∴AG=BH,
∴四边形AGHB是平行四边形,
∴AB∥HG,
∵四边形GEHF是菱形,
∴GH⊥EF,
∴AB⊥EF,即AB⊥BD;
②∵AB=2,BD=2AB,
∴BD=4,
∵点E、O、F分别是对角线BD上的四等分点,
∴EO=OF=1,
∴EF=2,
∵四边形AGHB是平行四边形,
∴GH=AB=2,
∵四边形GEHF是菱形,
∴四边形GEHF的面积=×EF×GH=×2×2=2.
19.解:(1)∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠DAE=∠AEB,
∵∠EAF=∠EAB,
∴∠BAE=∠BEA,
∴BA=BE,
∵BF⊥AE,
∴∠ABF=∠FBE,∠AFB=∠FBE,
∴∠ABF=∠AFB,
∴AB=AF,
∴AF=BE,
∵AF∥BE,
∴四边形ABEF是平行四边形,
∵AB=AF,
∴四边形ABEF是菱形.
(2)连接CF,
CE=1,CF=2,AB=,
∵AB=EF=,
CE2+CF2=EF2,
∴CF⊥BC,
∴菱形ABEF的面积=×2=.
20.(1)证明:∵四边形ABCD是菱形,
∴OA=AC,OB=OD=BD=3,AC⊥BD,
∴∠AOB=90°,
∴OA===4,
∴AC=2OA=8,
∵E、F分别是AB、AD的中点,
∴EF是△ABD的中位线,
∴EF=BD=4,
(2)四边形DEOF是菱形.理由如下:
∵四边形ABCD是菱形,
∴DA=DC,OA=OC,OB=OD,
∴O是AC,BD的中点,
∵E,F分别是菱形ABCD的边AD,CD的中点,
∴DE=DA,DF=DC,OE,OF分别是△ACD和△CDA的中位线,
∴DE=DF,OE∥FD,OF∥DE,
∴四边形DEOF平行四边形,
∵DE=DF,
∴四边形DEOF是菱形.
21.证明:(1)∵四边形ABCD是菱形,
∴AC⊥BD,DO=BO,
又∵DH⊥AB,
∴DO=BO=OH,∠BDH+∠DBH=90°=∠DBH+∠HAO,
∴∠OHD=∠ODH,∠BDH=∠HAO,
∴∠OHD=∠OAH;
(2)∵四边形ABCD是菱形,
∴AC⊥BD,DO=BO=3,AO=CO=4,
∴AB===5,
∵S△ADB=×BD×AO=×AB×DH,
∴6×4=5DH,
∴DH=,
∴BH===.
22.解:(1)AB=CG﹣CE,
理由如下:∵四边形ABCD是菱形,四边形AEFG是菱形,
∴AB=BC,AE=AG,
∵∠BAC=60°,
∴△ABC是等边三角形,
∴∠ABC=∠ACB=∠BAC=60°,AB=AC,
∴∠BAC=∠EAG=60°,
∴∠BAC+∠CAE=∠EAG+∠CAE.即∠BAE=∠CAG,
在△ABE和△ACG中,
,
∴△ABE≌△ACG(SAS),
∴BE=CG,
∵AB=BC=BE﹣CE,
∴AB=CG﹣CE;
(2)AB=CE﹣CG,
理由如下:理由如下:∵四边形ABCD是菱形,
∴AB=BC,
∵∠BAC=60°,
∴△ABC是等边三角形,
∴∠ABC=∠ACB=∠BAC=60°,AB=AC.
∴∠BAC=∠EAG=60°,
∴∠BAC﹣∠BAG=∠EAG﹣∠BAG,即∠BAE=∠CAG,
在△ABE和△ACG中,
,
∴△ABE≌△ACG(SAS),
∴BE=CG,
∵AB=BC=CE﹣BE,
∴AB=CE﹣CG;
23.证明:(1)∵四边形ABCD是平行四边形,
∴DC∥AB,
∴∠CDB=∠ABD,
∵BD平分∠ABC,
∴∠CBD=∠ABD,
∴∠CDB=∠CBD,
∴DC=BC,
∵四边形ABCD是平行四边形,
∴四边形ABCD是菱形;
(2)①∵四边形ABCD是菱形,
∴DC=DA,∠CDG=∠ADG,
在△ADG和△CDG中
,
∴△ADG≌△CDG(SAS),
∴AG=CG,
∵GF是EC的垂直平分线,
∴CG=EG,
∴AG=EG,
即△AGE是等腰三角形;
②连接AC交BD于O,
∵GC=GE,
∴∠GCE=∠GEC,
∵AG=CG=GE,
∴∠GCA=∠GAC,∠GAE=∠GEA,
∵∠CBA=60°,BC=AB,
∴∠CAB=∠ACB=60°,
∴∠GAC+∠GAE=60°,
∴∠GAC+∠GCA+∠GAE+∠GEA=120°,
∴∠AGC+∠AGE=240°,
∴∠CGE=120°,
∴∠GCE=30°,
∴CG=2GF,
∴AG=2GF,
∴=.
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
