2.5.5切线长定理-2021-2022学年苏科版九年级数学上册培优训练(Word版 含答案)
文档属性
| 名称 | 2.5.5切线长定理-2021-2022学年苏科版九年级数学上册培优训练(Word版 含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 2.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-18 15:36:10 | ||
图片预览


文档简介
2.5.5切线长定理
-2021-2022学年苏科版九年级数学上册
培优训练
一、选择题
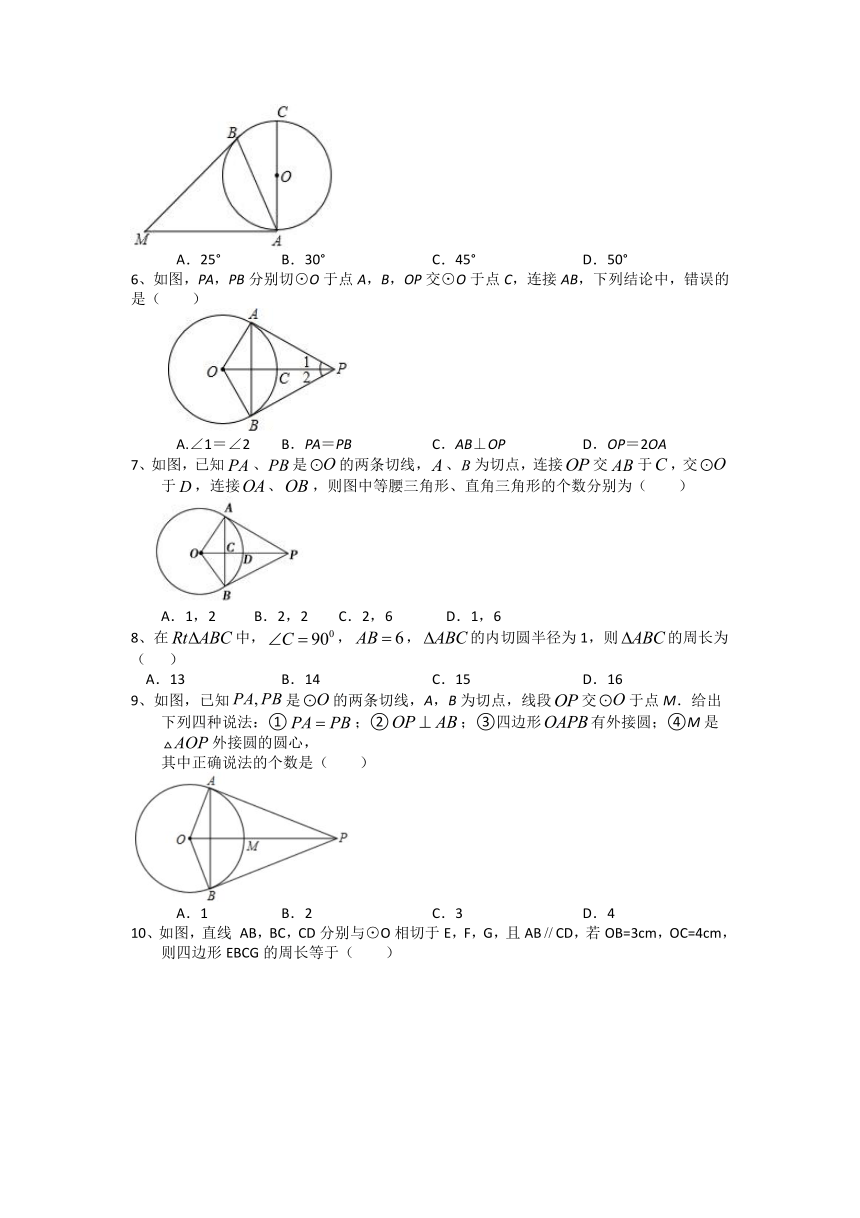
1、如图,△ABC的内切圆⊙O与AB,BC,CA分别相切于点D,E,F,且AD=2,BC=5,
则△ABC的周长为( )
A.16
B.14
C.12
D.10
2、如图,AB是⊙O的直径,点C为⊙O外一点,CA、CD是⊙O的切线,A、D为切点,连接BD、AD.若∠ACD=48°,则∠DBA的大小是( )
A.32°
B.48°
C.60°
D.66°
3、如图,四边形ABCD是⊙O的外切四边形,且AB=10,CD=12,则四边形ABCD的周长为( )
A.44
B.42
C.46
D.47
4、如图,
PA,PB,DE分别切⊙O于点A,B,C,过C的切线分别交PA,PB于点E,D,若△PDE的周长为8,OP=5,则⊙O的半径为( )
A.2
B.3
C.4
D.不能确定
5、如图,⊙O中,AC为直径,MA,MB分别切⊙O于点A,B,∠BAC=25°,则∠AMB的大小为( )
A.25°
B.30°
C.45°
D.50°
6、如图,PA,PB分别切⊙O于点A,B,OP交⊙O于点C,连接AB,下列结论中,错误的是( )
A.∠1=∠2
B.PA=PB
C.AB⊥OP
D.OP=2OA
7、如图,已知、是的两条切线,、为切点,连接交于,交于,连接、,则图中等腰三角形、直角三角形的个数分别为(
)
A.1,2
B.2,2
C.2,6
D.1,6
8、在中,,,的内切圆半径为1,则的周长为(
)
A.13
B.14
C.15
D.16
9、如图,已知是的两条切线,A,B为切点,线段交于点M.给出下列四种说法:①;②;③四边形有外接圆;④M是外接圆的圆心,
其中正确说法的个数是(
)
A.1
B.2
C.3
D.4
10、如图,直线
AB,BC,CD分别与⊙O相切于E,F,G,且ABCD,若OB=3cm,OC=4cm,则四边形EBCG的周长等于( )
A.5cm
B.10cm
C.cm
D.cm
二、填空题
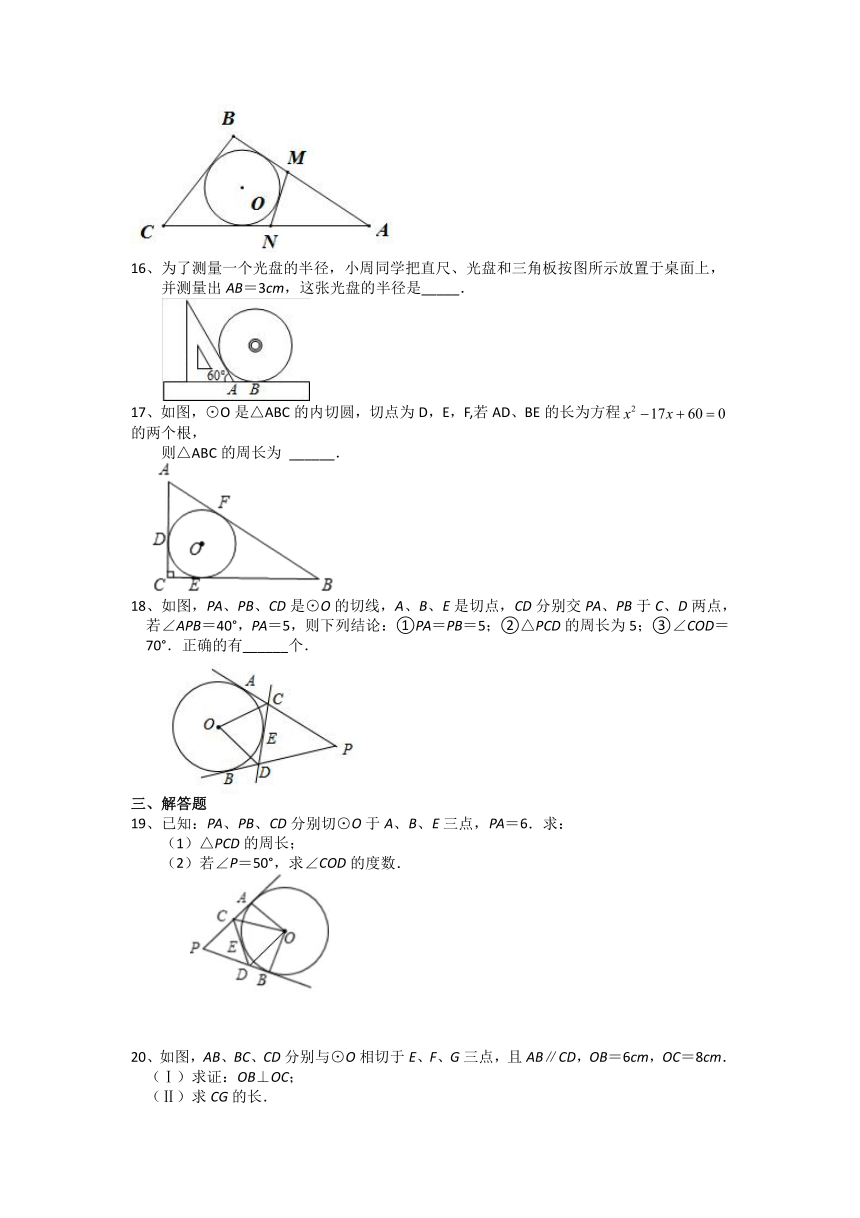
11、如图,是的切线,为切点,连接.若,则=__________.
12、如图:PA、PB切⊙O于A、B,过点C的切线交PA、PB于D、E,PA=8cm,则△PDE的周长为____cm.
13、如图,⊙O切△ABC的BC于D,切AB、AC的延长线于E、F,△ABC的周长为18,则AE=____.
14、如图,AB,AC,BD是⊙O的切线,P,C,D为切点.若AB=5
cm,AC=3
cm,则BD的长为____
cm.
15、如图,△ABC周长为20cm,BC=6cm,圆O是△ABC的内切圆,圆O的切线MN与AB、CA相交于点M、N,则△AMN的周长为________cm.
16、为了测量一个光盘的半径,小周同学把直尺、光盘和三角板按图所示放置于桌面上,并测量出AB=3cm,这张光盘的半径是_____.
17、如图,⊙O是△ABC的内切圆,切点为D,E,F,若AD、BE的长为方程的两个根,
则△ABC的周长为
______.
18、如图,PA、PB、CD是⊙O的切线,A、B、E是切点,CD分别交PA、PB于C、D两点,若∠APB=40°,PA=5,则下列结论:①PA=PB=5;②△PCD的周长为5;③∠COD=70°.正确的有______个.
三、解答题
19、已知:PA、PB、CD分别切⊙O于A、B、E三点,PA=6.求:
(1)△PCD的周长;
(2)若∠P=50°,求∠COD的度数.
20、如图,AB、BC、CD分别与⊙O相切于E、F、G三点,且AB∥CD,OB=6cm,OC=8cm.
(Ⅰ)求证:OB⊥OC;
(Ⅱ)求CG的长.
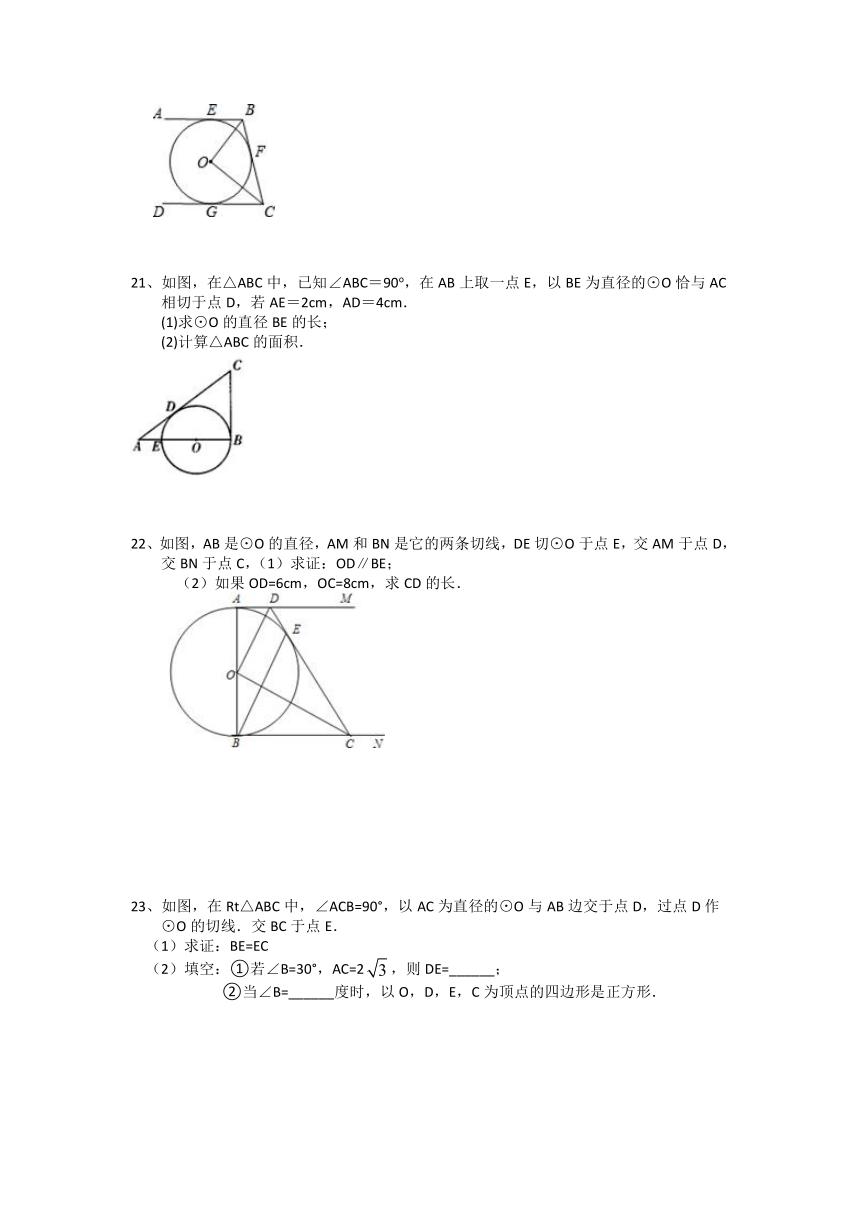
21、如图,在△ABC中,已知∠ABC=90o,在AB上取一点E,以BE为直径的⊙O恰与AC相切于点D,若AE=2cm,AD=4cm.
(1)求⊙O的直径BE的长;
(2)计算△ABC的面积.
22、如图,AB是⊙O的直径,AM和BN是它的两条切线,DE切⊙O于点E,交AM于点D,交BN于点C,(1)求证:OD∥BE;
(2)如果OD=6cm,OC=8cm,求CD的长.
23、如图,在Rt△ABC中,∠ACB=90°,以AC为直径的⊙O与AB边交于点D,过点D作⊙O的切线.交BC于点E.
(1)求证:BE=EC
(2)填空:①若∠B=30°,AC=2,则DE=______;
②当∠B=______度时,以O,D,E,C为顶点的四边形是正方形.
24、如图,四边形为矩形,以为直径作,过点作与相切于点,连接交于点,连接.
(1)求证:四边形为平行四边形;
(2)若点为的中点,,求的长.
2.5.5切线长定理
-2021-2022学年苏科版九年级数学上册
培优训练(有答案)
一、选择题
1、如图,△ABC的内切圆⊙O与AB,BC,CA分别相切于点D,E,F,且AD=2,BC=5,
则△ABC的周长为( )
A.16
B.14
C.12
D.10
【分析】根据切线长定理进行求解即可.
【详解】∵△ABC的内切圆⊙O与AB,BC,CA分别相切于点D,E,F,
∴AF=AD=2,BD=BE,CE=CF,
∵BE+CE=BC=5,∴BD+CF=BC=5,
∴△ABC的周长=2+2+5+5=14,
故选B.
2、如图,AB是⊙O的直径,点C为⊙O外一点,CA、CD是⊙O的切线,A、D为切点,连接BD、AD.若∠ACD=48°,则∠DBA的大小是( )
A.32°
B.48°
C.60°
D.66°
【分析】根据切线长定理可知CA=CD,求出∠CAD,再证明∠DBA=∠CAD即可解决问题.
【详解】解:∵CA、CD是⊙O的切线,∴CA=CD,
∵∠ACD=48°,∴∠CAD=∠CDA=66°,
∵CA⊥AB,AB是直径,∴∠ADB=∠CAB=90°,
∴∠DBA+∠DAB=90°,∠CAD+∠DAB=90°,∴∠DBA=∠CAD=66°,
故选D.
3、如图,四边形ABCD是⊙O的外切四边形,且AB=10,CD=12,则四边形ABCD的周长为( )
A.44
B.42
C.46
D.47
【答案】A
【分析】根据圆的切线的性质求解即可.
【详解】解:∵四边形ABCD是⊙O的外切四边形,
∴AD+BC=AB+CD=22,
∴四边形ABCD的周长=AD+BC+AB+CD=44,
故选:A.
4、如图,
PA,PB,DE分别切⊙O于点A,B,C,过C的切线分别交PA,PB于点E,D,若△PDE的周长为8,OP=5,则⊙O的半径为( )
A.2
B.3
C.4
D.不能确定
【答案】B
【分析】根据切线长定理得BD=CD,CE=AE,PA=PB,由△PDE的周长为8得到AP=BP=4,连接AO,利用勾股定理即可求出AO,即可求解.
【详解】连接OA.
∵PA、PB、DE分别切⊙O于A、B、C点,
∴BD=CD,CE=AE,PA=PB,OA⊥AP.
∴△PDE的周长为2AP=8,
∴AP=4
在直角三角形OAP中,根据勾股定理,得AO==3,
∴⊙O的半径为3.
故选B.
5、如图,⊙O中,AC为直径,MA,MB分别切⊙O于点A,B,∠BAC=25°,则∠AMB的大小为( )
A.25°
B.30°
C.45°
D.50°
【解析】
【分析】由AM与圆O相切,根据切线的性质得到AM垂直于AC,可得出∠MAC为直角,再由∠BAC的度数,用∠MAC﹣∠BAC求出∠MAB的度数,又MA,MB为圆O的切线,根据切线长定理得到MA=MB,利用等边对等角可得出∠MAB=∠MBA,由底角的度数,利用三角形的内角和定理即可求出∠AMB的度数.
【详解】解:∵MA切⊙O于点A,AC为直径,∴∠MAC=90°,
又∠BAC=25°,∴∠MAB=∠MAC﹣∠BAC=65°,
∵MA、MB分别切⊙O于点A、B,∴MA=MB,∴∠MAB=∠MBA=65°,
∴∠AMB=180°﹣(∠MAB+∠MBA)=50°,
故选:D.
6、如图,PA,PB分别切⊙O于点A,B,OP交⊙O于点C,连接AB,下列结论中,错误的是( )
A.∠1=∠2
B.PA=PB
C.AB⊥OP
D.OP=2OA
【答案】D
【分析】利用切线长定理、等腰三角形的性质即可得出.
【详解】由切线长定理可得:∠1=∠2,PA=PB,从而AB⊥OP.
因此A.B.C都正确.
无法得出AB=PA=PB,可知:D是错误的.
综上可知:只有D是错误的.
故选D.
7、如图,已知、是的两条切线,、为切点,连接交于,交于,连接、,则图中等腰三角形、直角三角形的个数分别为(
)
A.1,2
B.2,2
C.2,6
D.1,6
【答案】C
【分析】根据切线长定理及半径相等得,△APB为等腰三角形,△AOB为等腰三角形,共两个;
根据切线长定理和等腰三角形三线合一的性质,直角三角形有:△AOC,△AOP,△APC,△OBC,△OBP,△CBP,共6个.
【详解】解:因为OA、OB为圆O的半径,所以OA=OB,所以△AOB为等腰三角形,
根据切线长定理,PA=PB,故△APB为等腰三角形,共2个,
根据切线长定理,PA=PB,∠APC=∠BPC,PC=PC,所以△PAC≌△PBC,
故AB⊥PE,根据切线的性质定理∠OAP=∠OBP=90°,
所以直角三角形有:△AOC,△AOP,△APC,△OBC,△OBP,△CBP,共6个.
故选:C.
8、在中,,,的内切圆半径为1,则的周长为(
)
A.13
B.14
C.15
D.16
【分析】根据直角三角形的内切圆的半径等于两条直角边的和与斜边的差的一半,即可求得两条直角边的和,从而求得其周长.
【详解】
解:根据直角三角形的内切圆的半径公式,得,
.
则三角形的周长.
故选B.
9、如图,已知是的两条切线,A,B为切点,线段交于点M.给出下列四种说法:①;②;③四边形有外接圆;④M是外接圆的圆心,
其中正确说法的个数是(
)
A.1
B.2
C.3
D.4
【答案】C
【分析】由切线长定理判断①,结合等腰三角形的性质判断②,利用切线的性质与直角三角形的斜边上的中线等于斜边的一半,判断③,利用反证法判断④.
【详解】解:如图,
是的两条切线,
故①正确,
故②正确,
是的两条切线,
取的中点,连接,则
所以:以为圆心,为半径作圆,则共圆,故③正确,
若M是外接圆的圆心,
与题干提供的条件不符,故④错误,
综上:正确的说法是个,
故选C.
10、如图,直线
AB,BC,CD分别与⊙O相切于E,F,G,且ABCD,若OB=3cm,OC=4cm,则四边形EBCG的周长等于( )
A.5cm
B.10cm
C.cm
D.cm
【答案】C
【分析】连接OF,利用切线性质和切线长定理可证明BE=BF,CG=CF,∠OBE=∠OBF,∠OCG=∠OCF,OF⊥BC,再根据平行线的性质证得∠BOC=90°,进而由勾股定理求得BC长,根据三角形的面积公式求得OF,进而可求得四边形的周长.
【详解】解:连接OF,
∵直线
AB,BC,CD分别与⊙O相切于E,F,G,
∴BE=BF,CG=CF,∠OBE=∠OBF,∠OCG=∠OCF,OF⊥BC,
∵AB∥CD,∴∠ABC+∠DCB=180°,
∴∠OBF+∠OCF=90°,即∠BOC=90°,
∴在Rt△BOC中,OB=3cm,OC=4cm,由勾股定理得:
=5,
由得:OF=
cm,
∴OE=OG=OF=
cm,
∴四边形EBCG的周长为BE+BC+CG+EG=2OE+2BC=2×+2×5=cm,
故选:C.
二、填空题
11、如图,是的切线,为切点,连接.若,则=__________.
【分析】根据切线长定理即可得出AB=AC,然后根据等边对等角和三角形的内角和定理即可求出结论.
【详解】解:∵是的切线,∴AB=AC
∴∠ABC=∠ACB=(180°-∠A)=65°
故答案为:65°.
12、如图:PA、PB切⊙O于A、B,过点C的切线交PA、PB于D、E,PA=8cm,则△PDE的周长为____cm.
【分析】根据切线长定理,即可得到PA=PB,CD=AD,CE=BE,从而求得三角形的周长.
【详解】解:∵PA、PB切⊙O于A、B,DE切⊙O于C,
∴PA=PB=8,CD=AD,CE=BE;
∴△PDE的周长=PD+PE+CD+CE=2PA=16(cm).
故填:16.
13、如图,⊙O切△ABC的BC于D,切AB、AC的延长线于E、F,△ABC的周长为18,则AE=____.
【答案】9.
【分析】根据切线的性质得出BE=BD,DC=CF,进而解答即可.
【详解】解:∵⊙O切△ABC的BC于D,切AB、AC的延长线于E、F,
∴BE=BD,DC=CF,AF=AE,
∵△ABC的周长为18,
即AC+BC+AB=AB+DB+DC+AC=AB+BE+AC+CF=18,
∴AE+AF=18,∴AE=9,
故答案为:9.
14、如图,AB,AC,BD是⊙O的切线,P,C,D为切点.若AB=5
cm,AC=3
cm,则BD的长为____
cm.
【答案】2
【分析】由于AB、AC、BD是⊙O的切线,则AC=AP,BP=BD,求出BP的长即可求出BD的长.
【详解】∵AC、AP为⊙O的切线,∴AC=AP,
∵BP、BD为⊙O的切线,∴BP=BD,
∴BD=PB=AB-AP=5-3=2.
故答案是:2.
15、如图,△ABC周长为20cm,BC=6cm,圆O是△ABC的内切圆,圆O的切线MN与AB、CA相交于点M、N,则△AMN的周长为________cm.
【分析】先作出辅助线,连接切点,利用内切圆的性质得到BE=BF,CE=CG,ME=MH,NG=NH,再利用等量代换即可解题.
【详解】解:∵圆O是△ABC的内切圆,MN是圆O的切线,
如下图,连接各切点,有切线长定理易得,BE=BF,CE=CG,ME=MH,NG=NH,
∵△ABC周长为20cm,
BC=6cm,
∴BC=CE+BE=CG+BF=6cm,
∴△AMN的周长=AM+AN+MN=AM+AN+FM+GN=AF+AG,
又∵AF+AG=AB+AC-(BF+CG)=20-6-6=8cm
故答案是8
16、为了测量一个光盘的半径,小周同学把直尺、光盘和三角板按图所示放置于桌面上,并测量出AB=3cm,这张光盘的半径是_____.
【分析】连接OA,根据题意求出∠OAB=60°,再根据直角三角形的性质和勾股定理求得OB,从而得出光盘的直径.
【详解】如图,作OB⊥AB,连接OA,
∵∠CAD=60°,∴∠CAB=120°,
∵AB和AC与⊙O相切,∴∠OAB=∠OAC,∴∠OAB=∠CAB=60°
∵AB=3cm,∴OA=6cm,
∴由勾股定理得3cm,∴光盘的半径是3cm.
故答案为:3cm.
17、如图,⊙O是△ABC的内切圆,切点为D,E,F,若AD、BE的长为方程的两个根,
则△ABC的周长为
______.
【答案】40;
【解析】如图;解方程,得:x=12,x=5,
∴AD=AF=5,BF=BE=12;AB=17,
设CE=CD=x,则AC=5+x,BC=12+x;
由勾股定理,得:AB2=AC2+BC2,即172=(5+x)2+(12+x)2,
解得:x=3(负值舍去),
∴AC=8,BC=15;
因此△ABC的周长=AC+BC+AB=8+15+17=40,.
故答案为:40.
18、如图,PA、PB、CD是⊙O的切线,A、B、E是切点,CD分别交PA、PB于C、D两点,若∠APB=40°,PA=5,则下列结论:①PA=PB=5;②△PCD的周长为5;③∠COD=70°.正确的有______个.
【分析】根据切线长定理,可判断①正确;将的周长转化为,可判断②错误;连接、、,求出,再由,可判断③正确.
【详解】解:、是的切线,,故①正确;
、、是的切线,,,
的周长,故②错误;
连接、、,,
,故③正确.
综上可得①③正确,共2个.
三、解答题
19、已知:PA、PB、CD分别切⊙O于A、B、E三点,PA=6.求:
(1)△PCD的周长;
(2)若∠P=50°,求∠COD的度数.
【答案】(1)12;(2)
65°.
【解析】
【分析】(1)根据切线长定理,即可得到PA=PB,ED=AD,CE=BC,从而求得三角形的周长=2PA;
(2)连接OE,根据切线的性质得出∠P+∠AOB=180°,由切线长定理得∠COD=
∠AOB,即可得出结果.
解:(1)∵PA、PB切⊙O于A、B,CD切⊙O于E,
∴PA=PB=6,ED=AD,CE=BC;
∴△PCD的周长=PD+DE+PC+CE=2PA=12;
(2)连接OE,如图所示:
由切线的性质得,OA⊥PA,OB⊥PB,OE⊥CD,
∴∠OAC=∠OEC=∠OED=∠OBD=90°,
∴∠AOB+∠P=180°,∴∠AOB=180°﹣∠P=130°,
由切线长定理得:∠AOC=∠EOC,∠EOD=∠BOD,
∴∠COD=∠AOB=×130°=65°.
20、如图,AB、BC、CD分别与⊙O相切于E、F、G三点,且AB∥CD,OB=6cm,OC=8cm.
(Ⅰ)求证:OB⊥OC;
(Ⅱ)求CG的长.
【答案】(Ⅰ)证明见解析
(Ⅱ)6.4cm
【分析】(Ⅰ)根据切线的性质得到OB平分∠EBF,OC平分∠GCF,OF⊥BC,再根据平行线的性质得∠GCF+∠EBF=180°,则有∠OBC+∠OCB=90°,即∠BOC=90°;
(Ⅱ)由勾股定理可求得BC的长,进而由切线长定理即可得到CG的长.
【详解】解:(Ⅰ)连接OF;根据切线长定理得:BE=BF,CF=CG,∠OBF=∠OBE,∠OCF=∠OCG;
∵AB∥CD,∴∠ABC+∠BCD=180°,∴∠OBF+∠OCF=90°,
∴∠BOC=90°,∴OB⊥OC;
(Ⅱ)由(Ⅰ)知,∠BOC=90°.
∵OB=6cm,OC=8cm,
∴由勾股定理得到:BC==10cm,
∴
即
,
∴OF=4.8cm.
∴
=6.4cm,
∵CF、CG分别与⊙O相切于F、G,∴CG=CF=6.4cm.
21、如图,在△ABC中,已知∠ABC=90o,在AB上取一点E,以BE为直径的⊙O恰与AC相切于点D,若AE=2cm,AD=4cm.
(1)求⊙O的直径BE的长;
(2)计算△ABC的面积.
【答案】(1)BE=6;(2)
S△ABC=24..
【分析】(1)连接OD,由切线的性质得OD⊥AC,,在Rt△ODA中运用勾股定理可以求出半径OD,即可求得直径BE的长;
(2)由切线长定理知,CD=BC,在Rt△ABC中运用勾股定理可以求出BC,则可由直角三角形的面积公式求得△ABC的面积.
【详解】(1)连接OD,∴OD⊥AC∴△ODA是直角三角形
设半径为r,
∴AO=r+2,
∴,
解之得:r=3,
∴BE=6
(2)∵∠ABC=900,∴OB⊥BC,
∴BC是⊙O的切线
∵CD切⊙O于D,∴CB=CD
令CB=x,
∴AC=x+4,
CB=x,AB=8
∵,
∴x=6.,
∴S△ABC=24(cm2).
故答案为:(1)BE=6;(2)
S△ABC=24
22、如图,AB是⊙O的直径,AM和BN是它的两条切线,DE切⊙O于点E,交AM于点D,交BN于点C,(1)求证:OD∥BE;
(2)如果OD=6cm,OC=8cm,求CD的长.
【解析】
解:(1)证明:连接OE,
∵AM、DE是⊙O的切线,OA、OE是⊙O的半径,
∴∠ADO=∠EDO,
∠DAO=∠DEO=90°.∴∠AOD=∠EOD=∠AOE.
∵∠ABE=∠AOE,∴∠AOD=∠ABE.∴OD∥BE.
(2)由(1)得:∠AOD=∠EOD=∠AOE,
同理,有:∠BOC=∠EOC=∠BOE.
∴∠AOD+∠EOD+∠BOC+∠EOC=180°.∴∠EOD+∠EOC=90°.
∴△DOC是直角三角形.
∵OD=6cm,OC=8cm,
∴(cm)
.
23、如图,在Rt△ABC中,∠ACB=90°,以AC为直径的⊙O与AB边交于点D,过点D作⊙O的切线.交BC于点E.
(1)求证:BE=EC
(2)填空:①若∠B=30°,AC=2,则DE=______;
②当∠B=______度时,以O,D,E,C为顶点的四边形是正方形.
【答案】(1)见解析;(2)①3;②45.
【分析】(1)证出EC为⊙O的切线;由切线长定理得出EC=ED,再求得EB=ED,即可得出结论;
(2)①由含30°角的直角三角形的性质得出AB,由勾股定理求出BC,再由直角三角形斜边上的中线性质即可得出DE;
②由等腰三角形的性质,得到∠ODA=∠A=45°,于是∠DOC=90°然后根据有一组邻边相等的矩形是正方形,即可得到结论.
【详解】(1)证明:连接DO.
∵∠ACB=90°,AC为直径,∴EC为⊙O的切线;
又∵ED也为⊙O的切线,∴EC=ED,
又∵∠EDO=90°,∴∠BDE+∠ADO=90°,∴∠BDE+∠A=90°
又∵∠B+∠A=90°,∴∠BDE=∠B,∴BE=ED,∴BE=EC;
(2)解:①∵∠ACB=90°,∠B=30°,AC=2,∴AB=2AC=4,∴BC==6,
∵AC为直径,∴∠BDC=∠ADC=90°,
由(1)得:BE=EC,∴DE=BC=3,
故答案为3;
②当∠B=45°时,四边形ODEC是正方形,理由如下:
∵∠ACB=90°,∴∠A=45°,
∵OA=OD,∴∠ADO=45°,∴∠AOD=90°,∴∠DOC=90°,
∵∠ODE=90°,∴四边形DECO是矩形,
∵OD=OC,∴矩形DECO是正方形.
故答案为45.
24、如图,四边形为矩形,以为直径作,过点作与相切于点,连接交于点,连接.
(1)求证:四边形为平行四边形;
(2)若点为的中点,,求的长.
【答案】(1)证明见解析;(2)DC=.
【分析】(1)如图,连接DF、OF,DF交于G,根据AD为直径可得∠AFD=90°,根据切线性质可得∠OFC=90°,根据矩形的性质可得∠ADC=90°,OA//CE,可得DC是切线,根据切线长定理可得CF=DC,由OD=OF可得OC是线段DF的垂直平分线,可得∠OGD=90°,即可证明OC//AE,可得四边形AOCE是平行四边形;
(2)如图,连接OE、OF,由AD=2可得OA=OF=1,由平行四边形的性质可得OA=BE,进而可证明四边形AOEB是矩形,可得∠AOE=90°,OE=AB=CD,根据直角三角形斜边中线的性质可得AE的长,利用勾股定理求出OE的长即可得答案.
【详解】(1)如图,连接DF、OF,DF交于G,
∵AD为直径,∴∠AFD=90°,
∵与相切于点,∴∠OFC=90°,
∵四边形为矩形,∴∠ADC=∠DAB=90°,OA//CE,∴DC是切线,∴DC=CF,
∵OD=OF,∴OC是线段DF的垂直平分线,∴∠OGD=90°,∴OC//AE,
∴四边形AOCE是平行四边形.
(2)如图,连接OE、OF,
∵AD=2,OA=OD,∴OF=OA=1,
∵四边形AOCE是平行四边形,∴OA=CE,
∵AD=BC,∴OA=BE,
∵OA//BE,∴四边形AOEB是平行四边形,
∵∠DAB=90°,∴四边形AOEB是矩形,∴∠AOE=90°,OE=AB=DC,
∵F为AE中点,∴AE=2OF=2,∴DC=OE===.
-2021-2022学年苏科版九年级数学上册
培优训练
一、选择题
1、如图,△ABC的内切圆⊙O与AB,BC,CA分别相切于点D,E,F,且AD=2,BC=5,
则△ABC的周长为( )
A.16
B.14
C.12
D.10
2、如图,AB是⊙O的直径,点C为⊙O外一点,CA、CD是⊙O的切线,A、D为切点,连接BD、AD.若∠ACD=48°,则∠DBA的大小是( )
A.32°
B.48°
C.60°
D.66°
3、如图,四边形ABCD是⊙O的外切四边形,且AB=10,CD=12,则四边形ABCD的周长为( )
A.44
B.42
C.46
D.47
4、如图,
PA,PB,DE分别切⊙O于点A,B,C,过C的切线分别交PA,PB于点E,D,若△PDE的周长为8,OP=5,则⊙O的半径为( )
A.2
B.3
C.4
D.不能确定
5、如图,⊙O中,AC为直径,MA,MB分别切⊙O于点A,B,∠BAC=25°,则∠AMB的大小为( )
A.25°
B.30°
C.45°
D.50°
6、如图,PA,PB分别切⊙O于点A,B,OP交⊙O于点C,连接AB,下列结论中,错误的是( )
A.∠1=∠2
B.PA=PB
C.AB⊥OP
D.OP=2OA
7、如图,已知、是的两条切线,、为切点,连接交于,交于,连接、,则图中等腰三角形、直角三角形的个数分别为(
)
A.1,2
B.2,2
C.2,6
D.1,6
8、在中,,,的内切圆半径为1,则的周长为(
)
A.13
B.14
C.15
D.16
9、如图,已知是的两条切线,A,B为切点,线段交于点M.给出下列四种说法:①;②;③四边形有外接圆;④M是外接圆的圆心,
其中正确说法的个数是(
)
A.1
B.2
C.3
D.4
10、如图,直线
AB,BC,CD分别与⊙O相切于E,F,G,且ABCD,若OB=3cm,OC=4cm,则四边形EBCG的周长等于( )
A.5cm
B.10cm
C.cm
D.cm
二、填空题
11、如图,是的切线,为切点,连接.若,则=__________.
12、如图:PA、PB切⊙O于A、B,过点C的切线交PA、PB于D、E,PA=8cm,则△PDE的周长为____cm.
13、如图,⊙O切△ABC的BC于D,切AB、AC的延长线于E、F,△ABC的周长为18,则AE=____.
14、如图,AB,AC,BD是⊙O的切线,P,C,D为切点.若AB=5
cm,AC=3
cm,则BD的长为____
cm.
15、如图,△ABC周长为20cm,BC=6cm,圆O是△ABC的内切圆,圆O的切线MN与AB、CA相交于点M、N,则△AMN的周长为________cm.
16、为了测量一个光盘的半径,小周同学把直尺、光盘和三角板按图所示放置于桌面上,并测量出AB=3cm,这张光盘的半径是_____.
17、如图,⊙O是△ABC的内切圆,切点为D,E,F,若AD、BE的长为方程的两个根,
则△ABC的周长为
______.
18、如图,PA、PB、CD是⊙O的切线,A、B、E是切点,CD分别交PA、PB于C、D两点,若∠APB=40°,PA=5,则下列结论:①PA=PB=5;②△PCD的周长为5;③∠COD=70°.正确的有______个.
三、解答题
19、已知:PA、PB、CD分别切⊙O于A、B、E三点,PA=6.求:
(1)△PCD的周长;
(2)若∠P=50°,求∠COD的度数.
20、如图,AB、BC、CD分别与⊙O相切于E、F、G三点,且AB∥CD,OB=6cm,OC=8cm.
(Ⅰ)求证:OB⊥OC;
(Ⅱ)求CG的长.
21、如图,在△ABC中,已知∠ABC=90o,在AB上取一点E,以BE为直径的⊙O恰与AC相切于点D,若AE=2cm,AD=4cm.
(1)求⊙O的直径BE的长;
(2)计算△ABC的面积.
22、如图,AB是⊙O的直径,AM和BN是它的两条切线,DE切⊙O于点E,交AM于点D,交BN于点C,(1)求证:OD∥BE;
(2)如果OD=6cm,OC=8cm,求CD的长.
23、如图,在Rt△ABC中,∠ACB=90°,以AC为直径的⊙O与AB边交于点D,过点D作⊙O的切线.交BC于点E.
(1)求证:BE=EC
(2)填空:①若∠B=30°,AC=2,则DE=______;
②当∠B=______度时,以O,D,E,C为顶点的四边形是正方形.
24、如图,四边形为矩形,以为直径作,过点作与相切于点,连接交于点,连接.
(1)求证:四边形为平行四边形;
(2)若点为的中点,,求的长.
2.5.5切线长定理
-2021-2022学年苏科版九年级数学上册
培优训练(有答案)
一、选择题
1、如图,△ABC的内切圆⊙O与AB,BC,CA分别相切于点D,E,F,且AD=2,BC=5,
则△ABC的周长为( )
A.16
B.14
C.12
D.10
【分析】根据切线长定理进行求解即可.
【详解】∵△ABC的内切圆⊙O与AB,BC,CA分别相切于点D,E,F,
∴AF=AD=2,BD=BE,CE=CF,
∵BE+CE=BC=5,∴BD+CF=BC=5,
∴△ABC的周长=2+2+5+5=14,
故选B.
2、如图,AB是⊙O的直径,点C为⊙O外一点,CA、CD是⊙O的切线,A、D为切点,连接BD、AD.若∠ACD=48°,则∠DBA的大小是( )
A.32°
B.48°
C.60°
D.66°
【分析】根据切线长定理可知CA=CD,求出∠CAD,再证明∠DBA=∠CAD即可解决问题.
【详解】解:∵CA、CD是⊙O的切线,∴CA=CD,
∵∠ACD=48°,∴∠CAD=∠CDA=66°,
∵CA⊥AB,AB是直径,∴∠ADB=∠CAB=90°,
∴∠DBA+∠DAB=90°,∠CAD+∠DAB=90°,∴∠DBA=∠CAD=66°,
故选D.
3、如图,四边形ABCD是⊙O的外切四边形,且AB=10,CD=12,则四边形ABCD的周长为( )
A.44
B.42
C.46
D.47
【答案】A
【分析】根据圆的切线的性质求解即可.
【详解】解:∵四边形ABCD是⊙O的外切四边形,
∴AD+BC=AB+CD=22,
∴四边形ABCD的周长=AD+BC+AB+CD=44,
故选:A.
4、如图,
PA,PB,DE分别切⊙O于点A,B,C,过C的切线分别交PA,PB于点E,D,若△PDE的周长为8,OP=5,则⊙O的半径为( )
A.2
B.3
C.4
D.不能确定
【答案】B
【分析】根据切线长定理得BD=CD,CE=AE,PA=PB,由△PDE的周长为8得到AP=BP=4,连接AO,利用勾股定理即可求出AO,即可求解.
【详解】连接OA.
∵PA、PB、DE分别切⊙O于A、B、C点,
∴BD=CD,CE=AE,PA=PB,OA⊥AP.
∴△PDE的周长为2AP=8,
∴AP=4
在直角三角形OAP中,根据勾股定理,得AO==3,
∴⊙O的半径为3.
故选B.
5、如图,⊙O中,AC为直径,MA,MB分别切⊙O于点A,B,∠BAC=25°,则∠AMB的大小为( )
A.25°
B.30°
C.45°
D.50°
【解析】
【分析】由AM与圆O相切,根据切线的性质得到AM垂直于AC,可得出∠MAC为直角,再由∠BAC的度数,用∠MAC﹣∠BAC求出∠MAB的度数,又MA,MB为圆O的切线,根据切线长定理得到MA=MB,利用等边对等角可得出∠MAB=∠MBA,由底角的度数,利用三角形的内角和定理即可求出∠AMB的度数.
【详解】解:∵MA切⊙O于点A,AC为直径,∴∠MAC=90°,
又∠BAC=25°,∴∠MAB=∠MAC﹣∠BAC=65°,
∵MA、MB分别切⊙O于点A、B,∴MA=MB,∴∠MAB=∠MBA=65°,
∴∠AMB=180°﹣(∠MAB+∠MBA)=50°,
故选:D.
6、如图,PA,PB分别切⊙O于点A,B,OP交⊙O于点C,连接AB,下列结论中,错误的是( )
A.∠1=∠2
B.PA=PB
C.AB⊥OP
D.OP=2OA
【答案】D
【分析】利用切线长定理、等腰三角形的性质即可得出.
【详解】由切线长定理可得:∠1=∠2,PA=PB,从而AB⊥OP.
因此A.B.C都正确.
无法得出AB=PA=PB,可知:D是错误的.
综上可知:只有D是错误的.
故选D.
7、如图,已知、是的两条切线,、为切点,连接交于,交于,连接、,则图中等腰三角形、直角三角形的个数分别为(
)
A.1,2
B.2,2
C.2,6
D.1,6
【答案】C
【分析】根据切线长定理及半径相等得,△APB为等腰三角形,△AOB为等腰三角形,共两个;
根据切线长定理和等腰三角形三线合一的性质,直角三角形有:△AOC,△AOP,△APC,△OBC,△OBP,△CBP,共6个.
【详解】解:因为OA、OB为圆O的半径,所以OA=OB,所以△AOB为等腰三角形,
根据切线长定理,PA=PB,故△APB为等腰三角形,共2个,
根据切线长定理,PA=PB,∠APC=∠BPC,PC=PC,所以△PAC≌△PBC,
故AB⊥PE,根据切线的性质定理∠OAP=∠OBP=90°,
所以直角三角形有:△AOC,△AOP,△APC,△OBC,△OBP,△CBP,共6个.
故选:C.
8、在中,,,的内切圆半径为1,则的周长为(
)
A.13
B.14
C.15
D.16
【分析】根据直角三角形的内切圆的半径等于两条直角边的和与斜边的差的一半,即可求得两条直角边的和,从而求得其周长.
【详解】
解:根据直角三角形的内切圆的半径公式,得,
.
则三角形的周长.
故选B.
9、如图,已知是的两条切线,A,B为切点,线段交于点M.给出下列四种说法:①;②;③四边形有外接圆;④M是外接圆的圆心,
其中正确说法的个数是(
)
A.1
B.2
C.3
D.4
【答案】C
【分析】由切线长定理判断①,结合等腰三角形的性质判断②,利用切线的性质与直角三角形的斜边上的中线等于斜边的一半,判断③,利用反证法判断④.
【详解】解:如图,
是的两条切线,
故①正确,
故②正确,
是的两条切线,
取的中点,连接,则
所以:以为圆心,为半径作圆,则共圆,故③正确,
若M是外接圆的圆心,
与题干提供的条件不符,故④错误,
综上:正确的说法是个,
故选C.
10、如图,直线
AB,BC,CD分别与⊙O相切于E,F,G,且ABCD,若OB=3cm,OC=4cm,则四边形EBCG的周长等于( )
A.5cm
B.10cm
C.cm
D.cm
【答案】C
【分析】连接OF,利用切线性质和切线长定理可证明BE=BF,CG=CF,∠OBE=∠OBF,∠OCG=∠OCF,OF⊥BC,再根据平行线的性质证得∠BOC=90°,进而由勾股定理求得BC长,根据三角形的面积公式求得OF,进而可求得四边形的周长.
【详解】解:连接OF,
∵直线
AB,BC,CD分别与⊙O相切于E,F,G,
∴BE=BF,CG=CF,∠OBE=∠OBF,∠OCG=∠OCF,OF⊥BC,
∵AB∥CD,∴∠ABC+∠DCB=180°,
∴∠OBF+∠OCF=90°,即∠BOC=90°,
∴在Rt△BOC中,OB=3cm,OC=4cm,由勾股定理得:
=5,
由得:OF=
cm,
∴OE=OG=OF=
cm,
∴四边形EBCG的周长为BE+BC+CG+EG=2OE+2BC=2×+2×5=cm,
故选:C.
二、填空题
11、如图,是的切线,为切点,连接.若,则=__________.
【分析】根据切线长定理即可得出AB=AC,然后根据等边对等角和三角形的内角和定理即可求出结论.
【详解】解:∵是的切线,∴AB=AC
∴∠ABC=∠ACB=(180°-∠A)=65°
故答案为:65°.
12、如图:PA、PB切⊙O于A、B,过点C的切线交PA、PB于D、E,PA=8cm,则△PDE的周长为____cm.
【分析】根据切线长定理,即可得到PA=PB,CD=AD,CE=BE,从而求得三角形的周长.
【详解】解:∵PA、PB切⊙O于A、B,DE切⊙O于C,
∴PA=PB=8,CD=AD,CE=BE;
∴△PDE的周长=PD+PE+CD+CE=2PA=16(cm).
故填:16.
13、如图,⊙O切△ABC的BC于D,切AB、AC的延长线于E、F,△ABC的周长为18,则AE=____.
【答案】9.
【分析】根据切线的性质得出BE=BD,DC=CF,进而解答即可.
【详解】解:∵⊙O切△ABC的BC于D,切AB、AC的延长线于E、F,
∴BE=BD,DC=CF,AF=AE,
∵△ABC的周长为18,
即AC+BC+AB=AB+DB+DC+AC=AB+BE+AC+CF=18,
∴AE+AF=18,∴AE=9,
故答案为:9.
14、如图,AB,AC,BD是⊙O的切线,P,C,D为切点.若AB=5
cm,AC=3
cm,则BD的长为____
cm.
【答案】2
【分析】由于AB、AC、BD是⊙O的切线,则AC=AP,BP=BD,求出BP的长即可求出BD的长.
【详解】∵AC、AP为⊙O的切线,∴AC=AP,
∵BP、BD为⊙O的切线,∴BP=BD,
∴BD=PB=AB-AP=5-3=2.
故答案是:2.
15、如图,△ABC周长为20cm,BC=6cm,圆O是△ABC的内切圆,圆O的切线MN与AB、CA相交于点M、N,则△AMN的周长为________cm.
【分析】先作出辅助线,连接切点,利用内切圆的性质得到BE=BF,CE=CG,ME=MH,NG=NH,再利用等量代换即可解题.
【详解】解:∵圆O是△ABC的内切圆,MN是圆O的切线,
如下图,连接各切点,有切线长定理易得,BE=BF,CE=CG,ME=MH,NG=NH,
∵△ABC周长为20cm,
BC=6cm,
∴BC=CE+BE=CG+BF=6cm,
∴△AMN的周长=AM+AN+MN=AM+AN+FM+GN=AF+AG,
又∵AF+AG=AB+AC-(BF+CG)=20-6-6=8cm
故答案是8
16、为了测量一个光盘的半径,小周同学把直尺、光盘和三角板按图所示放置于桌面上,并测量出AB=3cm,这张光盘的半径是_____.
【分析】连接OA,根据题意求出∠OAB=60°,再根据直角三角形的性质和勾股定理求得OB,从而得出光盘的直径.
【详解】如图,作OB⊥AB,连接OA,
∵∠CAD=60°,∴∠CAB=120°,
∵AB和AC与⊙O相切,∴∠OAB=∠OAC,∴∠OAB=∠CAB=60°
∵AB=3cm,∴OA=6cm,
∴由勾股定理得3cm,∴光盘的半径是3cm.
故答案为:3cm.
17、如图,⊙O是△ABC的内切圆,切点为D,E,F,若AD、BE的长为方程的两个根,
则△ABC的周长为
______.
【答案】40;
【解析】如图;解方程,得:x=12,x=5,
∴AD=AF=5,BF=BE=12;AB=17,
设CE=CD=x,则AC=5+x,BC=12+x;
由勾股定理,得:AB2=AC2+BC2,即172=(5+x)2+(12+x)2,
解得:x=3(负值舍去),
∴AC=8,BC=15;
因此△ABC的周长=AC+BC+AB=8+15+17=40,.
故答案为:40.
18、如图,PA、PB、CD是⊙O的切线,A、B、E是切点,CD分别交PA、PB于C、D两点,若∠APB=40°,PA=5,则下列结论:①PA=PB=5;②△PCD的周长为5;③∠COD=70°.正确的有______个.
【分析】根据切线长定理,可判断①正确;将的周长转化为,可判断②错误;连接、、,求出,再由,可判断③正确.
【详解】解:、是的切线,,故①正确;
、、是的切线,,,
的周长,故②错误;
连接、、,,
,故③正确.
综上可得①③正确,共2个.
三、解答题
19、已知:PA、PB、CD分别切⊙O于A、B、E三点,PA=6.求:
(1)△PCD的周长;
(2)若∠P=50°,求∠COD的度数.
【答案】(1)12;(2)
65°.
【解析】
【分析】(1)根据切线长定理,即可得到PA=PB,ED=AD,CE=BC,从而求得三角形的周长=2PA;
(2)连接OE,根据切线的性质得出∠P+∠AOB=180°,由切线长定理得∠COD=
∠AOB,即可得出结果.
解:(1)∵PA、PB切⊙O于A、B,CD切⊙O于E,
∴PA=PB=6,ED=AD,CE=BC;
∴△PCD的周长=PD+DE+PC+CE=2PA=12;
(2)连接OE,如图所示:
由切线的性质得,OA⊥PA,OB⊥PB,OE⊥CD,
∴∠OAC=∠OEC=∠OED=∠OBD=90°,
∴∠AOB+∠P=180°,∴∠AOB=180°﹣∠P=130°,
由切线长定理得:∠AOC=∠EOC,∠EOD=∠BOD,
∴∠COD=∠AOB=×130°=65°.
20、如图,AB、BC、CD分别与⊙O相切于E、F、G三点,且AB∥CD,OB=6cm,OC=8cm.
(Ⅰ)求证:OB⊥OC;
(Ⅱ)求CG的长.
【答案】(Ⅰ)证明见解析
(Ⅱ)6.4cm
【分析】(Ⅰ)根据切线的性质得到OB平分∠EBF,OC平分∠GCF,OF⊥BC,再根据平行线的性质得∠GCF+∠EBF=180°,则有∠OBC+∠OCB=90°,即∠BOC=90°;
(Ⅱ)由勾股定理可求得BC的长,进而由切线长定理即可得到CG的长.
【详解】解:(Ⅰ)连接OF;根据切线长定理得:BE=BF,CF=CG,∠OBF=∠OBE,∠OCF=∠OCG;
∵AB∥CD,∴∠ABC+∠BCD=180°,∴∠OBF+∠OCF=90°,
∴∠BOC=90°,∴OB⊥OC;
(Ⅱ)由(Ⅰ)知,∠BOC=90°.
∵OB=6cm,OC=8cm,
∴由勾股定理得到:BC==10cm,
∴
即
,
∴OF=4.8cm.
∴
=6.4cm,
∵CF、CG分别与⊙O相切于F、G,∴CG=CF=6.4cm.
21、如图,在△ABC中,已知∠ABC=90o,在AB上取一点E,以BE为直径的⊙O恰与AC相切于点D,若AE=2cm,AD=4cm.
(1)求⊙O的直径BE的长;
(2)计算△ABC的面积.
【答案】(1)BE=6;(2)
S△ABC=24..
【分析】(1)连接OD,由切线的性质得OD⊥AC,,在Rt△ODA中运用勾股定理可以求出半径OD,即可求得直径BE的长;
(2)由切线长定理知,CD=BC,在Rt△ABC中运用勾股定理可以求出BC,则可由直角三角形的面积公式求得△ABC的面积.
【详解】(1)连接OD,∴OD⊥AC∴△ODA是直角三角形
设半径为r,
∴AO=r+2,
∴,
解之得:r=3,
∴BE=6
(2)∵∠ABC=900,∴OB⊥BC,
∴BC是⊙O的切线
∵CD切⊙O于D,∴CB=CD
令CB=x,
∴AC=x+4,
CB=x,AB=8
∵,
∴x=6.,
∴S△ABC=24(cm2).
故答案为:(1)BE=6;(2)
S△ABC=24
22、如图,AB是⊙O的直径,AM和BN是它的两条切线,DE切⊙O于点E,交AM于点D,交BN于点C,(1)求证:OD∥BE;
(2)如果OD=6cm,OC=8cm,求CD的长.
【解析】
解:(1)证明:连接OE,
∵AM、DE是⊙O的切线,OA、OE是⊙O的半径,
∴∠ADO=∠EDO,
∠DAO=∠DEO=90°.∴∠AOD=∠EOD=∠AOE.
∵∠ABE=∠AOE,∴∠AOD=∠ABE.∴OD∥BE.
(2)由(1)得:∠AOD=∠EOD=∠AOE,
同理,有:∠BOC=∠EOC=∠BOE.
∴∠AOD+∠EOD+∠BOC+∠EOC=180°.∴∠EOD+∠EOC=90°.
∴△DOC是直角三角形.
∵OD=6cm,OC=8cm,
∴(cm)
.
23、如图,在Rt△ABC中,∠ACB=90°,以AC为直径的⊙O与AB边交于点D,过点D作⊙O的切线.交BC于点E.
(1)求证:BE=EC
(2)填空:①若∠B=30°,AC=2,则DE=______;
②当∠B=______度时,以O,D,E,C为顶点的四边形是正方形.
【答案】(1)见解析;(2)①3;②45.
【分析】(1)证出EC为⊙O的切线;由切线长定理得出EC=ED,再求得EB=ED,即可得出结论;
(2)①由含30°角的直角三角形的性质得出AB,由勾股定理求出BC,再由直角三角形斜边上的中线性质即可得出DE;
②由等腰三角形的性质,得到∠ODA=∠A=45°,于是∠DOC=90°然后根据有一组邻边相等的矩形是正方形,即可得到结论.
【详解】(1)证明:连接DO.
∵∠ACB=90°,AC为直径,∴EC为⊙O的切线;
又∵ED也为⊙O的切线,∴EC=ED,
又∵∠EDO=90°,∴∠BDE+∠ADO=90°,∴∠BDE+∠A=90°
又∵∠B+∠A=90°,∴∠BDE=∠B,∴BE=ED,∴BE=EC;
(2)解:①∵∠ACB=90°,∠B=30°,AC=2,∴AB=2AC=4,∴BC==6,
∵AC为直径,∴∠BDC=∠ADC=90°,
由(1)得:BE=EC,∴DE=BC=3,
故答案为3;
②当∠B=45°时,四边形ODEC是正方形,理由如下:
∵∠ACB=90°,∴∠A=45°,
∵OA=OD,∴∠ADO=45°,∴∠AOD=90°,∴∠DOC=90°,
∵∠ODE=90°,∴四边形DECO是矩形,
∵OD=OC,∴矩形DECO是正方形.
故答案为45.
24、如图,四边形为矩形,以为直径作,过点作与相切于点,连接交于点,连接.
(1)求证:四边形为平行四边形;
(2)若点为的中点,,求的长.
【答案】(1)证明见解析;(2)DC=.
【分析】(1)如图,连接DF、OF,DF交于G,根据AD为直径可得∠AFD=90°,根据切线性质可得∠OFC=90°,根据矩形的性质可得∠ADC=90°,OA//CE,可得DC是切线,根据切线长定理可得CF=DC,由OD=OF可得OC是线段DF的垂直平分线,可得∠OGD=90°,即可证明OC//AE,可得四边形AOCE是平行四边形;
(2)如图,连接OE、OF,由AD=2可得OA=OF=1,由平行四边形的性质可得OA=BE,进而可证明四边形AOEB是矩形,可得∠AOE=90°,OE=AB=CD,根据直角三角形斜边中线的性质可得AE的长,利用勾股定理求出OE的长即可得答案.
【详解】(1)如图,连接DF、OF,DF交于G,
∵AD为直径,∴∠AFD=90°,
∵与相切于点,∴∠OFC=90°,
∵四边形为矩形,∴∠ADC=∠DAB=90°,OA//CE,∴DC是切线,∴DC=CF,
∵OD=OF,∴OC是线段DF的垂直平分线,∴∠OGD=90°,∴OC//AE,
∴四边形AOCE是平行四边形.
(2)如图,连接OE、OF,
∵AD=2,OA=OD,∴OF=OA=1,
∵四边形AOCE是平行四边形,∴OA=CE,
∵AD=BC,∴OA=BE,
∵OA//BE,∴四边形AOEB是平行四边形,
∵∠DAB=90°,∴四边形AOEB是矩形,∴∠AOE=90°,OE=AB=DC,
∵F为AE中点,∴AE=2OF=2,∴DC=OE===.
同课章节目录
- 第1章 一元二次方程
- 1.1 一元二次方程
- 1.2 一元二次方程的解法
- 1.3 一元二次方程的根与系数的关系
- 1.4 用一元二次方程解决问题
- 数学活动 矩形绿地中的花圃设计
- 第2章 对称图形——圆
- 2.1 圆
- 2.2 圆的对称性
- 2.3 确定圆的条件
- 2.4 圆周角
- 2.5 直线与圆的位置关系
- 2.6 正多边形与圆
- 2.7 弧长及扇形的面积
- 2.8 圆锥的侧面积
- 数学活动 图形的密铺
- 第3章 数据的集中趋势和离散程度
- 3.1 平均数
- 3.2 中位数与众数
- 3.3 用计算器求平均数
- 3.4 方差
- 3.5 用计算器求方差
- 数学活动 估测时间
- 第4章 等可能条件下的概率
- 4.1 等可能性
- 4.2 等可能条件下的概率(一)
- 4.3 等可能条件下的概率(二)
- 数学活动 调查“小概率事件”
