2020-2021学年安徽省安庆市宿松县九年级(上)期末数学试卷(Word版 含解析)
文档属性
| 名称 | 2020-2021学年安徽省安庆市宿松县九年级(上)期末数学试卷(Word版 含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-18 06:41:56 | ||
图片预览



文档简介
2020-2021学年安徽省安庆市宿松县九年级第一学期期末数学试卷
一、选择题(本大题共10小题,每小题4分,满分40分。每小题只有一个选项符合题意,请将正确选项的代号填入相应的表格内)
1.抛物线y=(x﹣2020)2+2021的顶点坐标是( )
A.(﹣2020,2021)
B.(2020,2021)
C.(2020,﹣2021)
D.(﹣2020,﹣2021)
2.若反比例函数y=,当x<0时,y随x的增大而增大,则k的取值范围是( )
A.k>﹣2
B.k<﹣2
C.k>2
D.k<2
3.如图,在△ABC中,点D、E分别在边AB、AC上,下列条件中不能判断△ABC∽△AED的是( )
A.∠AED=∠B
B.∠ADE=∠C
C.=
D.=
4.二次函数y=x2,当﹣1≤x≤3时,函数值y的取值范围是( )
A.1≤y≤9
B.0≤y≤9
C.0≤y≤1
D.y≥0
5.比萨斜塔是意大利的著名建筑,其示意图如图所示,设塔顶中心点为点B,塔身中心线AB与垂直中心线AC的夹角为∠A,过点B向垂直中心线AC引垂线,垂足为点D.通过测量可得AB、BD、AD的长度,利用测量所得的数据计算∠A的三角函数值,进而可求∠A的大小.下列关系式正确的是( )
A.sinA=
B.cosA=
C.tanA=
D.sinA=
6.足球运动员将足球沿与地面成一定角度的方向踢出,足球飞行的路线是一条抛物线,不考虑空气阻力,足球距离地面的高度h(单位:m)与足球被踢出后经过的时间t(单位:s)之间的关系如下表:
t
0
1
2
3
4
5
6
7
…
h
0
8
14
18
20
20
18
14
…
下列结论:①足球距离地面的最大高度为20m;②足球飞行路线的对称轴是直线t=;③足球被踢出9s时落地;④足球被踢出1.5s时,距离地面的高度是11m.其中正确结论的个数是( )
A.1
B.2
C.3
D.4
7.如图,Rt△ABC中,∠C=90°,点D在AC上,∠DBC=∠A.若AC=8,cosA=,则BD的长度为( )
A.
B.
C.
D.4
8.我们定义两个不相交的函数图象在竖直方向上的最短距离为这两个函数的“和谐值”.抛物线y=x2﹣2x+3与直线y=x﹣2的“和谐值”为( )
A.3
B.
C.
D.2
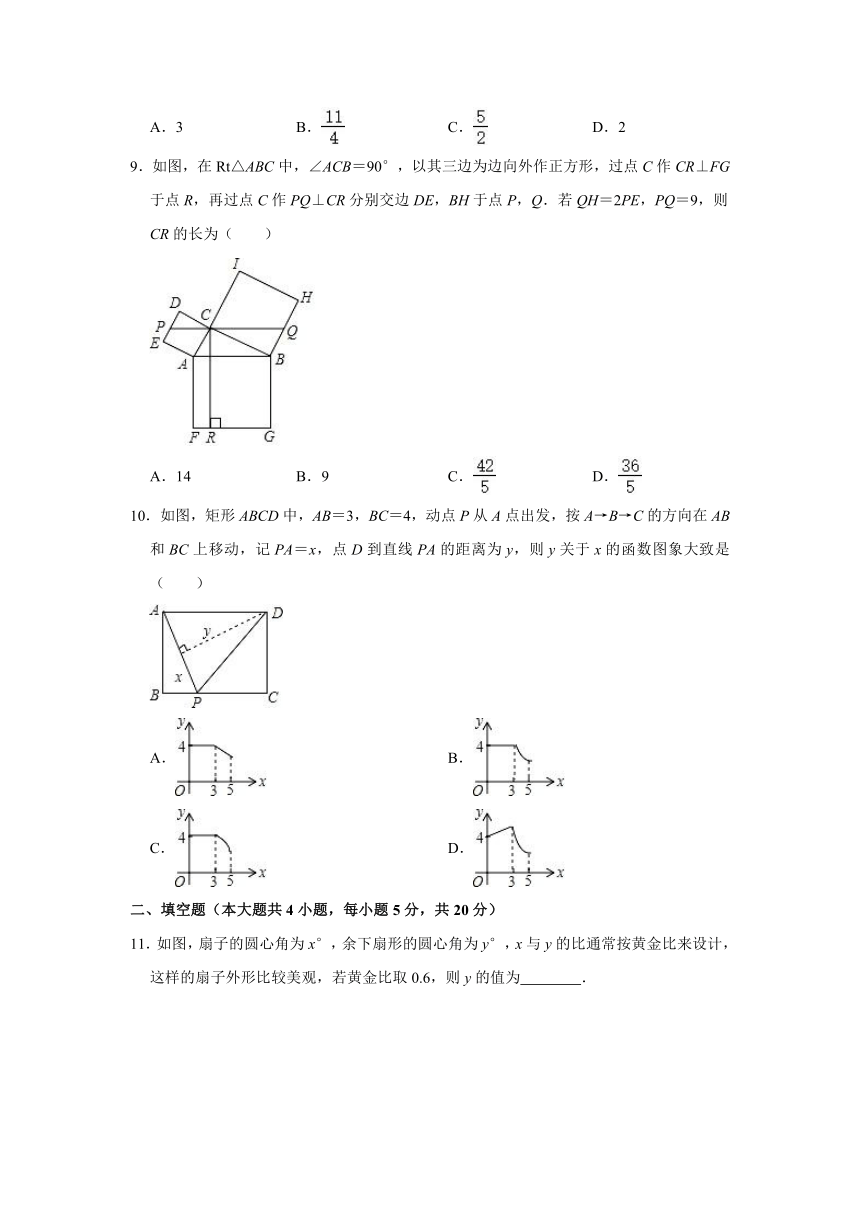
9.如图,在Rt△ABC中,∠ACB=90°,以其三边为边向外作正方形,过点C作CR⊥FG于点R,再过点C作PQ⊥CR分别交边DE,BH于点P,Q.若QH=2PE,PQ=9,则CR的长为( )
A.14
B.9
C.
D.
10.如图,矩形ABCD中,AB=3,BC=4,动点P从A点出发,按A→B→C的方向在AB和BC上移动,记PA=x,点D到直线PA的距离为y,则y关于x的函数图象大致是( )
A.
B.
C.
D.
二、填空题(本大题共4小题,每小题5分,共20分)
11.如图,扇子的圆心角为x°,余下扇形的圆心角为y°,x与y的比通常按黄金比来设计,这样的扇子外形比较美观,若黄金比取0.6,则y的值为
.
12.如图,小明在A时测得某树的影长为1.5m,B时又测得该树的影长为6m,若两次日照的光线互相垂直,则树的高度为
m.
13.如图,一次函数y=x+k(k>0)的图象与x轴和y轴分别交于点A和点B.与反比例函数y=的图象在第一象限内交于点C,CD⊥x轴,CE⊥y轴.垂足分别为点D,E.当矩形ODCE的面积是△OAB的面积2倍时,k的值为
.
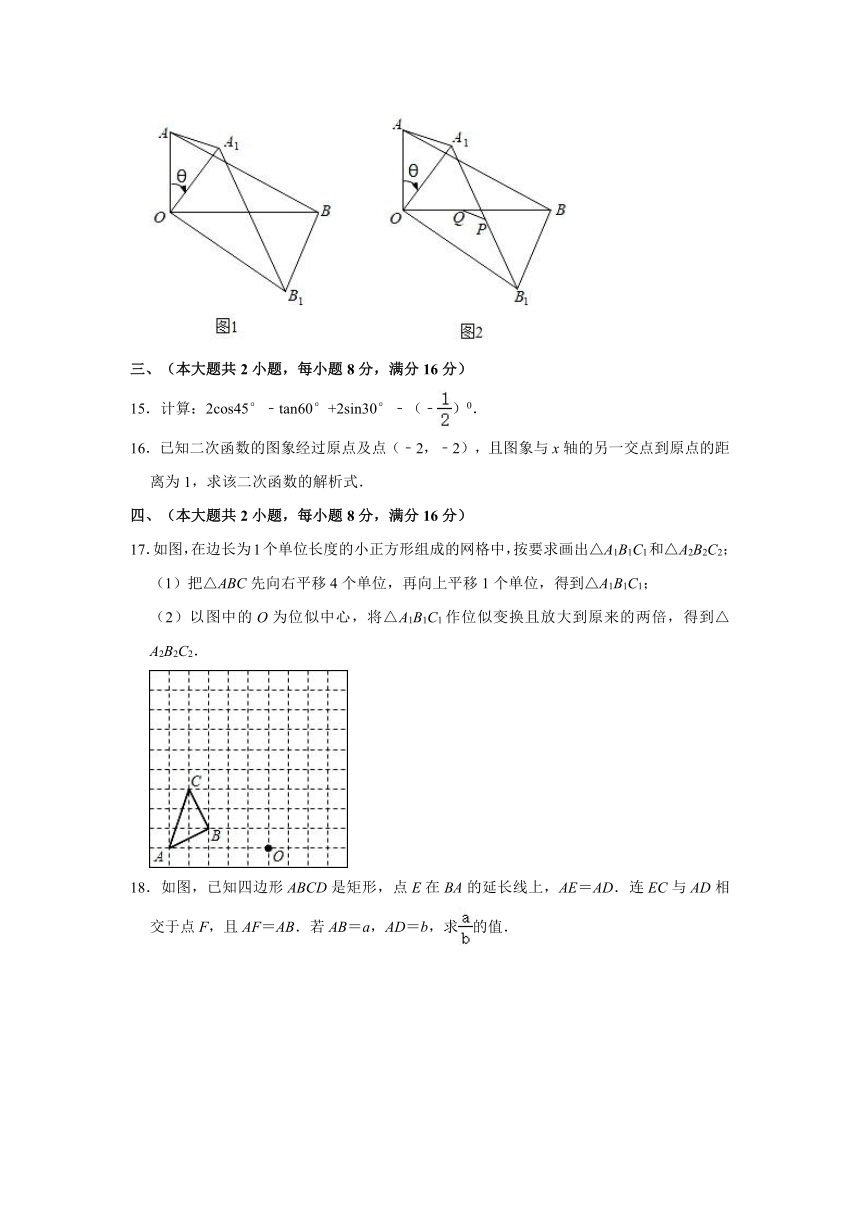
14.在△AOB中,∠AOB=90°,∠ABO=30°,将△AOB绕顶点O顺时针旋转,旋转角为θ(0°<θ<180°),得到△A1OB1.
(1)如图1,连接AA1、BB1,设△AOA1和△BOB1的面积分别为S1、S2,则S1:S2=
.
(2)如图2,设OB中点为Q,A1B1中点为P,连接QP,若AO=1,当θ=
°时,线段QP长度最小,最小值为
.
三、(本大题共2小题,每小题8分,满分16分)
15.计算:2cos45°﹣tan60°+2sin30°﹣(﹣)0.
16.已知二次函数的图象经过原点及点(﹣2,﹣2),且图象与x轴的另一交点到原点的距离为1,求该二次函数的解析式.
四、(本大题共2小题,每小题8分,满分16分)
17.如图,在边长为1个单位长度的小正方形组成的网格中,按要求画出△A1B1C1和△A2B2C2;
(1)把△ABC先向右平移4个单位,再向上平移1个单位,得到△A1B1C1;
(2)以图中的O为位似中心,将△A1B1C1作位似变换且放大到原来的两倍,得到△A2B2C2.
18.如图,已知四边形ABCD是矩形,点E在BA的延长线上,AE=AD.连EC与AD相交于点F,且AF=AB.若AB=a,AD=b,求的值.
五、(本大题共2小题,每小题10分,满分20分)
19.为进一步加强疫情防控工作,避免在测温过程中出现人员聚集现象,某学校决定安装红外线体温检测仪,该设备通过探测人体红外辐射能量对进入测温区域的人员进行快速测温,无需人员停留和接触,安装说明书的部分内容如表.
名称
红外线体温检测仪
安装示意图
技术参数
探测最大角:∠OBC=73.14°
探测最小角:∠OAC=30.97°
安装要求
本设备需安装在垂直于水平地面AC的支架CP上
根据以上内容,解决问题:学校要求测温区域的宽度AB为3m,请你帮助学校确定该设备的安装高度OC.(参考数据:sin73.14°≈0.957,cos73.14°≈0.290,tan73.14°≈3.300,sin30.97°≈0.515,cos30.97°≈0.857,tan30.97°≈0.600)
20.直线y=kx+b与反比例函数y=(x>0)的图象分别交于点A(m,4)和点B(4,n),与坐标轴分别交于点C和点D.
(1)求直线AB的解析式;
(2)观察图象,当x>0时,直接写出kx+b>的解集;
(3)若点P是y轴上一动点,当△COD与△ACP相似时,直接写出点P的坐标.
六、(本题满分12分)
21.如图,O为线段MN的中点,MP与NQ交于点H,∠QOP=∠M=∠N=α,且OQ交MP于D,OP交NH于E.
(1)写出图中两对相似三角形;并证明其中一对.
(2)连接DE,如果α=45°,MN=6,MD=4,求DE的长.
七、(本题满分12分)
22.小红经营的网店以销售文具为主,其中一款笔记本进价为10元/本,拟采取线上和线下两种方式进行销售.调查发现,线下的月销量y(单位:本)与线下售价x(单位:元/本,12≤x≤16,且x为整数)满足一次函数的关系,部分数据如下表:
x(元/本)
12
13
14
15
16
y(本)
120
110
100
90
80
(1)求y与x的函数关系式;
(2)若线上售价始终比线下每本便宜1元,且线上的月销量固定为40件.试问:当x为多少时,线上和线下月利润总和达到最大?并求出此时的最大利润.
八、(本题满分14分)
23.锐角△ABC中,BC=4,S△ABC=6,两动点M,N分别在边AB,AC上滑动,且MN∥BC,以MN为边向下作正方形MPQN,设其边长为x,正方形MPQN与△ABC公共部分的面积为y(y>0);
(1)△ABC中边BC上高AD=
;
(2)当PQ恰好落在边BC上时,求x的值(如图1);
(3)当PQ在△ABC外部时(如图2),求y关于x的函数关系式(注明x的取值范围),并求出x为何值时y最大,最大值是多少?
参考答案
一、选择题(本大题共10小题,每小题4分,满分40分。每小题只有一个选项符合题意,请将正确选项的代号填入相应的表格内)
1.抛物线y=(x﹣2020)2+2021的顶点坐标是( )
A.(﹣2020,2021)
B.(2020,2021)
C.(2020,﹣2021)
D.(﹣2020,﹣2021)
【分析】根据题目中的解析式,即可直接写出抛物线的顶点坐标.
解:∵抛物线的解析式为y=(x﹣2020)2+2021,
∴该抛物线的顶点坐标为(2020,2021),
故选:B.
2.若反比例函数y=,当x<0时,y随x的增大而增大,则k的取值范围是( )
A.k>﹣2
B.k<﹣2
C.k>2
D.k<2
【分析】当k<0,双曲线的两支分别位于第二、第四象限,在每一象限内y随x的增大而增大.根据反比例函数的性质列出关于k的不等式,求出k的取值范围即可.
解:∵反比例函数y=,当x<0时,y随x的增大而增大,
∴k﹣2<0,
解得k<2.
故选:D.
3.如图,在△ABC中,点D、E分别在边AB、AC上,下列条件中不能判断△ABC∽△AED的是( )
A.∠AED=∠B
B.∠ADE=∠C
C.=
D.=
【分析】由于两三角形有公共角,则根据有两组角对应相等的两个三角形相似可对A、B选项进行判断;根据两组对应边的比相等且夹角对应相等的两个三角形相似可对C、D选项进行判断.
解:∵∠DAE=∠CAB,
∴当∠AED=∠B或∠ADE=∠C时,△ABC∽△AED;
当=时,△ABC∽△AED.
故选:D.
4.二次函数y=x2,当﹣1≤x≤3时,函数值y的取值范围是( )
A.1≤y≤9
B.0≤y≤9
C.0≤y≤1
D.y≥0
【分析】由y=x2可知当x=0时,y有最小值是0,再把x=﹣1和3分别代入求得对应y的值,即可求得函数值y的取值范围.
解:∵二次函数y=x2,
∴当x=0时,y有最小值是0,
∵当x=﹣1时,y=1,当x=3时,y=9,
∴当﹣1≤x≤3时,函数值y的取值范围是0≤y≤9,
故选:B.
5.比萨斜塔是意大利的著名建筑,其示意图如图所示,设塔顶中心点为点B,塔身中心线AB与垂直中心线AC的夹角为∠A,过点B向垂直中心线AC引垂线,垂足为点D.通过测量可得AB、BD、AD的长度,利用测量所得的数据计算∠A的三角函数值,进而可求∠A的大小.下列关系式正确的是( )
A.sinA=
B.cosA=
C.tanA=
D.sinA=
【分析】根据直角三角形的边角关系,即锐角三角函数逐个进行判断即可.
解:在Rt△ABD中,∠ADB=90°,
则sinA=,cosA=,tanA=,
因此选项A正确,选项B、C、D不正确;
故选:A.
6.足球运动员将足球沿与地面成一定角度的方向踢出,足球飞行的路线是一条抛物线,不考虑空气阻力,足球距离地面的高度h(单位:m)与足球被踢出后经过的时间t(单位:s)之间的关系如下表:
t
0
1
2
3
4
5
6
7
…
h
0
8
14
18
20
20
18
14
…
下列结论:①足球距离地面的最大高度为20m;②足球飞行路线的对称轴是直线t=;③足球被踢出9s时落地;④足球被踢出1.5s时,距离地面的高度是11m.其中正确结论的个数是( )
A.1
B.2
C.3
D.4
【分析】由题意,抛物线经过(0,0),(9,0),所以可以假设抛物线的解析式为h=at(t﹣9),把(1,8)代入可得a=﹣1,可得h=﹣t2+9t=﹣(t﹣4.5)2+20.25,由此即可一一判断.
解:由题意,抛物线的解析式为h=at(t﹣9),把(1,8)代入可得a=﹣1,
∴h=﹣t2+9t=﹣(t﹣4.5)2+20.25,
∴足球距离地面的最大高度为20.25m,故①错误,
∴抛物线的对称轴t=4.5,故②正确,
∵t=9时,h=0,
∴足球被踢出9s时落地,故③正确,
∵t=1.5时,h=11.25,故④错误.
∴正确的有②③,
故选:B.
7.如图,Rt△ABC中,∠C=90°,点D在AC上,∠DBC=∠A.若AC=8,cosA=,则BD的长度为( )
A.
B.
C.
D.4
【分析】在△ABC中,由锐角三角函数求得AB,再由勾股定理求得BC,证明△BAC∽△DBC,求得BD.
解:∵∠C=90°,AC=8,cosA==,
∴AB=10,
∴BC==6,
∵∠DBC=∠A.∠C=∠C=90°,
∴△BAC∽△DBC,
∴=,
∴=,
∴BD=,
故选:B.
8.我们定义两个不相交的函数图象在竖直方向上的最短距离为这两个函数的“和谐值”.抛物线y=x2﹣2x+3与直线y=x﹣2的“和谐值”为( )
A.3
B.
C.
D.2
【分析】先作出函数图象,在抛物线上取一点P,作PQ∥y轴交直线y=x﹣2于点Q,求出PQ的最小值就是这两个函数的“和谐值”.
解:如图,在抛物线y=x2﹣2x+3上取一点P,作PQ∥y轴交直线y=x﹣2于点Q,
设P(t,t2﹣2t+3),则Q(t,t﹣2),
∴PQ=t2﹣2t+3﹣(t﹣2)
=t2﹣3t+5
=(t﹣)2+,
∴当t=时,PQ有最小值,最小值为,
∴抛物线y=x2﹣2x+3与直线y=x﹣2的“和谐值”为,
故选:B.
9.如图,在Rt△ABC中,∠ACB=90°,以其三边为边向外作正方形,过点C作CR⊥FG于点R,再过点C作PQ⊥CR分别交边DE,BH于点P,Q.若QH=2PE,PQ=9,则CR的长为( )
A.14
B.9
C.
D.
【分析】如图,连接EC,CH.设AB交CR于J.证明△ECP∽△HCQ,推出=,由PQ=9,可得PC=3,CQ=6,由EC:CH=1:2,推出AC:BC=1:2,设AC=a,BC=2a,证明四边形ABQC是平行四边形,推出AB=CQ=6,根据AC2+BC2=AB2,构建方程求出a即可解决问题.
解:如图,连接EC,CH.设AB交CR于J,
∵四边形ACDE,四边形BCIH都是正方形,
∴∠ACE=∠BCH=45°,
∵∠ACB=90°,∠BCI=90°,
∴∠ACE+∠ACB+∠BCH=180°,∠ACB+∠BCI=180°,
∴B,C,D共线,A,C,I共线,E、C、H共线,
∵DE∥AI∥BH,
∴∠CEP=∠CHQ,
∵∠ECP=∠QCH,
∴△ECP∽△HCQ,
∴=,
∵PQ=9,
∴PC=3,CQ=6,
∵EC:CH=1:2,
∴AC:BC=1:2,设AC=a,BC=2a,
∵PQ⊥CR,CR⊥AB,
∴CQ∥AB,
∵AC∥BQ,CQ∥AB,
∴四边形ABQC是平行四边形,
∴AB=CQ=6,
∵AC2+BC2=AB2,
∴5a2=36,
∴a=(负根已经舍弃),
∴AC=,BC=,
∵?AC?BC=?AB?CJ,
∴CJ=,
∵JR=AF=AB=6,
∴CR=CJ+JR=+6=,
故选:C.
10.如图,矩形ABCD中,AB=3,BC=4,动点P从A点出发,按A→B→C的方向在AB和BC上移动,记PA=x,点D到直线PA的距离为y,则y关于x的函数图象大致是( )
A.
B.
C.
D.
【分析】①点P在AB上时,点D到AP的距离为AD的长度,②点P在BC上时,根据同角的余角相等求出∠APB=∠PAD,再利用相似三角形的对应边成比例的性质列出比例式整理得到y与x的关系式,从而得解.
解:①点P在AB上时,0≤x≤3,点D到AP的距离为AD的长度,是定值4;
②点P在BC上时,3<x≤5,
∵∠APB+∠BAP=90°,
∠PAD+∠BAP=90°,
∴∠APB=∠PAD,
又∵∠B=∠DEA=90°,
∴△ABP∽△DEA,
∴=,
即=,
∴y=,
纵观各选项,只有B选项图形符合.
故选:B.
二、填空题(本大题共4小题,每小题5分,共20分)
11.如图,扇子的圆心角为x°,余下扇形的圆心角为y°,x与y的比通常按黄金比来设计,这样的扇子外形比较美观,若黄金比取0.6,则y的值为 225 .
【分析】由题意得到x与y的比值应为黄金比,根据黄金比为0.6,得到x与y比值为0.6,即为3:5,再根据扇子的圆心角与余下的圆心角刚好构成周角,即x与y之和为360,即可求解.
解:由扇子的圆心角为x°,余下扇形的圆心角为y°,黄金比为0.6,
根据题意得:x:y=0.6=3:5,
又∵x+y=360,
则x=360×=225,
故答案为:225.
12.如图,小明在A时测得某树的影长为1.5m,B时又测得该树的影长为6m,若两次日照的光线互相垂直,则树的高度为 3 m.
【分析】根据题意,画出示意图,易得:Rt△EDC∽Rt△FDC,进而可得,即DC2=ED?FD,代入数据可得答案.
解:根据题意,作△EFC,树高为CD,且∠ECF=90°,ED=2m,FD=8m;
∵∠E+∠F=90°,∠E+∠ECD=90°,
∴∠ECD=∠F,
∴Rt△EDC∽Rt△FDC,
∴,即DC2=ED?FD=1.5×6=9,解得CD=3m.
故答案为:3.
13.如图,一次函数y=x+k(k>0)的图象与x轴和y轴分别交于点A和点B.与反比例函数y=的图象在第一象限内交于点C,CD⊥x轴,CE⊥y轴.垂足分别为点D,E.当矩形ODCE的面积是△OAB的面积2倍时,k的值为 1 .
【分析】分别求出矩形ODCE与△OAB的面积,即可求解.
解:一次函数y=x+k(k>0)的图象与x轴和y轴分别交于点A和点B,令x=0,则y=k,令y=0,则x=﹣k,
故点A、B的坐标分别为(﹣k,0)、(0,k),
则△OAB的面积=OA?OB=k2,而矩形ODCE的面积为k,
则2×k2=k,解得:k=0(舍去)或1,
故答案为1.
14.在△AOB中,∠AOB=90°,∠ABO=30°,将△AOB绕顶点O顺时针旋转,旋转角为θ(0°<θ<180°),得到△A1OB1.
(1)如图1,连接AA1、BB1,设△AOA1和△BOB1的面积分别为S1、S2,则S1:S2= .
(2)如图2,设OB中点为Q,A1B1中点为P,连接QP,若AO=1,当θ= 60 °时,线段QP长度最小,最小值为 1﹣ .
【分析】(1)通过证明△AOA1∽△BOB1,由相似三角形的性质可求解;
(2)先求出OP,OQ的长,由三角形的三边关系可得PQ≥OP﹣OQ,则当点Q在线段OP上时,PQ有最小值为1﹣,即可求解.
解:(1)在△AOB中,∠AOB=90°,∠ABO=30°,
∴AB=2AO,OB=OA,
∵将△AOB绕顶点O顺时针旋转,
∴AO=A1O,OB=OB1,∠AOA1=∠BOB1,∠AOB=∠A1OB1=90°,
∴,
∴△AOA1∽△BOB1,
∴S1:S2=()2=,
故答案为:;
(2)如图2,连接OP,
∵AO=1,
∴AB=2AO=2=A1B1,AO=A1O=1,BO=,
∵点Q是OB中点,
∴OQ=,
∵点P是Rt△A1OB1的斜边A1B1的中点,
∴OP=A1P=B1P,
∴A1O=OP=A1P,
∴△A1OP是等边三角形,
∴∠A1OP=60°,
在△OPQ中,PQ≥OP﹣OQ,
∴当点Q在线段OP上时,PQ有最小值为1﹣,
此时θ=60°,
故答案为:60,1﹣.
三、(本大题共2小题,每小题8分,满分16分)
15.计算:2cos45°﹣tan60°+2sin30°﹣(﹣)0.
【分析】直接利用特殊角的三角函数值以及零指数幂的性质分别化简得出答案.
解:原式=2×﹣+2×﹣1
=﹣+1﹣1
=﹣.
16.已知二次函数的图象经过原点及点(﹣2,﹣2),且图象与x轴的另一交点到原点的距离为1,求该二次函数的解析式.
【分析】先确定抛物线与x轴的另一交点的坐标为(1,0)或(﹣1,0),然后利用交点式分别求出两种情况下的抛物线解析式.
解:∵抛物线与x轴的另一交点到原点的距离为1,
∴抛物线与x轴的另一交点的坐标为(1,0)或(﹣1,0),
当抛物线与x轴的另一交点的坐标为(1,0)时,
设抛物线的解析式为y=ax(x﹣1),
把(﹣2,﹣2)代入得a×(﹣2)(﹣2﹣1)=﹣2,解得a=﹣,
∴抛物线的解析式为y=﹣x(x﹣1)
即y=﹣x2+x;
当抛物线与x轴的另一交点的坐标为(﹣1,0)时,
设抛物线的解析式为y=ax(x+1),
把(﹣2,﹣2)代入得a×(﹣2)(﹣2+1)=﹣1,解得a=﹣1,
∴抛物线的解析式为y=﹣x(x﹣1)
即y=﹣x2+x;
综上所述,抛物线的解析式为y=﹣x2+x或y=﹣x2+x.
四、(本大题共2小题,每小题8分,满分16分)
17.如图,在边长为1个单位长度的小正方形组成的网格中,按要求画出△A1B1C1和△A2B2C2;
(1)把△ABC先向右平移4个单位,再向上平移1个单位,得到△A1B1C1;
(2)以图中的O为位似中心,将△A1B1C1作位似变换且放大到原来的两倍,得到△A2B2C2.
【分析】(1)把A、B、C三点先向右平移4个单位,再向上平移1个单位得到A1,B1,C1,顺次连接得到的各点即可;
(2)延长OA1到A2,使OA2=2OA1,同法得到其余各点,顺次连接即可.
解:如图
18.如图,已知四边形ABCD是矩形,点E在BA的延长线上,AE=AD.连EC与AD相交于点F,且AF=AB.若AB=a,AD=b,求的值.
【分析】根据矩形的性质证明△AEF∽△BEC.对应边成比例可得a2+ab=b2,方程两边同时除以b2得,+﹣1=0,解一元二次方程即可得结果.
解:∵四边形ABCD是矩形,
∴AD∥BC,AB=CD,AD=BC,
∴AE=AD=BC=b.AF=AB=a,
∴BE=AE+AB=a+b,
∴△AEF∽△BEC,
∴=,
∴=,
∴a2+ab=b2,
∴+﹣1=0,
解得=(负值舍去),
答:的值为.
五、(本大题共2小题,每小题10分,满分20分)
19.为进一步加强疫情防控工作,避免在测温过程中出现人员聚集现象,某学校决定安装红外线体温检测仪,该设备通过探测人体红外辐射能量对进入测温区域的人员进行快速测温,无需人员停留和接触,安装说明书的部分内容如表.
名称
红外线体温检测仪
安装示意图
技术参数
探测最大角:∠OBC=73.14°
探测最小角:∠OAC=30.97°
安装要求
本设备需安装在垂直于水平地面AC的支架CP上
根据以上内容,解决问题:学校要求测温区域的宽度AB为3m,请你帮助学校确定该设备的安装高度OC.(参考数据:sin73.14°≈0.957,cos73.14°≈0.290,tan73.14°≈3.300,sin30.97°≈0.515,cos30.97°≈0.857,tan30.97°≈0.600)
【分析】根据题意可得OC⊥AC,∠OBC=73.14°,∠OAC=30.97°,AB=3m,所以得AC=AB+BC=3+BC,根据直角三角形锐角三角函数列式计算即可.
解:根据题意可知:
OC⊥AC,∠OBC=73.14°,∠OAC=30.97°,AB=3m,
∴AC=AB+BC=3+BC,
∴在Rt△OBC中,BC=,
在Rt△OAC中,OC=AC?tan∠OAC≈(3+BC)×0.6,
∴OC=0.6(3+),
解得OC=2.2(m).
答:该设备的安装高度OC约为2.2m.
20.直线y=kx+b与反比例函数y=(x>0)的图象分别交于点A(m,4)和点B(4,n),与坐标轴分别交于点C和点D.
(1)求直线AB的解析式;
(2)观察图象,当x>0时,直接写出kx+b>的解集;
(3)若点P是y轴上一动点,当△COD与△ACP相似时,直接写出点P的坐标.
【分析】(1)将点A,B坐标代入双曲线中即可求出m,n,最后将点A,B坐标代入直线解析式中求出k,b即可得到直线AB的解析式;
(2)根据点A,B坐标和图象即可得出结论;
(3)先求出点C,D坐标,进而求出CD,AD,设出点P坐标,最后分两种情况利用相似三角形得出比例式建立方程求解即可得出结论.
解:(1)∵点A(m,4)和点B(4,n)在y=图象上,
∴4=,n=,
∴m=1,n=1,
即A(1,4),B(4,1),
把A(1,4),B(4,1)两点代入y=kx+b中得,
,
解得:,
∴直线AB的解析式为:y=﹣x+5;
(2)由图象可得,当x>0时,kx+b>的解集为1<x<4;
(3)由(1)得直线AB的解析式为y=﹣x+5,
当x=0时,y=5,
∴C(0,5),
∴OC=5,
当y=0时,x=5,
∴D点坐标为(5,0),
∴OD=5,
∴OC=OD,
∴∠OCD=45°
∵A(1,4),
∴AC==,
设P点坐标为(0,a),
由题可知,点P在点C下方,则PC=5﹣a,
∵∠OCD=∠ACP,
①当△COD∽△CPA时,∠APC=∠COD=90°,
∴AP=CP,AP⊥y轴,
∴5﹣a=1,
解得a=4,
故点P坐标为(0,4),
②当△COD∽△PAD时,∠CAP'=∠COD=90°,
∴CP'=AC=2,
∴5﹣a=2,解得a=﹣3,
即点P的坐标为(0,3),
因此,点P的坐标为(0,3)或(0,4)时,△COD与△ADP相似.
六、(本题满分12分)
21.如图,O为线段MN的中点,MP与NQ交于点H,∠QOP=∠M=∠N=α,且OQ交MP于D,OP交NH于E.
(1)写出图中两对相似三角形;并证明其中一对.
(2)连接DE,如果α=45°,MN=6,MD=4,求DE的长.
【分析】(1)利用∠QOP=∠M=∠N=α结合180°通过等量代换得到∠MOD=∠OEN,从而得到△MOD∽△NEO,利用三角形的外角性质,求得△OEN的外角∠OEQ=∠NOQ,得到△QOE∽△QNO;
(2)利用△MOD∽△NEO、MN=6,MD=4,求得EN的长度,由α=45°得到△MNH是等腰直角三角形,从而求得DH和EH,最后利用勾股定理求DE的长.
解:(1)①△MOD∽△NEO,②△QOE∽△QNO,证明如下:
①∵∠QOP=∠M=∠N,
∴∠MOD+∠EON=180°﹣α,∠OEN+∠EON=180°﹣α,
∴∠MOD=∠OEN,
∵∠M=∠N,
∴△MOD∽△NEO;
②∵∠QEO是△OEN的外角,∠N=α,
∴∠QEO=∠N+∠EON=α+∠EON,
又∵∠QON=∠QOE+∠EON=α+∠EON,
∴∠QEO=∠QON,
∵∠QOE=∠N=α,
∴△QOE∽△QNO.
(2)∵∠M=∠N=α=45°,
∴∠MHN=90°,MH=NH,
∴△MHN是等腰直角三角形,
∵MN=6,点O是MN的中点,
∴MH=NH=6,MO=NO=3,
∵△MOD∽△NEO,
∴,
∴,
∴EN=,
∴DH=MH﹣MD=6﹣4=2,EH=NH﹣EN=6﹣=,
∴DE==.
七、(本题满分12分)
22.小红经营的网店以销售文具为主,其中一款笔记本进价为10元/本,拟采取线上和线下两种方式进行销售.调查发现,线下的月销量y(单位:本)与线下售价x(单位:元/本,12≤x≤16,且x为整数)满足一次函数的关系,部分数据如下表:
x(元/本)
12
13
14
15
16
y(本)
120
110
100
90
80
(1)求y与x的函数关系式;
(2)若线上售价始终比线下每本便宜1元,且线上的月销量固定为40件.试问:当x为多少时,线上和线下月利润总和达到最大?并求出此时的最大利润.
【分析】(1)由待定系数法求出y与x的函数关系式即可;
(2)设线上和线下月利润总和为m元,根据题意得到二次函数解析式,由二次函数的性质即可得出答案.
解:(1)∵y与x满足一次函数的关系,
∴设y=kx+b,
将x=12,y=120;x=13,y=110代入得:,
解得:,
∴y与x的函数关系式为:y=﹣10x+240(12≤x≤16);
(2)设线上和线下月利润总和为m元,
则m=40(x﹣10)+y(x﹣10)=40x﹣400+(﹣10x+240)(x﹣10)=﹣10(x﹣19)2+810,
∴当x为19元/件时,线上和线下月利润总和达到最大,此时的最大利润为810元.
八、(本题满分14分)
23.锐角△ABC中,BC=4,S△ABC=6,两动点M,N分别在边AB,AC上滑动,且MN∥BC,以MN为边向下作正方形MPQN,设其边长为x,正方形MPQN与△ABC公共部分的面积为y(y>0);
(1)△ABC中边BC上高AD= 3 ;
(2)当PQ恰好落在边BC上时,求x的值(如图1);
(3)当PQ在△ABC外部时(如图2),求y关于x的函数关系式(注明x的取值范围),并求出x为何值时y最大,最大值是多少?
【分析】(1)利用三角形面积法求出高AD,
(2)利用△AMN与△ABC相似求解.
(3)利用△AMN与△ABC相似求出DE,进而可求出面积.
解:(1)根据题意得:
∵
==6,
∴AD=3.
故答案为3.
(2)设MN与AD交于点E,如图,
∵四边形MNPQ为正方形,
∴MP=MN=x,MN∥BC,
∴△AMN∽△ABC,
∴,即,
解得x=.
(3)设MN与AD交于点E,PM与BC交于点F,如图,
,
设MF=a,则AE=3﹣a,
∵MN∥B,
∴△AMN∽△ABC,
∴,即,
解得:a=3﹣x,
∴公共部分面积:S矩形MNGF=MF×MN=x(3﹣x)=﹣(x﹣2)2+3,
∵当PQ在△ABC外部时,由(2)可得x>,点M,N分别在边AB,AC上可得x≤3,
∴<x≤3,
∴S矩形MNGF=﹣(x﹣2)2+3(<x≤3),
当x=2时,面积有最大值3.
一、选择题(本大题共10小题,每小题4分,满分40分。每小题只有一个选项符合题意,请将正确选项的代号填入相应的表格内)
1.抛物线y=(x﹣2020)2+2021的顶点坐标是( )
A.(﹣2020,2021)
B.(2020,2021)
C.(2020,﹣2021)
D.(﹣2020,﹣2021)
2.若反比例函数y=,当x<0时,y随x的增大而增大,则k的取值范围是( )
A.k>﹣2
B.k<﹣2
C.k>2
D.k<2
3.如图,在△ABC中,点D、E分别在边AB、AC上,下列条件中不能判断△ABC∽△AED的是( )
A.∠AED=∠B
B.∠ADE=∠C
C.=
D.=
4.二次函数y=x2,当﹣1≤x≤3时,函数值y的取值范围是( )
A.1≤y≤9
B.0≤y≤9
C.0≤y≤1
D.y≥0
5.比萨斜塔是意大利的著名建筑,其示意图如图所示,设塔顶中心点为点B,塔身中心线AB与垂直中心线AC的夹角为∠A,过点B向垂直中心线AC引垂线,垂足为点D.通过测量可得AB、BD、AD的长度,利用测量所得的数据计算∠A的三角函数值,进而可求∠A的大小.下列关系式正确的是( )
A.sinA=
B.cosA=
C.tanA=
D.sinA=
6.足球运动员将足球沿与地面成一定角度的方向踢出,足球飞行的路线是一条抛物线,不考虑空气阻力,足球距离地面的高度h(单位:m)与足球被踢出后经过的时间t(单位:s)之间的关系如下表:
t
0
1
2
3
4
5
6
7
…
h
0
8
14
18
20
20
18
14
…
下列结论:①足球距离地面的最大高度为20m;②足球飞行路线的对称轴是直线t=;③足球被踢出9s时落地;④足球被踢出1.5s时,距离地面的高度是11m.其中正确结论的个数是( )
A.1
B.2
C.3
D.4
7.如图,Rt△ABC中,∠C=90°,点D在AC上,∠DBC=∠A.若AC=8,cosA=,则BD的长度为( )
A.
B.
C.
D.4
8.我们定义两个不相交的函数图象在竖直方向上的最短距离为这两个函数的“和谐值”.抛物线y=x2﹣2x+3与直线y=x﹣2的“和谐值”为( )
A.3
B.
C.
D.2
9.如图,在Rt△ABC中,∠ACB=90°,以其三边为边向外作正方形,过点C作CR⊥FG于点R,再过点C作PQ⊥CR分别交边DE,BH于点P,Q.若QH=2PE,PQ=9,则CR的长为( )
A.14
B.9
C.
D.
10.如图,矩形ABCD中,AB=3,BC=4,动点P从A点出发,按A→B→C的方向在AB和BC上移动,记PA=x,点D到直线PA的距离为y,则y关于x的函数图象大致是( )
A.
B.
C.
D.
二、填空题(本大题共4小题,每小题5分,共20分)
11.如图,扇子的圆心角为x°,余下扇形的圆心角为y°,x与y的比通常按黄金比来设计,这样的扇子外形比较美观,若黄金比取0.6,则y的值为
.
12.如图,小明在A时测得某树的影长为1.5m,B时又测得该树的影长为6m,若两次日照的光线互相垂直,则树的高度为
m.
13.如图,一次函数y=x+k(k>0)的图象与x轴和y轴分别交于点A和点B.与反比例函数y=的图象在第一象限内交于点C,CD⊥x轴,CE⊥y轴.垂足分别为点D,E.当矩形ODCE的面积是△OAB的面积2倍时,k的值为
.
14.在△AOB中,∠AOB=90°,∠ABO=30°,将△AOB绕顶点O顺时针旋转,旋转角为θ(0°<θ<180°),得到△A1OB1.
(1)如图1,连接AA1、BB1,设△AOA1和△BOB1的面积分别为S1、S2,则S1:S2=
.
(2)如图2,设OB中点为Q,A1B1中点为P,连接QP,若AO=1,当θ=
°时,线段QP长度最小,最小值为
.
三、(本大题共2小题,每小题8分,满分16分)
15.计算:2cos45°﹣tan60°+2sin30°﹣(﹣)0.
16.已知二次函数的图象经过原点及点(﹣2,﹣2),且图象与x轴的另一交点到原点的距离为1,求该二次函数的解析式.
四、(本大题共2小题,每小题8分,满分16分)
17.如图,在边长为1个单位长度的小正方形组成的网格中,按要求画出△A1B1C1和△A2B2C2;
(1)把△ABC先向右平移4个单位,再向上平移1个单位,得到△A1B1C1;
(2)以图中的O为位似中心,将△A1B1C1作位似变换且放大到原来的两倍,得到△A2B2C2.
18.如图,已知四边形ABCD是矩形,点E在BA的延长线上,AE=AD.连EC与AD相交于点F,且AF=AB.若AB=a,AD=b,求的值.
五、(本大题共2小题,每小题10分,满分20分)
19.为进一步加强疫情防控工作,避免在测温过程中出现人员聚集现象,某学校决定安装红外线体温检测仪,该设备通过探测人体红外辐射能量对进入测温区域的人员进行快速测温,无需人员停留和接触,安装说明书的部分内容如表.
名称
红外线体温检测仪
安装示意图
技术参数
探测最大角:∠OBC=73.14°
探测最小角:∠OAC=30.97°
安装要求
本设备需安装在垂直于水平地面AC的支架CP上
根据以上内容,解决问题:学校要求测温区域的宽度AB为3m,请你帮助学校确定该设备的安装高度OC.(参考数据:sin73.14°≈0.957,cos73.14°≈0.290,tan73.14°≈3.300,sin30.97°≈0.515,cos30.97°≈0.857,tan30.97°≈0.600)
20.直线y=kx+b与反比例函数y=(x>0)的图象分别交于点A(m,4)和点B(4,n),与坐标轴分别交于点C和点D.
(1)求直线AB的解析式;
(2)观察图象,当x>0时,直接写出kx+b>的解集;
(3)若点P是y轴上一动点,当△COD与△ACP相似时,直接写出点P的坐标.
六、(本题满分12分)
21.如图,O为线段MN的中点,MP与NQ交于点H,∠QOP=∠M=∠N=α,且OQ交MP于D,OP交NH于E.
(1)写出图中两对相似三角形;并证明其中一对.
(2)连接DE,如果α=45°,MN=6,MD=4,求DE的长.
七、(本题满分12分)
22.小红经营的网店以销售文具为主,其中一款笔记本进价为10元/本,拟采取线上和线下两种方式进行销售.调查发现,线下的月销量y(单位:本)与线下售价x(单位:元/本,12≤x≤16,且x为整数)满足一次函数的关系,部分数据如下表:
x(元/本)
12
13
14
15
16
y(本)
120
110
100
90
80
(1)求y与x的函数关系式;
(2)若线上售价始终比线下每本便宜1元,且线上的月销量固定为40件.试问:当x为多少时,线上和线下月利润总和达到最大?并求出此时的最大利润.
八、(本题满分14分)
23.锐角△ABC中,BC=4,S△ABC=6,两动点M,N分别在边AB,AC上滑动,且MN∥BC,以MN为边向下作正方形MPQN,设其边长为x,正方形MPQN与△ABC公共部分的面积为y(y>0);
(1)△ABC中边BC上高AD=
;
(2)当PQ恰好落在边BC上时,求x的值(如图1);
(3)当PQ在△ABC外部时(如图2),求y关于x的函数关系式(注明x的取值范围),并求出x为何值时y最大,最大值是多少?
参考答案
一、选择题(本大题共10小题,每小题4分,满分40分。每小题只有一个选项符合题意,请将正确选项的代号填入相应的表格内)
1.抛物线y=(x﹣2020)2+2021的顶点坐标是( )
A.(﹣2020,2021)
B.(2020,2021)
C.(2020,﹣2021)
D.(﹣2020,﹣2021)
【分析】根据题目中的解析式,即可直接写出抛物线的顶点坐标.
解:∵抛物线的解析式为y=(x﹣2020)2+2021,
∴该抛物线的顶点坐标为(2020,2021),
故选:B.
2.若反比例函数y=,当x<0时,y随x的增大而增大,则k的取值范围是( )
A.k>﹣2
B.k<﹣2
C.k>2
D.k<2
【分析】当k<0,双曲线的两支分别位于第二、第四象限,在每一象限内y随x的增大而增大.根据反比例函数的性质列出关于k的不等式,求出k的取值范围即可.
解:∵反比例函数y=,当x<0时,y随x的增大而增大,
∴k﹣2<0,
解得k<2.
故选:D.
3.如图,在△ABC中,点D、E分别在边AB、AC上,下列条件中不能判断△ABC∽△AED的是( )
A.∠AED=∠B
B.∠ADE=∠C
C.=
D.=
【分析】由于两三角形有公共角,则根据有两组角对应相等的两个三角形相似可对A、B选项进行判断;根据两组对应边的比相等且夹角对应相等的两个三角形相似可对C、D选项进行判断.
解:∵∠DAE=∠CAB,
∴当∠AED=∠B或∠ADE=∠C时,△ABC∽△AED;
当=时,△ABC∽△AED.
故选:D.
4.二次函数y=x2,当﹣1≤x≤3时,函数值y的取值范围是( )
A.1≤y≤9
B.0≤y≤9
C.0≤y≤1
D.y≥0
【分析】由y=x2可知当x=0时,y有最小值是0,再把x=﹣1和3分别代入求得对应y的值,即可求得函数值y的取值范围.
解:∵二次函数y=x2,
∴当x=0时,y有最小值是0,
∵当x=﹣1时,y=1,当x=3时,y=9,
∴当﹣1≤x≤3时,函数值y的取值范围是0≤y≤9,
故选:B.
5.比萨斜塔是意大利的著名建筑,其示意图如图所示,设塔顶中心点为点B,塔身中心线AB与垂直中心线AC的夹角为∠A,过点B向垂直中心线AC引垂线,垂足为点D.通过测量可得AB、BD、AD的长度,利用测量所得的数据计算∠A的三角函数值,进而可求∠A的大小.下列关系式正确的是( )
A.sinA=
B.cosA=
C.tanA=
D.sinA=
【分析】根据直角三角形的边角关系,即锐角三角函数逐个进行判断即可.
解:在Rt△ABD中,∠ADB=90°,
则sinA=,cosA=,tanA=,
因此选项A正确,选项B、C、D不正确;
故选:A.
6.足球运动员将足球沿与地面成一定角度的方向踢出,足球飞行的路线是一条抛物线,不考虑空气阻力,足球距离地面的高度h(单位:m)与足球被踢出后经过的时间t(单位:s)之间的关系如下表:
t
0
1
2
3
4
5
6
7
…
h
0
8
14
18
20
20
18
14
…
下列结论:①足球距离地面的最大高度为20m;②足球飞行路线的对称轴是直线t=;③足球被踢出9s时落地;④足球被踢出1.5s时,距离地面的高度是11m.其中正确结论的个数是( )
A.1
B.2
C.3
D.4
【分析】由题意,抛物线经过(0,0),(9,0),所以可以假设抛物线的解析式为h=at(t﹣9),把(1,8)代入可得a=﹣1,可得h=﹣t2+9t=﹣(t﹣4.5)2+20.25,由此即可一一判断.
解:由题意,抛物线的解析式为h=at(t﹣9),把(1,8)代入可得a=﹣1,
∴h=﹣t2+9t=﹣(t﹣4.5)2+20.25,
∴足球距离地面的最大高度为20.25m,故①错误,
∴抛物线的对称轴t=4.5,故②正确,
∵t=9时,h=0,
∴足球被踢出9s时落地,故③正确,
∵t=1.5时,h=11.25,故④错误.
∴正确的有②③,
故选:B.
7.如图,Rt△ABC中,∠C=90°,点D在AC上,∠DBC=∠A.若AC=8,cosA=,则BD的长度为( )
A.
B.
C.
D.4
【分析】在△ABC中,由锐角三角函数求得AB,再由勾股定理求得BC,证明△BAC∽△DBC,求得BD.
解:∵∠C=90°,AC=8,cosA==,
∴AB=10,
∴BC==6,
∵∠DBC=∠A.∠C=∠C=90°,
∴△BAC∽△DBC,
∴=,
∴=,
∴BD=,
故选:B.
8.我们定义两个不相交的函数图象在竖直方向上的最短距离为这两个函数的“和谐值”.抛物线y=x2﹣2x+3与直线y=x﹣2的“和谐值”为( )
A.3
B.
C.
D.2
【分析】先作出函数图象,在抛物线上取一点P,作PQ∥y轴交直线y=x﹣2于点Q,求出PQ的最小值就是这两个函数的“和谐值”.
解:如图,在抛物线y=x2﹣2x+3上取一点P,作PQ∥y轴交直线y=x﹣2于点Q,
设P(t,t2﹣2t+3),则Q(t,t﹣2),
∴PQ=t2﹣2t+3﹣(t﹣2)
=t2﹣3t+5
=(t﹣)2+,
∴当t=时,PQ有最小值,最小值为,
∴抛物线y=x2﹣2x+3与直线y=x﹣2的“和谐值”为,
故选:B.
9.如图,在Rt△ABC中,∠ACB=90°,以其三边为边向外作正方形,过点C作CR⊥FG于点R,再过点C作PQ⊥CR分别交边DE,BH于点P,Q.若QH=2PE,PQ=9,则CR的长为( )
A.14
B.9
C.
D.
【分析】如图,连接EC,CH.设AB交CR于J.证明△ECP∽△HCQ,推出=,由PQ=9,可得PC=3,CQ=6,由EC:CH=1:2,推出AC:BC=1:2,设AC=a,BC=2a,证明四边形ABQC是平行四边形,推出AB=CQ=6,根据AC2+BC2=AB2,构建方程求出a即可解决问题.
解:如图,连接EC,CH.设AB交CR于J,
∵四边形ACDE,四边形BCIH都是正方形,
∴∠ACE=∠BCH=45°,
∵∠ACB=90°,∠BCI=90°,
∴∠ACE+∠ACB+∠BCH=180°,∠ACB+∠BCI=180°,
∴B,C,D共线,A,C,I共线,E、C、H共线,
∵DE∥AI∥BH,
∴∠CEP=∠CHQ,
∵∠ECP=∠QCH,
∴△ECP∽△HCQ,
∴=,
∵PQ=9,
∴PC=3,CQ=6,
∵EC:CH=1:2,
∴AC:BC=1:2,设AC=a,BC=2a,
∵PQ⊥CR,CR⊥AB,
∴CQ∥AB,
∵AC∥BQ,CQ∥AB,
∴四边形ABQC是平行四边形,
∴AB=CQ=6,
∵AC2+BC2=AB2,
∴5a2=36,
∴a=(负根已经舍弃),
∴AC=,BC=,
∵?AC?BC=?AB?CJ,
∴CJ=,
∵JR=AF=AB=6,
∴CR=CJ+JR=+6=,
故选:C.
10.如图,矩形ABCD中,AB=3,BC=4,动点P从A点出发,按A→B→C的方向在AB和BC上移动,记PA=x,点D到直线PA的距离为y,则y关于x的函数图象大致是( )
A.
B.
C.
D.
【分析】①点P在AB上时,点D到AP的距离为AD的长度,②点P在BC上时,根据同角的余角相等求出∠APB=∠PAD,再利用相似三角形的对应边成比例的性质列出比例式整理得到y与x的关系式,从而得解.
解:①点P在AB上时,0≤x≤3,点D到AP的距离为AD的长度,是定值4;
②点P在BC上时,3<x≤5,
∵∠APB+∠BAP=90°,
∠PAD+∠BAP=90°,
∴∠APB=∠PAD,
又∵∠B=∠DEA=90°,
∴△ABP∽△DEA,
∴=,
即=,
∴y=,
纵观各选项,只有B选项图形符合.
故选:B.
二、填空题(本大题共4小题,每小题5分,共20分)
11.如图,扇子的圆心角为x°,余下扇形的圆心角为y°,x与y的比通常按黄金比来设计,这样的扇子外形比较美观,若黄金比取0.6,则y的值为 225 .
【分析】由题意得到x与y的比值应为黄金比,根据黄金比为0.6,得到x与y比值为0.6,即为3:5,再根据扇子的圆心角与余下的圆心角刚好构成周角,即x与y之和为360,即可求解.
解:由扇子的圆心角为x°,余下扇形的圆心角为y°,黄金比为0.6,
根据题意得:x:y=0.6=3:5,
又∵x+y=360,
则x=360×=225,
故答案为:225.
12.如图,小明在A时测得某树的影长为1.5m,B时又测得该树的影长为6m,若两次日照的光线互相垂直,则树的高度为 3 m.
【分析】根据题意,画出示意图,易得:Rt△EDC∽Rt△FDC,进而可得,即DC2=ED?FD,代入数据可得答案.
解:根据题意,作△EFC,树高为CD,且∠ECF=90°,ED=2m,FD=8m;
∵∠E+∠F=90°,∠E+∠ECD=90°,
∴∠ECD=∠F,
∴Rt△EDC∽Rt△FDC,
∴,即DC2=ED?FD=1.5×6=9,解得CD=3m.
故答案为:3.
13.如图,一次函数y=x+k(k>0)的图象与x轴和y轴分别交于点A和点B.与反比例函数y=的图象在第一象限内交于点C,CD⊥x轴,CE⊥y轴.垂足分别为点D,E.当矩形ODCE的面积是△OAB的面积2倍时,k的值为 1 .
【分析】分别求出矩形ODCE与△OAB的面积,即可求解.
解:一次函数y=x+k(k>0)的图象与x轴和y轴分别交于点A和点B,令x=0,则y=k,令y=0,则x=﹣k,
故点A、B的坐标分别为(﹣k,0)、(0,k),
则△OAB的面积=OA?OB=k2,而矩形ODCE的面积为k,
则2×k2=k,解得:k=0(舍去)或1,
故答案为1.
14.在△AOB中,∠AOB=90°,∠ABO=30°,将△AOB绕顶点O顺时针旋转,旋转角为θ(0°<θ<180°),得到△A1OB1.
(1)如图1,连接AA1、BB1,设△AOA1和△BOB1的面积分别为S1、S2,则S1:S2= .
(2)如图2,设OB中点为Q,A1B1中点为P,连接QP,若AO=1,当θ= 60 °时,线段QP长度最小,最小值为 1﹣ .
【分析】(1)通过证明△AOA1∽△BOB1,由相似三角形的性质可求解;
(2)先求出OP,OQ的长,由三角形的三边关系可得PQ≥OP﹣OQ,则当点Q在线段OP上时,PQ有最小值为1﹣,即可求解.
解:(1)在△AOB中,∠AOB=90°,∠ABO=30°,
∴AB=2AO,OB=OA,
∵将△AOB绕顶点O顺时针旋转,
∴AO=A1O,OB=OB1,∠AOA1=∠BOB1,∠AOB=∠A1OB1=90°,
∴,
∴△AOA1∽△BOB1,
∴S1:S2=()2=,
故答案为:;
(2)如图2,连接OP,
∵AO=1,
∴AB=2AO=2=A1B1,AO=A1O=1,BO=,
∵点Q是OB中点,
∴OQ=,
∵点P是Rt△A1OB1的斜边A1B1的中点,
∴OP=A1P=B1P,
∴A1O=OP=A1P,
∴△A1OP是等边三角形,
∴∠A1OP=60°,
在△OPQ中,PQ≥OP﹣OQ,
∴当点Q在线段OP上时,PQ有最小值为1﹣,
此时θ=60°,
故答案为:60,1﹣.
三、(本大题共2小题,每小题8分,满分16分)
15.计算:2cos45°﹣tan60°+2sin30°﹣(﹣)0.
【分析】直接利用特殊角的三角函数值以及零指数幂的性质分别化简得出答案.
解:原式=2×﹣+2×﹣1
=﹣+1﹣1
=﹣.
16.已知二次函数的图象经过原点及点(﹣2,﹣2),且图象与x轴的另一交点到原点的距离为1,求该二次函数的解析式.
【分析】先确定抛物线与x轴的另一交点的坐标为(1,0)或(﹣1,0),然后利用交点式分别求出两种情况下的抛物线解析式.
解:∵抛物线与x轴的另一交点到原点的距离为1,
∴抛物线与x轴的另一交点的坐标为(1,0)或(﹣1,0),
当抛物线与x轴的另一交点的坐标为(1,0)时,
设抛物线的解析式为y=ax(x﹣1),
把(﹣2,﹣2)代入得a×(﹣2)(﹣2﹣1)=﹣2,解得a=﹣,
∴抛物线的解析式为y=﹣x(x﹣1)
即y=﹣x2+x;
当抛物线与x轴的另一交点的坐标为(﹣1,0)时,
设抛物线的解析式为y=ax(x+1),
把(﹣2,﹣2)代入得a×(﹣2)(﹣2+1)=﹣1,解得a=﹣1,
∴抛物线的解析式为y=﹣x(x﹣1)
即y=﹣x2+x;
综上所述,抛物线的解析式为y=﹣x2+x或y=﹣x2+x.
四、(本大题共2小题,每小题8分,满分16分)
17.如图,在边长为1个单位长度的小正方形组成的网格中,按要求画出△A1B1C1和△A2B2C2;
(1)把△ABC先向右平移4个单位,再向上平移1个单位,得到△A1B1C1;
(2)以图中的O为位似中心,将△A1B1C1作位似变换且放大到原来的两倍,得到△A2B2C2.
【分析】(1)把A、B、C三点先向右平移4个单位,再向上平移1个单位得到A1,B1,C1,顺次连接得到的各点即可;
(2)延长OA1到A2,使OA2=2OA1,同法得到其余各点,顺次连接即可.
解:如图
18.如图,已知四边形ABCD是矩形,点E在BA的延长线上,AE=AD.连EC与AD相交于点F,且AF=AB.若AB=a,AD=b,求的值.
【分析】根据矩形的性质证明△AEF∽△BEC.对应边成比例可得a2+ab=b2,方程两边同时除以b2得,+﹣1=0,解一元二次方程即可得结果.
解:∵四边形ABCD是矩形,
∴AD∥BC,AB=CD,AD=BC,
∴AE=AD=BC=b.AF=AB=a,
∴BE=AE+AB=a+b,
∴△AEF∽△BEC,
∴=,
∴=,
∴a2+ab=b2,
∴+﹣1=0,
解得=(负值舍去),
答:的值为.
五、(本大题共2小题,每小题10分,满分20分)
19.为进一步加强疫情防控工作,避免在测温过程中出现人员聚集现象,某学校决定安装红外线体温检测仪,该设备通过探测人体红外辐射能量对进入测温区域的人员进行快速测温,无需人员停留和接触,安装说明书的部分内容如表.
名称
红外线体温检测仪
安装示意图
技术参数
探测最大角:∠OBC=73.14°
探测最小角:∠OAC=30.97°
安装要求
本设备需安装在垂直于水平地面AC的支架CP上
根据以上内容,解决问题:学校要求测温区域的宽度AB为3m,请你帮助学校确定该设备的安装高度OC.(参考数据:sin73.14°≈0.957,cos73.14°≈0.290,tan73.14°≈3.300,sin30.97°≈0.515,cos30.97°≈0.857,tan30.97°≈0.600)
【分析】根据题意可得OC⊥AC,∠OBC=73.14°,∠OAC=30.97°,AB=3m,所以得AC=AB+BC=3+BC,根据直角三角形锐角三角函数列式计算即可.
解:根据题意可知:
OC⊥AC,∠OBC=73.14°,∠OAC=30.97°,AB=3m,
∴AC=AB+BC=3+BC,
∴在Rt△OBC中,BC=,
在Rt△OAC中,OC=AC?tan∠OAC≈(3+BC)×0.6,
∴OC=0.6(3+),
解得OC=2.2(m).
答:该设备的安装高度OC约为2.2m.
20.直线y=kx+b与反比例函数y=(x>0)的图象分别交于点A(m,4)和点B(4,n),与坐标轴分别交于点C和点D.
(1)求直线AB的解析式;
(2)观察图象,当x>0时,直接写出kx+b>的解集;
(3)若点P是y轴上一动点,当△COD与△ACP相似时,直接写出点P的坐标.
【分析】(1)将点A,B坐标代入双曲线中即可求出m,n,最后将点A,B坐标代入直线解析式中求出k,b即可得到直线AB的解析式;
(2)根据点A,B坐标和图象即可得出结论;
(3)先求出点C,D坐标,进而求出CD,AD,设出点P坐标,最后分两种情况利用相似三角形得出比例式建立方程求解即可得出结论.
解:(1)∵点A(m,4)和点B(4,n)在y=图象上,
∴4=,n=,
∴m=1,n=1,
即A(1,4),B(4,1),
把A(1,4),B(4,1)两点代入y=kx+b中得,
,
解得:,
∴直线AB的解析式为:y=﹣x+5;
(2)由图象可得,当x>0时,kx+b>的解集为1<x<4;
(3)由(1)得直线AB的解析式为y=﹣x+5,
当x=0时,y=5,
∴C(0,5),
∴OC=5,
当y=0时,x=5,
∴D点坐标为(5,0),
∴OD=5,
∴OC=OD,
∴∠OCD=45°
∵A(1,4),
∴AC==,
设P点坐标为(0,a),
由题可知,点P在点C下方,则PC=5﹣a,
∵∠OCD=∠ACP,
①当△COD∽△CPA时,∠APC=∠COD=90°,
∴AP=CP,AP⊥y轴,
∴5﹣a=1,
解得a=4,
故点P坐标为(0,4),
②当△COD∽△PAD时,∠CAP'=∠COD=90°,
∴CP'=AC=2,
∴5﹣a=2,解得a=﹣3,
即点P的坐标为(0,3),
因此,点P的坐标为(0,3)或(0,4)时,△COD与△ADP相似.
六、(本题满分12分)
21.如图,O为线段MN的中点,MP与NQ交于点H,∠QOP=∠M=∠N=α,且OQ交MP于D,OP交NH于E.
(1)写出图中两对相似三角形;并证明其中一对.
(2)连接DE,如果α=45°,MN=6,MD=4,求DE的长.
【分析】(1)利用∠QOP=∠M=∠N=α结合180°通过等量代换得到∠MOD=∠OEN,从而得到△MOD∽△NEO,利用三角形的外角性质,求得△OEN的外角∠OEQ=∠NOQ,得到△QOE∽△QNO;
(2)利用△MOD∽△NEO、MN=6,MD=4,求得EN的长度,由α=45°得到△MNH是等腰直角三角形,从而求得DH和EH,最后利用勾股定理求DE的长.
解:(1)①△MOD∽△NEO,②△QOE∽△QNO,证明如下:
①∵∠QOP=∠M=∠N,
∴∠MOD+∠EON=180°﹣α,∠OEN+∠EON=180°﹣α,
∴∠MOD=∠OEN,
∵∠M=∠N,
∴△MOD∽△NEO;
②∵∠QEO是△OEN的外角,∠N=α,
∴∠QEO=∠N+∠EON=α+∠EON,
又∵∠QON=∠QOE+∠EON=α+∠EON,
∴∠QEO=∠QON,
∵∠QOE=∠N=α,
∴△QOE∽△QNO.
(2)∵∠M=∠N=α=45°,
∴∠MHN=90°,MH=NH,
∴△MHN是等腰直角三角形,
∵MN=6,点O是MN的中点,
∴MH=NH=6,MO=NO=3,
∵△MOD∽△NEO,
∴,
∴,
∴EN=,
∴DH=MH﹣MD=6﹣4=2,EH=NH﹣EN=6﹣=,
∴DE==.
七、(本题满分12分)
22.小红经营的网店以销售文具为主,其中一款笔记本进价为10元/本,拟采取线上和线下两种方式进行销售.调查发现,线下的月销量y(单位:本)与线下售价x(单位:元/本,12≤x≤16,且x为整数)满足一次函数的关系,部分数据如下表:
x(元/本)
12
13
14
15
16
y(本)
120
110
100
90
80
(1)求y与x的函数关系式;
(2)若线上售价始终比线下每本便宜1元,且线上的月销量固定为40件.试问:当x为多少时,线上和线下月利润总和达到最大?并求出此时的最大利润.
【分析】(1)由待定系数法求出y与x的函数关系式即可;
(2)设线上和线下月利润总和为m元,根据题意得到二次函数解析式,由二次函数的性质即可得出答案.
解:(1)∵y与x满足一次函数的关系,
∴设y=kx+b,
将x=12,y=120;x=13,y=110代入得:,
解得:,
∴y与x的函数关系式为:y=﹣10x+240(12≤x≤16);
(2)设线上和线下月利润总和为m元,
则m=40(x﹣10)+y(x﹣10)=40x﹣400+(﹣10x+240)(x﹣10)=﹣10(x﹣19)2+810,
∴当x为19元/件时,线上和线下月利润总和达到最大,此时的最大利润为810元.
八、(本题满分14分)
23.锐角△ABC中,BC=4,S△ABC=6,两动点M,N分别在边AB,AC上滑动,且MN∥BC,以MN为边向下作正方形MPQN,设其边长为x,正方形MPQN与△ABC公共部分的面积为y(y>0);
(1)△ABC中边BC上高AD= 3 ;
(2)当PQ恰好落在边BC上时,求x的值(如图1);
(3)当PQ在△ABC外部时(如图2),求y关于x的函数关系式(注明x的取值范围),并求出x为何值时y最大,最大值是多少?
【分析】(1)利用三角形面积法求出高AD,
(2)利用△AMN与△ABC相似求解.
(3)利用△AMN与△ABC相似求出DE,进而可求出面积.
解:(1)根据题意得:
∵
==6,
∴AD=3.
故答案为3.
(2)设MN与AD交于点E,如图,
∵四边形MNPQ为正方形,
∴MP=MN=x,MN∥BC,
∴△AMN∽△ABC,
∴,即,
解得x=.
(3)设MN与AD交于点E,PM与BC交于点F,如图,
,
设MF=a,则AE=3﹣a,
∵MN∥B,
∴△AMN∽△ABC,
∴,即,
解得:a=3﹣x,
∴公共部分面积:S矩形MNGF=MF×MN=x(3﹣x)=﹣(x﹣2)2+3,
∵当PQ在△ABC外部时,由(2)可得x>,点M,N分别在边AB,AC上可得x≤3,
∴<x≤3,
∴S矩形MNGF=﹣(x﹣2)2+3(<x≤3),
当x=2时,面积有最大值3.
同课章节目录
