人教版2021年八年级上册:12.1全等三角形 课时练习卷(Word版含解析)
文档属性
| 名称 | 人教版2021年八年级上册:12.1全等三角形 课时练习卷(Word版含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 112.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-18 09:02:57 | ||
图片预览


文档简介
人教版2021年八年级上册:12.1全等三角形
课时练习卷
一.选择题
1.下列各组中的两个图形为全等形的是( )
A.两块三角尺
B.两枚硬币
C.两张A4纸
D.两片枫树叶
2.下列说法正确的是( )
A.形状相同的两个三角形全等
B.面积相等的两个三角形全等
C.完全重合的两个三角形全等
D.所有的等边三角形全等
3.如图,△ABC≌△DEC,A和D,B和E是对应点,B、C、D在同一直线上,且CE=5,AC=7,则BD的长为( )
A.12
B.7
C.2
D.14
4.如图,△ABC≌△DEF,DF和AC,EF和BC为对应边,若∠A=123°,∠F=39°,则∠DEF等于( )
A.18°
B.20°
C.39°
D.123°
5.如图,△ABC≌△A'B'C',其中∠A=36°,∠C'=24°,则∠B=( )
A.60°
B.100°
C.120°
D.135°
6.已知△ABC≌△DEF,∠A=∠B=30°,则∠E的度数是( )
A.30°
B.120°
C.60°
D.90°
7.如图,△ABC≌△ADE,则下列结论正确的个数是( )
①AB=AD;②∠E=∠C;③若∠BAE=120°,∠BAD=40°,则∠BAC=80°;④BC=DE.
A.1
B.2
C.3
D.4
二.填空题
8.如图,四边形ABCD≌四边形A′B′C′D′,则∠A的大小是
.
9.如图,若△ABC≌△ADE,且∠1=35°,则∠2=
.
10.如图,若△ABC≌△DEF,则x的值为
.
11.如果△ABC的三边长分别为7,5,3,△DEF的三边长分别为3x﹣2,2x﹣1,3,若这两个三角形全等,则x=
.
12.如图,已知△ABD≌△ACE,∠A=53°,∠B=22°,则∠C=
°.
三.解答题
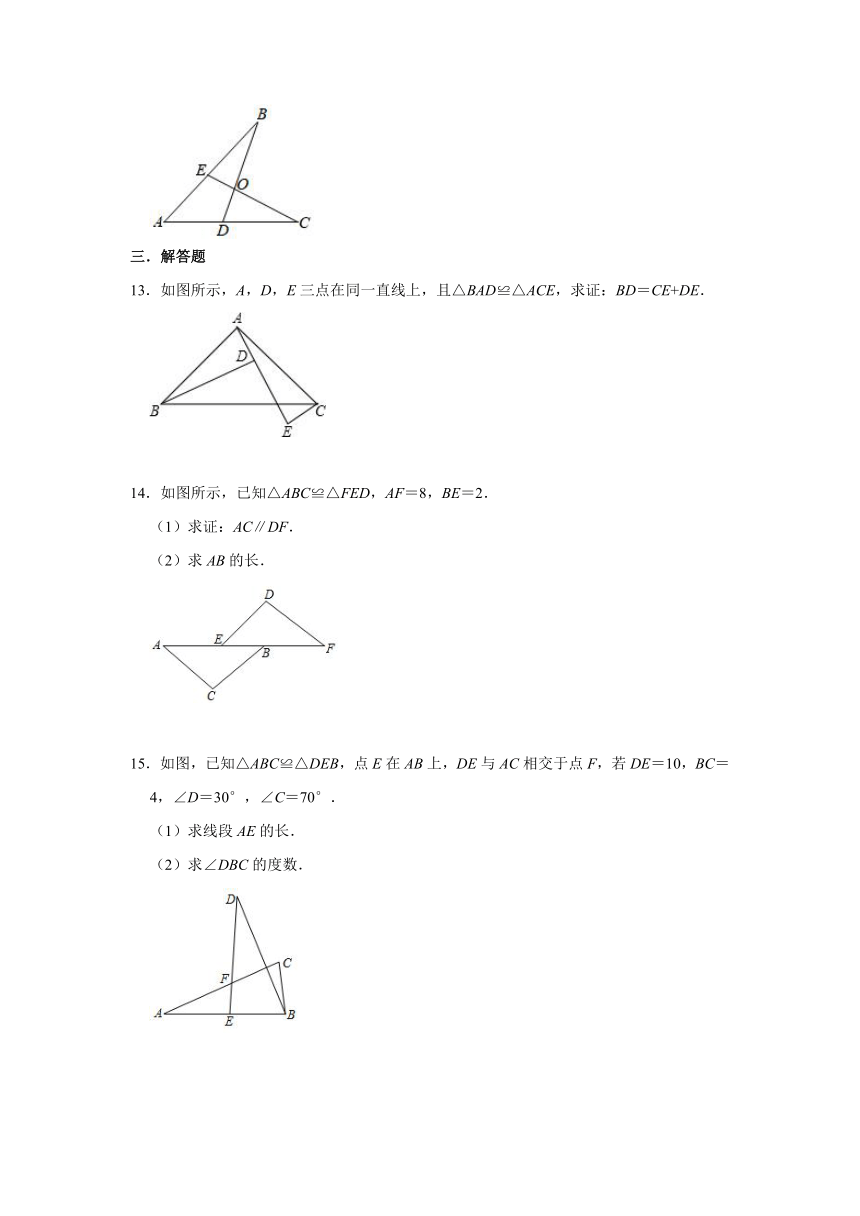
13.如图所示,A,D,E三点在同一直线上,且△BAD≌△ACE,求证:BD=CE+DE.
14.如图所示,已知△ABC≌△FED,AF=8,BE=2.
(1)求证:AC∥DF.
(2)求AB的长.
15.如图,已知△ABC≌△DEB,点E在AB上,DE与AC相交于点F,若DE=10,BC=4,∠D=30°,∠C=70°.
(1)求线段AE的长.
(2)求∠DBC的度数.
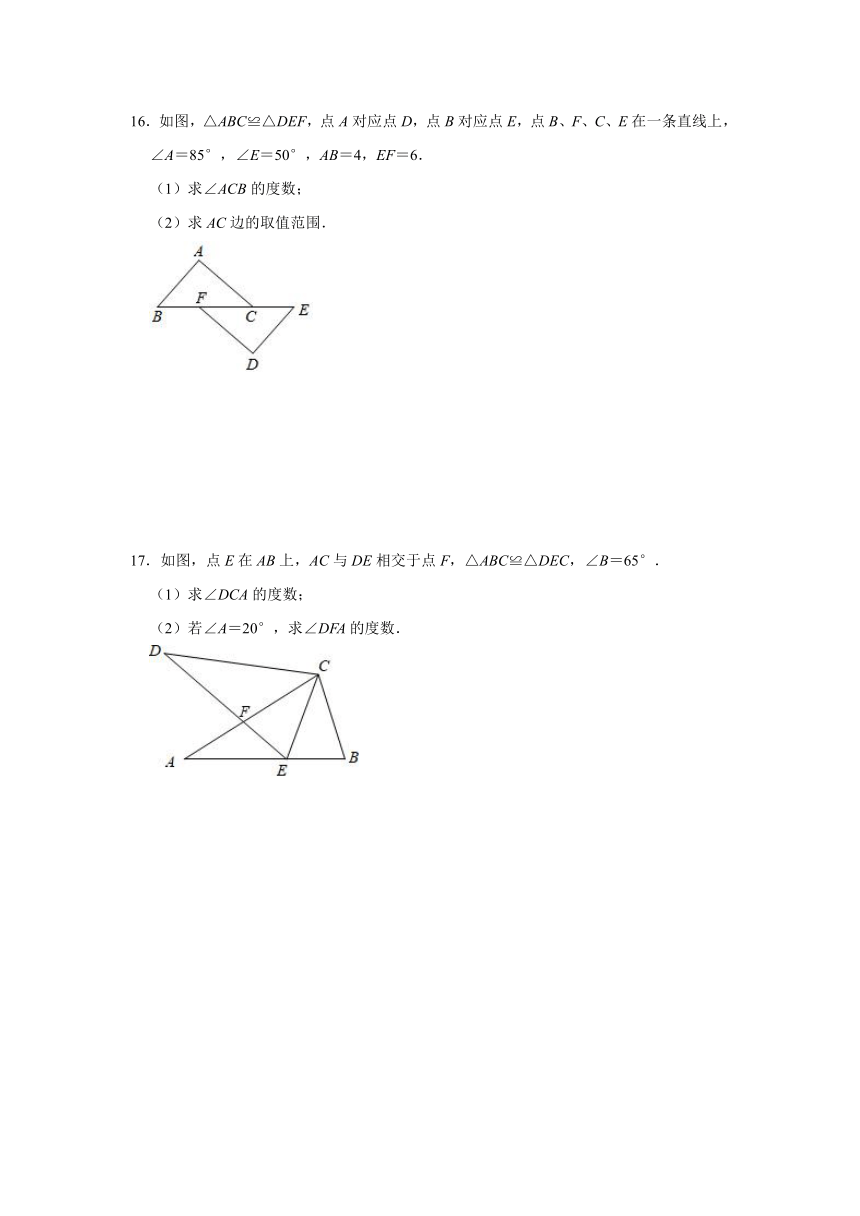
16.如图,△ABC≌△DEF,点A对应点D,点B对应点E,点B、F、C、E在一条直线上,∠A=85°,∠E=50°,AB=4,EF=6.
(1)求∠ACB的度数;
(2)求AC边的取值范围.
17.如图,点E在AB上,AC与DE相交于点F,△ABC≌△DEC,∠B=65°.
(1)求∠DCA的度数;
(2)若∠A=20°,求∠DFA的度数.
参考答案
一.选择题
1.解:A、两块三角尺不一定是全等形,故此选项不合题意;
B、两枚硬币不一定是全等形,故此选项不合题意;
C、两张A4纸是全等形,故此选项符合题意;
D、两片枫树叶不一定是全等形,故此选项不合题意;
故选:C.
2.解:A、形状相同的两个三角形全等,说法错误,应该是形状相同且大小也相同的两个三角形全等;
B、面积相等的两个三角形全等,说法错误;
C、完全重合的两个三角形全等,说法正确;
D、所有的等边三角形全等,说法错误;
故选:C.
3.解:如图,△ABC≌△DEC,A和D,B和E是对应点,B、C、D在同一直线上,且CE=5,AC=7,
∴BC=EC=5,CD=AC=7,
∴BD=BC+CD=12.
故选:A.
4.解;∵△ABC≌△DEF,∠A=123°,
∴∠D=∠A=123°,
∵∠F=39°,
∴∠DEF=180°﹣123°﹣39°=18°,
故选:A.
5.解:∵△ABC≌△A'B'C',∠C'=24°,
∴∠C=∠C'=24°,
∴∠B=180°﹣∠A﹣∠C=180°﹣36°﹣24°=120°,
故选:C.
6.解:∵△ABC≌△DEF,∠A=∠B=30°,
∴∠D=∠E=∠A=∠B=30°,
则∠E的度数是30°.
故选:A.
7.解:∵△ABC≌△ADE,
∴AB=AD;∠E=∠C;BC=DE,∠BAC=∠DAE,
∴∠BAC﹣∠BAD=∠DAE﹣∠DAC,
即∠BAD=∠CAE,
∵∠BAE=120°,∠BAD=40°,
∴∠CAE=40°,
∴∠BAC=∠BAE﹣∠CAE=80°,
∴①②③④都正确,
故选:D.
二.填空题
8.解:∵四边形ABCD≌四边形A'B'C'D',
∴∠D=∠D′=130°,
∴∠A=360°﹣∠B﹣∠C﹣∠D=360°﹣75°﹣60°﹣130°=95°,
故答案为:95°.
9.解:∵△ABC≌△ADE,
∴∠EAD=∠CAB,
∴∠1=∠2=35°.
故答案为:35°.
10.解:∵△ABC≌△DEF,
∴EF=BC,
∵BC=30,EF=x,
∴x=30,
故答案为:30.
11.解:∵△ABC与△DEF全等,
∴3x﹣2+2x﹣1+3=3+5+7,解得x=3,
故答案为:3.
12.解:∵△ABD≌△ACE,
∴∠C=∠B,
∵∠B=22°,
∴∠C=22°,
故答案为:22.
三.解答题
13.解:∵△BAD≌△ACE,
∴BD=AE,AD=CE,
∴BD=AE=AD+DE=CE+DE,
即BD=DE+CE.
14.证明:(1)∵△ABC≌△FED,
∴∠A=∠F.
∴AC∥DF.
(2)∵△ABC≌△FED,
∴AB=EF.
∴AB﹣EB=EF﹣EB.
∴AE=BF.
∵AF=8,BE=2
∴AE+BF=8﹣2=6
∴AE=3
∴AB=AE+BE=3+2=5
15.解:(1)∵△ABC≌△DEB,DE=10,BC=4,
∴AB=DE=10,BE=BC=4,
∴AE=AB﹣BE=6;
(2)∵△ABC≌△DEB,∠D=30°,∠C=70°,
∴∠BAC=∠D=30°,∠DBE=∠C=70°,
∴∠ABC=180°﹣30°﹣70°=80°,
∴∠DBC=∠ABC﹣∠DBE=10°.
16.解:(1)∵△ABC≌△DEF,
∴∠B=∠E=50°,
∵∠A=85°,
∴∠ACB=180°﹣∠B﹣∠A=45°;
(2)∵△ABC≌△DEF,
∴BC=EF=6,
∵AB=4,
∴6﹣4<AC<6+4,
∴AC边的取值范围为:2<AC<10.
17.(1)证明:∵△ABC≌△DEC,
∴CB=CE,∠DCE=∠ACB,
∴∠CEB=∠B=65°,
在△BEC中,∠CEB+∠B+∠ECB=180°,
∴∠ECB=180°﹣65°﹣65°=50°,
又∠DCE=∠ACB,
∴∠DCA=∠ECB=50°;
(2)解:∵△ABC≌△DEC,
∴∠D=∠A=20°,
在△DFC中,
∠DFA=∠DCA+∠D=50°+20°=70°.
课时练习卷
一.选择题
1.下列各组中的两个图形为全等形的是( )
A.两块三角尺
B.两枚硬币
C.两张A4纸
D.两片枫树叶
2.下列说法正确的是( )
A.形状相同的两个三角形全等
B.面积相等的两个三角形全等
C.完全重合的两个三角形全等
D.所有的等边三角形全等
3.如图,△ABC≌△DEC,A和D,B和E是对应点,B、C、D在同一直线上,且CE=5,AC=7,则BD的长为( )
A.12
B.7
C.2
D.14
4.如图,△ABC≌△DEF,DF和AC,EF和BC为对应边,若∠A=123°,∠F=39°,则∠DEF等于( )
A.18°
B.20°
C.39°
D.123°
5.如图,△ABC≌△A'B'C',其中∠A=36°,∠C'=24°,则∠B=( )
A.60°
B.100°
C.120°
D.135°
6.已知△ABC≌△DEF,∠A=∠B=30°,则∠E的度数是( )
A.30°
B.120°
C.60°
D.90°
7.如图,△ABC≌△ADE,则下列结论正确的个数是( )
①AB=AD;②∠E=∠C;③若∠BAE=120°,∠BAD=40°,则∠BAC=80°;④BC=DE.
A.1
B.2
C.3
D.4
二.填空题
8.如图,四边形ABCD≌四边形A′B′C′D′,则∠A的大小是
.
9.如图,若△ABC≌△ADE,且∠1=35°,则∠2=
.
10.如图,若△ABC≌△DEF,则x的值为
.
11.如果△ABC的三边长分别为7,5,3,△DEF的三边长分别为3x﹣2,2x﹣1,3,若这两个三角形全等,则x=
.
12.如图,已知△ABD≌△ACE,∠A=53°,∠B=22°,则∠C=
°.
三.解答题
13.如图所示,A,D,E三点在同一直线上,且△BAD≌△ACE,求证:BD=CE+DE.
14.如图所示,已知△ABC≌△FED,AF=8,BE=2.
(1)求证:AC∥DF.
(2)求AB的长.
15.如图,已知△ABC≌△DEB,点E在AB上,DE与AC相交于点F,若DE=10,BC=4,∠D=30°,∠C=70°.
(1)求线段AE的长.
(2)求∠DBC的度数.
16.如图,△ABC≌△DEF,点A对应点D,点B对应点E,点B、F、C、E在一条直线上,∠A=85°,∠E=50°,AB=4,EF=6.
(1)求∠ACB的度数;
(2)求AC边的取值范围.
17.如图,点E在AB上,AC与DE相交于点F,△ABC≌△DEC,∠B=65°.
(1)求∠DCA的度数;
(2)若∠A=20°,求∠DFA的度数.
参考答案
一.选择题
1.解:A、两块三角尺不一定是全等形,故此选项不合题意;
B、两枚硬币不一定是全等形,故此选项不合题意;
C、两张A4纸是全等形,故此选项符合题意;
D、两片枫树叶不一定是全等形,故此选项不合题意;
故选:C.
2.解:A、形状相同的两个三角形全等,说法错误,应该是形状相同且大小也相同的两个三角形全等;
B、面积相等的两个三角形全等,说法错误;
C、完全重合的两个三角形全等,说法正确;
D、所有的等边三角形全等,说法错误;
故选:C.
3.解:如图,△ABC≌△DEC,A和D,B和E是对应点,B、C、D在同一直线上,且CE=5,AC=7,
∴BC=EC=5,CD=AC=7,
∴BD=BC+CD=12.
故选:A.
4.解;∵△ABC≌△DEF,∠A=123°,
∴∠D=∠A=123°,
∵∠F=39°,
∴∠DEF=180°﹣123°﹣39°=18°,
故选:A.
5.解:∵△ABC≌△A'B'C',∠C'=24°,
∴∠C=∠C'=24°,
∴∠B=180°﹣∠A﹣∠C=180°﹣36°﹣24°=120°,
故选:C.
6.解:∵△ABC≌△DEF,∠A=∠B=30°,
∴∠D=∠E=∠A=∠B=30°,
则∠E的度数是30°.
故选:A.
7.解:∵△ABC≌△ADE,
∴AB=AD;∠E=∠C;BC=DE,∠BAC=∠DAE,
∴∠BAC﹣∠BAD=∠DAE﹣∠DAC,
即∠BAD=∠CAE,
∵∠BAE=120°,∠BAD=40°,
∴∠CAE=40°,
∴∠BAC=∠BAE﹣∠CAE=80°,
∴①②③④都正确,
故选:D.
二.填空题
8.解:∵四边形ABCD≌四边形A'B'C'D',
∴∠D=∠D′=130°,
∴∠A=360°﹣∠B﹣∠C﹣∠D=360°﹣75°﹣60°﹣130°=95°,
故答案为:95°.
9.解:∵△ABC≌△ADE,
∴∠EAD=∠CAB,
∴∠1=∠2=35°.
故答案为:35°.
10.解:∵△ABC≌△DEF,
∴EF=BC,
∵BC=30,EF=x,
∴x=30,
故答案为:30.
11.解:∵△ABC与△DEF全等,
∴3x﹣2+2x﹣1+3=3+5+7,解得x=3,
故答案为:3.
12.解:∵△ABD≌△ACE,
∴∠C=∠B,
∵∠B=22°,
∴∠C=22°,
故答案为:22.
三.解答题
13.解:∵△BAD≌△ACE,
∴BD=AE,AD=CE,
∴BD=AE=AD+DE=CE+DE,
即BD=DE+CE.
14.证明:(1)∵△ABC≌△FED,
∴∠A=∠F.
∴AC∥DF.
(2)∵△ABC≌△FED,
∴AB=EF.
∴AB﹣EB=EF﹣EB.
∴AE=BF.
∵AF=8,BE=2
∴AE+BF=8﹣2=6
∴AE=3
∴AB=AE+BE=3+2=5
15.解:(1)∵△ABC≌△DEB,DE=10,BC=4,
∴AB=DE=10,BE=BC=4,
∴AE=AB﹣BE=6;
(2)∵△ABC≌△DEB,∠D=30°,∠C=70°,
∴∠BAC=∠D=30°,∠DBE=∠C=70°,
∴∠ABC=180°﹣30°﹣70°=80°,
∴∠DBC=∠ABC﹣∠DBE=10°.
16.解:(1)∵△ABC≌△DEF,
∴∠B=∠E=50°,
∵∠A=85°,
∴∠ACB=180°﹣∠B﹣∠A=45°;
(2)∵△ABC≌△DEF,
∴BC=EF=6,
∵AB=4,
∴6﹣4<AC<6+4,
∴AC边的取值范围为:2<AC<10.
17.(1)证明:∵△ABC≌△DEC,
∴CB=CE,∠DCE=∠ACB,
∴∠CEB=∠B=65°,
在△BEC中,∠CEB+∠B+∠ECB=180°,
∴∠ECB=180°﹣65°﹣65°=50°,
又∠DCE=∠ACB,
∴∠DCA=∠ECB=50°;
(2)解:∵△ABC≌△DEC,
∴∠D=∠A=20°,
在△DFC中,
∠DFA=∠DCA+∠D=50°+20°=70°.
