1.5加速度(2012)

(共25张PPT)
第一章 运动的描述
§1.5速度变化快慢的描述－加速度
普通的小型轿车和旅客列车，速度都能达到108km/h。但是，它们起步后达到这样的速度所需的时间是不一样的。例如一辆小汽车起步时在20s内速度达到了108km/h，而一列火车达到这个速度大约要用300s。
思考与讨论
问：它们的速度平均1s各增加多少？
谁的速度“增加”得比较快？
　　 “速度大” “速度变化大”“速度变化得快”描述的三种情况是否相同 ？
跑车加速性能的比较
一、加速度
1.定义：速度的变化量与发生这一变化所用时间的比值
——初速度
——末速度
2.定义式：
a ——加速度
4.物理意义：描述速度变化的快慢及方向.(数值等于单位时间内速度的变化量，即速度的变化率)
读作：米每二次方秒
3.单位：在国际单位制中，加速度的单位是m/s2
——速度改变量
(比值法定义).
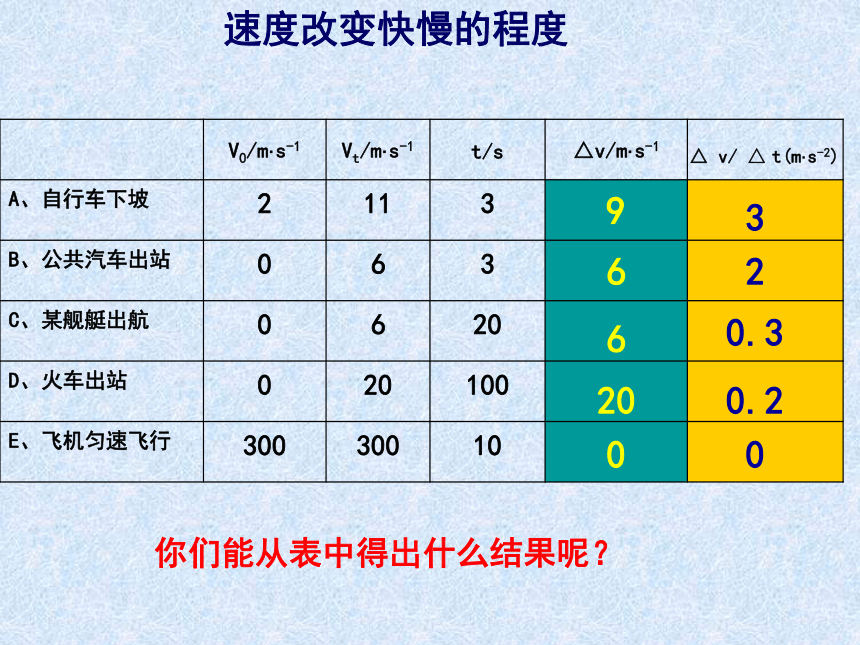
V0/m·s-1 Vt/m·s-1 t/s △v/m·s-1
A、自行车下坡 2 11 3
B、公共汽车出站 0 6 3
C、某舰艇出航 0 6 20
D、火车出站 0 20 100
E、飞机匀速飞行 300 300 10
△ v/ △ t(m·s-2)
3
2
0.3
0.2
0
你们能从表中得出什么结果呢？
速度改变快慢的程度
9
6
0
6
20
例1、 迫击炮射击时，炮弹在弹筒中的速度在0.005s 就可以从0增加到250m/s ，这时迫击炮的加速度为多少？
解：
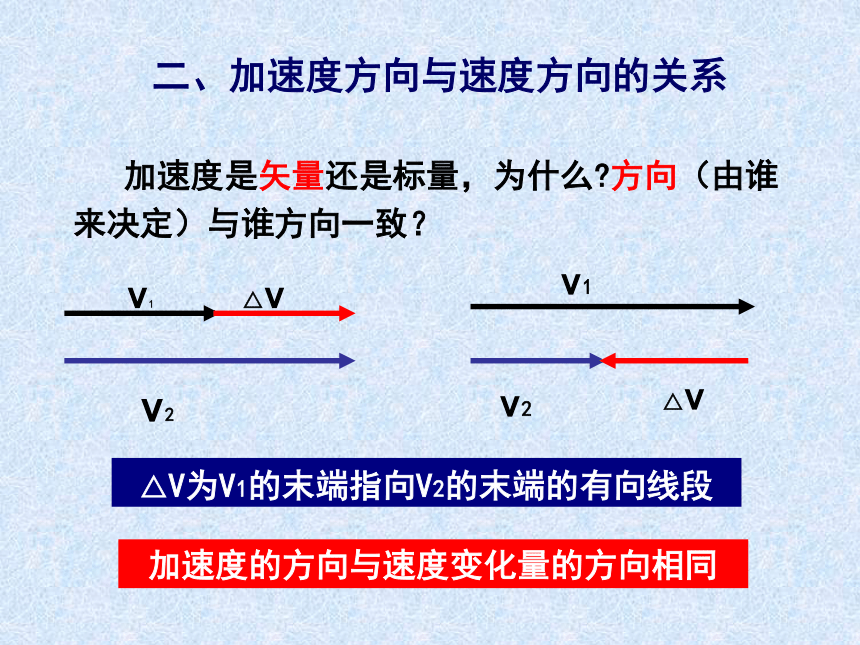
加速度是矢量还是标量，为什么 方向（由谁来决定）与谁方向一致？
v1
v2
△v
v1
v2
△v
二、加速度方向与速度方向的关系
加速度的方向与速度变化量的方向相同
△V为V1的末端指向V2的末端的有向线段
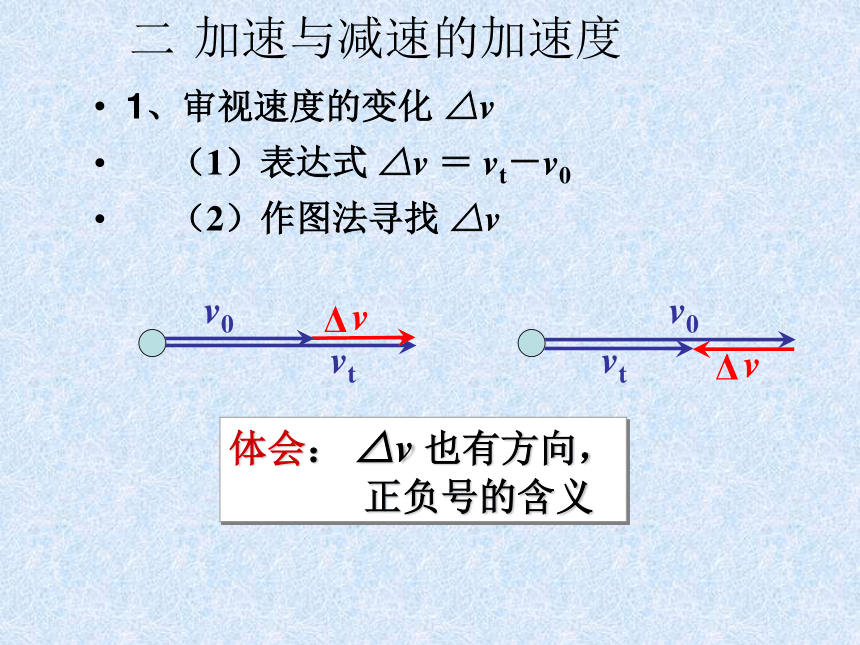
二 加速与减速的加速度
1、审视速度的变化 △v
（1）表达式: △v ＝ vt－v0
若vt>v0，则△v ____0，
物体做_______运动；
若vt物体做_______运动。
二 加速与减速的加速度
1、审视速度的变化 △v
（1）表达式 △v ＝ vt－v0
（2）作图法寻找 △v
Δ
v
v0
vt
Δ
v
v0
vt
体会： △v 也有方向，
正负号的含义
二 加速与减速的加速度
1、审视速度的变化 △v
（1）表达式 △v ＝ vt－v0
（2）作图法寻找 △v
（3）再看加速度 (a = △v/ △t )
① 加速运动，a ___ 0
② 减速运动，a ___ 0
﹥
﹤
二 加速与减速的加速度
2、加速度是____量
① 加速运动，a的方向____________
② 减速运动，a的方向____________
3、匀变速直线运动：_____不变的运动
矢
运动方向相同
运动方向相反
a
⑴速度大，加速度不一定大；
加速度大, 速度不一定大。
⑵加速度为零，速度不一定为零;
速度为零，加速度也不一定为零
1、加速度和速度的区别
①它们的含义不同
速度描述的是位置变化的快慢
加速度描述的是速度变化的快慢
②看它们的大小情况
加速度大小和速度大小没必然联系；但 若a不为零，V一定变化
飞机和子弹
加速度 a = ( vt - v0 ) / t
2、加速度和速度的变化量
所以：速度变化量大，加速度不一定大;
速度的变化量Δv = vt - vo
加速度是速度对时间的 变化率
a 与Δv 也无直接联系，但a与Δv 的方向一致。
初速度
m/s 末速度
m/s 时间
s 速度变化量
m/s 加速度
m/s2
2 5 3 3
5 2 3 -3
5 -7 3 -12
1
-1
-4
当速度增加时，加速度方向和初速度方向相同。
当速度减少时，加速度方向和初速度方向相反。
例2、足球以水平速度V0=10m/s击中球门横梁后以v=8m/s的速度水平弹回，与横梁接触的时间为0.1s，求足球在此过程中的加速度。
解：设初速度为正方向则：V0=10m/s V=-8m/s t=0.1S
根据：
=(-8m/s-10m/s )/0.1S=-180m/s2
即足球的加速度大小为180/s2，方向与V0相反。
△v
a= ——
△t
v – v0
= ———
t
【注意】
1、在运算中必须规定正方向，通常以初速方向为正方向。则与正方向同向的物理量取为正，与正方向相反的物理量取为负。
2、速度变化量Δv=v-v0的运算一定是末速v减去初速v。。
3、要注意分析加速度的方向及计算结果中的正、负符号的物理意义。
问题讨论：
例1、下列说法正确的是：（ ）
A.加速度是物体增加的速度
B.加速度反映速度变化的大小
C.加速度反映速度变化的快慢
D.加速度的方向不能由速度方向确定，要由速度变化的方向来确定
CD
问题2、关于速度和加速度的关系，下列说法正确的是：( )
A.速度变化的越多，加速度就越大
B.速度变化的越快，加速度就越大
C.加速度方向保持不变，速度方向也保持不变
D.加速度大小不断变小，速度大小也不断变小
问题3、关于速度和加速度的关系，下列说法正确的是？( )
A.物体的速度大，加速度就大
B.物体的速度改变量大，加速度就大
C.物体在单位时间内速度变化大，加速度就大
D.物体的速度为零时，加速度必为零
B
C
问题1：下列所描述的运动中，可能的有？（ ）
A.速度变化很大，加速度很小
B.速度变化方向为正，加速度方向为负
C.速度变化越来越快，加速度越来越小
D.速度越来越大，加速度越来越小
问题讨论5：
1、有可能出现速度大，加速度小的情况吗？
2、有可能出现速度变化量小，而加速度大的情况吗？
3、有可能出现速度与加速度相反的情况吗？
4、有可能出现加速度方向与速度变化量方向相反的情况吗？
5、有可能出现加速度增大而速度减小的情况吗？
AD
如果遇到紧急情况刹车，2s内速度从25m/s减为零，这个过程也是匀变速的，求这个过程中的加速度。
课堂练习1
解：设初速度为正方向则：V0=25m/s V=0m/s t=2S
根据：
=(0m/s-25m/s )/2S=-12.5m/s2
这个过程的加速度大小为12.5/s2，方向与V0相反。
△v
a= ——
△t
v – v0
= ———
t
三、从 v-t 图象看加速度
t/s
思考与讨论：图中两条直线a、b分别是两个物体运动的速度一时间图象，哪个物体运动的加速度比较大
V-t 图像的斜率(陡,缓)就是加速度
△va
aa= ——
△ta
△vb
ab= ——
△tb
>
t/s
5
10
15
20
25
0
20
40
60
80
v/(m s-1)
甲
乙
例3：由速度时间图象求加速度
方向与初速度方向相同
方向与初速度方向相反
O
v/m·s-1
t/s
4
6
2
4
6
2
1、前2秒内的加速度
2、2s—4s的加速度
3、4s—6s的加速度
练习2：请根据图象求下列问题
解：
1、α=(4-1)/2 m/s2 =1.5 m/s2
2、匀速直线运动： α=0
3、α=(0-4)/（6-4） m/s2
=-2m/s2
课堂小结：
速度的改变量
速度
加速度
表示运动的快慢
表示速度的变化
表示速度变化的快慢
v
Δv＝v－v0
1、定义：速度的改变量跟发生这一改变所用的时间的比值
2、公式：
4、矢量性:加速度的方向与速度变化的方向相同
3、单位：m/s
2
4、布置作业：
P291、3、4