江苏省常州市2021-2022学年九年级数学苏科版上册 2.2圆的对称性(夯实基础) (word版含解析)
文档属性
| 名称 | 江苏省常州市2021-2022学年九年级数学苏科版上册 2.2圆的对称性(夯实基础) (word版含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 949.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-18 00:00:00 | ||
图片预览


文档简介
2.2圆的对称性(夯实基础)
一.选择题(共12小题)
1.往直径为52cm的圆柱形容器内装入一些水以后,截面如图所示,若水面宽AB=48cm,则水的最大深度为( )
A.8cm
B.10cm
C.16cm
D.20cm
2.如图,在半径为3的⊙O中,AB是直径,AC是弦,D是的中点,AC与BD交于点E.若E是BD的中点,则AC的长是( )
A.
B.3
C.3
D.4
3.如图,⊙O的直径CD=20,AB是⊙O的弦,AB⊥CD,垂足为M,OM:OC=3:5,则AB的长为( )
A.8
B.12
C.16
D.2
4.如图,一条公路的转弯处是一段圆弧(),点O是这段弧所在圆的圆心,AB=40m,点C是的中点,点D是AB的中点,且CD=10m,则这段弯路所在圆的半径为( )
A.25m
B.24m
C.30m
D.60m
第1题
第2题
第3题
第4题
第5题
第6题
5.如图所示A、B、C、D四点在⊙O上的位置,其中=180°,且=,=.若阿超在上取一点P,在上取一点Q,使得∠APQ=130°,则下列叙述何者正确?( )
A.Q点在上,且>
B.Q点在上,且<
C.Q点在上,且>
D.Q点在上,且<
6.如图,AC是⊙O的直径,弦BD⊥AO于E,连接BC,过点O作OF⊥BC于F,若BD=8cm,AE=2cm,则OF的长度是( )
A.3cm
B.cm
C.2.5cm
D.cm
7.如图,AB是⊙O的直径,弦CD交AB于点P,AP=2,BP=6,∠APC=30°,则CD的长为( )
A.
B.2
C.2
D.8
8.如图,⊙O的半径OA=6,以A为圆心,OA为半径的弧交⊙O于B、C点,则BC=( )
A.
B.
C.
D.
9.已知AB,CD是⊙O的两条平行弦,AB=8,CD=6,⊙O的半径为5,则弦AB与CD的距离为( )
A.1
B.7
C.4或3
D.7或1
10.点A、C为半径是3的圆周上两点,点B为的中点,以线段BA、BC为邻边作菱形ABCD,顶点D恰在该圆直径的三等分点上,则该菱形的边长为( )
A.或2
B.或2
C.或2
D.或2
11.如图,CD为⊙O的直径,弦AB⊥CD,垂足为M,若AB=12,OM:MD=5:8,则⊙O的周长为( )
A.26π
B.13π
C.
D.
第7题
第8题
第11题
第12题
第13题
12.如图,已知⊙O的半径OB为3,且CD⊥AB,∠D=15°.则OE的长为( )
A.
B.
C.
D.3
二.填空题(共12小题)
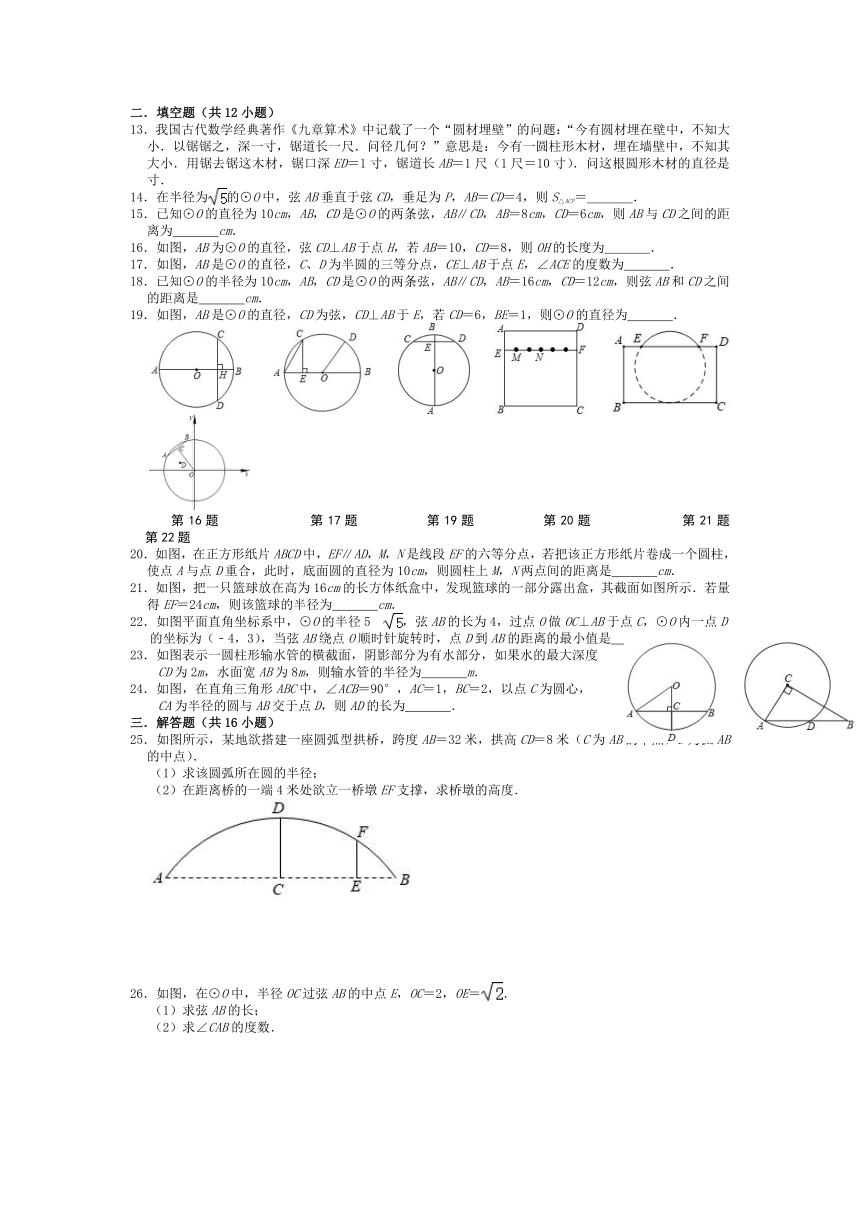
13.我国古代数学经典著作《九章算术》中记载了一个“圆材埋壁”的问题:“今有圆材埋在壁中,不知大小.以锯锯之,深一寸,锯道长一尺.问径几何?”意思是:今有一圆柱形木材,埋在墙壁中,不知其大小.用锯去锯这木材,锯口深ED=1寸,锯道长AB=1尺(1尺=10寸).问这根圆形木材的直径是
寸.
14.在半径为的⊙O中,弦AB垂直于弦CD,垂足为P,AB=CD=4,则S△ACP=
.
15.已知⊙O的直径为10cm,AB,CD是⊙O的两条弦,AB∥CD,AB=8cm,CD=6cm,则AB与CD之间的距离为
cm.
16.如图,AB为⊙O的直径,弦CD⊥AB于点H,若AB=10,CD=8,则OH的长度为
.
17.如图,AB是⊙O的直径,C、D为半圆的三等分点,CE⊥AB于点E,∠ACE的度数为
.
18.已知⊙O的半径为10cm,AB,CD是⊙O的两条弦,AB∥CD,AB=16cm,CD=12cm,则弦AB和CD之间的距离是
cm.
19.如图,AB是⊙O的直径,CD为弦,CD⊥AB于E,若CD=6,BE=1,则⊙O的直径为
.
第16题
第17题
第19题
第20题
第21题
第22题
20.如图,在正方形纸片ABCD中,EF∥AD,M,N是线段EF的六等分点,若把该正方形纸片卷成一个圆柱,使点A与点D重合,此时,底面圆的直径为10cm,则圆柱上M,N两点间的距离是
cm.
21.如图,把一只篮球放在高为16cm的长方体纸盒中,发现篮球的一部分露出盒,其截面如图所示.若量得EF=24cm,则该篮球的半径为
cm.
22.如图平面直角坐标系中,⊙O的半径5?,弦AB的长为4,过点O做OC⊥AB于点C,⊙O内一点D的坐标为(﹣4,3),当弦AB绕点O顺时针旋转时,点D到AB的距离的最小值是
.
23.如图表示一圆柱形输水管的横截面,阴影部分为有水部分,如果水的最大深度
CD为2m,水面宽AB为8m,则输水管的半径为
m.
24.如图,在直角三角形ABC中,∠ACB=90°,AC=1,BC=2,以点C为圆心,
CA为半径的圆与AB交于点D,则AD的长为
.
三.解答题(共16小题)
25.如图所示,某地欲搭建一座圆弧型拱桥,跨度AB=32米,拱高CD=8米(C为AB的中点,D为弧AB的中点).
(1)求该圆弧所在圆的半径;
(2)在距离桥的一端4米处欲立一桥墩EF支撑,求桥墩的高度.
26.如图,在⊙O中,半径OC过弦AB的中点E,OC=2,OE=.
(1)求弦AB的长;
(2)求∠CAB的度数.
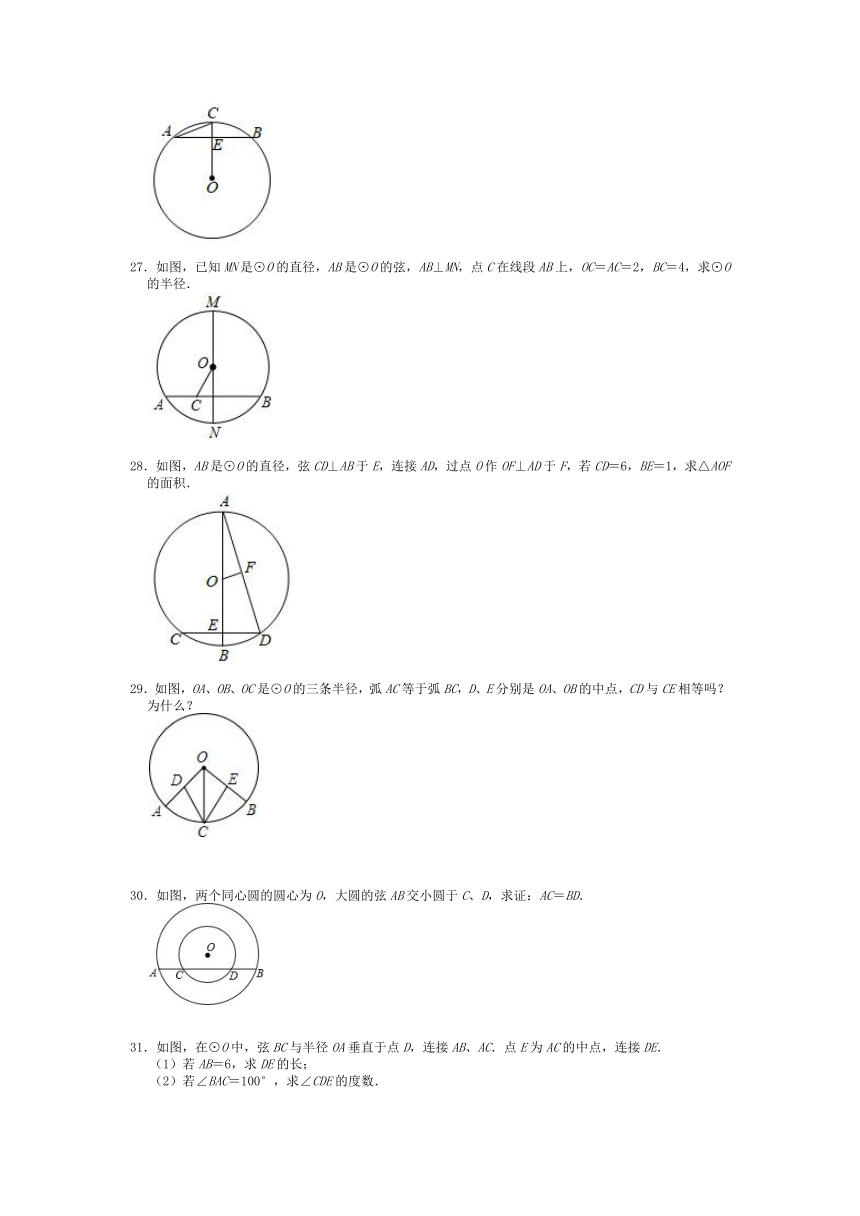
27.如图,已知MN是⊙O的直径,AB是⊙O的弦,AB⊥MN,点C在线段AB上,OC=AC=2,BC=4,求⊙O的半径.
28.如图,AB是⊙O的直径,弦CD⊥AB于E,连接AD,过点O作OF⊥AD于F,若CD=6,BE=1,求△AOF的面积.
29.如图,OA、OB、OC是⊙O的三条半径,弧AC等于弧BC,D、E分别是OA、OB的中点,CD与CE相等吗?为什么?
30.如图,两个同心圆的圆心为O,大圆的弦AB交小圆于C、D,求证:AC=BD.
31.如图,在⊙O中,弦BC与半径OA垂直于点D,连接AB、AC.点E为AC的中点,连接DE.
(1)若AB=6,求DE的长;
(2)若∠BAC=100°,求∠CDE的度数.
32.如图,已知圆O的直径AB垂直于弦CD于点E,连接CO并延长交AD于点F,且CF⊥AD.
(1)证明:点E是OB的中点;
(2)若AE=8,求CD的长.
33.如图,MB,MD是⊙O的两条弦,点A,C分别在弧MB,弧MD上,且AB=CD,点M是弧AC的中点.
(1)求证:MB=MD;
(2)过O作OE⊥MB于E,OE=1,⊙O的半径是2,求MD的长.
34.《九章算术》是我国古代著名数学经典,其中对勾股定理的论述比西方早一千多年,其中有这样一个问题:“今有圆材埋在壁中,不知大小:以锯锯之,深一寸,锯道长一尺.问径几何?”其意为:今有一圆柱形木材,埋在墙壁中,不知其大小,用锯去锯该材料,锯口深1寸,锯道长1尺.如图,已知弦AB=1尺,弓形高CD=1寸,(注:1尺=10寸)问这块圆柱形木材的直径是多少寸?
35.如图,某石拱桥的桥拱是圆弧形,拱的跨度AB为24m,点O是所在圆的圆心,⊙O的半径为13m,求桥拱的高度.(弧的中点到弦的距离)
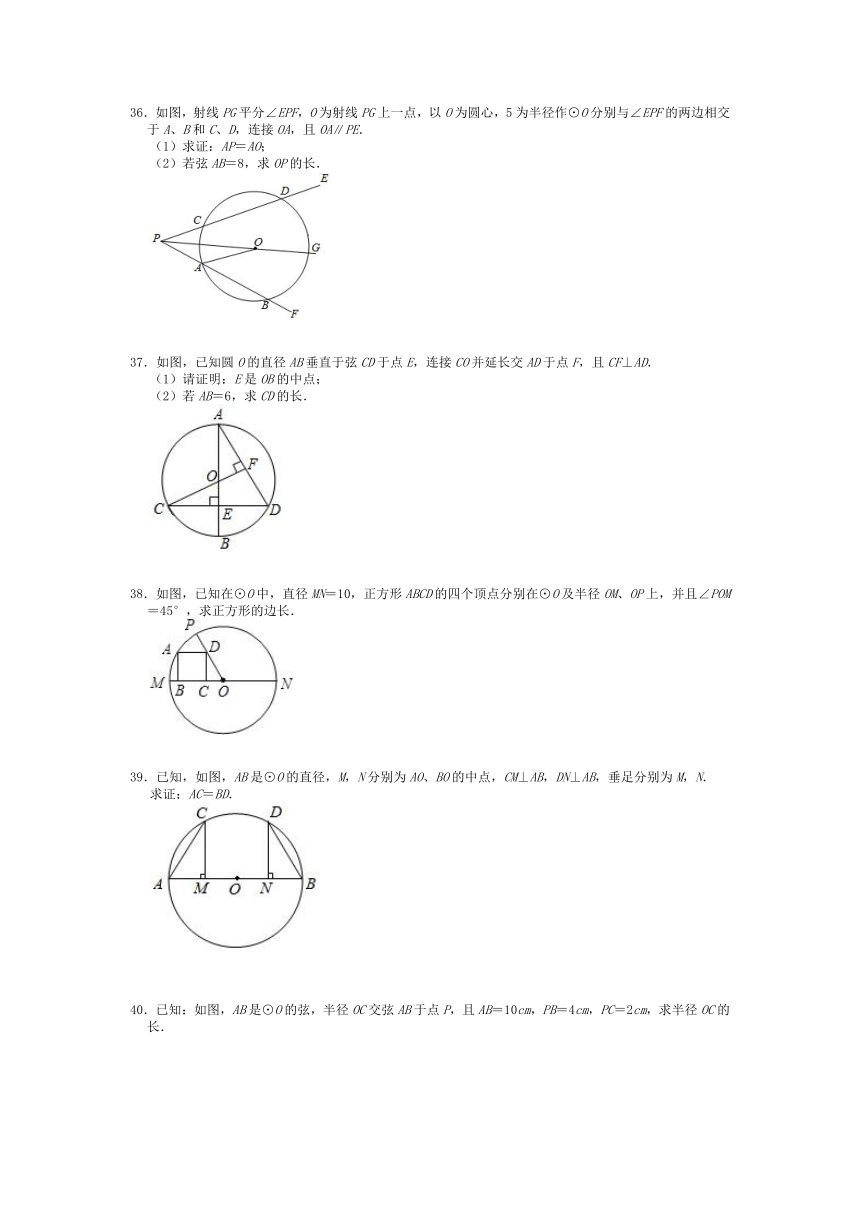
36.如图,射线PG平分∠EPF,O为射线PG上一点,以O为圆心,5为半径作⊙O分别与∠EPF的两边相交于A、B和C、D,连接OA,且OA∥PE.
(1)求证:AP=AO;
(2)若弦AB=8,求OP的长.
37.如图,已知圆O的直径AB垂直于弦CD于点E,连接CO并延长交AD于点F,且CF⊥AD.
(1)请证明:E是OB的中点;
(2)若AB=6,求CD的长.
38.如图,已知在⊙O中,直径MN=10,正方形ABCD的四个顶点分别在⊙O及半径OM、OP上,并且∠POM=45°,求正方形的边长.
39.已知,如图,AB是⊙O的直径,M,N分别为AO、BO的中点,CM⊥AB,DN⊥AB,垂足分别为M,N.
求证:AC=BD.
40.已知:如图,AB是⊙O的弦,半径OC交弦AB于点P,且AB=10cm,PB=4cm,PC=2cm,求半径OC的长.
2.2圆的对称性(夯实基础)
参考答案与试题解析
一.选择题(共12小题)
1.往直径为52cm的圆柱形容器内装入一些水以后,截面如图所示,若水面宽AB=48cm,则水的最大深度为( )
A.8cm
B.10cm
C.16cm
D.20cm
【分析】连接OB,过点O作OC⊥AB于点D,交⊙O于点C,先由垂径定理求出BD的长,再根据勾股定理求出OD的长,进而可得出CD的长.
【解答】解:连接OB,过点O作OC⊥AB于点D,交⊙O于点C,如图所示:
∵AB=48cm,
∴BD=AB=×48=24(cm),
∵⊙O的直径为52cm,
∴OB=OC=26cm,
在Rt△OBD中,OD===10(cm),
∴CD=OC﹣OD=26﹣10=16(cm),
故选:C.
【点评】本题考查了垂径定理、勾股定理等知识;根据题意作出辅助线,构造出直角三角形是解答此题的关键.
2.如图,在半径为3的⊙O中,AB是直径,AC是弦,D是的中点,AC与BD交于点E.若E是BD的中点,则AC的长是( )
A.
B.3
C.3
D.4
【分析】连接OD,交AC于F,根据垂径定理得出OD⊥AC,AF=CF,进而证得DF=BC,根据三角形中位线定理求得OF=BC=DF,从而求得BC=DF=2,利用勾股定理即可求得AC.
【解答】解:连接OD,交AC于F,
∵D是的中点,
∴OD⊥AC,AF=CF,
∴∠DFE=90°,
∵OA=OB,AF=CF,
∴OF=BC,
∵AB是直径,
∴∠ACB=90°,
在△EFD和△ECB中
∴△EFD≌△ECB(AAS),
∴DF=BC,
∴OF=DF,
∵OD=3,
∴OF=1,
∴BC=2,
在Rt△ABC中,AC2=AB2﹣BC2,
∴AC===4,
故选:D.
【点评】本题考查了垂径定理,三角形全等的判定和性质,三角形中位线定理,熟练掌握性质定理是解题的关键.
3.如图,⊙O的直径CD=20,AB是⊙O的弦,AB⊥CD,垂足为M,OM:OC=3:5,则AB的长为( )
A.8
B.12
C.16
D.2
【分析】连接OA,先根据⊙O的直径CD=20,OM:OC=3:5求出OD及OM的长,再根据勾股定理可求出AM的长,进而得出结论.
【解答】解:连接OA,
∵⊙O的直径CD=20,OM:OC=3:5,
∴OC=10,OM=6,
∵AB⊥CD,
∴AM===8,
∴AB=2AM=16.
故选:C.
【点评】本题考查的是垂径定理,根据题意作出辅助线,构造出直角三角形是解答此题的关键.
4.如图,一条公路的转弯处是一段圆弧(),点O是这段弧所在圆的圆心,AB=40m,点C是的中点,点D是AB的中点,且CD=10m,则这段弯路所在圆的半径为( )
A.25m
B.24m
C.30m
D.60m
【分析】根据题意,可以推出AD=BD=20,若设半径为r,则OD=r﹣10,OB=r,结合勾股定理可推出半径r的值.
【解答】解:∵OC⊥AB,
∴AD=DB=20m,
在Rt△AOD中,OA2=OD2+AD2,
设半径为r得:r2=(r﹣10)2+202,
解得:r=25m,
∴这段弯路的半径为25m
故选:A.
【点评】本题主要考查垂径定理的应用、勾股定理的应用,关键在于设出半径为r后,用r表示出OD、OB的长度.
5.如图所示A、B、C、D四点在⊙O上的位置,其中=180°,且=,=.若阿超在上取一点P,在上取一点Q,使得∠APQ=130°,则下列叙述何者正确?( )
A.Q点在上,且>
B.Q点在上,且<
C.Q点在上,且>
D.Q点在上,且<
【分析】连接AD,OB,OC,根据题意得到∠BOC=∠DOC=45°,在圆周上取一点E连接AE,CE,由圆周角定理得到∠E=AOC=67.5°,求得∠ABC=112.5°<130°,取的中点F,连接OF,得到∠ABF=123.25°<130°,于是得到结论.
【解答】解:连接AD,OB,OC,
∵=180°,且=,=,
∴∠BOC=∠DOC=45°,
在圆周上取一点E连接AE,CE,
∴∠E=AOC=67.5°,
∴∠ABC=112.5°<130°,
取的中点F,连接OF,
则∠AOF=∠AOB+∠BOF=90°+22.5°=112.5°,
∴∠ABF=∠ABO+∠OBF=45°+(180°﹣22.5°)=123.75°<130°,
∴Q点在上,且<,
故选:B.
【点评】本题考查了圆心角,弧,弦的关系,圆内接四边形的性质,圆周角定理,正确的理解题意是解题的关键.
6.如图,AC是⊙O的直径,弦BD⊥AO于E,连接BC,过点O作OF⊥BC于F,若BD=8cm,AE=2cm,则OF的长度是( )
A.3cm
B.cm
C.2.5cm
D.cm
【分析】根据垂径定理得出AB的长,进而利用中位线定理得出OF即可.
【解答】解:连接AB,OB,
∵AC是⊙O的直径,弦BD⊥AO于E,BD=8cm,AE=2cm,
在Rt△ABE中,AE2+BE2=AB2,
即AB=,
∵OA=OC,OB=OC,OF⊥BC,
∴BF=FC,
∴OF=.
故选:D.
【点评】此题考查垂径定理,关键是根据垂径定理得出OE的长.
7.如图,AB是⊙O的直径,弦CD交AB于点P,AP=2,BP=6,∠APC=30°,则CD的长为( )
A.
B.2
C.2
D.8
【分析】作OH⊥CD于H,连接OC,如图,根据垂径定理由OH⊥CD得到HC=HD,再利用AP=2,BP=6可计算出半径OA=4,则OP=OA﹣AP=2,接着在Rt△OPH中根据含30度的直角三角形的性质计算出OH=OP=1,然后在Rt△OHC中利用勾股定理计算出CH=,所以CD=2CH=2.
【解答】解:作OH⊥CD于H,连接OC,如图,
∵OH⊥CD,
∴HC=HD,
∵AP=2,BP=6,
∴AB=8,
∴OA=4,
∴OP=OA﹣AP=2,
在Rt△OPH中,∵∠OPH=30°,
∴∠POH=60°,
∴OH=OP=1,
在Rt△OHC中,∵OC=4,OH=1,
∴CH==,
∴CD=2CH=2.
故选:C.
【点评】本题考查了垂径定理:垂直于弦的直径平分这条弦,并且平分弦所对的两条弧.也考查了勾股定理以及含30度的直角三角形的性质.
8.如图,⊙O的半径OA=6,以A为圆心,OA为半径的弧交⊙O于B、C点,则BC=( )
A.
B.
C.
D.
【分析】根据垂径定理先求BC一半的长,再求BC的长.
【解答】解:设OA与BC相交于D点.
∵AB=OA=OB=6
∴△OAB是等边三角形.
又根据垂径定理可得,OA平分BC,
利用勾股定理可得BD==3
所以BC=6.
故选:A.
【点评】本题的关键是利用垂径定理和勾股定理.
9.已知AB,CD是⊙O的两条平行弦,AB=8,CD=6,⊙O的半径为5,则弦AB与CD的距离为( )
A.1
B.7
C.4或3
D.7或1
【分析】连接OC、OA,作直线OF⊥AB于E,交CD于F,则EF⊥CD,根据垂径定理求出CF,AE,根据勾股定理求出OE、OF,即可得出答案.
【解答】解:如图所示,连接OA,OC.作直线OF⊥AB于E,交CD于F,则EF⊥CD,
∵OE⊥AB,OF⊥CD,
∴AE=AB=4,CF=CD=3,
根据勾股定理,得
OE==3,OF==4,
所以当AB和CD在圆心的同侧时,则EF=OF﹣OE=1,
当AB和CD在圆心的异侧时,则EF=OF+OE=7.
故选:D.
【点评】本题考查了垂径定理的知识,此题综合运用了垂径定理和勾股定理,特别注意有时要考虑两种情况.
10.点A、C为半径是3的圆周上两点,点B为的中点,以线段BA、BC为邻边作菱形ABCD,顶点D恰在该圆直径的三等分点上,则该菱形的边长为( )
A.或2
B.或2
C.或2
D.或2
【分析】过B作直径,连接AC交BO于E,如图①,根据已知条件得到BD=×2×3=2,如图②,BD=×2×3=4,求得OD=1,OE=2,DE=1,连接OD,根据勾股定理得到结论,
【解答】解:过B作直径,连接AC交BO于E,
∵点B为的中点,
∴BD⊥AC,
如图①,
∵点D恰在该圆直径的三等分点上,
∴BD=×2×3=2,
∴OD=OB﹣BD=1,
∵四边形ABCD是菱形,
∴DE=BD=1,
∴OE=2,
连接OC,
∵CE==,
∴边CD==;
如图②,BD=×2×3=4,
同理可得,OD=1,OE=1,DE=2,
连接OC,
∵CE===2,
∴边CD===2,
故选:D.
【点评】本题考查了圆心角,弧,弦的关系,勾股定理,菱形的性质,正确的作出图形是解题的关键.
11.如图,CD为⊙O的直径,弦AB⊥CD,垂足为M,若AB=12,OM:MD=5:8,则⊙O的周长为( )
A.26π
B.13π
C.
D.
【分析】连接OA,根据垂径定理得到AM=AB=6,设OM=5x,DM=8x,得到OA=OD=13x,根据勾股定理得到OA=×13,于是得到结论.
【解答】解:连接OA,
∵CD为⊙O的直径,弦AB⊥CD,
∴AM=AB=6,
∵OM:MD=5:8,
∴设OM=5x,DM=8x,
∴OA=OD=13x,
∴AM=12x=6,
∴x=,
∴OA=×13,
∴⊙O的周长=2OA?π=13π,
故选:B.
【点评】本题考查的是垂径定理,根据题意作出辅助线,构造出直角三角形,利用勾股定理求解是解答此题的关键.
12.如图,已知⊙O的半径OB为3,且CD⊥AB,∠D=15°.则OE的长为( )
A.
B.
C.
D.3
【分析】连接OA,先根据圆O的直径为6求出OA的长,再由CD⊥AB得出∠AEO=90°,由圆周角定理求出∠AOE的度数,根据直角三角形的性质即可得出结论.
【解答】解:连接OA,
∵圆O的直径为6,
∴OA=3.
∵CD⊥AB,
∴∠AEO=90°.
∵∠D=15°,
∴∠AOE=30°,
∴OE=OA?cos30°=3×=.
故选:A.
【点评】本题考查的是垂径定理,熟知平分弦的直径平分这条弦,并且平分弦所对的两条弧是解答此题的关键.
二.填空题(共12小题)
13.我国古代数学经典著作《九章算术》中记载了一个“圆材埋壁”的问题:“今有圆材埋在壁中,不知大小.以锯锯之,深一寸,锯道长一尺.问径几何?”意思是:今有一圆柱形木材,埋在墙壁中,不知其大小.用锯去锯这木材,锯口深ED=1寸,锯道长AB=1尺(1尺=10寸).问这根圆形木材的直径是 26 寸.
【分析】根据题意可得OE⊥AB,由垂径定理可得尺=5寸,设半径OA=OE=r寸,则OD=r﹣1,在Rt△OAD中,根据勾股定理可得:(r﹣1)2+52=r2,解方程可得出木材半径,即可得出木材直径.
【解答】解:由题意可知OE⊥AB,
∵OE为⊙O半径,
∴尺=5寸,
设半径OA=OE=r寸,
∵ED=1,
∴OD=r﹣1,
则Rt△OAD中,根据勾股定理可得:(r﹣1)2+52=r2,
解得:r=13,
∴木材直径为26寸;
故答案为:26.
【点评】本题考查垂径定理结合勾股定理计算半径长度.如果题干中出现弦的垂线或者弦的中点,则可验证是否满足垂径定理;与圆有关的题目中如果求弦长或者求半径直径,也可以从题中寻找是否有垂径定理,然后构造直角三角形,用勾股定理求解.
14.在半径为的⊙O中,弦AB垂直于弦CD,垂足为P,AB=CD=4,则S△ACP= 或或 .
【分析】如图1,作OE⊥AB于E,OF⊥CD于F,连接OD、OB,如图,根据垂径定理得到AE=BE=AB=2,DF=CF=CD=2,根据勾股定理在Rt△OBE中计算出OE=1,同理可得OF=1,接着证明四边形OEPF为正方形,于是得到PA=PC=1,根据三角形面积公式求得即可.
【解答】解:作OE⊥AB于E,OF⊥CD于F,连接OD、OB,
则AE=BE=AB=2,DF=CF=CD=2,
如图1,
在Rt△OBE中,∵OB=,BE=2,
∴OE==1,
同理可得OF=1,
∵AB⊥CD,
∴四边形OEPF为矩形,
∴PE=PF=1,
∴PA=PC=1,
∴S△APC==;
如图2,
同理:S△APC==;
如图3,
同理:S△APC==;
故答案为:或或.
【点评】本题考查了垂径定理:垂直于弦的直径平分这条弦,并且平分弦所对的两条弧.也考查了勾股定理.
15.已知⊙O的直径为10cm,AB,CD是⊙O的两条弦,AB∥CD,AB=8cm,CD=6cm,则AB与CD之间的距离为 1或7 cm.
【分析】作OE⊥AB于E,延长EO交CD于F,连接OA、OC,如图,利用平行线的性质OF⊥CD,根据垂径定理得到AE=BE=4,CF=DF=3,则利用勾股定理可计算出OE=3,OF=4,讨论:当点O在AB与CD之间时,EF=OF+OE;当点O不在AB与CD之间时,EF=OF﹣OE.
【解答】解:作OE⊥AB于E,延长EO交CD于F,连接OA、OC,如图,
∵AB∥CD,OE⊥AB,
∴OF⊥CD,
∴AE=BE=AB=4cm,CF=DF=CD=3cm,
在Rt△OAE中,OE===3cm,
在Rt△OCF中,OF===4cm,
当点O在AB与CD之间时,如图1,EF=OF+OE=4+3=7cm;
当点O不在AB与CD之间时,如图2,EF=OF﹣OE=4﹣3=1cm;
综上所述,AB与CD之间的距离为1cm或7cm.
故答案为1或7.
【点评】本题考查了垂径定理:垂直于弦的直径平分这条弦,并且平分弦所对的两条弧.注意分类讨论.
16.如图,AB为⊙O的直径,弦CD⊥AB于点H,若AB=10,CD=8,则OH的长度为 3 .
【分析】根据垂径定理由CD⊥AB得到CH=CD=4,再根据勾股定理计算出OH=3.
【解答】解:连接OC,
∵CD⊥AB,
∴CH=DH=CD=×8=4,
∵直径AB=10,
∴OC=5,
在Rt△OCH中,OH==3,
故答案为:3.
【点评】本题考查了垂径定理:垂直于弦的直径平分这条弦,并且平分弦所对的两条弧.
17.如图,AB是⊙O的直径,C、D为半圆的三等分点,CE⊥AB于点E,∠ACE的度数为 30° .
【分析】想办法证明△AOC是等边三角形即可解决问题.
【解答】解:如图,连接OC.
∵AB是直径,==,
∴∠AOC=∠COD=∠DOB=60°,
∵OA=OC,
∴△AOC是等边三角形,
∴∠A=60°,
∵CE⊥OA,
∴∠AEC=90°,
∴∠ACE=90°﹣60°=30°.
故答案为30°
【点评】本题考查等弧所对的圆心角相等的性质、等边三角形的判定和性质等知识,解题的关键是熟练掌握基本知识,属于中考常考题型.
18.已知⊙O的半径为10cm,AB,CD是⊙O的两条弦,AB∥CD,AB=16cm,CD=12cm,则弦AB和CD之间的距离是 2或14 cm.
【分析】分两种情况进行讨论:①弦AB和CD在圆心同侧;②弦AB和CD在圆心异侧;作出半径和弦心距,利用勾股定理和垂径定理求解即可,小心别漏解.
【解答】解:①当弦AB和CD在圆心同侧时,如图,
∵AB=16cm,CD=12cm,
∴AE=8cm,CF=6cm,
∵OA=OC=10cm,
∴EO=6cm,OF=8cm,
∴EF=OF﹣OE=2cm;
②当弦AB和CD在圆心异侧时,如图,
∵AB=16cm,CD=12cm,
∴AF=8cm,CE=6cm,
∵OA=OC=10cm,
∴OF=6cm,OE=8cm,
∴EF=OF+OE=14cm.
∴AB与CD之间的距离为14cm或2cm.
故答案为:2或14.
【点评】本题考查了勾股定理和垂径定理的应用.此题难度适中,解题的关键是注意掌握数形结合思想与分类讨论思想的应用,小心别漏解.
19.
如图,AB是⊙O的直径,CD为弦,CD⊥AB于E,若CD=6,BE=1,则⊙O的直径为 10 .
【分析】首先连接OD,并设OD=x,然后在△ODE中,由勾股定理,求出OD的长,即可求出⊙O的直径为多少.
【解答】解:如图,连接OD,设OD=x,,
∵AB是⊙O的直径,而且CD⊥AB于E,
∴DE=CE=6÷2=3,
在Rt△ODE中,
x2=(x﹣1)2+32,
解得x=5,
∵5×2=10,
∴⊙O的直径为10.
故答案为:10.
【点评】此题主要考查了垂径定理以及勾股定理的应用,要熟练掌握,解答此题的关键是求出OD的长度是多少.
20.如图,在正方形纸片ABCD中,EF∥AD,M,N是线段EF的六等分点,若把该正方形纸片卷成一个圆柱,使点A与点D重合,此时,底面圆的直径为10cm,则圆柱上M,N两点间的距离是 5 cm.
【分析】根据题意得到MN=BC,当正方形纸片卷成一个圆柱时,EF卷成一个圆,线段卷成圆上一段弧,该段弧所对的圆心角为×360°,要求圆柱上M,N两点间的距离即求弦MN的长.
【解答】解:根据题意得:EF=AD=BC,MN=2EM=EF,
把该正方形纸片卷成一个圆柱,使点A与点D重合,则线段EF形成一直径为10cm的圆,线段EF为圆上的一段弧.
所对的圆心角为:×360°=120°,
所以圆柱上M,N两点间的距离为:2×5×sin60°=5cm.
故答案为:5.
【点评】此题实质考查了圆上弦的计算,需要先找出圆心角再根据弦长公式计算,熟练掌握公式及性质是解本题的关键.
21.如图,把一只篮球放在高为16cm的长方体纸盒中,发现篮球的一部分露出盒,其截面如图所示.若量得EF=24cm,则该篮球的半径为 12.5 cm.
【分析】取EF的中点M,作MN⊥AD于点M,取MN上的球心O,连接OF,设OF=x,则OM=16﹣x,MF=12,在Rt△MOF中利用勾股定理求得OF的长即可.
【解答】解:EF的中点M,作MN⊥AD于点M,取MN上的球心O,连接OF,
∵四边形ABCD是矩形,
∴∠C=∠D=90°,
∴四边形CDMN是矩形,
∴MN=CD=16cm,
设OF=xcm,则ON=OF,
∴OM=MN﹣ON=16﹣x,MF=12cm,
在直角三角形OMF中,OM2+MF2=OF2
即:(16﹣x)2+122=x2
解得:x=12.5(cm),
故答案为:12.5.
【点评】本题主考查垂径定理、矩形的性质及勾股定理的应用,正确作出辅助线构造直角三角形是解题的关键.
22.如图平面直角坐标系中,⊙O的半径5?,弦AB的长为4,过点O做OC⊥AB于点C,⊙O内一点D的坐标为(﹣4,3),当弦AB绕点O顺时针旋转时,点D到AB的距离的最小值是 6 .
【分析】连接OB,如图,利用垂径定理得到AC=BC=2,则利用勾股定理可计算出OC=11,利用垂线段最短,当OC经过点D时,点D到AB的距离的最小,然后计算出OD的长,从而得到点D到AB的距离的最小值.
【解答】解:连接OB,如图,
∵OC⊥AB,
∴AC=BC=AB=2,
在Rt△OBC中,OC===11,
当OC经过点D时,点D到AB的距离的最小,
∵OD==5,
∴点D到AB的距离的最小值为11﹣5=6.
故答案为6.
【点评】本题考查了垂径定理:垂直于弦的直径平分这条弦,并且平分弦所对的两条弧.也考查了勾股定理.
23.如图表示一圆柱形输水管的横截面,阴影部分为有水部分,如果水的最大深度CD为2m,水面宽AB为8m,则输水管的半径为 5 m.
【分析】由垂径定理可知AC=4m,设OA=rm,则OC=(r﹣1)m,在Rt△AOC中,再利用勾股定理即可求出r的值.
【解答】解:由题意得:OD⊥AB,
∴AC=AB=×8=4(m),
设OA=rm,则OC=OD﹣CD=(r﹣2)m,
在Rt△AOC中,由勾股定理得:OA2=OC2+AC2,
即r2=(r﹣2)2+42,
解得:r=5,
即输水管的半径为5m,
故答案为:5.
【点评】本题考查的是垂径定理的应用及勾股定理,熟练掌握垂径定理,由勾股定理得出方程是解题的关键.
24.如图,在直角三角形ABC中,∠ACB=90°,AC=1,BC=2,以点C为圆心,CA为半径的圆与AB交于点D,则AD的长为 .
【分析】作CE⊥AB于E,根据勾股定理得到AB=,利用三角形面积公式求出CE,根据勾股定理求出AE,根据垂径定理计算即可.
【解答】解:作CE⊥AB于E,
则AE=AD,
∵∠ACB=90°,AC=1,BC=2,
∴AB==,
×AB×CE=AC×BC,即×CE=,
解得,CE=,
AE==,
则AD=2AE=,
故答案为:.
【点评】本题考查的是勾股定理和垂径定理的应用,垂径定理:垂直弦的直径平分这条弦,并且平分弦所对的两条弧.
三.解答题(共16小题)
25.如图所示,某地欲搭建一座圆弧型拱桥,跨度AB=32米,拱高CD=8米(C为AB的中点,D为弧AB的中点).
(1)求该圆弧所在圆的半径;
(2)在距离桥的一端4米处欲立一桥墩EF支撑,求桥墩的高度.
【分析】(1)设弧AB所在的圆心为O,C为弧AB的中点,CD⊥AB于D,延长CD经过O点,设⊙O的半径为R,利用勾股定理求出即可;
(2)利用垂径定理以及勾股定理得出AO的长,再求出EF的长即可.
【解答】解:(1)设弧AB所在的圆心为O,C为弧AB的中点,CD⊥AB于D,延长CD经过O点,设⊙O的半径为R,
在Rt△OBD中,OB2=OD2+DB2,
∴R2=(R﹣8)2+162,
解得R=20;
(2)在圆弧型中设点F′在弧AB上,作F′E′⊥AB于E′,
OH⊥F′E′于H,则OH=DE′=16﹣4=12,OF′=R=20,
在Rt△OHF′中,HF′=,
∵HE′=OD=OC﹣CD=20﹣8=12,E′F′=HF′﹣HE′=16﹣12=4(米),
∴在离桥的一端4米处,圆弧型桥墩高4米.
【点评】此题主要考查了垂径定理的应用,根据题意画出图形结合勾股定理得出是解题关键.
26.如图,在⊙O中,半径OC过弦AB的中点E,OC=2,OE=.
(1)求弦AB的长;
(2)求∠CAB的度数.
【分析】(1)连接OB,先由垂径定理得OC⊥AB,AE=BE,OB=OC=2,再由勾股定理求出BE=,即可求解;
(2)先证△BOE是等腰直角三角形,得∠BOC=45°,再由圆周角定理即可求解.
【解答】解:(1)连接OB,如图所示:
∵半径OC过弦AB的中点E,
∴OC⊥AB,AE=BE,OB=OC=2,
∴BE===,
∴AB=2BE=2;
(2)由(1)得:BE=OE,OC⊥AB,
∴△BOE是等腰直角三角形,
∴∠BOC=45°,
∴∠CAB=∠BOC=22.5°.
【点评】本题考查了垂径定理、勾股定理、等腰直角三角形的判定与性质以及圆周角定理等知识;熟练掌握垂径定理和勾股定理是解题的关键.
27.如图,已知MN是⊙O的直径,AB是⊙O的弦,AB⊥MN,点C在线段AB上,OC=AC=2,BC=4,求⊙O的半径.
【分析】连接OB,先由垂径定理得AD=BD=AB=3,则CD=AD﹣AC=1,再由勾股定理求出OD=,然后由勾股定理求出OB即可.
【解答】解:连接OB,设AB与MN交于点D,如图所示:
∵AC=2,BC=4,
∴AB=AC+BC=6,
∵AB⊥MN,
∴AD=BD=AB=3,∠ODC=∠ODB=90°,
∴CD=AD﹣AC=1,
∴OD===,
∴OB===2,
即⊙O的半径为2.
【点评】本题考查了垂径定理和勾股定理;熟练掌握垂径定理和勾股定理是解题的关键.
28.如图,AB是⊙O的直径,弦CD⊥AB于E,连接AD,过点O作OF⊥AD于F,若CD=6,BE=1,求△AOF的面积.
【分析】连接OD,先由垂径定理得CE=DE=CD=3,设⊙O的半径为r,则OE=r﹣1,OD=r,由勾股定理求出r=5,则OE=4,AE=9,求出S△AED=,S△OED=6,则S△AOD=S△AED﹣S△OED=,即可解决问题.
【解答】解:连接OD,如图所示:
∵CD⊥AB,
∴CE=DE=CD=3,
设⊙O的半径为r,
则OE=r﹣1,OD=r,
在Rt△ODE中,由勾股定理得:(r﹣1)2+32=r2,
解得:r=5,
∴OE=4,AE=5+4=9,
∴S△AED=AE?DE=×9×3=,S△OED=OE?DE=×4×3=6,
∴S△AOD=S△AED﹣S△OED=﹣6=,
∵OF⊥AD,OA=OD,
∴AF=DF,
∴S△AOF=S△AOD=×=.
【点评】本题考查了垂径定理、等腰三角形的性质、勾股定理、三角形面积的计算等知识;熟练掌握垂径定理和勾股定理是解题的关键.
29.如图,OA、OB、OC是⊙O的三条半径,弧AC等于弧BC,D、E分别是OA、OB的中点,CD与CE相等吗?为什么?
【分析】根据弧与圆心角的关系,可得∠AOC=∠BOC,又由D、E分别是半径OA、OB的中点,可得OD=OE,利用SAS判定△DOC≌△EOC,继而证得结论.
【解答】解:CD=CE,理由如下:
∵弧AC和弧BC相等,
∴∠AOC=∠BOC,
又∵OA=OB,D、E分别是OA、OB的中点,
∴OD=OE,
在△DOC和△EOC中,
,
∴△DOC≌△EOC(SAS),
∴CD=CE.
【点评】此题考查了弧与圆心角的关系以及全等三角形的判定与性质;证明三角形全等是解决问题的关键.
30.如图,两个同心圆的圆心为O,大圆的弦AB交小圆于C、D,求证:AC=BD.
【分析】过O作OE⊥AB于E,由垂径定理得出AE=BE,CE=DE,相减即可得出答案.
【解答】证明:
过O作OE⊥AB于E,
则OE⊥CD,
∵OE过O,
∴由垂径定理得:AE=BE,CE=DE,
∴AE﹣CE=BE﹣DE,
即AC=BD.
【点评】本题考查了垂径定理的应用,关键是作辅助线后得出AE=BE,CE=DE.
31.如图,在⊙O中,弦BC与半径OA垂直于点D,连接AB、AC.点E为AC的中点,连接DE.
(1)若AB=6,求DE的长;
(2)若∠BAC=100°,求∠CDE的度数.
【分析】(1)根据垂径定理得到=,则AC=AB=6,然后根据直角三角形斜边上的中线性质得到DE的长;
(2)利用等腰三角形的性质和三角形的内角和计算出∠C=40°,然后利用ED=EC得到∠CDE=∠C=40°.
【解答】解:(1)∵BC⊥OA,
∴=,∠ADC=90°,
∴AC=AB=6,
∵点E为AC的中点,
∴DE=AC=3;
(2)∵AB=AC,
∴∠B=∠C,
∵∠BAC=100°,
∴∠C=(180°﹣100°)=40°,
∵点E为AC的中点,
∴ED=EC,
∴∠CDE=∠C=40°.
【点评】本题考查了垂径定理:直于弦的直径平分这条弦,并且平分弦所对的两条弧.也考查了直角三角形斜边上的中线性质.
32.如图,已知圆O的直径AB垂直于弦CD于点E,连接CO并延长交AD于点F,且CF⊥AD.
(1)证明:点E是OB的中点;
(2)若AE=8,求CD的长.
【分析】(1)要证E是OB的中点,只要证OE=OB=OC,即证出∠OCE=30°即可;
(2)在直角△ACE中,根据∠CAB=30°就可以解得CE的长,进而求出CD的长.
【解答】(1)证明:连接AC,如图,
∵直径AB垂直于弦CD于点E,
∴=,
∴AC=AD,
∵过圆心O的线段CF⊥AD,
∴AF=DF,即CF是AD的中垂线,
∴AC=CD,
∴AC=AD=CD.
即△ACD是等边三角形,
∴∠FCD=30°,
在Rt△COE中,OE=OC,
∴OE=OB,
∴点E为OB的中点;
(2)解:∵△ACD是等边三角形,AB⊥CD,
∴∠CAE=30°,
∴CE=AE×tan30°=8×=,
∵直径AB垂直于弦CD于点E,
∴CD=2CE=.
【点评】本题考查垂径定理、等边三角形的判定、线段垂直平分线的性质、解直角三角形等知识,解题的关键是掌握垂直于弦的直径平分这条弦,并且平分弦所对的两条弧.
33.如图,MB,MD是⊙O的两条弦,点A,C分别在弧MB,弧MD上,且AB=CD,点M是弧AC的中点.
(1)求证:MB=MD;
(2)过O作OE⊥MB于E,OE=1,⊙O的半径是2,求MD的长.
【分析】(1)根据圆心角、弦、弧、弦心距之间的关系得出=即可;
(2)根据垂径定理,勾股定理求出ME,进而求出MB即可.
【解答】证明:(1)∵AB=CD,
∴=,
又∵点M是弧AC的中点,
∴=,
∴+=+,
即:=,
∴MB=MD;
(2)过O作OE⊥MB于E,则ME=BE,连接OM,
在Rt△MOE中,OE=1,⊙O的半径OM=2,
∴ME===,
∴MD=MB=2ME=2.
【点评】本题考查圆心角、弦、弧之间的关系,垂径定理、勾股定理等知识,掌握垂径定理、勾股定理是正确计算的前提.
34.《九章算术》是我国古代著名数学经典,其中对勾股定理的论述比西方早一千多年,其中有这样一个问题:“今有圆材埋在壁中,不知大小:以锯锯之,深一寸,锯道长一尺.问径几何?”其意为:今有一圆柱形木材,埋在墙壁中,不知其大小,用锯去锯该材料,锯口深1寸,锯道长1尺.如图,已知弦AB=1尺,弓形高CD=1寸,(注:1尺=10寸)问这块圆柱形木材的直径是多少寸?
【分析】设⊙O的半径为r.在Rt△ADO中,AD=5,OD=r﹣1,OA=r,则有r2=52+(r﹣1)2,解方程即可.
【解答】解:设⊙O的半径为r.
∵OC⊥AB,
∴AD=BD=AB=5,
在Rt△ADO中,AD=5,OD=r﹣1,OA=r,
则有:r2=52+(r﹣1)2,
解得:r=13,
∴⊙O的直径为26寸.
【点评】本题考查了垂径定理、勾股定理等知识,解题的关键是学会利用参数构建方程解决问题,属于中考常考题型.
35.如图,某石拱桥的桥拱是圆弧形,拱的跨度AB为24m,点O是所在圆的圆心,⊙O的半径为13m,求桥拱的高度.(弧的中点到弦的距离)
【分析】由垂径定理得AD=BD=×24=12(m),设CD=xm,则OD=(13﹣x)m,在Rt△AOD中,根据勾股定理得出方程,解方程即可.
【解答】解:如图所示:过O作OD⊥AB交于C,垂足为D,
则AD=BD=×24=12(m),
设CD=xm,则OD=(13﹣x)m,
根据勾股定理得:122+(13﹣x)2=132,
解得:x=8,
即桥拱的高度为8m.
【点评】本题考查了垂径定理和勾股定理等知识;熟练掌握垂径定理,由勾股定理得出方程是解题的关键.
36.如图,射线PG平分∠EPF,O为射线PG上一点,以O为圆心,5为半径作⊙O分别与∠EPF的两边相交于A、B和C、D,连接OA,且OA∥PE.
(1)求证:AP=AO;
(2)若弦AB=8,求OP的长.
【分析】(1)∠APO=∠AOP得到AP=AO;
(2)过O点作OH⊥AB于H,如图,根据垂径定理得到AH=BH=4,则可利用勾股定理可计算出OH=3,然后在Rt△POH中利用勾股定理计算OP.
【解答】(1)证明:∵PG平分∠EPF,
∴∠DPO=∠APO,
∵OA∥PE,
∴∠DPO=∠AOP,
∴∠APO=∠AOP,
∴AP=AO;
(2)解:过O点作OH⊥AB于H,如图,则AH=BH=AB=4,
在Rt△AOH中,∵OA=5,AH=4,
∴OH==3,
∵AP=AO=5,
∴PH=PA+AH=9,
在Rt△POH中,OP==3.
【点评】本题考查了垂径定理:垂直于弦的直径平分这条弦,并且平分弦所对的两条弧.也考查了等腰三角形的判定和勾股定理.
37.如图,已知圆O的直径AB垂直于弦CD于点E,连接CO并延长交AD于点F,且CF⊥AD.
(1)请证明:E是OB的中点;
(2)若AB=6,求CD的长.
【分析】(1)要证E是OB的中点,只要证OE=OB=OC,即证出∠OCE=30°即可;
(2)在直角△OCE中,根据勾股定理就可以解得CE的长,进而求出CD的长.
【解答】(1)证明:连接AC,如图所示:
∵直径AB垂直于弦CD于点E,
∴,
∴AC=AD,
∵过圆心O的线CF⊥AD,
∴AF=DF,
即CF是AD的中垂线,
∴AC=CD,
∴AC=AD=CD.
即△ACD是等边三角形,
∴∠FCD=30°,
在Rt△COE中,OE=OC,
∴OE=OB,
∴点E为OB的中点;
(2)解:在Rt△OCE中,AB=6,
∴OC=AB=3,
又∵BE=OE,
∴OE=,
∴CE===,
∴CD=2CE=3.
【点评】本题考查垂径定理、等边三角形的判定、线段垂直平分线的性质、勾股定理等知识,解题的关键是灵活运用所学知识解决问题,属于中考常考题型.
38.如图,已知在⊙O中,直径MN=10,正方形ABCD的四个顶点分别在⊙O及半径OM、OP上,并且∠POM=45°,求正方形的边长.
【分析】证出△DCO是等腰直角三角形,得出DC=CO,求出BO=2AB,连接AO,得出AO=5,再根据勾股定理求出AB的长即可.
【解答】解:∵四边形ABCD是正方形,
∴∠ABC=∠BCD=90°,AB=BC=CD,
∴∠DCO=90°,
∵∠POM=45°,
∴∠CDO=45°,
∴CD=CO,
∴BO=BC+CO=BC+CD,
∴BO=2AB,
连接AO,如图:
∵MN=10,
∴AO=5,
在Rt△ABO中,AB2+BO2=AO2,
即AB2+(2AB)2=52,
解得:AB=,
则正方形ABCD的边长为.
【点评】此题考查了正方形的性质和等腰直角三角形的性质,解题的关键是证出△DCO是等腰直角三角形,得出BO=2AB,作出辅助线,利用勾股定理求解.
39.已知,如图,AB是⊙O的直径,M,N分别为AO、BO的中点,CM⊥AB,DN⊥AB,垂足分别为M,N.
求证:AC=BD.
【分析】连接OC、OD,根据已知条件,易证△OCM≌△ODN,根据全等三角形的性质可知,∠AOC=∠BOD,根据圆心角、弦、弧之间的关系定理可知,AC=BD.
【解答】证明:连接OC、OD,
∵AB是⊙O的直径,
∴AO=BO,
∵M,N分别为AO、BO的中点,
∴OM=ON,
∵CM⊥AB,DN⊥AB,
∴∠CMO=∠DNO=90°,
∴△OCM与△ODN都是直角三角形,
又∵OC=OD,
∴△OCM≌△ODN(HL),
∴∠AOC=∠BOD,
∴AC=BD.
【点评】本题考查了圆心角、弦、弧之间的关系定理,此定理应用非常广泛,为证明线段相等和角的相等提供了依据.
40.已知:如图,AB是⊙O的弦,半径OC交弦AB于点P,且AB=10cm,PB=4cm,PC=2cm,求半径OC的长.
【分析】过点O作OD⊥AB于D,连接OA,由垂径定理得AD=BD=AB=5,则DP=1,设OA=OC=r,在Rt△AOD和Rt△OPD中,由勾股定理得r2﹣52=(r﹣2)2﹣12,解得r=7即可.
【解答】解:过点O作OD⊥AB于D,连接OA,如图所示:
则AD=BD=AB=5,
∴DP=BD﹣PB=5﹣4=1,
设OA=OC=r,
在Rt△AOD和Rt△OPD中,由勾股定理得:OD2=OA2﹣AD2=OP2﹣DP2,
即r2﹣52=(r﹣2)2﹣12,
解得:r=7,
即半径OC的长为7cm.
【点评】本题考查了垂径定理、勾股定理;熟练掌握垂径定理,由勾股定理得出方程是解题的关键.
一.选择题(共12小题)
1.往直径为52cm的圆柱形容器内装入一些水以后,截面如图所示,若水面宽AB=48cm,则水的最大深度为( )
A.8cm
B.10cm
C.16cm
D.20cm
2.如图,在半径为3的⊙O中,AB是直径,AC是弦,D是的中点,AC与BD交于点E.若E是BD的中点,则AC的长是( )
A.
B.3
C.3
D.4
3.如图,⊙O的直径CD=20,AB是⊙O的弦,AB⊥CD,垂足为M,OM:OC=3:5,则AB的长为( )
A.8
B.12
C.16
D.2
4.如图,一条公路的转弯处是一段圆弧(),点O是这段弧所在圆的圆心,AB=40m,点C是的中点,点D是AB的中点,且CD=10m,则这段弯路所在圆的半径为( )
A.25m
B.24m
C.30m
D.60m
第1题
第2题
第3题
第4题
第5题
第6题
5.如图所示A、B、C、D四点在⊙O上的位置,其中=180°,且=,=.若阿超在上取一点P,在上取一点Q,使得∠APQ=130°,则下列叙述何者正确?( )
A.Q点在上,且>
B.Q点在上,且<
C.Q点在上,且>
D.Q点在上,且<
6.如图,AC是⊙O的直径,弦BD⊥AO于E,连接BC,过点O作OF⊥BC于F,若BD=8cm,AE=2cm,则OF的长度是( )
A.3cm
B.cm
C.2.5cm
D.cm
7.如图,AB是⊙O的直径,弦CD交AB于点P,AP=2,BP=6,∠APC=30°,则CD的长为( )
A.
B.2
C.2
D.8
8.如图,⊙O的半径OA=6,以A为圆心,OA为半径的弧交⊙O于B、C点,则BC=( )
A.
B.
C.
D.
9.已知AB,CD是⊙O的两条平行弦,AB=8,CD=6,⊙O的半径为5,则弦AB与CD的距离为( )
A.1
B.7
C.4或3
D.7或1
10.点A、C为半径是3的圆周上两点,点B为的中点,以线段BA、BC为邻边作菱形ABCD,顶点D恰在该圆直径的三等分点上,则该菱形的边长为( )
A.或2
B.或2
C.或2
D.或2
11.如图,CD为⊙O的直径,弦AB⊥CD,垂足为M,若AB=12,OM:MD=5:8,则⊙O的周长为( )
A.26π
B.13π
C.
D.
第7题
第8题
第11题
第12题
第13题
12.如图,已知⊙O的半径OB为3,且CD⊥AB,∠D=15°.则OE的长为( )
A.
B.
C.
D.3
二.填空题(共12小题)
13.我国古代数学经典著作《九章算术》中记载了一个“圆材埋壁”的问题:“今有圆材埋在壁中,不知大小.以锯锯之,深一寸,锯道长一尺.问径几何?”意思是:今有一圆柱形木材,埋在墙壁中,不知其大小.用锯去锯这木材,锯口深ED=1寸,锯道长AB=1尺(1尺=10寸).问这根圆形木材的直径是
寸.
14.在半径为的⊙O中,弦AB垂直于弦CD,垂足为P,AB=CD=4,则S△ACP=
.
15.已知⊙O的直径为10cm,AB,CD是⊙O的两条弦,AB∥CD,AB=8cm,CD=6cm,则AB与CD之间的距离为
cm.
16.如图,AB为⊙O的直径,弦CD⊥AB于点H,若AB=10,CD=8,则OH的长度为
.
17.如图,AB是⊙O的直径,C、D为半圆的三等分点,CE⊥AB于点E,∠ACE的度数为
.
18.已知⊙O的半径为10cm,AB,CD是⊙O的两条弦,AB∥CD,AB=16cm,CD=12cm,则弦AB和CD之间的距离是
cm.
19.如图,AB是⊙O的直径,CD为弦,CD⊥AB于E,若CD=6,BE=1,则⊙O的直径为
.
第16题
第17题
第19题
第20题
第21题
第22题
20.如图,在正方形纸片ABCD中,EF∥AD,M,N是线段EF的六等分点,若把该正方形纸片卷成一个圆柱,使点A与点D重合,此时,底面圆的直径为10cm,则圆柱上M,N两点间的距离是
cm.
21.如图,把一只篮球放在高为16cm的长方体纸盒中,发现篮球的一部分露出盒,其截面如图所示.若量得EF=24cm,则该篮球的半径为
cm.
22.如图平面直角坐标系中,⊙O的半径5?,弦AB的长为4,过点O做OC⊥AB于点C,⊙O内一点D的坐标为(﹣4,3),当弦AB绕点O顺时针旋转时,点D到AB的距离的最小值是
.
23.如图表示一圆柱形输水管的横截面,阴影部分为有水部分,如果水的最大深度
CD为2m,水面宽AB为8m,则输水管的半径为
m.
24.如图,在直角三角形ABC中,∠ACB=90°,AC=1,BC=2,以点C为圆心,
CA为半径的圆与AB交于点D,则AD的长为
.
三.解答题(共16小题)
25.如图所示,某地欲搭建一座圆弧型拱桥,跨度AB=32米,拱高CD=8米(C为AB的中点,D为弧AB的中点).
(1)求该圆弧所在圆的半径;
(2)在距离桥的一端4米处欲立一桥墩EF支撑,求桥墩的高度.
26.如图,在⊙O中,半径OC过弦AB的中点E,OC=2,OE=.
(1)求弦AB的长;
(2)求∠CAB的度数.
27.如图,已知MN是⊙O的直径,AB是⊙O的弦,AB⊥MN,点C在线段AB上,OC=AC=2,BC=4,求⊙O的半径.
28.如图,AB是⊙O的直径,弦CD⊥AB于E,连接AD,过点O作OF⊥AD于F,若CD=6,BE=1,求△AOF的面积.
29.如图,OA、OB、OC是⊙O的三条半径,弧AC等于弧BC,D、E分别是OA、OB的中点,CD与CE相等吗?为什么?
30.如图,两个同心圆的圆心为O,大圆的弦AB交小圆于C、D,求证:AC=BD.
31.如图,在⊙O中,弦BC与半径OA垂直于点D,连接AB、AC.点E为AC的中点,连接DE.
(1)若AB=6,求DE的长;
(2)若∠BAC=100°,求∠CDE的度数.
32.如图,已知圆O的直径AB垂直于弦CD于点E,连接CO并延长交AD于点F,且CF⊥AD.
(1)证明:点E是OB的中点;
(2)若AE=8,求CD的长.
33.如图,MB,MD是⊙O的两条弦,点A,C分别在弧MB,弧MD上,且AB=CD,点M是弧AC的中点.
(1)求证:MB=MD;
(2)过O作OE⊥MB于E,OE=1,⊙O的半径是2,求MD的长.
34.《九章算术》是我国古代著名数学经典,其中对勾股定理的论述比西方早一千多年,其中有这样一个问题:“今有圆材埋在壁中,不知大小:以锯锯之,深一寸,锯道长一尺.问径几何?”其意为:今有一圆柱形木材,埋在墙壁中,不知其大小,用锯去锯该材料,锯口深1寸,锯道长1尺.如图,已知弦AB=1尺,弓形高CD=1寸,(注:1尺=10寸)问这块圆柱形木材的直径是多少寸?
35.如图,某石拱桥的桥拱是圆弧形,拱的跨度AB为24m,点O是所在圆的圆心,⊙O的半径为13m,求桥拱的高度.(弧的中点到弦的距离)
36.如图,射线PG平分∠EPF,O为射线PG上一点,以O为圆心,5为半径作⊙O分别与∠EPF的两边相交于A、B和C、D,连接OA,且OA∥PE.
(1)求证:AP=AO;
(2)若弦AB=8,求OP的长.
37.如图,已知圆O的直径AB垂直于弦CD于点E,连接CO并延长交AD于点F,且CF⊥AD.
(1)请证明:E是OB的中点;
(2)若AB=6,求CD的长.
38.如图,已知在⊙O中,直径MN=10,正方形ABCD的四个顶点分别在⊙O及半径OM、OP上,并且∠POM=45°,求正方形的边长.
39.已知,如图,AB是⊙O的直径,M,N分别为AO、BO的中点,CM⊥AB,DN⊥AB,垂足分别为M,N.
求证:AC=BD.
40.已知:如图,AB是⊙O的弦,半径OC交弦AB于点P,且AB=10cm,PB=4cm,PC=2cm,求半径OC的长.
2.2圆的对称性(夯实基础)
参考答案与试题解析
一.选择题(共12小题)
1.往直径为52cm的圆柱形容器内装入一些水以后,截面如图所示,若水面宽AB=48cm,则水的最大深度为( )
A.8cm
B.10cm
C.16cm
D.20cm
【分析】连接OB,过点O作OC⊥AB于点D,交⊙O于点C,先由垂径定理求出BD的长,再根据勾股定理求出OD的长,进而可得出CD的长.
【解答】解:连接OB,过点O作OC⊥AB于点D,交⊙O于点C,如图所示:
∵AB=48cm,
∴BD=AB=×48=24(cm),
∵⊙O的直径为52cm,
∴OB=OC=26cm,
在Rt△OBD中,OD===10(cm),
∴CD=OC﹣OD=26﹣10=16(cm),
故选:C.
【点评】本题考查了垂径定理、勾股定理等知识;根据题意作出辅助线,构造出直角三角形是解答此题的关键.
2.如图,在半径为3的⊙O中,AB是直径,AC是弦,D是的中点,AC与BD交于点E.若E是BD的中点,则AC的长是( )
A.
B.3
C.3
D.4
【分析】连接OD,交AC于F,根据垂径定理得出OD⊥AC,AF=CF,进而证得DF=BC,根据三角形中位线定理求得OF=BC=DF,从而求得BC=DF=2,利用勾股定理即可求得AC.
【解答】解:连接OD,交AC于F,
∵D是的中点,
∴OD⊥AC,AF=CF,
∴∠DFE=90°,
∵OA=OB,AF=CF,
∴OF=BC,
∵AB是直径,
∴∠ACB=90°,
在△EFD和△ECB中
∴△EFD≌△ECB(AAS),
∴DF=BC,
∴OF=DF,
∵OD=3,
∴OF=1,
∴BC=2,
在Rt△ABC中,AC2=AB2﹣BC2,
∴AC===4,
故选:D.
【点评】本题考查了垂径定理,三角形全等的判定和性质,三角形中位线定理,熟练掌握性质定理是解题的关键.
3.如图,⊙O的直径CD=20,AB是⊙O的弦,AB⊥CD,垂足为M,OM:OC=3:5,则AB的长为( )
A.8
B.12
C.16
D.2
【分析】连接OA,先根据⊙O的直径CD=20,OM:OC=3:5求出OD及OM的长,再根据勾股定理可求出AM的长,进而得出结论.
【解答】解:连接OA,
∵⊙O的直径CD=20,OM:OC=3:5,
∴OC=10,OM=6,
∵AB⊥CD,
∴AM===8,
∴AB=2AM=16.
故选:C.
【点评】本题考查的是垂径定理,根据题意作出辅助线,构造出直角三角形是解答此题的关键.
4.如图,一条公路的转弯处是一段圆弧(),点O是这段弧所在圆的圆心,AB=40m,点C是的中点,点D是AB的中点,且CD=10m,则这段弯路所在圆的半径为( )
A.25m
B.24m
C.30m
D.60m
【分析】根据题意,可以推出AD=BD=20,若设半径为r,则OD=r﹣10,OB=r,结合勾股定理可推出半径r的值.
【解答】解:∵OC⊥AB,
∴AD=DB=20m,
在Rt△AOD中,OA2=OD2+AD2,
设半径为r得:r2=(r﹣10)2+202,
解得:r=25m,
∴这段弯路的半径为25m
故选:A.
【点评】本题主要考查垂径定理的应用、勾股定理的应用,关键在于设出半径为r后,用r表示出OD、OB的长度.
5.如图所示A、B、C、D四点在⊙O上的位置,其中=180°,且=,=.若阿超在上取一点P,在上取一点Q,使得∠APQ=130°,则下列叙述何者正确?( )
A.Q点在上,且>
B.Q点在上,且<
C.Q点在上,且>
D.Q点在上,且<
【分析】连接AD,OB,OC,根据题意得到∠BOC=∠DOC=45°,在圆周上取一点E连接AE,CE,由圆周角定理得到∠E=AOC=67.5°,求得∠ABC=112.5°<130°,取的中点F,连接OF,得到∠ABF=123.25°<130°,于是得到结论.
【解答】解:连接AD,OB,OC,
∵=180°,且=,=,
∴∠BOC=∠DOC=45°,
在圆周上取一点E连接AE,CE,
∴∠E=AOC=67.5°,
∴∠ABC=112.5°<130°,
取的中点F,连接OF,
则∠AOF=∠AOB+∠BOF=90°+22.5°=112.5°,
∴∠ABF=∠ABO+∠OBF=45°+(180°﹣22.5°)=123.75°<130°,
∴Q点在上,且<,
故选:B.
【点评】本题考查了圆心角,弧,弦的关系,圆内接四边形的性质,圆周角定理,正确的理解题意是解题的关键.
6.如图,AC是⊙O的直径,弦BD⊥AO于E,连接BC,过点O作OF⊥BC于F,若BD=8cm,AE=2cm,则OF的长度是( )
A.3cm
B.cm
C.2.5cm
D.cm
【分析】根据垂径定理得出AB的长,进而利用中位线定理得出OF即可.
【解答】解:连接AB,OB,
∵AC是⊙O的直径,弦BD⊥AO于E,BD=8cm,AE=2cm,
在Rt△ABE中,AE2+BE2=AB2,
即AB=,
∵OA=OC,OB=OC,OF⊥BC,
∴BF=FC,
∴OF=.
故选:D.
【点评】此题考查垂径定理,关键是根据垂径定理得出OE的长.
7.如图,AB是⊙O的直径,弦CD交AB于点P,AP=2,BP=6,∠APC=30°,则CD的长为( )
A.
B.2
C.2
D.8
【分析】作OH⊥CD于H,连接OC,如图,根据垂径定理由OH⊥CD得到HC=HD,再利用AP=2,BP=6可计算出半径OA=4,则OP=OA﹣AP=2,接着在Rt△OPH中根据含30度的直角三角形的性质计算出OH=OP=1,然后在Rt△OHC中利用勾股定理计算出CH=,所以CD=2CH=2.
【解答】解:作OH⊥CD于H,连接OC,如图,
∵OH⊥CD,
∴HC=HD,
∵AP=2,BP=6,
∴AB=8,
∴OA=4,
∴OP=OA﹣AP=2,
在Rt△OPH中,∵∠OPH=30°,
∴∠POH=60°,
∴OH=OP=1,
在Rt△OHC中,∵OC=4,OH=1,
∴CH==,
∴CD=2CH=2.
故选:C.
【点评】本题考查了垂径定理:垂直于弦的直径平分这条弦,并且平分弦所对的两条弧.也考查了勾股定理以及含30度的直角三角形的性质.
8.如图,⊙O的半径OA=6,以A为圆心,OA为半径的弧交⊙O于B、C点,则BC=( )
A.
B.
C.
D.
【分析】根据垂径定理先求BC一半的长,再求BC的长.
【解答】解:设OA与BC相交于D点.
∵AB=OA=OB=6
∴△OAB是等边三角形.
又根据垂径定理可得,OA平分BC,
利用勾股定理可得BD==3
所以BC=6.
故选:A.
【点评】本题的关键是利用垂径定理和勾股定理.
9.已知AB,CD是⊙O的两条平行弦,AB=8,CD=6,⊙O的半径为5,则弦AB与CD的距离为( )
A.1
B.7
C.4或3
D.7或1
【分析】连接OC、OA,作直线OF⊥AB于E,交CD于F,则EF⊥CD,根据垂径定理求出CF,AE,根据勾股定理求出OE、OF,即可得出答案.
【解答】解:如图所示,连接OA,OC.作直线OF⊥AB于E,交CD于F,则EF⊥CD,
∵OE⊥AB,OF⊥CD,
∴AE=AB=4,CF=CD=3,
根据勾股定理,得
OE==3,OF==4,
所以当AB和CD在圆心的同侧时,则EF=OF﹣OE=1,
当AB和CD在圆心的异侧时,则EF=OF+OE=7.
故选:D.
【点评】本题考查了垂径定理的知识,此题综合运用了垂径定理和勾股定理,特别注意有时要考虑两种情况.
10.点A、C为半径是3的圆周上两点,点B为的中点,以线段BA、BC为邻边作菱形ABCD,顶点D恰在该圆直径的三等分点上,则该菱形的边长为( )
A.或2
B.或2
C.或2
D.或2
【分析】过B作直径,连接AC交BO于E,如图①,根据已知条件得到BD=×2×3=2,如图②,BD=×2×3=4,求得OD=1,OE=2,DE=1,连接OD,根据勾股定理得到结论,
【解答】解:过B作直径,连接AC交BO于E,
∵点B为的中点,
∴BD⊥AC,
如图①,
∵点D恰在该圆直径的三等分点上,
∴BD=×2×3=2,
∴OD=OB﹣BD=1,
∵四边形ABCD是菱形,
∴DE=BD=1,
∴OE=2,
连接OC,
∵CE==,
∴边CD==;
如图②,BD=×2×3=4,
同理可得,OD=1,OE=1,DE=2,
连接OC,
∵CE===2,
∴边CD===2,
故选:D.
【点评】本题考查了圆心角,弧,弦的关系,勾股定理,菱形的性质,正确的作出图形是解题的关键.
11.如图,CD为⊙O的直径,弦AB⊥CD,垂足为M,若AB=12,OM:MD=5:8,则⊙O的周长为( )
A.26π
B.13π
C.
D.
【分析】连接OA,根据垂径定理得到AM=AB=6,设OM=5x,DM=8x,得到OA=OD=13x,根据勾股定理得到OA=×13,于是得到结论.
【解答】解:连接OA,
∵CD为⊙O的直径,弦AB⊥CD,
∴AM=AB=6,
∵OM:MD=5:8,
∴设OM=5x,DM=8x,
∴OA=OD=13x,
∴AM=12x=6,
∴x=,
∴OA=×13,
∴⊙O的周长=2OA?π=13π,
故选:B.
【点评】本题考查的是垂径定理,根据题意作出辅助线,构造出直角三角形,利用勾股定理求解是解答此题的关键.
12.如图,已知⊙O的半径OB为3,且CD⊥AB,∠D=15°.则OE的长为( )
A.
B.
C.
D.3
【分析】连接OA,先根据圆O的直径为6求出OA的长,再由CD⊥AB得出∠AEO=90°,由圆周角定理求出∠AOE的度数,根据直角三角形的性质即可得出结论.
【解答】解:连接OA,
∵圆O的直径为6,
∴OA=3.
∵CD⊥AB,
∴∠AEO=90°.
∵∠D=15°,
∴∠AOE=30°,
∴OE=OA?cos30°=3×=.
故选:A.
【点评】本题考查的是垂径定理,熟知平分弦的直径平分这条弦,并且平分弦所对的两条弧是解答此题的关键.
二.填空题(共12小题)
13.我国古代数学经典著作《九章算术》中记载了一个“圆材埋壁”的问题:“今有圆材埋在壁中,不知大小.以锯锯之,深一寸,锯道长一尺.问径几何?”意思是:今有一圆柱形木材,埋在墙壁中,不知其大小.用锯去锯这木材,锯口深ED=1寸,锯道长AB=1尺(1尺=10寸).问这根圆形木材的直径是 26 寸.
【分析】根据题意可得OE⊥AB,由垂径定理可得尺=5寸,设半径OA=OE=r寸,则OD=r﹣1,在Rt△OAD中,根据勾股定理可得:(r﹣1)2+52=r2,解方程可得出木材半径,即可得出木材直径.
【解答】解:由题意可知OE⊥AB,
∵OE为⊙O半径,
∴尺=5寸,
设半径OA=OE=r寸,
∵ED=1,
∴OD=r﹣1,
则Rt△OAD中,根据勾股定理可得:(r﹣1)2+52=r2,
解得:r=13,
∴木材直径为26寸;
故答案为:26.
【点评】本题考查垂径定理结合勾股定理计算半径长度.如果题干中出现弦的垂线或者弦的中点,则可验证是否满足垂径定理;与圆有关的题目中如果求弦长或者求半径直径,也可以从题中寻找是否有垂径定理,然后构造直角三角形,用勾股定理求解.
14.在半径为的⊙O中,弦AB垂直于弦CD,垂足为P,AB=CD=4,则S△ACP= 或或 .
【分析】如图1,作OE⊥AB于E,OF⊥CD于F,连接OD、OB,如图,根据垂径定理得到AE=BE=AB=2,DF=CF=CD=2,根据勾股定理在Rt△OBE中计算出OE=1,同理可得OF=1,接着证明四边形OEPF为正方形,于是得到PA=PC=1,根据三角形面积公式求得即可.
【解答】解:作OE⊥AB于E,OF⊥CD于F,连接OD、OB,
则AE=BE=AB=2,DF=CF=CD=2,
如图1,
在Rt△OBE中,∵OB=,BE=2,
∴OE==1,
同理可得OF=1,
∵AB⊥CD,
∴四边形OEPF为矩形,
∴PE=PF=1,
∴PA=PC=1,
∴S△APC==;
如图2,
同理:S△APC==;
如图3,
同理:S△APC==;
故答案为:或或.
【点评】本题考查了垂径定理:垂直于弦的直径平分这条弦,并且平分弦所对的两条弧.也考查了勾股定理.
15.已知⊙O的直径为10cm,AB,CD是⊙O的两条弦,AB∥CD,AB=8cm,CD=6cm,则AB与CD之间的距离为 1或7 cm.
【分析】作OE⊥AB于E,延长EO交CD于F,连接OA、OC,如图,利用平行线的性质OF⊥CD,根据垂径定理得到AE=BE=4,CF=DF=3,则利用勾股定理可计算出OE=3,OF=4,讨论:当点O在AB与CD之间时,EF=OF+OE;当点O不在AB与CD之间时,EF=OF﹣OE.
【解答】解:作OE⊥AB于E,延长EO交CD于F,连接OA、OC,如图,
∵AB∥CD,OE⊥AB,
∴OF⊥CD,
∴AE=BE=AB=4cm,CF=DF=CD=3cm,
在Rt△OAE中,OE===3cm,
在Rt△OCF中,OF===4cm,
当点O在AB与CD之间时,如图1,EF=OF+OE=4+3=7cm;
当点O不在AB与CD之间时,如图2,EF=OF﹣OE=4﹣3=1cm;
综上所述,AB与CD之间的距离为1cm或7cm.
故答案为1或7.
【点评】本题考查了垂径定理:垂直于弦的直径平分这条弦,并且平分弦所对的两条弧.注意分类讨论.
16.如图,AB为⊙O的直径,弦CD⊥AB于点H,若AB=10,CD=8,则OH的长度为 3 .
【分析】根据垂径定理由CD⊥AB得到CH=CD=4,再根据勾股定理计算出OH=3.
【解答】解:连接OC,
∵CD⊥AB,
∴CH=DH=CD=×8=4,
∵直径AB=10,
∴OC=5,
在Rt△OCH中,OH==3,
故答案为:3.
【点评】本题考查了垂径定理:垂直于弦的直径平分这条弦,并且平分弦所对的两条弧.
17.如图,AB是⊙O的直径,C、D为半圆的三等分点,CE⊥AB于点E,∠ACE的度数为 30° .
【分析】想办法证明△AOC是等边三角形即可解决问题.
【解答】解:如图,连接OC.
∵AB是直径,==,
∴∠AOC=∠COD=∠DOB=60°,
∵OA=OC,
∴△AOC是等边三角形,
∴∠A=60°,
∵CE⊥OA,
∴∠AEC=90°,
∴∠ACE=90°﹣60°=30°.
故答案为30°
【点评】本题考查等弧所对的圆心角相等的性质、等边三角形的判定和性质等知识,解题的关键是熟练掌握基本知识,属于中考常考题型.
18.已知⊙O的半径为10cm,AB,CD是⊙O的两条弦,AB∥CD,AB=16cm,CD=12cm,则弦AB和CD之间的距离是 2或14 cm.
【分析】分两种情况进行讨论:①弦AB和CD在圆心同侧;②弦AB和CD在圆心异侧;作出半径和弦心距,利用勾股定理和垂径定理求解即可,小心别漏解.
【解答】解:①当弦AB和CD在圆心同侧时,如图,
∵AB=16cm,CD=12cm,
∴AE=8cm,CF=6cm,
∵OA=OC=10cm,
∴EO=6cm,OF=8cm,
∴EF=OF﹣OE=2cm;
②当弦AB和CD在圆心异侧时,如图,
∵AB=16cm,CD=12cm,
∴AF=8cm,CE=6cm,
∵OA=OC=10cm,
∴OF=6cm,OE=8cm,
∴EF=OF+OE=14cm.
∴AB与CD之间的距离为14cm或2cm.
故答案为:2或14.
【点评】本题考查了勾股定理和垂径定理的应用.此题难度适中,解题的关键是注意掌握数形结合思想与分类讨论思想的应用,小心别漏解.
19.
如图,AB是⊙O的直径,CD为弦,CD⊥AB于E,若CD=6,BE=1,则⊙O的直径为 10 .
【分析】首先连接OD,并设OD=x,然后在△ODE中,由勾股定理,求出OD的长,即可求出⊙O的直径为多少.
【解答】解:如图,连接OD,设OD=x,,
∵AB是⊙O的直径,而且CD⊥AB于E,
∴DE=CE=6÷2=3,
在Rt△ODE中,
x2=(x﹣1)2+32,
解得x=5,
∵5×2=10,
∴⊙O的直径为10.
故答案为:10.
【点评】此题主要考查了垂径定理以及勾股定理的应用,要熟练掌握,解答此题的关键是求出OD的长度是多少.
20.如图,在正方形纸片ABCD中,EF∥AD,M,N是线段EF的六等分点,若把该正方形纸片卷成一个圆柱,使点A与点D重合,此时,底面圆的直径为10cm,则圆柱上M,N两点间的距离是 5 cm.
【分析】根据题意得到MN=BC,当正方形纸片卷成一个圆柱时,EF卷成一个圆,线段卷成圆上一段弧,该段弧所对的圆心角为×360°,要求圆柱上M,N两点间的距离即求弦MN的长.
【解答】解:根据题意得:EF=AD=BC,MN=2EM=EF,
把该正方形纸片卷成一个圆柱,使点A与点D重合,则线段EF形成一直径为10cm的圆,线段EF为圆上的一段弧.
所对的圆心角为:×360°=120°,
所以圆柱上M,N两点间的距离为:2×5×sin60°=5cm.
故答案为:5.
【点评】此题实质考查了圆上弦的计算,需要先找出圆心角再根据弦长公式计算,熟练掌握公式及性质是解本题的关键.
21.如图,把一只篮球放在高为16cm的长方体纸盒中,发现篮球的一部分露出盒,其截面如图所示.若量得EF=24cm,则该篮球的半径为 12.5 cm.
【分析】取EF的中点M,作MN⊥AD于点M,取MN上的球心O,连接OF,设OF=x,则OM=16﹣x,MF=12,在Rt△MOF中利用勾股定理求得OF的长即可.
【解答】解:EF的中点M,作MN⊥AD于点M,取MN上的球心O,连接OF,
∵四边形ABCD是矩形,
∴∠C=∠D=90°,
∴四边形CDMN是矩形,
∴MN=CD=16cm,
设OF=xcm,则ON=OF,
∴OM=MN﹣ON=16﹣x,MF=12cm,
在直角三角形OMF中,OM2+MF2=OF2
即:(16﹣x)2+122=x2
解得:x=12.5(cm),
故答案为:12.5.
【点评】本题主考查垂径定理、矩形的性质及勾股定理的应用,正确作出辅助线构造直角三角形是解题的关键.
22.如图平面直角坐标系中,⊙O的半径5?,弦AB的长为4,过点O做OC⊥AB于点C,⊙O内一点D的坐标为(﹣4,3),当弦AB绕点O顺时针旋转时,点D到AB的距离的最小值是 6 .
【分析】连接OB,如图,利用垂径定理得到AC=BC=2,则利用勾股定理可计算出OC=11,利用垂线段最短,当OC经过点D时,点D到AB的距离的最小,然后计算出OD的长,从而得到点D到AB的距离的最小值.
【解答】解:连接OB,如图,
∵OC⊥AB,
∴AC=BC=AB=2,
在Rt△OBC中,OC===11,
当OC经过点D时,点D到AB的距离的最小,
∵OD==5,
∴点D到AB的距离的最小值为11﹣5=6.
故答案为6.
【点评】本题考查了垂径定理:垂直于弦的直径平分这条弦,并且平分弦所对的两条弧.也考查了勾股定理.
23.如图表示一圆柱形输水管的横截面,阴影部分为有水部分,如果水的最大深度CD为2m,水面宽AB为8m,则输水管的半径为 5 m.
【分析】由垂径定理可知AC=4m,设OA=rm,则OC=(r﹣1)m,在Rt△AOC中,再利用勾股定理即可求出r的值.
【解答】解:由题意得:OD⊥AB,
∴AC=AB=×8=4(m),
设OA=rm,则OC=OD﹣CD=(r﹣2)m,
在Rt△AOC中,由勾股定理得:OA2=OC2+AC2,
即r2=(r﹣2)2+42,
解得:r=5,
即输水管的半径为5m,
故答案为:5.
【点评】本题考查的是垂径定理的应用及勾股定理,熟练掌握垂径定理,由勾股定理得出方程是解题的关键.
24.如图,在直角三角形ABC中,∠ACB=90°,AC=1,BC=2,以点C为圆心,CA为半径的圆与AB交于点D,则AD的长为 .
【分析】作CE⊥AB于E,根据勾股定理得到AB=,利用三角形面积公式求出CE,根据勾股定理求出AE,根据垂径定理计算即可.
【解答】解:作CE⊥AB于E,
则AE=AD,
∵∠ACB=90°,AC=1,BC=2,
∴AB==,
×AB×CE=AC×BC,即×CE=,
解得,CE=,
AE==,
则AD=2AE=,
故答案为:.
【点评】本题考查的是勾股定理和垂径定理的应用,垂径定理:垂直弦的直径平分这条弦,并且平分弦所对的两条弧.
三.解答题(共16小题)
25.如图所示,某地欲搭建一座圆弧型拱桥,跨度AB=32米,拱高CD=8米(C为AB的中点,D为弧AB的中点).
(1)求该圆弧所在圆的半径;
(2)在距离桥的一端4米处欲立一桥墩EF支撑,求桥墩的高度.
【分析】(1)设弧AB所在的圆心为O,C为弧AB的中点,CD⊥AB于D,延长CD经过O点,设⊙O的半径为R,利用勾股定理求出即可;
(2)利用垂径定理以及勾股定理得出AO的长,再求出EF的长即可.
【解答】解:(1)设弧AB所在的圆心为O,C为弧AB的中点,CD⊥AB于D,延长CD经过O点,设⊙O的半径为R,
在Rt△OBD中,OB2=OD2+DB2,
∴R2=(R﹣8)2+162,
解得R=20;
(2)在圆弧型中设点F′在弧AB上,作F′E′⊥AB于E′,
OH⊥F′E′于H,则OH=DE′=16﹣4=12,OF′=R=20,
在Rt△OHF′中,HF′=,
∵HE′=OD=OC﹣CD=20﹣8=12,E′F′=HF′﹣HE′=16﹣12=4(米),
∴在离桥的一端4米处,圆弧型桥墩高4米.
【点评】此题主要考查了垂径定理的应用,根据题意画出图形结合勾股定理得出是解题关键.
26.如图,在⊙O中,半径OC过弦AB的中点E,OC=2,OE=.
(1)求弦AB的长;
(2)求∠CAB的度数.
【分析】(1)连接OB,先由垂径定理得OC⊥AB,AE=BE,OB=OC=2,再由勾股定理求出BE=,即可求解;
(2)先证△BOE是等腰直角三角形,得∠BOC=45°,再由圆周角定理即可求解.
【解答】解:(1)连接OB,如图所示:
∵半径OC过弦AB的中点E,
∴OC⊥AB,AE=BE,OB=OC=2,
∴BE===,
∴AB=2BE=2;
(2)由(1)得:BE=OE,OC⊥AB,
∴△BOE是等腰直角三角形,
∴∠BOC=45°,
∴∠CAB=∠BOC=22.5°.
【点评】本题考查了垂径定理、勾股定理、等腰直角三角形的判定与性质以及圆周角定理等知识;熟练掌握垂径定理和勾股定理是解题的关键.
27.如图,已知MN是⊙O的直径,AB是⊙O的弦,AB⊥MN,点C在线段AB上,OC=AC=2,BC=4,求⊙O的半径.
【分析】连接OB,先由垂径定理得AD=BD=AB=3,则CD=AD﹣AC=1,再由勾股定理求出OD=,然后由勾股定理求出OB即可.
【解答】解:连接OB,设AB与MN交于点D,如图所示:
∵AC=2,BC=4,
∴AB=AC+BC=6,
∵AB⊥MN,
∴AD=BD=AB=3,∠ODC=∠ODB=90°,
∴CD=AD﹣AC=1,
∴OD===,
∴OB===2,
即⊙O的半径为2.
【点评】本题考查了垂径定理和勾股定理;熟练掌握垂径定理和勾股定理是解题的关键.
28.如图,AB是⊙O的直径,弦CD⊥AB于E,连接AD,过点O作OF⊥AD于F,若CD=6,BE=1,求△AOF的面积.
【分析】连接OD,先由垂径定理得CE=DE=CD=3,设⊙O的半径为r,则OE=r﹣1,OD=r,由勾股定理求出r=5,则OE=4,AE=9,求出S△AED=,S△OED=6,则S△AOD=S△AED﹣S△OED=,即可解决问题.
【解答】解:连接OD,如图所示:
∵CD⊥AB,
∴CE=DE=CD=3,
设⊙O的半径为r,
则OE=r﹣1,OD=r,
在Rt△ODE中,由勾股定理得:(r﹣1)2+32=r2,
解得:r=5,
∴OE=4,AE=5+4=9,
∴S△AED=AE?DE=×9×3=,S△OED=OE?DE=×4×3=6,
∴S△AOD=S△AED﹣S△OED=﹣6=,
∵OF⊥AD,OA=OD,
∴AF=DF,
∴S△AOF=S△AOD=×=.
【点评】本题考查了垂径定理、等腰三角形的性质、勾股定理、三角形面积的计算等知识;熟练掌握垂径定理和勾股定理是解题的关键.
29.如图,OA、OB、OC是⊙O的三条半径,弧AC等于弧BC,D、E分别是OA、OB的中点,CD与CE相等吗?为什么?
【分析】根据弧与圆心角的关系,可得∠AOC=∠BOC,又由D、E分别是半径OA、OB的中点,可得OD=OE,利用SAS判定△DOC≌△EOC,继而证得结论.
【解答】解:CD=CE,理由如下:
∵弧AC和弧BC相等,
∴∠AOC=∠BOC,
又∵OA=OB,D、E分别是OA、OB的中点,
∴OD=OE,
在△DOC和△EOC中,
,
∴△DOC≌△EOC(SAS),
∴CD=CE.
【点评】此题考查了弧与圆心角的关系以及全等三角形的判定与性质;证明三角形全等是解决问题的关键.
30.如图,两个同心圆的圆心为O,大圆的弦AB交小圆于C、D,求证:AC=BD.
【分析】过O作OE⊥AB于E,由垂径定理得出AE=BE,CE=DE,相减即可得出答案.
【解答】证明:
过O作OE⊥AB于E,
则OE⊥CD,
∵OE过O,
∴由垂径定理得:AE=BE,CE=DE,
∴AE﹣CE=BE﹣DE,
即AC=BD.
【点评】本题考查了垂径定理的应用,关键是作辅助线后得出AE=BE,CE=DE.
31.如图,在⊙O中,弦BC与半径OA垂直于点D,连接AB、AC.点E为AC的中点,连接DE.
(1)若AB=6,求DE的长;
(2)若∠BAC=100°,求∠CDE的度数.
【分析】(1)根据垂径定理得到=,则AC=AB=6,然后根据直角三角形斜边上的中线性质得到DE的长;
(2)利用等腰三角形的性质和三角形的内角和计算出∠C=40°,然后利用ED=EC得到∠CDE=∠C=40°.
【解答】解:(1)∵BC⊥OA,
∴=,∠ADC=90°,
∴AC=AB=6,
∵点E为AC的中点,
∴DE=AC=3;
(2)∵AB=AC,
∴∠B=∠C,
∵∠BAC=100°,
∴∠C=(180°﹣100°)=40°,
∵点E为AC的中点,
∴ED=EC,
∴∠CDE=∠C=40°.
【点评】本题考查了垂径定理:直于弦的直径平分这条弦,并且平分弦所对的两条弧.也考查了直角三角形斜边上的中线性质.
32.如图,已知圆O的直径AB垂直于弦CD于点E,连接CO并延长交AD于点F,且CF⊥AD.
(1)证明:点E是OB的中点;
(2)若AE=8,求CD的长.
【分析】(1)要证E是OB的中点,只要证OE=OB=OC,即证出∠OCE=30°即可;
(2)在直角△ACE中,根据∠CAB=30°就可以解得CE的长,进而求出CD的长.
【解答】(1)证明:连接AC,如图,
∵直径AB垂直于弦CD于点E,
∴=,
∴AC=AD,
∵过圆心O的线段CF⊥AD,
∴AF=DF,即CF是AD的中垂线,
∴AC=CD,
∴AC=AD=CD.
即△ACD是等边三角形,
∴∠FCD=30°,
在Rt△COE中,OE=OC,
∴OE=OB,
∴点E为OB的中点;
(2)解:∵△ACD是等边三角形,AB⊥CD,
∴∠CAE=30°,
∴CE=AE×tan30°=8×=,
∵直径AB垂直于弦CD于点E,
∴CD=2CE=.
【点评】本题考查垂径定理、等边三角形的判定、线段垂直平分线的性质、解直角三角形等知识,解题的关键是掌握垂直于弦的直径平分这条弦,并且平分弦所对的两条弧.
33.如图,MB,MD是⊙O的两条弦,点A,C分别在弧MB,弧MD上,且AB=CD,点M是弧AC的中点.
(1)求证:MB=MD;
(2)过O作OE⊥MB于E,OE=1,⊙O的半径是2,求MD的长.
【分析】(1)根据圆心角、弦、弧、弦心距之间的关系得出=即可;
(2)根据垂径定理,勾股定理求出ME,进而求出MB即可.
【解答】证明:(1)∵AB=CD,
∴=,
又∵点M是弧AC的中点,
∴=,
∴+=+,
即:=,
∴MB=MD;
(2)过O作OE⊥MB于E,则ME=BE,连接OM,
在Rt△MOE中,OE=1,⊙O的半径OM=2,
∴ME===,
∴MD=MB=2ME=2.
【点评】本题考查圆心角、弦、弧之间的关系,垂径定理、勾股定理等知识,掌握垂径定理、勾股定理是正确计算的前提.
34.《九章算术》是我国古代著名数学经典,其中对勾股定理的论述比西方早一千多年,其中有这样一个问题:“今有圆材埋在壁中,不知大小:以锯锯之,深一寸,锯道长一尺.问径几何?”其意为:今有一圆柱形木材,埋在墙壁中,不知其大小,用锯去锯该材料,锯口深1寸,锯道长1尺.如图,已知弦AB=1尺,弓形高CD=1寸,(注:1尺=10寸)问这块圆柱形木材的直径是多少寸?
【分析】设⊙O的半径为r.在Rt△ADO中,AD=5,OD=r﹣1,OA=r,则有r2=52+(r﹣1)2,解方程即可.
【解答】解:设⊙O的半径为r.
∵OC⊥AB,
∴AD=BD=AB=5,
在Rt△ADO中,AD=5,OD=r﹣1,OA=r,
则有:r2=52+(r﹣1)2,
解得:r=13,
∴⊙O的直径为26寸.
【点评】本题考查了垂径定理、勾股定理等知识,解题的关键是学会利用参数构建方程解决问题,属于中考常考题型.
35.如图,某石拱桥的桥拱是圆弧形,拱的跨度AB为24m,点O是所在圆的圆心,⊙O的半径为13m,求桥拱的高度.(弧的中点到弦的距离)
【分析】由垂径定理得AD=BD=×24=12(m),设CD=xm,则OD=(13﹣x)m,在Rt△AOD中,根据勾股定理得出方程,解方程即可.
【解答】解:如图所示:过O作OD⊥AB交于C,垂足为D,
则AD=BD=×24=12(m),
设CD=xm,则OD=(13﹣x)m,
根据勾股定理得:122+(13﹣x)2=132,
解得:x=8,
即桥拱的高度为8m.
【点评】本题考查了垂径定理和勾股定理等知识;熟练掌握垂径定理,由勾股定理得出方程是解题的关键.
36.如图,射线PG平分∠EPF,O为射线PG上一点,以O为圆心,5为半径作⊙O分别与∠EPF的两边相交于A、B和C、D,连接OA,且OA∥PE.
(1)求证:AP=AO;
(2)若弦AB=8,求OP的长.
【分析】(1)∠APO=∠AOP得到AP=AO;
(2)过O点作OH⊥AB于H,如图,根据垂径定理得到AH=BH=4,则可利用勾股定理可计算出OH=3,然后在Rt△POH中利用勾股定理计算OP.
【解答】(1)证明:∵PG平分∠EPF,
∴∠DPO=∠APO,
∵OA∥PE,
∴∠DPO=∠AOP,
∴∠APO=∠AOP,
∴AP=AO;
(2)解:过O点作OH⊥AB于H,如图,则AH=BH=AB=4,
在Rt△AOH中,∵OA=5,AH=4,
∴OH==3,
∵AP=AO=5,
∴PH=PA+AH=9,
在Rt△POH中,OP==3.
【点评】本题考查了垂径定理:垂直于弦的直径平分这条弦,并且平分弦所对的两条弧.也考查了等腰三角形的判定和勾股定理.
37.如图,已知圆O的直径AB垂直于弦CD于点E,连接CO并延长交AD于点F,且CF⊥AD.
(1)请证明:E是OB的中点;
(2)若AB=6,求CD的长.
【分析】(1)要证E是OB的中点,只要证OE=OB=OC,即证出∠OCE=30°即可;
(2)在直角△OCE中,根据勾股定理就可以解得CE的长,进而求出CD的长.
【解答】(1)证明:连接AC,如图所示:
∵直径AB垂直于弦CD于点E,
∴,
∴AC=AD,
∵过圆心O的线CF⊥AD,
∴AF=DF,
即CF是AD的中垂线,
∴AC=CD,
∴AC=AD=CD.
即△ACD是等边三角形,
∴∠FCD=30°,
在Rt△COE中,OE=OC,
∴OE=OB,
∴点E为OB的中点;
(2)解:在Rt△OCE中,AB=6,
∴OC=AB=3,
又∵BE=OE,
∴OE=,
∴CE===,
∴CD=2CE=3.
【点评】本题考查垂径定理、等边三角形的判定、线段垂直平分线的性质、勾股定理等知识,解题的关键是灵活运用所学知识解决问题,属于中考常考题型.
38.如图,已知在⊙O中,直径MN=10,正方形ABCD的四个顶点分别在⊙O及半径OM、OP上,并且∠POM=45°,求正方形的边长.
【分析】证出△DCO是等腰直角三角形,得出DC=CO,求出BO=2AB,连接AO,得出AO=5,再根据勾股定理求出AB的长即可.
【解答】解:∵四边形ABCD是正方形,
∴∠ABC=∠BCD=90°,AB=BC=CD,
∴∠DCO=90°,
∵∠POM=45°,
∴∠CDO=45°,
∴CD=CO,
∴BO=BC+CO=BC+CD,
∴BO=2AB,
连接AO,如图:
∵MN=10,
∴AO=5,
在Rt△ABO中,AB2+BO2=AO2,
即AB2+(2AB)2=52,
解得:AB=,
则正方形ABCD的边长为.
【点评】此题考查了正方形的性质和等腰直角三角形的性质,解题的关键是证出△DCO是等腰直角三角形,得出BO=2AB,作出辅助线,利用勾股定理求解.
39.已知,如图,AB是⊙O的直径,M,N分别为AO、BO的中点,CM⊥AB,DN⊥AB,垂足分别为M,N.
求证:AC=BD.
【分析】连接OC、OD,根据已知条件,易证△OCM≌△ODN,根据全等三角形的性质可知,∠AOC=∠BOD,根据圆心角、弦、弧之间的关系定理可知,AC=BD.
【解答】证明:连接OC、OD,
∵AB是⊙O的直径,
∴AO=BO,
∵M,N分别为AO、BO的中点,
∴OM=ON,
∵CM⊥AB,DN⊥AB,
∴∠CMO=∠DNO=90°,
∴△OCM与△ODN都是直角三角形,
又∵OC=OD,
∴△OCM≌△ODN(HL),
∴∠AOC=∠BOD,
∴AC=BD.
【点评】本题考查了圆心角、弦、弧之间的关系定理,此定理应用非常广泛,为证明线段相等和角的相等提供了依据.
40.已知:如图,AB是⊙O的弦,半径OC交弦AB于点P,且AB=10cm,PB=4cm,PC=2cm,求半径OC的长.
【分析】过点O作OD⊥AB于D,连接OA,由垂径定理得AD=BD=AB=5,则DP=1,设OA=OC=r,在Rt△AOD和Rt△OPD中,由勾股定理得r2﹣52=(r﹣2)2﹣12,解得r=7即可.
【解答】解:过点O作OD⊥AB于D,连接OA,如图所示:
则AD=BD=AB=5,
∴DP=BD﹣PB=5﹣4=1,
设OA=OC=r,
在Rt△AOD和Rt△OPD中,由勾股定理得:OD2=OA2﹣AD2=OP2﹣DP2,
即r2﹣52=(r﹣2)2﹣12,
解得:r=7,
即半径OC的长为7cm.
【点评】本题考查了垂径定理、勾股定理;熟练掌握垂径定理,由勾股定理得出方程是解题的关键.
同课章节目录
- 第1章 一元二次方程
- 1.1 一元二次方程
- 1.2 一元二次方程的解法
- 1.3 一元二次方程的根与系数的关系
- 1.4 用一元二次方程解决问题
- 数学活动 矩形绿地中的花圃设计
- 第2章 对称图形——圆
- 2.1 圆
- 2.2 圆的对称性
- 2.3 确定圆的条件
- 2.4 圆周角
- 2.5 直线与圆的位置关系
- 2.6 正多边形与圆
- 2.7 弧长及扇形的面积
- 2.8 圆锥的侧面积
- 数学活动 图形的密铺
- 第3章 数据的集中趋势和离散程度
- 3.1 平均数
- 3.2 中位数与众数
- 3.3 用计算器求平均数
- 3.4 方差
- 3.5 用计算器求方差
- 数学活动 估测时间
- 第4章 等可能条件下的概率
- 4.1 等可能性
- 4.2 等可能条件下的概率(一)
- 4.3 等可能条件下的概率(二)
- 数学活动 调查“小概率事件”
