3.1密度的计算同步练习(含答案)
文档属性
| 名称 | 3.1密度的计算同步练习(含答案) | 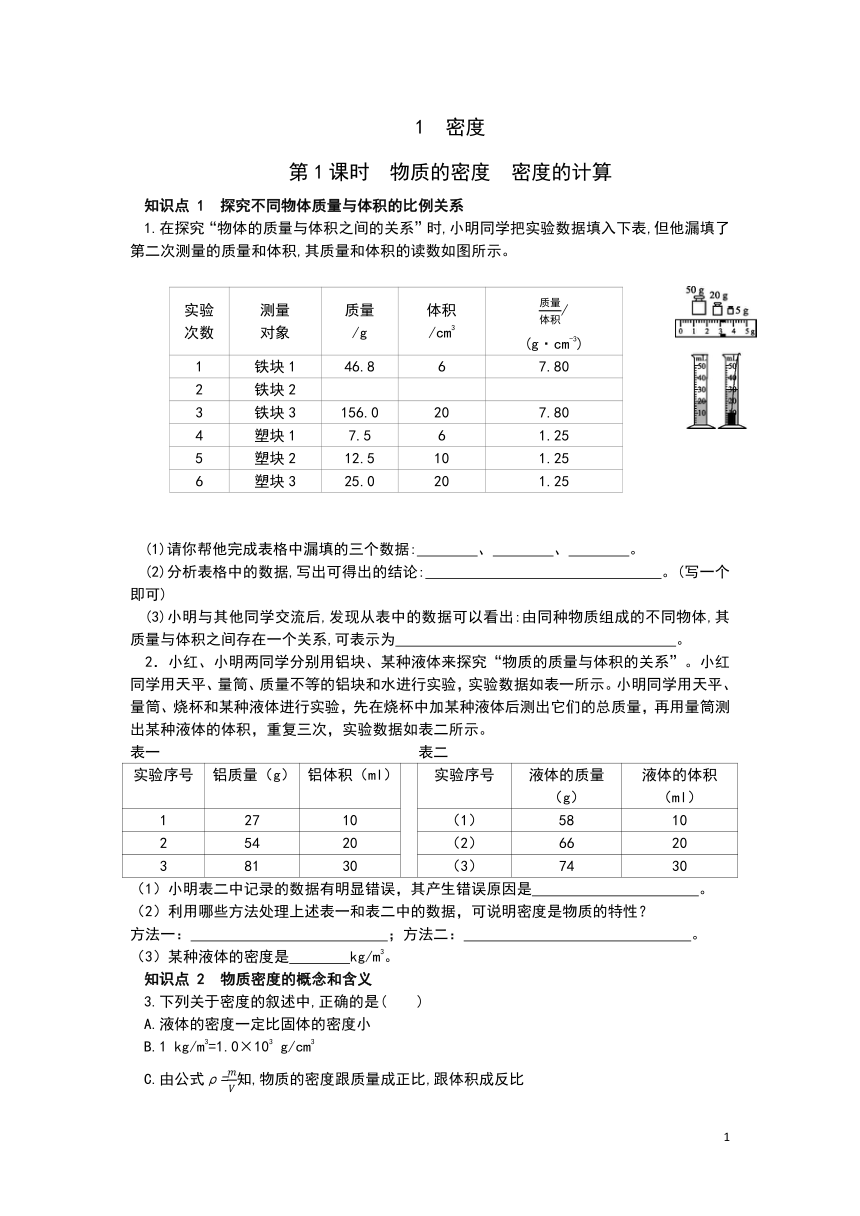 | |
| 格式 | zip | ||
| 文件大小 | 167.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 科学 | ||
| 更新时间 | 2021-10-04 12:00:09 | ||
图片预览



文档简介
1 密度
第1课时 物质的密度 密度的计算
知识点
1 探究不同物体质量与体积的比例关系
1.在探究“物体的质量与体积之间的关系”时,小明同学把实验数据填入下表,但他漏填了第二次测量的质量和体积,其质量和体积的读数如图所示。
实验
次数
测量
对象
质量
/g
体积
/cm3
/
(g·cm-3)
1
铁块1
46.8
6
7.80
2
铁块2
3
铁块3
156.0
20
7.80
4
塑块1
7.5
6
1.25
5
塑块2
12.5
10
1.25
6
塑块3
25.0
20
1.25
(1)请你帮他完成表格中漏填的三个数据: 、 、 。?
(2)分析表格中的数据,写出可得出的结论:
。(写一个即可)?
(3)小明与其他同学交流后,发现从表中的数据可以看出:由同种物质组成的不同物体,其质量与体积之间存在一个关系,可表示为
。?
2.小红、小明两同学分别用铝块、某种液体来探究“物质的质量与体积的关系”。小红同学用天平、量筒、质量不等的铝块和水进行实验,实验数据如表一所示。小明同学用天平、量筒、烧杯和某种液体进行实验,先在烧杯中加某种液体后测出它们的总质量,再用量筒测出某种液体的体积,重复三次,实验数据如表二所示。
表一
表二
实验序号
铝质量(g)
铝体积(ml)
实验序号
液体的质量(g)
液体的体积(ml)
1
27
10
(1)
58
10
2
54
20
(2)
66
20
3
81
30
(3)
74
30
(1)小明表二中记录的数据有明显错误,其产生错误原因是
。
(2)利用哪些方法处理上述表一和表二中的数据,可说明密度是物质的特性?
方法一:
;方法二:
。
(3)某种液体的密度是
kg/m3。
知识点
2 物质密度的概念和含义
3.下列关于密度的叙述中,正确的是( )
A.液体的密度一定比固体的密度小
B.1
kg/m3=1.0×103
g/cm3
C.由公式ρ=知,物质的密度跟质量成正比,跟体积成反比
D.不同物质的密度一般是不同的,因此可以用密度来鉴别物质
4.把边长为3
dm的正方体铁块,在相同的温度下压成长2
m、宽0.2
m的均匀铁皮,则下列说法中正确的是( )
A.铁块的形状、体积、质量和密度都变了
B.铁块的形状、体积改变,质量和密度不变
C.铁块的形状改变,体积、质量、密度都不变
D.铁块的质量和密度改变,体积和形状不变
5.分别由不同物质a、b、c组成的三个实心体,它们的体积和质量的关系如图所示,由图可知下列说法正确的是( )
A.a物质的密度最大
B.b物质的密度是1.0×103kg/m3
C.c物质的密度是a的两倍
D.b、c的密度与它们的质量、体积有关
6.
A、B、C三种物质的质量m与体积V的关系图线如图所示,A、B、C、三种物质的密度ρA、ρB、ρC和水的密度ρ水之间的关系( )
A.ρA>ρB>ρC且
ρA>ρ水
B.ρA>ρB>ρC且
ρC>ρ水
C.ρA<ρB<ρC且
ρA<ρ水
D.ρA<ρB<ρC且
ρA=ρ水
7.铜的密度是8.9×103kg/m3,它表示的物理意义是
。若将铜块截取二分之一,则剩余部分的密度为
kg/m3。
知识点
3 密度的计算
8.质量为8.1×103
kg的一块金属,它的体积为3
m3,则该金属块的密度是 ;若把它截去一半,则剩余部分的质量为 ,体积为 ,密度为 。?
9.如图所示,等臂天平处于平衡状态,则左盘物块的密度是( )
A.1.4
g/cm3
B.2.0
g/cm3
C.3.5
g/cm3
D.7.0
g/cm3
10.一名中学生的体积最接近( )
A.50
mm3
B.50
cm3
C.50
dm3
D.50
m3
11.飞机设计师为减轻飞机重力,将一实心钢制零件改为同形状的实心铝制零件,使其质量减小26kg,则所需铝的质量是(ρ钢=7.9×103kg/m3,ρ铝=2.7×103kg/m3)( )
A.12.5kg
B.13.5kg
C.27kg
D.39.5kg
12.一个薄壁的瓶子内装满某种液体,已知液体的质量为m。瓶底的面积为S,小明同学想测出液体的密度,他用刻度尺测得瓶子高度为L,然后倒出小半瓶液体(正立时近弯处),如图所示,测出液面高度L1,然后堵住瓶口,将瓶倒置,测出液面高度L2.则液体的密度为( )
A.
B.
C.
D.
能力提升
13.不漏气的氢气球由地面上升过程中,球内气体的质量与密度的变化情况是( )
A.质量增加,密度增加
B.质量不变,密度减小
C.质量减小,密度减小
D.质量不变,密度不变
14.关于质量和密度,下列说法中正确的是( )
A.植物种子带到太空后,质量变小,密度不变
B.一杯牛奶喝掉一半后,质量变小,密度不变
C.给车胎打气时,车胎内气体质量变大,密度不变
D.冰冻的矿泉水完全熔化后,质量变小,密度不变
15.阅读图表信息判断下面的说法,其中正确的是( )
常温常压下部分物质的密度/(kg·m-3)
金
19.3×103
水银
13.6×103
钢、铁
7.8×103
纯水
1.0×103
冰(0
℃)
0.9×103
植物油
0.9×103
干松木
0.5×103
酒精
0.8×103
A.固体的密度一定比液体的密度大
B.体积相同的植物油和酒精,酒精的质量大
C.同种物质在不同状态下,其密度一般不同
D.不同物质的密度一定不同
16.某钢瓶中装有氧气,瓶内气体密度为8
kg/m3,用去了其中的,则剩余气体的密度为( )
A.2
kg/m3
B.4
kg/m3
C.6
kg/m3
D.8
kg/m3
17.小花同学利用天平和量杯测量某种液体的密度时,记录的实验数据如下表。这种液体的密度和空量杯的质量分别是( )
液体与量杯的总质量m/g
30
50
70
液体的体积V/cm3
10
30
50
A.3.0×103
kg/m3 10
g
B.1.7×103
kg/m3 10
g
C.1.4×103
kg/m3 20
g
D.1.0×103
kg/m3 20
g
18.甲、乙两个机器零件的体积之比为2:3,质量之比为1:2,则甲、乙两个机器零件的密度之比为 ;如果甲、乙的密度之比为3:4,质量之比为1:1,则甲、乙的体积之比为 。?
19.已知一个空瓶子装满水后的总质量为300
g,在装满水的瓶子中放入一个小石块,溢出水后其总质量为320
g,取出石块后,剩余的水和瓶子的总质量为290
g(不计取出石块的过程中带走的水),则石块的质量为 g,石块的密度为 g/cm3。(ρ水=1.0×103
kg/m3)?
20.在探究质量与体积的关系时,小明找来大小不同的塑料块和某种液体做实验。
(1)图甲是小明在水平桌面上使用托盘天平的情景,他的错误是
。?
(2)改正错误后,小明正确操作,根据实验数据分别画出了塑料和该种液体的质量随体积变化的图像(如图乙所示)。
①分析图像可知:同种物质的不同物体,其质量与体积的比值 (填“相同”或“不同”),科学中将质量与体积的比值定义为密度;塑料的密度为 kg/m3。?
②往烧杯内倒入10
cm3的液体,用天平称出烧杯和液体的总质量,天平平衡时,右盘中砝码的质量及游码的位置如图丙所示,则烧杯和液体的总质量为 g。若烧杯内液体的体积为20
cm3,则烧杯和液体的总质量应为 g。?
21.有一质量为0.5
kg的空瓶,用它装满水,水和瓶的总质量是2
kg。
(1)酒精密度为0.8×103
kg/m3,若用此瓶改装酒精,最多能装下多少千克?
(2)若用此瓶改装另一种液体,装满时称得液体和瓶的总质量是3.2
kg,这种液体的密度是多少?
22.某高端矿泉水采用玻璃瓶瓶装。已知空瓶的质量为300g,容积为550mL,矿泉水的密度等于水的密度。
(1)求一满瓶该矿泉水的总质量(含瓶和水)为多少克?
(2)已知玻璃的密度为2.4×103kg/m3,求制作一个瓶需要玻璃的体积为多少cm3?
(3)已知用相同的瓶灌装同体积的酒精后,总质量为740g,求酒精的密度?
教师详解详析
1.(1)78.0 10 7.80
(2)同种物质,其质量与体积的比值相等
(3)ρ=
2.解:(1)表二中的质量记录的是杯和液体的总质量,应记录液体的质量;
(2)利用质量与体积比值、画质量与体积图象这两种方法可以说明密度是物质的特性;
(3)当液体和烧杯的总质量为58g时,ρV1+m杯=m1;
当液体和烧杯的总质量为66g时,ρV2+m杯=m2;
二式联立可得ρ===0.8g/cm3。
故答案为:
(1)测液体质量时,把烧杯质量也算进去了
(2)计算质量与体积的比值
做出质量与体积的图象
(3)0.8×103
3.D [解析]
常温常压下水银呈液态,但水银的密度比某些固体的密度大;1
g/cm3=
1.0×103
kg/m3;密度是物质的一种特性,其大小与物体的质量和体积无关;每种物质都有自己的密度,不同物质的密度一般是不同的,可以用密度来鉴别物质。
4.C
5.B.
6.A。
7.1m3的铜的质量是8.9×103kg、8.9×103。
8.2.7×103
kg/m3 4.05×103
kg
1.5
m3 2.7×103
kg/m3
[解析]
金属块的密度:ρ===2.7×103
kg/m3;截去一半,质量和体积都变为原来的,即剩余部分的质量为4.05×103
kg,体积为1.5
m3,密度为ρ===2.7×
103
kg/m3(或由于密度是物质的一种特性,与质量、体积无关,故密度仍为2.7×103
kg/m3)。
9.C [解析]
物块的密度:ρ=
==3.5
g/cm3。
10.C [解析]
一名中学生的质量约为50
kg,人的密度ρ≈ρ水=1.0×103
kg/m3,由ρ=可得,一名中学生的体积约为V===0.05
m3=50
dm3。
11.B。
12.A。
13.B [解析]
氢气球升空过程中,只是位置发生改变,球内气体的质量不变;由于大气压随高度的升高而减小,所以气球升空过程中,气球外的气压减小,球的体积增大,球内气体密度变小。
14.B [解析]
物体被带到太空只是改变了位置,质量、密度都不会改变;牛奶被喝掉一半,含有的物质变少了,质量自然变小,密度不变;打了气的车胎里气体增多,质量会增加,而它的体积却并没有发生明显的变化,密度会变大;冰熔化成水,状态发生了变化,质量不会改变,但密度会改变。
15.C
16.A
17.D [解析]
由表格数据可知,当液体体积V1=10
cm3时,液体和量杯的总质量m总1=30
g;当液体体积V2=30
cm3时,液体和量杯的总质量m总2=50
g;设量杯的质量为m杯,液体的密度为ρ,则:m总1=m1+m杯,30
g=ρV1+m杯①,m总2=m2+m杯,50
g=ρV2+m杯②,由①②得,ρ=1
g/cm3=
1.0×103
kg/m3,m杯=20
g。
18.3:4 4:3
[解析]
ρ甲?ρ乙=:=:=3:4;V甲':V乙'=:=:=4:3。
19.30 3
[解析]
石块的质量:m石=m溢总-m剩=320
g-290
g=30
g,石块排开水的质量:m排=m总-m剩=
300
g
—290
g=10
g,由
ρ=可得,石块的体积:
V石=V水===10
cm3,石块的密度:
ρ石===3
g/cm3。
20.(1)称量时调节平衡螺母
(2)①相同 1.2×103 ②37.4 45.4
[解析]
(1)天平正确的调节方法:将托盘天平放置在水平桌面上,将游码拨至标尺左端零刻度线处;调节横梁左右两端的平衡螺母,使横梁平衡;称量时不能再调节平衡螺母。
(2)①由图像可知,塑料(或液体)的质量和体积成正比,说明同种物质的不同物体,其质量与体积的比值相同;塑料的质量为30
g时,对应的体积为25
cm3,其密度:ρ塑料===1.2
g/cm3=1.2×103
kg/m3。
②烧杯和10
cm3该种液体的总质量:m总=20
g+10
g+5
g+2.4
g=37.4
g;该液体的密度:ρ===0.8
g/cm3,由ρ=得,10
cm3
该液体的质量:m液=ρV液=0.8
g/cm3×10
cm3=
8
g,同种液体密度相同,则20
cm3该液体的质量为16
g,故20
cm3该液体和烧杯的总质量:
m总'=37.4
g+8
g=45.4
g。
21.解:(1)瓶内水的质量:m水=m瓶+水-m瓶=2
kg-0.5
kg=1.5
kg,由ρ=得,瓶子的容积:V=
V水===1.5×10-3
m3,
瓶子能装酒精的质量:m酒精=ρ酒精V=0.8×103
kg/m3×1.5×10-3
m3=1.2
kg。
(2)瓶子中液体的质量:m液=m总-m瓶=3.2
kg-0.5
kg=2.7
kg,液体的密度:
ρ液===1.8×103
kg/m3。
22.解:(1)瓶子装满水后水的体积:
V水=V容=550mL=550cm3,
由ρ=可得水的质量:
m水=ρ水V水=1g/cm3×550cm3=550g,
一满瓶该矿泉水的总质量:
m总1=m水+m瓶=550g+300g=850g;
(2)玻璃的密度ρ玻璃=2.4×103kg/m3=2.4g/cm3,
由ρ=可得制作一个瓶需要玻璃的体积:
V玻璃===125cm3;
(3)酒精的质量:
m酒精=m总2﹣m瓶=740g﹣300g=440g,
酒精的体积:
V酒精=V容=550cm3,
酒精的密度:
ρ酒精===0.8g/cm3。
答:(1)一满瓶该矿泉水的总质量(含瓶和水)为850g;
(2)制作一个瓶需要玻璃的体积为125cm3;
(3)酒精的密度为0.8g/cm3。
1
第1课时 物质的密度 密度的计算
知识点
1 探究不同物体质量与体积的比例关系
1.在探究“物体的质量与体积之间的关系”时,小明同学把实验数据填入下表,但他漏填了第二次测量的质量和体积,其质量和体积的读数如图所示。
实验
次数
测量
对象
质量
/g
体积
/cm3
/
(g·cm-3)
1
铁块1
46.8
6
7.80
2
铁块2
3
铁块3
156.0
20
7.80
4
塑块1
7.5
6
1.25
5
塑块2
12.5
10
1.25
6
塑块3
25.0
20
1.25
(1)请你帮他完成表格中漏填的三个数据: 、 、 。?
(2)分析表格中的数据,写出可得出的结论:
。(写一个即可)?
(3)小明与其他同学交流后,发现从表中的数据可以看出:由同种物质组成的不同物体,其质量与体积之间存在一个关系,可表示为
。?
2.小红、小明两同学分别用铝块、某种液体来探究“物质的质量与体积的关系”。小红同学用天平、量筒、质量不等的铝块和水进行实验,实验数据如表一所示。小明同学用天平、量筒、烧杯和某种液体进行实验,先在烧杯中加某种液体后测出它们的总质量,再用量筒测出某种液体的体积,重复三次,实验数据如表二所示。
表一
表二
实验序号
铝质量(g)
铝体积(ml)
实验序号
液体的质量(g)
液体的体积(ml)
1
27
10
(1)
58
10
2
54
20
(2)
66
20
3
81
30
(3)
74
30
(1)小明表二中记录的数据有明显错误,其产生错误原因是
。
(2)利用哪些方法处理上述表一和表二中的数据,可说明密度是物质的特性?
方法一:
;方法二:
。
(3)某种液体的密度是
kg/m3。
知识点
2 物质密度的概念和含义
3.下列关于密度的叙述中,正确的是( )
A.液体的密度一定比固体的密度小
B.1
kg/m3=1.0×103
g/cm3
C.由公式ρ=知,物质的密度跟质量成正比,跟体积成反比
D.不同物质的密度一般是不同的,因此可以用密度来鉴别物质
4.把边长为3
dm的正方体铁块,在相同的温度下压成长2
m、宽0.2
m的均匀铁皮,则下列说法中正确的是( )
A.铁块的形状、体积、质量和密度都变了
B.铁块的形状、体积改变,质量和密度不变
C.铁块的形状改变,体积、质量、密度都不变
D.铁块的质量和密度改变,体积和形状不变
5.分别由不同物质a、b、c组成的三个实心体,它们的体积和质量的关系如图所示,由图可知下列说法正确的是( )
A.a物质的密度最大
B.b物质的密度是1.0×103kg/m3
C.c物质的密度是a的两倍
D.b、c的密度与它们的质量、体积有关
6.
A、B、C三种物质的质量m与体积V的关系图线如图所示,A、B、C、三种物质的密度ρA、ρB、ρC和水的密度ρ水之间的关系( )
A.ρA>ρB>ρC且
ρA>ρ水
B.ρA>ρB>ρC且
ρC>ρ水
C.ρA<ρB<ρC且
ρA<ρ水
D.ρA<ρB<ρC且
ρA=ρ水
7.铜的密度是8.9×103kg/m3,它表示的物理意义是
。若将铜块截取二分之一,则剩余部分的密度为
kg/m3。
知识点
3 密度的计算
8.质量为8.1×103
kg的一块金属,它的体积为3
m3,则该金属块的密度是 ;若把它截去一半,则剩余部分的质量为 ,体积为 ,密度为 。?
9.如图所示,等臂天平处于平衡状态,则左盘物块的密度是( )
A.1.4
g/cm3
B.2.0
g/cm3
C.3.5
g/cm3
D.7.0
g/cm3
10.一名中学生的体积最接近( )
A.50
mm3
B.50
cm3
C.50
dm3
D.50
m3
11.飞机设计师为减轻飞机重力,将一实心钢制零件改为同形状的实心铝制零件,使其质量减小26kg,则所需铝的质量是(ρ钢=7.9×103kg/m3,ρ铝=2.7×103kg/m3)( )
A.12.5kg
B.13.5kg
C.27kg
D.39.5kg
12.一个薄壁的瓶子内装满某种液体,已知液体的质量为m。瓶底的面积为S,小明同学想测出液体的密度,他用刻度尺测得瓶子高度为L,然后倒出小半瓶液体(正立时近弯处),如图所示,测出液面高度L1,然后堵住瓶口,将瓶倒置,测出液面高度L2.则液体的密度为( )
A.
B.
C.
D.
能力提升
13.不漏气的氢气球由地面上升过程中,球内气体的质量与密度的变化情况是( )
A.质量增加,密度增加
B.质量不变,密度减小
C.质量减小,密度减小
D.质量不变,密度不变
14.关于质量和密度,下列说法中正确的是( )
A.植物种子带到太空后,质量变小,密度不变
B.一杯牛奶喝掉一半后,质量变小,密度不变
C.给车胎打气时,车胎内气体质量变大,密度不变
D.冰冻的矿泉水完全熔化后,质量变小,密度不变
15.阅读图表信息判断下面的说法,其中正确的是( )
常温常压下部分物质的密度/(kg·m-3)
金
19.3×103
水银
13.6×103
钢、铁
7.8×103
纯水
1.0×103
冰(0
℃)
0.9×103
植物油
0.9×103
干松木
0.5×103
酒精
0.8×103
A.固体的密度一定比液体的密度大
B.体积相同的植物油和酒精,酒精的质量大
C.同种物质在不同状态下,其密度一般不同
D.不同物质的密度一定不同
16.某钢瓶中装有氧气,瓶内气体密度为8
kg/m3,用去了其中的,则剩余气体的密度为( )
A.2
kg/m3
B.4
kg/m3
C.6
kg/m3
D.8
kg/m3
17.小花同学利用天平和量杯测量某种液体的密度时,记录的实验数据如下表。这种液体的密度和空量杯的质量分别是( )
液体与量杯的总质量m/g
30
50
70
液体的体积V/cm3
10
30
50
A.3.0×103
kg/m3 10
g
B.1.7×103
kg/m3 10
g
C.1.4×103
kg/m3 20
g
D.1.0×103
kg/m3 20
g
18.甲、乙两个机器零件的体积之比为2:3,质量之比为1:2,则甲、乙两个机器零件的密度之比为 ;如果甲、乙的密度之比为3:4,质量之比为1:1,则甲、乙的体积之比为 。?
19.已知一个空瓶子装满水后的总质量为300
g,在装满水的瓶子中放入一个小石块,溢出水后其总质量为320
g,取出石块后,剩余的水和瓶子的总质量为290
g(不计取出石块的过程中带走的水),则石块的质量为 g,石块的密度为 g/cm3。(ρ水=1.0×103
kg/m3)?
20.在探究质量与体积的关系时,小明找来大小不同的塑料块和某种液体做实验。
(1)图甲是小明在水平桌面上使用托盘天平的情景,他的错误是
。?
(2)改正错误后,小明正确操作,根据实验数据分别画出了塑料和该种液体的质量随体积变化的图像(如图乙所示)。
①分析图像可知:同种物质的不同物体,其质量与体积的比值 (填“相同”或“不同”),科学中将质量与体积的比值定义为密度;塑料的密度为 kg/m3。?
②往烧杯内倒入10
cm3的液体,用天平称出烧杯和液体的总质量,天平平衡时,右盘中砝码的质量及游码的位置如图丙所示,则烧杯和液体的总质量为 g。若烧杯内液体的体积为20
cm3,则烧杯和液体的总质量应为 g。?
21.有一质量为0.5
kg的空瓶,用它装满水,水和瓶的总质量是2
kg。
(1)酒精密度为0.8×103
kg/m3,若用此瓶改装酒精,最多能装下多少千克?
(2)若用此瓶改装另一种液体,装满时称得液体和瓶的总质量是3.2
kg,这种液体的密度是多少?
22.某高端矿泉水采用玻璃瓶瓶装。已知空瓶的质量为300g,容积为550mL,矿泉水的密度等于水的密度。
(1)求一满瓶该矿泉水的总质量(含瓶和水)为多少克?
(2)已知玻璃的密度为2.4×103kg/m3,求制作一个瓶需要玻璃的体积为多少cm3?
(3)已知用相同的瓶灌装同体积的酒精后,总质量为740g,求酒精的密度?
教师详解详析
1.(1)78.0 10 7.80
(2)同种物质,其质量与体积的比值相等
(3)ρ=
2.解:(1)表二中的质量记录的是杯和液体的总质量,应记录液体的质量;
(2)利用质量与体积比值、画质量与体积图象这两种方法可以说明密度是物质的特性;
(3)当液体和烧杯的总质量为58g时,ρV1+m杯=m1;
当液体和烧杯的总质量为66g时,ρV2+m杯=m2;
二式联立可得ρ===0.8g/cm3。
故答案为:
(1)测液体质量时,把烧杯质量也算进去了
(2)计算质量与体积的比值
做出质量与体积的图象
(3)0.8×103
3.D [解析]
常温常压下水银呈液态,但水银的密度比某些固体的密度大;1
g/cm3=
1.0×103
kg/m3;密度是物质的一种特性,其大小与物体的质量和体积无关;每种物质都有自己的密度,不同物质的密度一般是不同的,可以用密度来鉴别物质。
4.C
5.B.
6.A。
7.1m3的铜的质量是8.9×103kg、8.9×103。
8.2.7×103
kg/m3 4.05×103
kg
1.5
m3 2.7×103
kg/m3
[解析]
金属块的密度:ρ===2.7×103
kg/m3;截去一半,质量和体积都变为原来的,即剩余部分的质量为4.05×103
kg,体积为1.5
m3,密度为ρ===2.7×
103
kg/m3(或由于密度是物质的一种特性,与质量、体积无关,故密度仍为2.7×103
kg/m3)。
9.C [解析]
物块的密度:ρ=
==3.5
g/cm3。
10.C [解析]
一名中学生的质量约为50
kg,人的密度ρ≈ρ水=1.0×103
kg/m3,由ρ=可得,一名中学生的体积约为V===0.05
m3=50
dm3。
11.B。
12.A。
13.B [解析]
氢气球升空过程中,只是位置发生改变,球内气体的质量不变;由于大气压随高度的升高而减小,所以气球升空过程中,气球外的气压减小,球的体积增大,球内气体密度变小。
14.B [解析]
物体被带到太空只是改变了位置,质量、密度都不会改变;牛奶被喝掉一半,含有的物质变少了,质量自然变小,密度不变;打了气的车胎里气体增多,质量会增加,而它的体积却并没有发生明显的变化,密度会变大;冰熔化成水,状态发生了变化,质量不会改变,但密度会改变。
15.C
16.A
17.D [解析]
由表格数据可知,当液体体积V1=10
cm3时,液体和量杯的总质量m总1=30
g;当液体体积V2=30
cm3时,液体和量杯的总质量m总2=50
g;设量杯的质量为m杯,液体的密度为ρ,则:m总1=m1+m杯,30
g=ρV1+m杯①,m总2=m2+m杯,50
g=ρV2+m杯②,由①②得,ρ=1
g/cm3=
1.0×103
kg/m3,m杯=20
g。
18.3:4 4:3
[解析]
ρ甲?ρ乙=:=:=3:4;V甲':V乙'=:=:=4:3。
19.30 3
[解析]
石块的质量:m石=m溢总-m剩=320
g-290
g=30
g,石块排开水的质量:m排=m总-m剩=
300
g
—290
g=10
g,由
ρ=可得,石块的体积:
V石=V水===10
cm3,石块的密度:
ρ石===3
g/cm3。
20.(1)称量时调节平衡螺母
(2)①相同 1.2×103 ②37.4 45.4
[解析]
(1)天平正确的调节方法:将托盘天平放置在水平桌面上,将游码拨至标尺左端零刻度线处;调节横梁左右两端的平衡螺母,使横梁平衡;称量时不能再调节平衡螺母。
(2)①由图像可知,塑料(或液体)的质量和体积成正比,说明同种物质的不同物体,其质量与体积的比值相同;塑料的质量为30
g时,对应的体积为25
cm3,其密度:ρ塑料===1.2
g/cm3=1.2×103
kg/m3。
②烧杯和10
cm3该种液体的总质量:m总=20
g+10
g+5
g+2.4
g=37.4
g;该液体的密度:ρ===0.8
g/cm3,由ρ=得,10
cm3
该液体的质量:m液=ρV液=0.8
g/cm3×10
cm3=
8
g,同种液体密度相同,则20
cm3该液体的质量为16
g,故20
cm3该液体和烧杯的总质量:
m总'=37.4
g+8
g=45.4
g。
21.解:(1)瓶内水的质量:m水=m瓶+水-m瓶=2
kg-0.5
kg=1.5
kg,由ρ=得,瓶子的容积:V=
V水===1.5×10-3
m3,
瓶子能装酒精的质量:m酒精=ρ酒精V=0.8×103
kg/m3×1.5×10-3
m3=1.2
kg。
(2)瓶子中液体的质量:m液=m总-m瓶=3.2
kg-0.5
kg=2.7
kg,液体的密度:
ρ液===1.8×103
kg/m3。
22.解:(1)瓶子装满水后水的体积:
V水=V容=550mL=550cm3,
由ρ=可得水的质量:
m水=ρ水V水=1g/cm3×550cm3=550g,
一满瓶该矿泉水的总质量:
m总1=m水+m瓶=550g+300g=850g;
(2)玻璃的密度ρ玻璃=2.4×103kg/m3=2.4g/cm3,
由ρ=可得制作一个瓶需要玻璃的体积:
V玻璃===125cm3;
(3)酒精的质量:
m酒精=m总2﹣m瓶=740g﹣300g=440g,
酒精的体积:
V酒精=V容=550cm3,
酒精的密度:
ρ酒精===0.8g/cm3。
答:(1)一满瓶该矿泉水的总质量(含瓶和水)为850g;
(2)制作一个瓶需要玻璃的体积为125cm3;
(3)酒精的密度为0.8g/cm3。
1
同课章节目录
- 第1章 运动和力
- 1 机械运动
- 2 力
- 3 几种常见的力
- 4 运动和力
- 5 二力平衡的条件
- 第2章 压力 压强
- 1 压强
- 2 液体内部的压强
- 3 大气压强
- 4 流体的压强与流速的关系
- 第3章 浮力
- 1 密度
- 2 浮力
- 3 阿基米德原理
- 4 物体浮沉条件及其应用
- 第4章 植物的物质和能量的转化
- 1 绿色开花植物的营养器官
- 2 水在植物体中的代谢
- 3 无机盐在植物体内的代谢
- 4 植物的光合作用和呼吸作用
- 第5章 人体的物质和能量的转化
- 1 食物的消化和吸收
- 2 人体的呼吸
- 3 人体内的物质运输
- 4 人体的排泄
- 5 人体生命活动过程中物质和能量的转化
- 第6章 物质的构成
- 1 构成物质的微粒
- 2 元素
- 3 物质的分类
- 4 化学式
- 5 固态物质
