2021—2022学年北师大版数学九年级上册 4.1 成比例线段(第一课时)课件 (共30张)
文档属性
| 名称 | 2021—2022学年北师大版数学九年级上册 4.1 成比例线段(第一课时)课件 (共30张) |  | |
| 格式 | ppt | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-18 19:41:35 | ||
图片预览








文档简介
(共30张PPT)
全等形
指能够完全重合的两个图形,即它们的形状和大小完全相同.
复习回顾
情景引入
实际生活中我们经常会看到许多形状相同的图形。
如图,用同一张底片洗出的不同尺寸
的照片中,汽车的形状还相同吗?
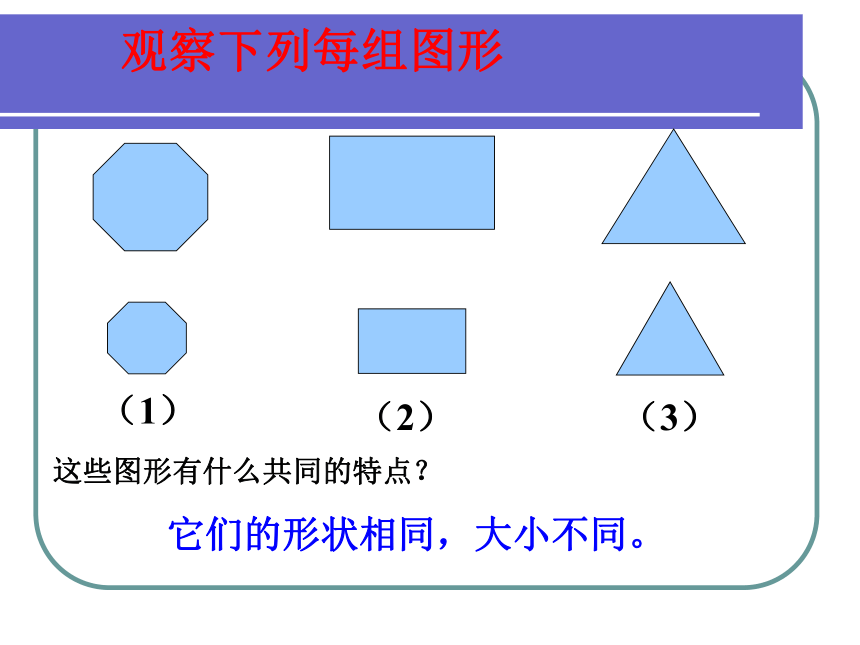
观察下列每组图形
(1)
(2)
(3)
这些图形有什么共同的特点?
它们的形状相同,大小不同。
已知:在图上黄果树瀑布的高约30cm,小颖的高约2cm,那么这两条线段的长度比是多少?
黄果树大瀑布
小颖
定义:
如果选用一个长度单位量得两条线段AB,CD的长度分别是m,n。那么这两条线段的比AB:CD=m:n,或写成
其中线段AB,CD分别叫做这个线段比的前项和后项.
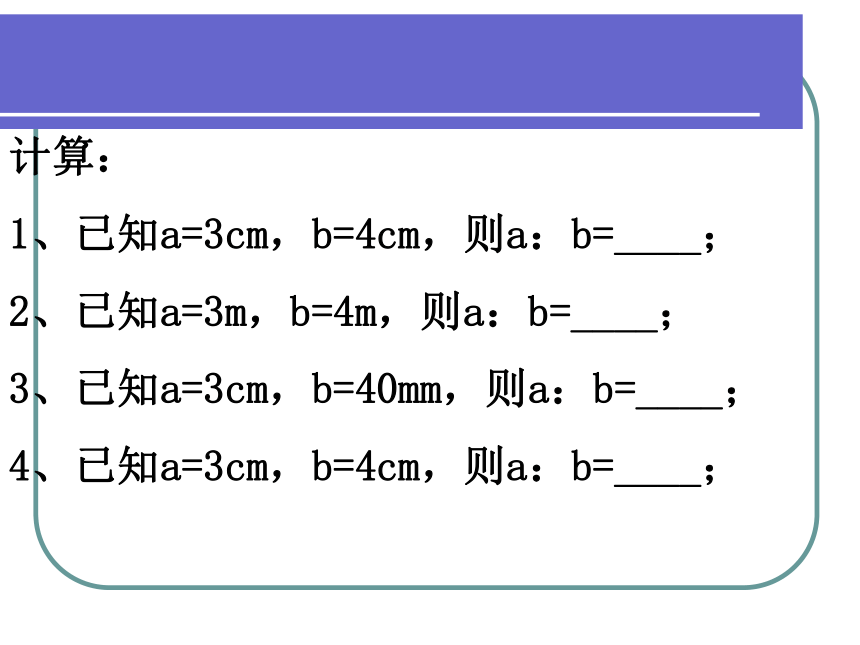
计算:
1、已知a=3cm,b=4cm,则a:b=____;
2、已知a=3m,b=4m,则a:b=____;
3、已知a=3cm,b=40mm,则a:b=____;
4、已知a=3cm,b=4cm,则a:b=____;
1.两条线段的比就是长度的比,它没有单位;
如何理解两条线段的比?
4.求两条线段的比时,如果单位不同,那么必须先化成同一单位,再求它们的比。
3.两条线段比与所选的长度单位无关;
2.两条线段的比是有顺序的;
判断一下:
①已知:线段a=20mm,b=3cm,则
②已知:线段a=1cm,b=2cm,则
③已知:线段a=3mm,b=2mm,则
练习2:
(1)a=2m
,
b=0.4m
;
(2)a=6cm
,
b=6m
;
(3)a=50mm
,
b=6cm
;
(4)a=3m
,
b=10mm
.
求下列各题中
a:b
的值
A
B
C
A′
B′
C′
1
1
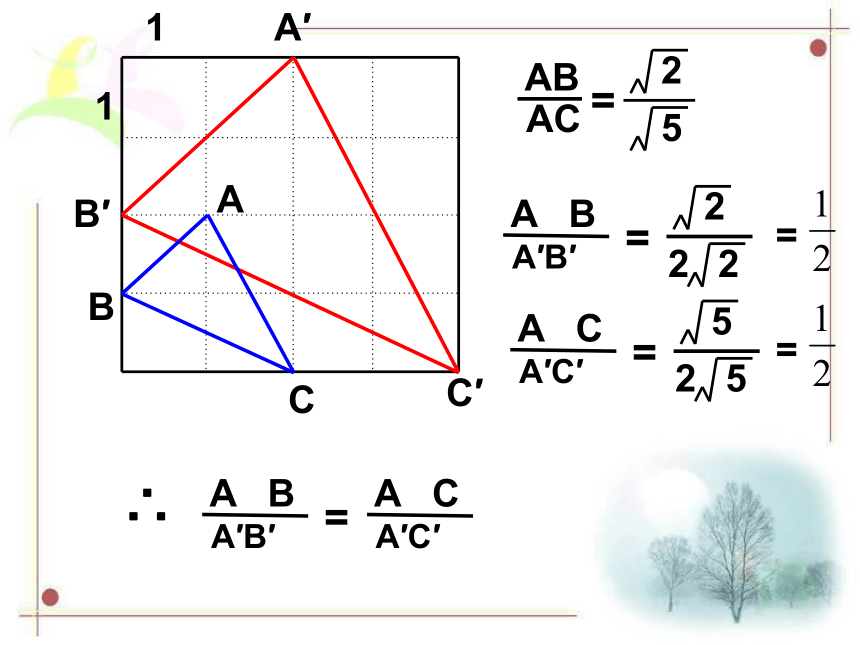
AB
AC
=
5
2
A
B
A′B′
=
2
2
2
=
A
C
A′C′
=
5
5
2
=
∴
A
B
A′B′
=
A
C
A′C′
在四条线段
a、b、c、d
中,如果
a
:b=
c
:d
,那么这四条线段a、b、c、d
叫做成比例线段,
简称比例线段.
外项
外项
内项
内项
a
:b
=
c
:d.
外项
内项
a、b、c
的第四比例项
成比例线段:
说出下列比例式中的比例内项、比例外项
和第四比例项:
p
q
=
f
s
(1)
(2)
(x+1)
:
x
=
(1+-)
:
1
1
x
比例线段
1、单位统一
2、顺序性:
称a,b,c,d成比例
称a,
d,c,b
成比例
例2判断下列线段a、b、c、d是否是成比例线段:
(1)a=4,b=6,c=5,d=10;
解
(1) ∵
∴ 线段a、b、c、d不是成比例线段.
,
,
∴
,
(2)a=2,b=
,c=
,d=
.
(2) ∵
,
∴
∴ 线段a、b、c、d是成比例线段.
解:
1.判断下列线段是否是成比例线段:
(1)a=2cm,b=4cm,c=3m,d=6m;
(2)a=0.8,b=3,c=1,d=2.4.
如何快速地判断线段是否成比例?
将线段从小到大的顺序排列,计算第一和第二之比,第三和第四之比,看他们的比值是否相同
(2)a=0.8,c=1,d=2.4,b=3
所以a,c,d,b成比例线段
探索新知
两内项之积等于两外项之积
比例的基本性质
应用新知
1、求下列比例式中的x值。
(1)4:3=5:x,那么x=
,
(2)3:x=6:12,那么x=
。
2、根据下列条件,求a:b的值.
已知
ad=bc,你能得到哪些比例式?
对调内项,
比例仍成立!
对调外项,
比例仍成立!
a
b
c
d
=
b
a
d
c
=
b
d
a
c
=
c
d
a
b
=
d
b
c
a
=
a
c
b
d
=
c
a
d
b
=
d
c
b
a
=
勤于动脑
当比例内项相等时,即
那么b叫作a,c的比例中项
由此得出
1、若a,b,c,d成比例,且a=2,b=3,c=4,则d=
。
2、已知线段a=3,b=12,线段c是线段a,b的比例中项,则C=
。
6
6
求:图上距离与实际距离的比
例1
图上距离
地图的比例尺=-----------
实际距离
已知:一张地图的比例尺1:32000000
量得北京到上海的图上距离大约为3.5cm,
求北京到上海的实际距离大约是多少km?
C
A
B
想一想:AB=4这个条件如果去掉,此题能不能做?
A
B
4
已知:△ABC中,D、E分别是AB、AC的中点,那么线段AD、AB、DE、BC是否成比例线段?为什么?
A
B
C
D
E
现在有一棵很高的古树,欲测出它的高度,但又不能爬到树尖上去直接测量,你有什么好的方法吗?
A
B
C
A’
B’
C’
在相同时刻的物高与影长成比例
课外拓展
全等形
指能够完全重合的两个图形,即它们的形状和大小完全相同.
复习回顾
情景引入
实际生活中我们经常会看到许多形状相同的图形。
如图,用同一张底片洗出的不同尺寸
的照片中,汽车的形状还相同吗?
观察下列每组图形
(1)
(2)
(3)
这些图形有什么共同的特点?
它们的形状相同,大小不同。
已知:在图上黄果树瀑布的高约30cm,小颖的高约2cm,那么这两条线段的长度比是多少?
黄果树大瀑布
小颖
定义:
如果选用一个长度单位量得两条线段AB,CD的长度分别是m,n。那么这两条线段的比AB:CD=m:n,或写成
其中线段AB,CD分别叫做这个线段比的前项和后项.
计算:
1、已知a=3cm,b=4cm,则a:b=____;
2、已知a=3m,b=4m,则a:b=____;
3、已知a=3cm,b=40mm,则a:b=____;
4、已知a=3cm,b=4cm,则a:b=____;
1.两条线段的比就是长度的比,它没有单位;
如何理解两条线段的比?
4.求两条线段的比时,如果单位不同,那么必须先化成同一单位,再求它们的比。
3.两条线段比与所选的长度单位无关;
2.两条线段的比是有顺序的;
判断一下:
①已知:线段a=20mm,b=3cm,则
②已知:线段a=1cm,b=2cm,则
③已知:线段a=3mm,b=2mm,则
练习2:
(1)a=2m
,
b=0.4m
;
(2)a=6cm
,
b=6m
;
(3)a=50mm
,
b=6cm
;
(4)a=3m
,
b=10mm
.
求下列各题中
a:b
的值
A
B
C
A′
B′
C′
1
1
AB
AC
=
5
2
A
B
A′B′
=
2
2
2
=
A
C
A′C′
=
5
5
2
=
∴
A
B
A′B′
=
A
C
A′C′
在四条线段
a、b、c、d
中,如果
a
:b=
c
:d
,那么这四条线段a、b、c、d
叫做成比例线段,
简称比例线段.
外项
外项
内项
内项
a
:b
=
c
:d.
外项
内项
a、b、c
的第四比例项
成比例线段:
说出下列比例式中的比例内项、比例外项
和第四比例项:
p
q
=
f
s
(1)
(2)
(x+1)
:
x
=
(1+-)
:
1
1
x
比例线段
1、单位统一
2、顺序性:
称a,b,c,d成比例
称a,
d,c,b
成比例
例2判断下列线段a、b、c、d是否是成比例线段:
(1)a=4,b=6,c=5,d=10;
解
(1) ∵
∴ 线段a、b、c、d不是成比例线段.
,
,
∴
,
(2)a=2,b=
,c=
,d=
.
(2) ∵
,
∴
∴ 线段a、b、c、d是成比例线段.
解:
1.判断下列线段是否是成比例线段:
(1)a=2cm,b=4cm,c=3m,d=6m;
(2)a=0.8,b=3,c=1,d=2.4.
如何快速地判断线段是否成比例?
将线段从小到大的顺序排列,计算第一和第二之比,第三和第四之比,看他们的比值是否相同
(2)a=0.8,c=1,d=2.4,b=3
所以a,c,d,b成比例线段
探索新知
两内项之积等于两外项之积
比例的基本性质
应用新知
1、求下列比例式中的x值。
(1)4:3=5:x,那么x=
,
(2)3:x=6:12,那么x=
。
2、根据下列条件,求a:b的值.
已知
ad=bc,你能得到哪些比例式?
对调内项,
比例仍成立!
对调外项,
比例仍成立!
a
b
c
d
=
b
a
d
c
=
b
d
a
c
=
c
d
a
b
=
d
b
c
a
=
a
c
b
d
=
c
a
d
b
=
d
c
b
a
=
勤于动脑
当比例内项相等时,即
那么b叫作a,c的比例中项
由此得出
1、若a,b,c,d成比例,且a=2,b=3,c=4,则d=
。
2、已知线段a=3,b=12,线段c是线段a,b的比例中项,则C=
。
6
6
求:图上距离与实际距离的比
例1
图上距离
地图的比例尺=-----------
实际距离
已知:一张地图的比例尺1:32000000
量得北京到上海的图上距离大约为3.5cm,
求北京到上海的实际距离大约是多少km?
C
A
B
想一想:AB=4这个条件如果去掉,此题能不能做?
A
B
4
已知:△ABC中,D、E分别是AB、AC的中点,那么线段AD、AB、DE、BC是否成比例线段?为什么?
A
B
C
D
E
现在有一棵很高的古树,欲测出它的高度,但又不能爬到树尖上去直接测量,你有什么好的方法吗?
A
B
C
A’
B’
C’
在相同时刻的物高与影长成比例
课外拓展
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
