2021--2022学年北师大版九年级数学上册 1.3 正方形的性质与判定 课件 (共21张)
文档属性
| 名称 | 2021--2022学年北师大版九年级数学上册 1.3 正方形的性质与判定 课件 (共21张) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-18 19:52:35 | ||
图片预览



文档简介
(共21张PPT)
1.3
正方形的性质与判定
学习目标
1.掌握正方形的判定方法;会运用正方形的判定条件进行有关的论证和计算.
2.理解特殊的平行四边形之间的内在联系,形成辨证看问题的观点.
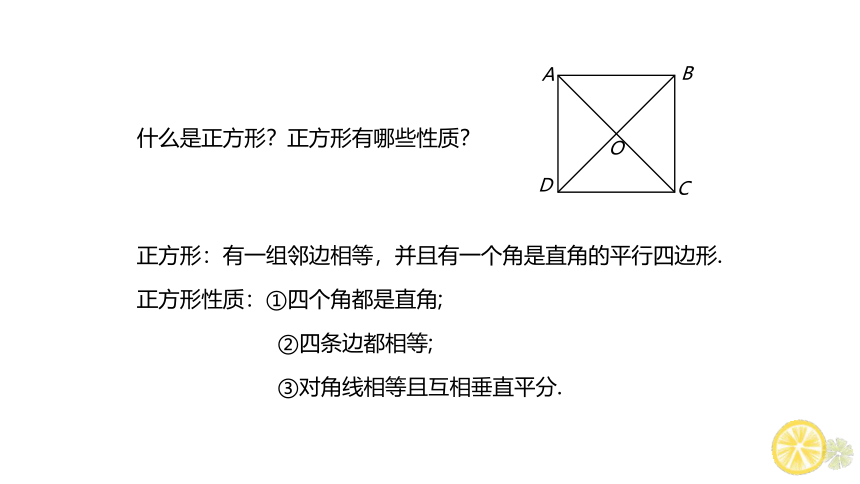
什么是正方形?正方形有哪些性质?
正方形:有一组邻边相等,并且有一个角是直角的平行四边形.
正方形性质:①四个角都是直角;
②四条边都相等;
③对角线相等且互相垂直平分.
A
B
C
D
O
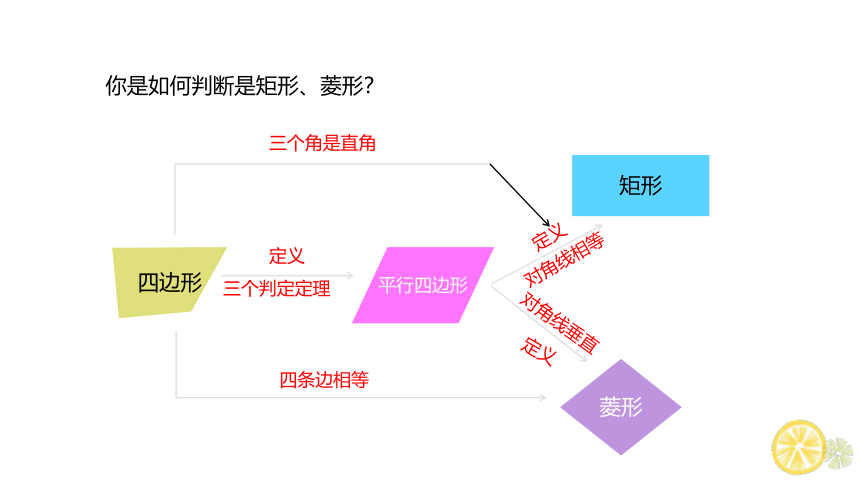
你是如何判断是矩形、菱形?
平行四边形
矩形
菱形
四边形
三个角是直角
四条边相等
定义
三个判定定理
定义
对角线相等
定义
对角线垂直
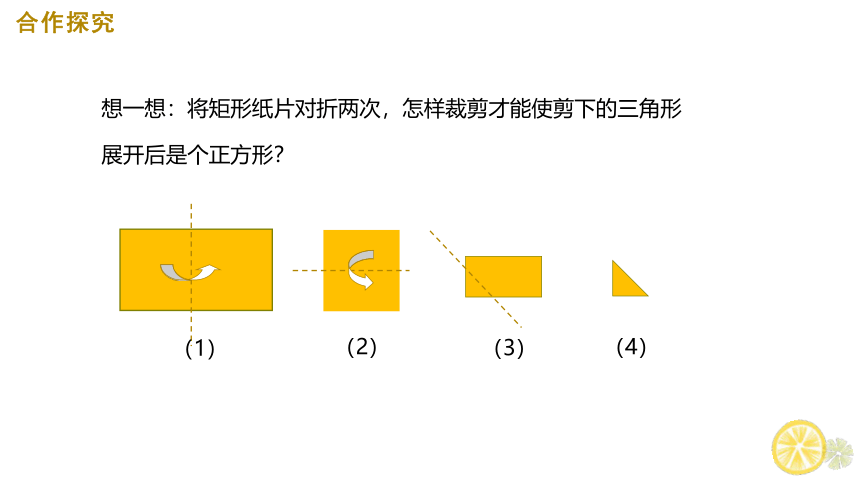
合作探究
想一想:将矩形纸片对折两次,怎样裁剪才能使剪下的三角形
展开后是个正方形?
(1)
(2)
(3)
(4)
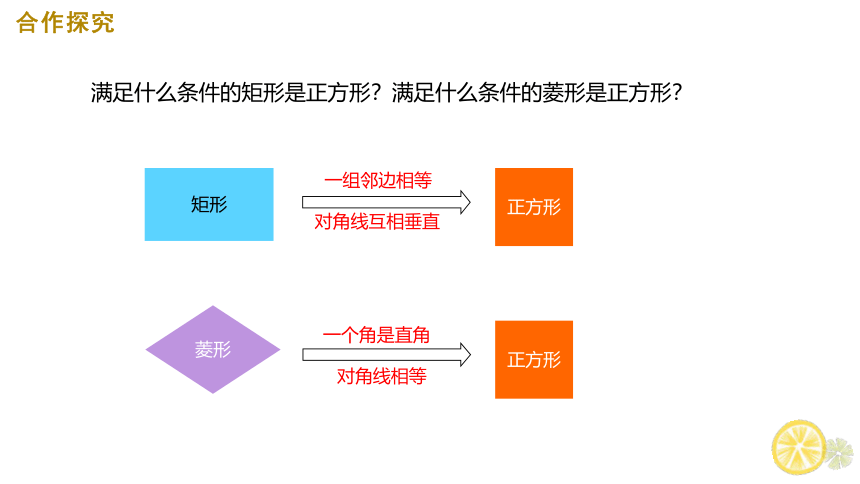
合作探究
满足什么条件的矩形是正方形?满足什么条件的菱形是正方形?
矩形
正方形
一组邻边相等
对角线互相垂直
菱形
正方形
一个角是直角
对角线相等
新课讲授
正方形判定定理
1.对角线相等的菱形是正方形.
2.对角线垂直的矩形是正方形.
3.有一个角是直角的菱形是正方形.
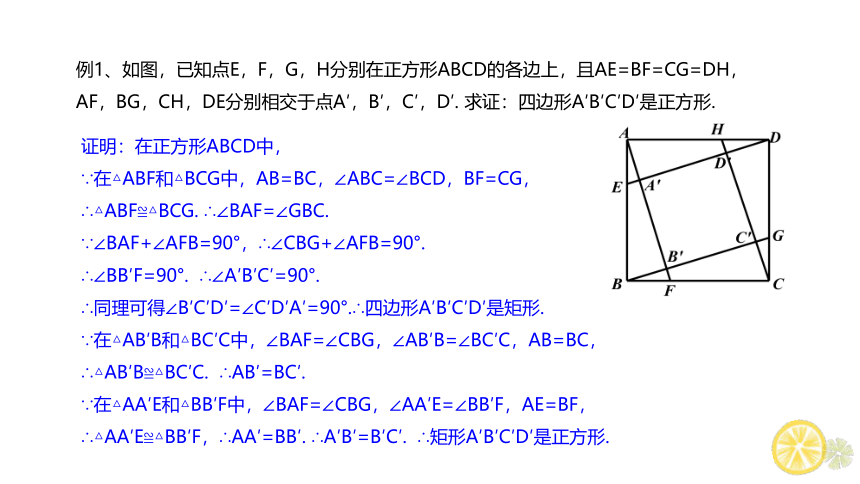
例1、如图,已知点E,F,G,H分别在正方形ABCD的各边上,且AE=BF=CG=DH,AF,BG,CH,DE分别相交于点A′,B′,C′,D′.
求证:四边形A′B′C′D′是正方形.
证明:在正方形ABCD中,
∵在△ABF和△BCG中,AB=BC,∠ABC=∠BCD,BF=CG,
∴△ABF≌△BCG.
∴∠BAF=∠GBC.
∵∠BAF+∠AFB=90°,∴∠CBG+∠AFB=90°.
∴∠BB′F=90°.
∴∠A′B′C′=90°.
∴同理可得∠B′C′D′=∠C′D′A′=90°.∴四边形A′B′C′D′是矩形.
∵在△AB′B和△BC′C中,∠BAF=∠CBG,∠AB′B=∠BC′C,AB=BC,
∴△AB′B≌△BC′C.
∴AB′=BC′.
∵在△AA′E和△BB′F中,∠BAF=∠CBG,∠AA′E=∠BB′F,AE=BF,
∴△AA′E≌△BB′F,∴AA′=BB′.
∴A′B′=B′C′.
∴矩形A′B′C′D′是正方形.
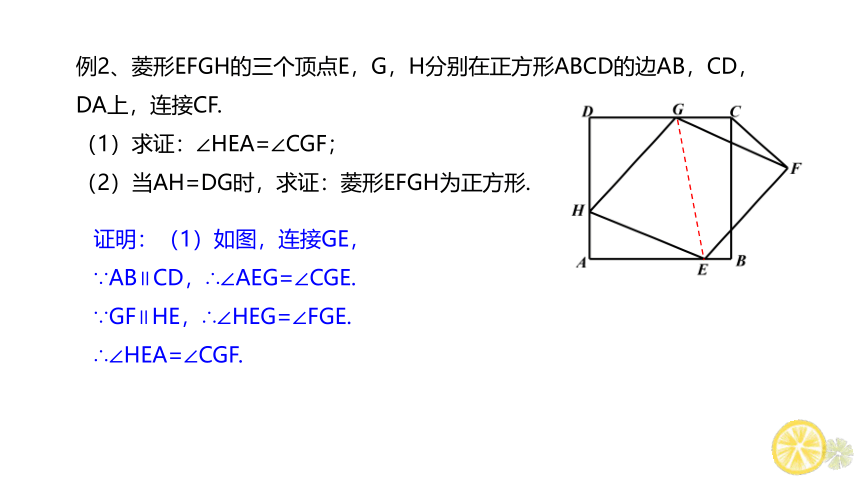
例2、菱形EFGH的三个顶点E,G,H分别在正方形ABCD的边AB,CD,DA上,连接CF.
(1)求证:∠HEA=∠CGF;
(2)当AH=DG时,求证:菱形EFGH为正方形.
证明:(1)如图,连接GE,
∵AB∥CD,∴∠AEG=∠CGE.
∵GF∥HE,∴∠HEG=∠FGE.
∴∠HEA=∠CGF.
例2、菱形EFGH的三个顶点E,G,H分别在正方形ABCD的边AB,CD,DA上,连接CF.
(1)求证:∠HEA=∠CGF;
(2)当AH=DG时,求证:菱形EFGH为正方形.
(2)∵四边形ABCD是正方形,∴∠D=∠A=90°.
∵四边形EFGH是菱形,∴HG=HE.
在Rt△HAE和Rt△GDH中,AH=DG,HE=HG,
∴Rt△HAE≌Rt△GDH(HL).
∴∠AHE=∠DGH.
又∠DHG+∠DGH=90°,
∴∠DHG+∠AHE=90°.∴∠GHE=90°.
∴菱形EFGH为正方形.
合作探究
做一做:顺次连接任意四边形各边中点所得的四边形是平行四边形.顺次连接矩形、正方形各边中点能得到怎样的特殊平行四边形?
A
B
C
D
A
B
C
D
A
B
C
D
矩形
正方形
任意四边形
平行四边形
菱形
正方形
E
F
G
H
E
F
G
H
E
F
G
H
新课讲授
常见中点四边形比较
名称
任意四边形
矩形
菱形
正方形
对角线特点
既不垂直
也不相等
不垂直,仅相等
垂直但不相等
垂直且相等
中点四边形
基本图形
A
B
C
D
E
F
G
H
平行四边形
A
B
C
D
E
F
G
H
菱形
A
B
C
D
E
F
G
H
A
B
C
D
E
F
G
H
矩形
正方形
例3、如图,在矩形ABCD中,M、N分别是AD、BC的中点,E、F分别是边BM、CM的中点,当AB∶AD=________时,四边形MENF是正方形.
解:当AB∶AD=1∶2时,四边形MENF是正方形.
∵AB∶AD=1∶2,AM=DM,AB=CD,∴AB=AM=DM=DC,
∵∠A=∠D=90°,
∴∠ABM=∠AMB=∠DMC=∠DCM=45°,∴∠BMC=90°.
∵四边形ABCD是矩形,∴∠ABC=∠DCB=90°,
∴∠MBC=∠MCB=45°,∴BM=CM.
∵N、E、F分别是BC、BM、CM的中点,
∴BE=CF=ME=MF,NF∥BM,NE∥CM,
∴四边形MENF是平行四边形,
∵ME=MF,∠BMC=90°,
∴四边形MENF是正方形.
随堂练习
1.在四边形ABCD中,O是对角线的交点,能判定这个四边形是正方形的条件是?( )
A.AC=BD,AB//CD
B.AD∥BC,∠A=∠C
C.AO=BO=CO=DO,
AC⊥BD
D.AO=CO,BO=DO,
AB=BC
C
A
B
C
D
O
随堂练习
2.如图所示,在四边形ABCD中,AB=BC=CD=DA,对角线AC与BD相交于点O.若不添加任何字母与辅助线,要使得四边形ABCD是正方形,则还需添加的一个条件是___________________.
AC=BD(答案不唯一)
A
B
C
D
O
随堂练习
3.将五个边长都为2
cm的正方形按如图所示摆放,点A、B、C、D分别是四个正方形的中心,则图中四块阴影面积的和为?( )
A.2
cm2 ????B.4
cm2 ????C.6
cm2 ????D.8
cm2
B
随堂练习
4.如图所示,在ABCD中,对角线AC,BD交于点O,E是BD延长线上的点,且EA=EC.
(1)求证:四边形ABCD是菱形;
(2)若∠DAC=∠EAD+∠AED,求证:四边形ABCD是正方形.
证明:(1)∵四边形ABCD是平行四边形,
∴AO=CO=AC,
∵EA=EC,
∴EO⊥AC,即BD⊥AC,
∴平行四边形ABCD是菱形.
随堂练习
4.如图所示,在ABCD中,对角线AC,BD交于点O,E是BD延长线上的点,且EA=EC.
(1)求证:四边形ABCD是菱形;
(2)若∠DAC=∠EAD+∠AED,求证:四边形ABCD是正方形.
(2)∵∠1=∠EAD+∠AED,
∠DAC=∠EAD+∠AED,
∴∠1=∠DAC,∴AO=DO.
由(1)知四边形ABCD是菱形,
∴AC=2AO,DB=2DO,∴AC=BD,
∴菱形ABCD是正方形.
随堂练习
5.如图,在四边形ABCD中,AB=BC
,对角线BD平分?ABC,P是BD上一点,过点P作PM?AD,PN?CD
,垂足分别为M、N.
(1)
求证:?ADB=?CDB;
(2)
若?ADC=90?,求证:四边形MPND是正方形.
C
A
B
D
P
M
N
证明:(1)∵AB
=
BC,BD平分∠ABC.
∴∠1=∠2.
∴△ABD≌△CBD
(AAS).
∴∠ADB=∠CDB.
1
2
随堂练习
C
A
B
D
P
M
N
(2)∵∠ADC=90°;
又∵PM⊥AD,PN⊥CD;
∴∠PMD=∠PND=90°.
∴四边形NPMD是矩形.
∵∠ADB=∠CDB;
∴∠ADB=∠CDB=45°.
∴∠MPD=∠NPD=45°.
∴DM=PM,DN=PN.
∴四边形NPMD是正方形(有一组邻边相等的矩形是正方形).
课堂小结
有一个角是90°
(或对角线互相垂直)
有一对邻边相等
(或对角线相等)
平行四边形
矩形
菱形
正方形
一组邻边相等且一个内角为直角
(或对角线互相垂直平分且相等)
有一个角是90°
(或对角线互相垂直)
有一对邻边相等
(或对角线相等)
1.3
正方形的性质与判定
学习目标
1.掌握正方形的判定方法;会运用正方形的判定条件进行有关的论证和计算.
2.理解特殊的平行四边形之间的内在联系,形成辨证看问题的观点.
什么是正方形?正方形有哪些性质?
正方形:有一组邻边相等,并且有一个角是直角的平行四边形.
正方形性质:①四个角都是直角;
②四条边都相等;
③对角线相等且互相垂直平分.
A
B
C
D
O
你是如何判断是矩形、菱形?
平行四边形
矩形
菱形
四边形
三个角是直角
四条边相等
定义
三个判定定理
定义
对角线相等
定义
对角线垂直
合作探究
想一想:将矩形纸片对折两次,怎样裁剪才能使剪下的三角形
展开后是个正方形?
(1)
(2)
(3)
(4)
合作探究
满足什么条件的矩形是正方形?满足什么条件的菱形是正方形?
矩形
正方形
一组邻边相等
对角线互相垂直
菱形
正方形
一个角是直角
对角线相等
新课讲授
正方形判定定理
1.对角线相等的菱形是正方形.
2.对角线垂直的矩形是正方形.
3.有一个角是直角的菱形是正方形.
例1、如图,已知点E,F,G,H分别在正方形ABCD的各边上,且AE=BF=CG=DH,AF,BG,CH,DE分别相交于点A′,B′,C′,D′.
求证:四边形A′B′C′D′是正方形.
证明:在正方形ABCD中,
∵在△ABF和△BCG中,AB=BC,∠ABC=∠BCD,BF=CG,
∴△ABF≌△BCG.
∴∠BAF=∠GBC.
∵∠BAF+∠AFB=90°,∴∠CBG+∠AFB=90°.
∴∠BB′F=90°.
∴∠A′B′C′=90°.
∴同理可得∠B′C′D′=∠C′D′A′=90°.∴四边形A′B′C′D′是矩形.
∵在△AB′B和△BC′C中,∠BAF=∠CBG,∠AB′B=∠BC′C,AB=BC,
∴△AB′B≌△BC′C.
∴AB′=BC′.
∵在△AA′E和△BB′F中,∠BAF=∠CBG,∠AA′E=∠BB′F,AE=BF,
∴△AA′E≌△BB′F,∴AA′=BB′.
∴A′B′=B′C′.
∴矩形A′B′C′D′是正方形.
例2、菱形EFGH的三个顶点E,G,H分别在正方形ABCD的边AB,CD,DA上,连接CF.
(1)求证:∠HEA=∠CGF;
(2)当AH=DG时,求证:菱形EFGH为正方形.
证明:(1)如图,连接GE,
∵AB∥CD,∴∠AEG=∠CGE.
∵GF∥HE,∴∠HEG=∠FGE.
∴∠HEA=∠CGF.
例2、菱形EFGH的三个顶点E,G,H分别在正方形ABCD的边AB,CD,DA上,连接CF.
(1)求证:∠HEA=∠CGF;
(2)当AH=DG时,求证:菱形EFGH为正方形.
(2)∵四边形ABCD是正方形,∴∠D=∠A=90°.
∵四边形EFGH是菱形,∴HG=HE.
在Rt△HAE和Rt△GDH中,AH=DG,HE=HG,
∴Rt△HAE≌Rt△GDH(HL).
∴∠AHE=∠DGH.
又∠DHG+∠DGH=90°,
∴∠DHG+∠AHE=90°.∴∠GHE=90°.
∴菱形EFGH为正方形.
合作探究
做一做:顺次连接任意四边形各边中点所得的四边形是平行四边形.顺次连接矩形、正方形各边中点能得到怎样的特殊平行四边形?
A
B
C
D
A
B
C
D
A
B
C
D
矩形
正方形
任意四边形
平行四边形
菱形
正方形
E
F
G
H
E
F
G
H
E
F
G
H
新课讲授
常见中点四边形比较
名称
任意四边形
矩形
菱形
正方形
对角线特点
既不垂直
也不相等
不垂直,仅相等
垂直但不相等
垂直且相等
中点四边形
基本图形
A
B
C
D
E
F
G
H
平行四边形
A
B
C
D
E
F
G
H
菱形
A
B
C
D
E
F
G
H
A
B
C
D
E
F
G
H
矩形
正方形
例3、如图,在矩形ABCD中,M、N分别是AD、BC的中点,E、F分别是边BM、CM的中点,当AB∶AD=________时,四边形MENF是正方形.
解:当AB∶AD=1∶2时,四边形MENF是正方形.
∵AB∶AD=1∶2,AM=DM,AB=CD,∴AB=AM=DM=DC,
∵∠A=∠D=90°,
∴∠ABM=∠AMB=∠DMC=∠DCM=45°,∴∠BMC=90°.
∵四边形ABCD是矩形,∴∠ABC=∠DCB=90°,
∴∠MBC=∠MCB=45°,∴BM=CM.
∵N、E、F分别是BC、BM、CM的中点,
∴BE=CF=ME=MF,NF∥BM,NE∥CM,
∴四边形MENF是平行四边形,
∵ME=MF,∠BMC=90°,
∴四边形MENF是正方形.
随堂练习
1.在四边形ABCD中,O是对角线的交点,能判定这个四边形是正方形的条件是?( )
A.AC=BD,AB//CD
B.AD∥BC,∠A=∠C
C.AO=BO=CO=DO,
AC⊥BD
D.AO=CO,BO=DO,
AB=BC
C
A
B
C
D
O
随堂练习
2.如图所示,在四边形ABCD中,AB=BC=CD=DA,对角线AC与BD相交于点O.若不添加任何字母与辅助线,要使得四边形ABCD是正方形,则还需添加的一个条件是___________________.
AC=BD(答案不唯一)
A
B
C
D
O
随堂练习
3.将五个边长都为2
cm的正方形按如图所示摆放,点A、B、C、D分别是四个正方形的中心,则图中四块阴影面积的和为?( )
A.2
cm2 ????B.4
cm2 ????C.6
cm2 ????D.8
cm2
B
随堂练习
4.如图所示,在ABCD中,对角线AC,BD交于点O,E是BD延长线上的点,且EA=EC.
(1)求证:四边形ABCD是菱形;
(2)若∠DAC=∠EAD+∠AED,求证:四边形ABCD是正方形.
证明:(1)∵四边形ABCD是平行四边形,
∴AO=CO=AC,
∵EA=EC,
∴EO⊥AC,即BD⊥AC,
∴平行四边形ABCD是菱形.
随堂练习
4.如图所示,在ABCD中,对角线AC,BD交于点O,E是BD延长线上的点,且EA=EC.
(1)求证:四边形ABCD是菱形;
(2)若∠DAC=∠EAD+∠AED,求证:四边形ABCD是正方形.
(2)∵∠1=∠EAD+∠AED,
∠DAC=∠EAD+∠AED,
∴∠1=∠DAC,∴AO=DO.
由(1)知四边形ABCD是菱形,
∴AC=2AO,DB=2DO,∴AC=BD,
∴菱形ABCD是正方形.
随堂练习
5.如图,在四边形ABCD中,AB=BC
,对角线BD平分?ABC,P是BD上一点,过点P作PM?AD,PN?CD
,垂足分别为M、N.
(1)
求证:?ADB=?CDB;
(2)
若?ADC=90?,求证:四边形MPND是正方形.
C
A
B
D
P
M
N
证明:(1)∵AB
=
BC,BD平分∠ABC.
∴∠1=∠2.
∴△ABD≌△CBD
(AAS).
∴∠ADB=∠CDB.
1
2
随堂练习
C
A
B
D
P
M
N
(2)∵∠ADC=90°;
又∵PM⊥AD,PN⊥CD;
∴∠PMD=∠PND=90°.
∴四边形NPMD是矩形.
∵∠ADB=∠CDB;
∴∠ADB=∠CDB=45°.
∴∠MPD=∠NPD=45°.
∴DM=PM,DN=PN.
∴四边形NPMD是正方形(有一组邻边相等的矩形是正方形).
课堂小结
有一个角是90°
(或对角线互相垂直)
有一对邻边相等
(或对角线相等)
平行四边形
矩形
菱形
正方形
一组邻边相等且一个内角为直角
(或对角线互相垂直平分且相等)
有一个角是90°
(或对角线互相垂直)
有一对邻边相等
(或对角线相等)
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
