2021年苏科新版八年级上册《第1章 全等三角形》单元测试卷(word解析版)
文档属性
| 名称 | 2021年苏科新版八年级上册《第1章 全等三角形》单元测试卷(word解析版) |
|
|
| 格式 | zip | ||
| 文件大小 | 226.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-18 00:00:00 | ||
图片预览

文档简介
苏科新版八年级上册《第1章
全等三角形》2021年单元测试卷一.选择题(共7小题,满分21分,每小题3分)
1.如图,两个三角形是全等三角形,那么x的值是( )
A.30°
B.45°
C.50°
D.85°
2.如图,△ABC≌△DEF,BC=7,EC=4,则CF的长为( )
A.2
B.3
C.5
D.7
3.根据下列已知条件,能作出唯一△ABC的是( )
A.AB=3,BC=4,CA=8
B.AB=4,BC=3,∠A=60°
C.∠A=60°,∠B=45°,AB=4
D.∠C=90°,∠B=30°,∠A=60°
4.如图,已知∠ABC=∠DCB,下列所给条件不能证明△ABC≌△DCB的是( )
A.∠A=∠D
B.AB=DC
C.∠ACB=∠DBC
D.AC=BD
5.下列条件不可以判定两个直角三角形全等的是( )
A.两条直角边对应相等
B.有两条边对应相等
C.一条边和一锐角对应相等
D.一条边和一个角对应相等
6.如图,小华书上的三角形被墨水弄污了一部分,他能在作业本上作一个完全一样的三角形,其根据为( )
A.SSS
B.SAS
C.ASA
D.AAS
7.如图,D为△ABC边BC上一点,AB=AC,∠BAC=56°,且BF=DC,EC=BD,则∠EDF等于( )
A.62°
B.56°
C.34°
D.124°
二.填空题(共8小题,满分24分,每小题3分)
8.一个三角形的三边为2、5、x,另一个三角形的三边为y、2、6,若这两个三角形全等,则x+y=
.
9.如图,小明与小红玩跷跷板游戏,如果跷跷板的支点O(即跷跷板的中点)至地面的距离是50cm,当小红从水平位置CD下降40cm时,这时小明离地面的高度是
cm.
10.如图是由4个相同的小正方形组成的网格图,其中∠1+∠2等于
.
11.如图,∠BAC=∠ABD,请你添加一个条件:
,使AC=BD(只添一个即可).
12.如图所示,△BKC≌△BKE≌△DKC,BE与KD交于点G,KE与CD交于点P,BE与CD交于点A,∠BKC=134°,∠E=22°,则∠KPD=
.
13.如图,已知AB=AC,D为∠BAC的角平分线上面一点,连接BD,CD;如图2,已知AB=AC,D、E为∠BAC的角平分线上面两点,连接BD,CD,BE,CE;如图3,已知AB=AC,D、E、F为∠BAC的角平分线上面三点,连接BD,CD,BE,CE,BF,CF;…,依次规律,第n个图形中有全等三角形的对数是
.
14.起重机的吊臂都是用铁条焊成三角形,这是利用了
.
15.如图,在△ABC和△BAD中,BC=AD,请你再补充一个条件,使△ABC≌△BAD.你补充的条件是
(只填一个).
三.解答题(共8小题,满分75分)
16.如图,把两根钢条AA′,BB′的中点O连在一起,可以做成一个测量工件内槽宽的工具(工人把这种工具叫卡钳)只要量出A′B′的长度,就可以知道工件的内径AB是否符合标准,你能简要说出工人这样测量的道理吗?
17.如图,∠A=∠D=90°,AB=DE,BF=EC.求证:Rt△ABC≌Rt△DEF.
18.如图,线段AD、BE相交于点C,且△ABC≌△DEC,点M、N分别为线段AC、CD的中点.
求证:(1)ME=BN;
(2)ME∥BN.
19.如图,已知△ABC中,AB=AC,AD平分∠BAC,请补充完整过程说明△ABD≌△ACD的理由.
20.如图,等腰直角三角形ABC中,∠C=90°,∠A的平分线AD交BC于点D,过B作BE⊥AD,垂足为E,求证:AD=2BE.
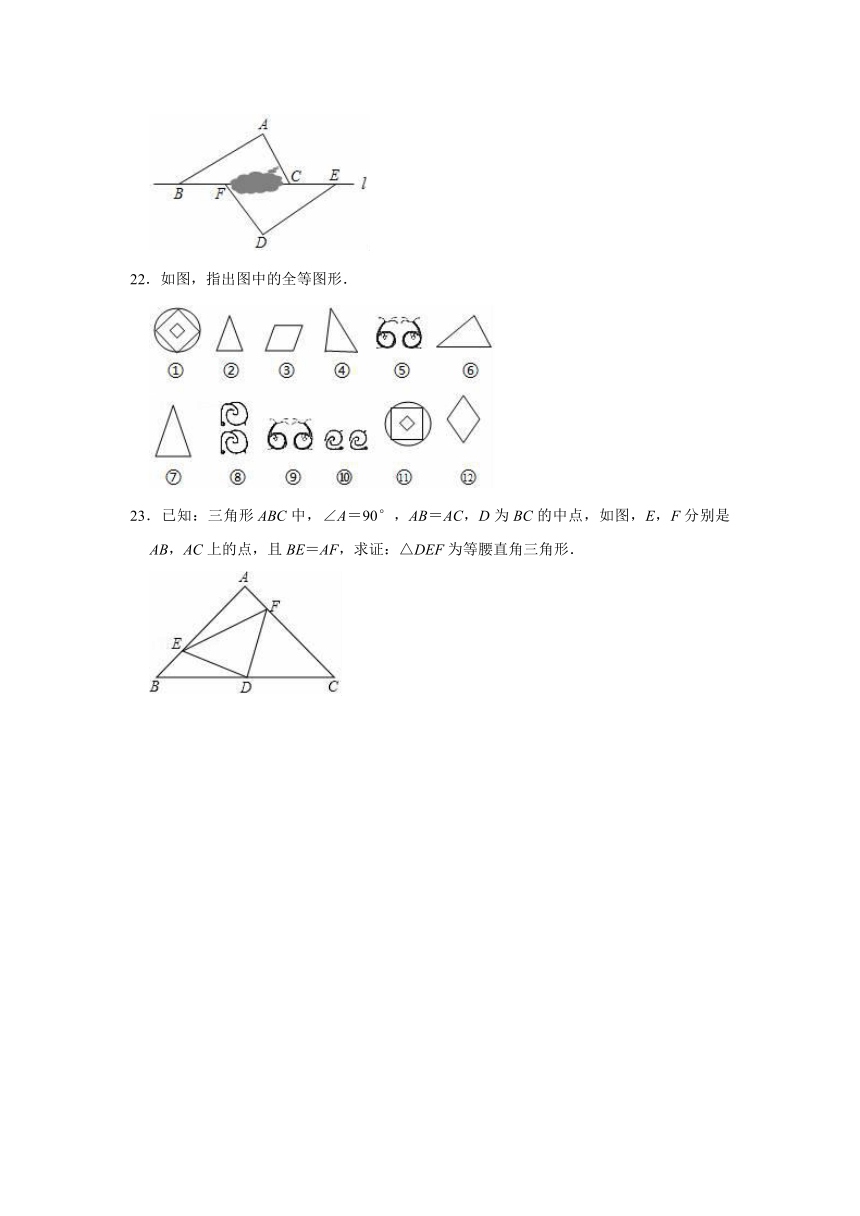
21.如图,点B、F、C、E在直线l上(F、C之间不能直接测量),点A、D在l异侧,测得AB=DE,AB∥DE,∠A=∠D.
(1)求证:△ABC≌△DEF;
(2)若BE=10m,BF=3m,求FC的长度.
22.如图,指出图中的全等图形.
23.已知:三角形ABC中,∠A=90°,AB=AC,D为BC的中点,如图,E,F分别是AB,AC上的点,且BE=AF,求证:△DEF为等腰直角三角形.
参考答案与试题解析
一.选择题(共7小题,满分21分,每小题3分)
1.解:180°﹣85°﹣45°=50°,
∵两个三角形是全等三角形,
∴x=50°,
故选:C.
2.解:∵△ABC≌△DEF,
∴EF=BC=7,
∵EC=4,
∴CF=3,
故选:B.
3.解:A.∵AB=3,BC=4,CA=8,AB+BC<CA,
∴不能画出三角形,故本选项不合题意;
B.AB=4,BC=3,∠A=60°,不能画出唯一三角形,故本选项不合题意;
C.当∠A=60°,∠B=45°,AB=4时,根据“ASA”可判断△ABC的唯一性;
D.已知三个角,不能画出唯一三角形,故本选项不符合题意;
故选:C.
4.解:A、添加∠A=∠D可利用AAS判定△ABC≌△DCB,故此选项不合题意;
B、添加AB=DC可利用SAS定理判定△ABC≌△DCB,故此选项不合题意;
C、添加∠ACB=∠DBC可利用ASA定理判定△ABC≌△DCB,故此选项不合题意;
D、添加AC=BD不能判定△ABC≌△DCB,故此选项符合题意;
故选:D.
5.解:∵A、两条直角边对应相等
可利用SAS判定两直角三角形全等,
B、两边对应相等,可利用HL或SSA判定两直角三角形全等;
C、一条边和一锐角对应相等,可利用AAS或ASA判定两直角三角形全等.
D、一条边和一个角对应相等不能判定两直角三角形全等.
故选:D.
6.解:根据图示,得:该三角形的两角及其夹边确定.
∴根据全等三角形的判定,由ASA可作出一个完全一样的三角形.
故选:C.
7.解:∵AB=AC,
∴∠B=∠C=(180°﹣∠BAC)=(180°﹣56°)=62°,
在△BFD和△EDC中,,
∴△BFD≌△EDC(SAS),
∴∠BFD=∠EDC,
∴∠FDB+∠EDC=∠FDB+∠BFD=180°﹣∠B=180°﹣62°=118°,
则∠EDF=180°﹣(∠FDB+∠EDC)=180°﹣118°=62°.
故选:A.
二.填空题(共8小题,满分24分,每小题3分)
8.解:∵这两个三角形全等,两个三角形中都有2
∴长度为2的是对应边,x应是另一个三角形中的边6.同理可得y=5
∴x+y=11.
故答案为:11.
9.解:在△OCF与△ODG中,,
∴△OCF≌△ODG(AAS),
∴CF=DG=40,
∴小明离地面的高度是50+40=90,
故答案为:90.
10.解:由题意得:AB=DB,AC=ED,∠A=∠D=90°,
∵在△ABC和△DBE中,
∴△ABC≌△DBE(SAS),
∴∠1=∠ACB,
∵∠ACB+∠2=180°,
∴∠1+∠2=180°,
故答案为:180°.
11.解:∠BAC=∠ABD(已知),∠D=∠C,AB=BA(公共边),
∴△DAB≌△CBA(AAS);
∴AC=BD,
故答案为:∠D=∠C.本题答案不唯一.
12.解:∵△BKC≌△BKE,∠BKC=134°,
∴∠BKE=∠BKC=134°,
∴∠PKC=360°﹣134°﹣134°=92°,
∵△BKE≌△DKC,∠E=22°,
∴∠DCK=∠E=22°,
∴∠KPD=∠PKC+∠DCK=92°+22°=114°,
故答案为:114°.
13.解:当有1点D时,有1对全等三角形;
当有2点D、E时,有3对全等三角形;
当有3点D、E、F时,有6对全等三角形;
当有4点时,有10个全等三角形;
…
当有n个点时,图中有个全等三角形.
故答案为:.
14.解:起重机的臂膀中都有三角形结构,这是利用了三角形的稳定性.
故答案为:三角形的稳定性.
15.解:欲证两三角形全等,已有条件:BC=AD,AB=AB,
所以补充两边夹角∠CBA=∠DAB便可以根据SAS证明;
补充AC=BD便可以根据SSS证明.
故补充的条件是AC=BD(或∠CBA=∠DAB).
故答案是:AC=BD(或∠CBA=∠DAB).
三.解答题(共8小题,满分75分)
16.解:此工具是根据三角形全等制作而成的.
∵O是AA′,BB′的中点,
∴AO=A′O,BO=B′O,
又∵∠AOB与∠A′OB′是对顶角,
∴∠AOB=∠A′OB′,
在△AOB和△A′OB′中,
∵,
∴△AOB≌△A′OB′(SAS),
∴A′B′=AB,
∴只要量出A′B′的长度,就可以知道工作的内径AB是否符合标准.
17.证明:∵BF=EC,
∴BF+FC=FC+EC,即BC=EF,
∵∠A=∠D=90°,
∴△ABC和△DEF都是直角三角形,
在Rt△ABC和Rt△DEF中
,
∴Rt△ABC≌Rt△DEF(HL).
18.证明:(1)连接BM、EN,
∵△ABC≌△DEC,
∴AC=DC,BC=EC,
∵点M、N分别为线段AC、CD的中点,
∴CM=CN,
∴四边形MBNE是平行四边形,
∴ME=BN;
(2)∵四边形MBNE是平行四边形,
∴ME∥BN.
19.证明:∵AD平分∠BAC,
∴∠BAD=∠CAD
(
角平分线的定义
)
在△ABD和△ACD中
∴△ABD≌△ACD(
SAS).
20.证明:延长BE和AC后相交于点M,
如图所示:
∵△ABC是等腰直角三角形,
∴AC=BC,
又∵AD是∠A的平分线,
∠MAE=∠BAE,
又∵BE⊥AD,
∴∠AEB=∠AEM=90°,
在△AME和△BAE中
∴△AME≌△BAE(ASA)
∴BE=ME,
∴BM=2BE,
又∵∠ACB=90°,
∴∠ADC+∠DAC=90°,
又∵∠BDE+∠DBE=90°,
∠ADC=∠BDE,
∴∠DAC=∠MBC,
在△ACD和△BCM中,
∴△ACD≌△BCM(ASA)
∴AD=BM
∴AD=2BE.
21.(1)证明:∵AB∥DE,
∴∠ABC=∠DEF,
在△ABC与△DEF中
∴△ABC≌△DEF;
(2)∵△ABC≌△DEF,
∴BC=EF,
∴BF+FC=EC+FC,
∴BF=EC,
∵BE=10m,BF=3m,
∴FC=10﹣3﹣3=4m.
22.解:⑤和⑨是全等形;
故答案为:⑤和⑨.
23.证明:连接AD,
∵AB=AC,∠BAC=90°,D为BC中点,
∴AD==BD=CD,
且AD平分∠BAC,
∴∠BAD=∠CAD=45°,
在△BDE和△ADF中,
∴△BDE≌△ADF,
∴DE=DF,∠BDE=∠ADF,
∵∠BDE+∠ADE=90°,
∴∠ADF+∠ADE=90°,
即:∠EDF=90°,
∴△DEF为等腰直角三角形.
全等三角形》2021年单元测试卷一.选择题(共7小题,满分21分,每小题3分)
1.如图,两个三角形是全等三角形,那么x的值是( )
A.30°
B.45°
C.50°
D.85°
2.如图,△ABC≌△DEF,BC=7,EC=4,则CF的长为( )
A.2
B.3
C.5
D.7
3.根据下列已知条件,能作出唯一△ABC的是( )
A.AB=3,BC=4,CA=8
B.AB=4,BC=3,∠A=60°
C.∠A=60°,∠B=45°,AB=4
D.∠C=90°,∠B=30°,∠A=60°
4.如图,已知∠ABC=∠DCB,下列所给条件不能证明△ABC≌△DCB的是( )
A.∠A=∠D
B.AB=DC
C.∠ACB=∠DBC
D.AC=BD
5.下列条件不可以判定两个直角三角形全等的是( )
A.两条直角边对应相等
B.有两条边对应相等
C.一条边和一锐角对应相等
D.一条边和一个角对应相等
6.如图,小华书上的三角形被墨水弄污了一部分,他能在作业本上作一个完全一样的三角形,其根据为( )
A.SSS
B.SAS
C.ASA
D.AAS
7.如图,D为△ABC边BC上一点,AB=AC,∠BAC=56°,且BF=DC,EC=BD,则∠EDF等于( )
A.62°
B.56°
C.34°
D.124°
二.填空题(共8小题,满分24分,每小题3分)
8.一个三角形的三边为2、5、x,另一个三角形的三边为y、2、6,若这两个三角形全等,则x+y=
.
9.如图,小明与小红玩跷跷板游戏,如果跷跷板的支点O(即跷跷板的中点)至地面的距离是50cm,当小红从水平位置CD下降40cm时,这时小明离地面的高度是
cm.
10.如图是由4个相同的小正方形组成的网格图,其中∠1+∠2等于
.
11.如图,∠BAC=∠ABD,请你添加一个条件:
,使AC=BD(只添一个即可).
12.如图所示,△BKC≌△BKE≌△DKC,BE与KD交于点G,KE与CD交于点P,BE与CD交于点A,∠BKC=134°,∠E=22°,则∠KPD=
.
13.如图,已知AB=AC,D为∠BAC的角平分线上面一点,连接BD,CD;如图2,已知AB=AC,D、E为∠BAC的角平分线上面两点,连接BD,CD,BE,CE;如图3,已知AB=AC,D、E、F为∠BAC的角平分线上面三点,连接BD,CD,BE,CE,BF,CF;…,依次规律,第n个图形中有全等三角形的对数是
.
14.起重机的吊臂都是用铁条焊成三角形,这是利用了
.
15.如图,在△ABC和△BAD中,BC=AD,请你再补充一个条件,使△ABC≌△BAD.你补充的条件是
(只填一个).
三.解答题(共8小题,满分75分)
16.如图,把两根钢条AA′,BB′的中点O连在一起,可以做成一个测量工件内槽宽的工具(工人把这种工具叫卡钳)只要量出A′B′的长度,就可以知道工件的内径AB是否符合标准,你能简要说出工人这样测量的道理吗?
17.如图,∠A=∠D=90°,AB=DE,BF=EC.求证:Rt△ABC≌Rt△DEF.
18.如图,线段AD、BE相交于点C,且△ABC≌△DEC,点M、N分别为线段AC、CD的中点.
求证:(1)ME=BN;
(2)ME∥BN.
19.如图,已知△ABC中,AB=AC,AD平分∠BAC,请补充完整过程说明△ABD≌△ACD的理由.
20.如图,等腰直角三角形ABC中,∠C=90°,∠A的平分线AD交BC于点D,过B作BE⊥AD,垂足为E,求证:AD=2BE.
21.如图,点B、F、C、E在直线l上(F、C之间不能直接测量),点A、D在l异侧,测得AB=DE,AB∥DE,∠A=∠D.
(1)求证:△ABC≌△DEF;
(2)若BE=10m,BF=3m,求FC的长度.
22.如图,指出图中的全等图形.
23.已知:三角形ABC中,∠A=90°,AB=AC,D为BC的中点,如图,E,F分别是AB,AC上的点,且BE=AF,求证:△DEF为等腰直角三角形.
参考答案与试题解析
一.选择题(共7小题,满分21分,每小题3分)
1.解:180°﹣85°﹣45°=50°,
∵两个三角形是全等三角形,
∴x=50°,
故选:C.
2.解:∵△ABC≌△DEF,
∴EF=BC=7,
∵EC=4,
∴CF=3,
故选:B.
3.解:A.∵AB=3,BC=4,CA=8,AB+BC<CA,
∴不能画出三角形,故本选项不合题意;
B.AB=4,BC=3,∠A=60°,不能画出唯一三角形,故本选项不合题意;
C.当∠A=60°,∠B=45°,AB=4时,根据“ASA”可判断△ABC的唯一性;
D.已知三个角,不能画出唯一三角形,故本选项不符合题意;
故选:C.
4.解:A、添加∠A=∠D可利用AAS判定△ABC≌△DCB,故此选项不合题意;
B、添加AB=DC可利用SAS定理判定△ABC≌△DCB,故此选项不合题意;
C、添加∠ACB=∠DBC可利用ASA定理判定△ABC≌△DCB,故此选项不合题意;
D、添加AC=BD不能判定△ABC≌△DCB,故此选项符合题意;
故选:D.
5.解:∵A、两条直角边对应相等
可利用SAS判定两直角三角形全等,
B、两边对应相等,可利用HL或SSA判定两直角三角形全等;
C、一条边和一锐角对应相等,可利用AAS或ASA判定两直角三角形全等.
D、一条边和一个角对应相等不能判定两直角三角形全等.
故选:D.
6.解:根据图示,得:该三角形的两角及其夹边确定.
∴根据全等三角形的判定,由ASA可作出一个完全一样的三角形.
故选:C.
7.解:∵AB=AC,
∴∠B=∠C=(180°﹣∠BAC)=(180°﹣56°)=62°,
在△BFD和△EDC中,,
∴△BFD≌△EDC(SAS),
∴∠BFD=∠EDC,
∴∠FDB+∠EDC=∠FDB+∠BFD=180°﹣∠B=180°﹣62°=118°,
则∠EDF=180°﹣(∠FDB+∠EDC)=180°﹣118°=62°.
故选:A.
二.填空题(共8小题,满分24分,每小题3分)
8.解:∵这两个三角形全等,两个三角形中都有2
∴长度为2的是对应边,x应是另一个三角形中的边6.同理可得y=5
∴x+y=11.
故答案为:11.
9.解:在△OCF与△ODG中,,
∴△OCF≌△ODG(AAS),
∴CF=DG=40,
∴小明离地面的高度是50+40=90,
故答案为:90.
10.解:由题意得:AB=DB,AC=ED,∠A=∠D=90°,
∵在△ABC和△DBE中,
∴△ABC≌△DBE(SAS),
∴∠1=∠ACB,
∵∠ACB+∠2=180°,
∴∠1+∠2=180°,
故答案为:180°.
11.解:∠BAC=∠ABD(已知),∠D=∠C,AB=BA(公共边),
∴△DAB≌△CBA(AAS);
∴AC=BD,
故答案为:∠D=∠C.本题答案不唯一.
12.解:∵△BKC≌△BKE,∠BKC=134°,
∴∠BKE=∠BKC=134°,
∴∠PKC=360°﹣134°﹣134°=92°,
∵△BKE≌△DKC,∠E=22°,
∴∠DCK=∠E=22°,
∴∠KPD=∠PKC+∠DCK=92°+22°=114°,
故答案为:114°.
13.解:当有1点D时,有1对全等三角形;
当有2点D、E时,有3对全等三角形;
当有3点D、E、F时,有6对全等三角形;
当有4点时,有10个全等三角形;
…
当有n个点时,图中有个全等三角形.
故答案为:.
14.解:起重机的臂膀中都有三角形结构,这是利用了三角形的稳定性.
故答案为:三角形的稳定性.
15.解:欲证两三角形全等,已有条件:BC=AD,AB=AB,
所以补充两边夹角∠CBA=∠DAB便可以根据SAS证明;
补充AC=BD便可以根据SSS证明.
故补充的条件是AC=BD(或∠CBA=∠DAB).
故答案是:AC=BD(或∠CBA=∠DAB).
三.解答题(共8小题,满分75分)
16.解:此工具是根据三角形全等制作而成的.
∵O是AA′,BB′的中点,
∴AO=A′O,BO=B′O,
又∵∠AOB与∠A′OB′是对顶角,
∴∠AOB=∠A′OB′,
在△AOB和△A′OB′中,
∵,
∴△AOB≌△A′OB′(SAS),
∴A′B′=AB,
∴只要量出A′B′的长度,就可以知道工作的内径AB是否符合标准.
17.证明:∵BF=EC,
∴BF+FC=FC+EC,即BC=EF,
∵∠A=∠D=90°,
∴△ABC和△DEF都是直角三角形,
在Rt△ABC和Rt△DEF中
,
∴Rt△ABC≌Rt△DEF(HL).
18.证明:(1)连接BM、EN,
∵△ABC≌△DEC,
∴AC=DC,BC=EC,
∵点M、N分别为线段AC、CD的中点,
∴CM=CN,
∴四边形MBNE是平行四边形,
∴ME=BN;
(2)∵四边形MBNE是平行四边形,
∴ME∥BN.
19.证明:∵AD平分∠BAC,
∴∠BAD=∠CAD
(
角平分线的定义
)
在△ABD和△ACD中
∴△ABD≌△ACD(
SAS).
20.证明:延长BE和AC后相交于点M,
如图所示:
∵△ABC是等腰直角三角形,
∴AC=BC,
又∵AD是∠A的平分线,
∠MAE=∠BAE,
又∵BE⊥AD,
∴∠AEB=∠AEM=90°,
在△AME和△BAE中
∴△AME≌△BAE(ASA)
∴BE=ME,
∴BM=2BE,
又∵∠ACB=90°,
∴∠ADC+∠DAC=90°,
又∵∠BDE+∠DBE=90°,
∠ADC=∠BDE,
∴∠DAC=∠MBC,
在△ACD和△BCM中,
∴△ACD≌△BCM(ASA)
∴AD=BM
∴AD=2BE.
21.(1)证明:∵AB∥DE,
∴∠ABC=∠DEF,
在△ABC与△DEF中
∴△ABC≌△DEF;
(2)∵△ABC≌△DEF,
∴BC=EF,
∴BF+FC=EC+FC,
∴BF=EC,
∵BE=10m,BF=3m,
∴FC=10﹣3﹣3=4m.
22.解:⑤和⑨是全等形;
故答案为:⑤和⑨.
23.证明:连接AD,
∵AB=AC,∠BAC=90°,D为BC中点,
∴AD==BD=CD,
且AD平分∠BAC,
∴∠BAD=∠CAD=45°,
在△BDE和△ADF中,
∴△BDE≌△ADF,
∴DE=DF,∠BDE=∠ADF,
∵∠BDE+∠ADE=90°,
∴∠ADF+∠ADE=90°,
即:∠EDF=90°,
∴△DEF为等腰直角三角形.
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
