第二讲 一定是直角三角形吗(考点讲解)(含答案)
文档属性
| 名称 | 第二讲 一定是直角三角形吗(考点讲解)(含答案) | 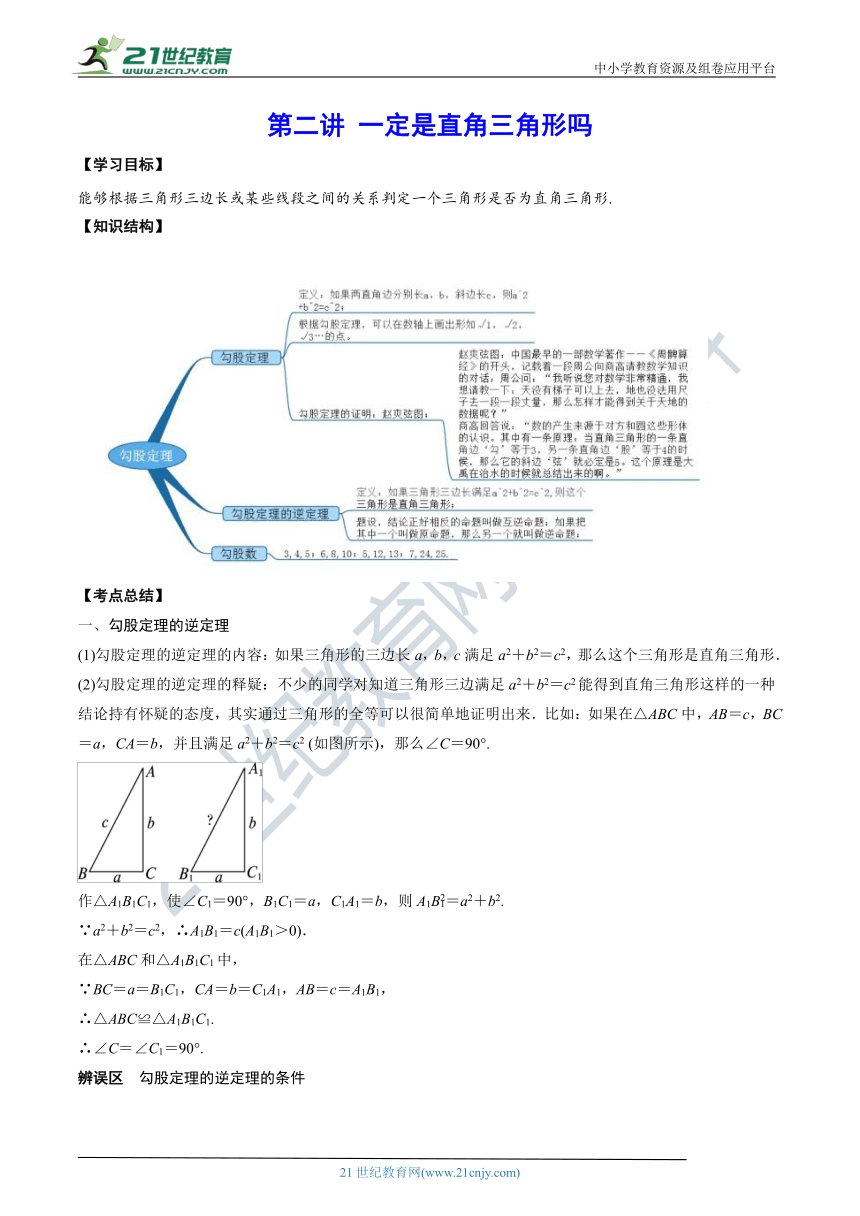 | |
| 格式 | doc | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-19 10:22:52 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
第二讲
一定是直角三角形吗
【学习目标】
能够根据三角形三边长或某些线段之间的关系判定一个三角形是否为直角三角形.
【知识结构】
(?http:?/??/?www.21cnjy.com?/??)
【考点总结】
一、勾股定理的逆定理
(1)勾股定理的逆定理的内容:如果三角形的三边长a,b,c满足a2+b2=c2,那么这个三角形是直角三角形.
(2)勾股定理的逆定理的释疑:不少
(?http:?/??/?www.21cnjy.com?)的同学对知道三角形三边满足a2+b2=c2能得到直角三角形这样的一种结论持有怀疑的态度,其实通过三角形的全等可以很简单地证明出来.比如:如果在△ABC中,AB=c,BC=a,CA=b,并且满足a2+b2=c2
(如图所示),那么∠C=90°.2·1·c·n·j·y
(?http:?/??/?www.21cnjy.com?/??)
作△A1B1C1,使∠C1=90°,B1C1=a,C1A1=b,则A1B=a2+b2.
∵a2+b2=c2,∴A1B1=c(A1B1>0).
在△ABC和△A1B1C1中,
∵BC=a=B1C1,CA=b=C1A1,AB=c=A1B1,
∴△ABC≌△A1B1C1.
∴∠C=∠C1=90°.
辨误区
勾股定理的逆定理的条件
(1)不能说成在直角三角形中,因为还没有确定直角三角形,当然也不能说“斜边”和“直角边”.
(2)当满足a2+b2=c2时,c是斜边,∠C是直角.
利用勾股定理的逆定理判断一个三角形是否为
(?http:?/??/?www.21cnjy.com?)直角三角形的思路是:先确定最长边,算出最长边的平方及另两边的平方和,如果最长边的平方与另两边的平方和相等,则此三角形为直角三角形.
对啊!到目前为止判定直角三角形的方法有:
①说明三角形中有一个直角;
②说明三角形中有两边互相垂直;
③勾股定理的逆定理.
二、勾股定理的逆定理与勾股定理的关系
勾股定理是通过“形”的状态来反映“数”的关系的,而勾股定理的逆定理是通过“数”的关系来反映“形”的状态的.21cnjy.com
(1)勾股定理是直角三角形的性质定理,勾股定理的逆定理是直角三角形的判定定理,二者是互逆的.
(2)联系:①两者都与a2+b2=c2有关,②两者所讨论的问题都是直角三角形问题.
(3)区别:勾股定理是以“
(?http:?/??/?www.21cnjy.com?)一个三角形是直角三角形”为条件,进而得到这个直角三角形三边的数量关系“a2+b2=c2”;勾股定理的逆定理则是以“一个三角形的三边满足a2+b2=c2”为条件,进而得到这个三角形是“直角三角形”.www-2-1-cnjy-com
(4)二者关系可列表如下:
定理
勾股定理
勾股定理的逆定理
内容
如果直角三角形的两直角边长分别为a,b,斜边长为c,那么a2+b2=c2
如果三角形的三边长a,b,c满足a2+b2=c2,那么这个三角形是直角三角形
题设
直角三角形的两直角边长分别为a,b,斜边长为c
三角形的三边长a,b,c满足a2+b2=c2
结论
a2+b2=c2
三角形是直角三角形
用途
是直角三角形的一个性质
判定直角三角形的一种方法
三、勾股数
勾股数:满足a2+b2=c2的三个正整数,称为勾股数.
(1)由定义可知,一组数是勾股数必须满足两个条件:①满足a2+b2=c2;②都是正整数.两者缺一不可.
(2)将一组勾股数同时扩大或缩
(?http:?/??/?www.21cnjy.com?)小相同的倍数所得的数仍满足a2+b2=c2(但不一定是勾股数),以它们为边长的三角形是直角三角形,比如以0.3
cm,0.4
cm,0.5
cm为边长的三角形是直角三角形.
四、勾股定理的逆定理的应用
勾股定理的逆定理在解决实
(?http:?/??/?www.21cnjy.com?)际问题中有着广泛的应用,可以用它来判定是不是直角.家里建房时,常需要在现场画出直角,在没有测量角的仪器的情况下,工人师傅常常利用勾股定理的逆定理作出直角.
五、利用非负数的性质判定三角形的形状
在由一个等式求三角形的三边长时,往往先把等式
(?http:?/??/?www.21cnjy.com?)化为a2+b2+c2=0的形式,再由a=0,b=0,c=0,求得三角形三边之长,利用计算来判断△ABC是否是直角三角形.【来源:21·世纪·教育·网】
谈重点
判定三角形的形状
由条件等式来判断三角形的形状,就是将已知的条件等式变形,再根据它的结构特点,得出a,b,c的关系,从而判断三角形的形状.2-1-c-n-j-y
六、勾股定理及其逆定理的综合应用
(1)利用勾股定理解决生活中的实际问题时,关键是利用转化的思想把实际问题转化为数学模型(直角三角形)来解决.21
cnjy
com
(2)综合运用勾股定理及其逆定理
(?http:?/??/?www.21cnjy.com?),将不规则图形转化为规则图形是常用的数学方法,在这里,一方面要熟记常用的勾股数;另一方面要注意到:如果一个三角形的三边长已知或具有某些比例关系,那么就可以用勾股定理的逆定理去验证其是否是直角三角形.
【来源:21cnj
y.co
m】
【例题讲解】
【类型】一、原命题与逆命题
例1、写出下列原命题的逆命题并判断是否正确
1.原命题:猫有四只脚.
2.原命题:对顶角相等.
3.原命题:线段垂直平分线上的点,到这条线段两端点的距离相等.
4.原命题:角平分线上的点,到这个角的两边距离相等.
【答案与解析】
1.
逆命题:有四只脚的是猫(不正确)
2.
逆命题:相等的角是对顶角(不正确)
3.
逆命题:到线段两端距离相等的点,在这条线段的垂直平分线上.(正确)
4.
逆命题:到角两边距离相等的点,在这个角的角平分线上.(正确)
【总结】掌握原命题与逆命题的关系.
原命题正确,逆命题未必正确;原命题不正确,其逆命题也不一定错误.www.21-cn-jy.com
【训练】下列命题中,其逆命题成立的是______________.(只填写序号)
①同旁内角互补,两直线平行;
②如果两个角是直角,那么它们相等;
③如果两个实数相等,那么它们的平方相等;
④如果三角形的三边长满足,那么这个三角形是直角三角形.
【答案】①④
提示:①的逆命题“两直线平行,同旁内角互补”显然正确;②的逆命题“如果两个角相等,那么它们是直角”很明显是错误的;③的逆命题“如果两个实数的平方相等,那么这两个实数相等”,两个实数可以互为相反数,所以该命题不正确;④的逆命题“如果三角形是直角三角形,那么三角形的三边长满足”也是正确的.【出处:21教育名师】
【类型】二、勾股定理的逆定理
例2、判断由线段组成的三角形是不是直角三角形.
(1)=7,=24,=25;
(2)=,=1,=;
(3),,();
【知识点提示】判断三条线段能否组成直角
(?http:?/??/?www.21cnjy.com?)三角形,关键是运用勾股定理的逆定理:看较短的两条线段的平方和是否等于最长线段的平方.若是,则为直角三角形,反之,则不是直角三角形.
【答案与解析】
解:(1)∵
,,
∴
.
∴
由线段组成的三角形是直角三角形.
(2)∵
,,,
∴
.
∴
由线段组成的三角形不是直角三角形.
(3)∵
,
∴
,.
∵,
,
∴
.
∴
由线段组成的三角形是直角三角形.
【提示】解此类题的关键是准确地判断哪一条边最大,然后再利用勾股定理的逆定理进行判断,即首先确定最大边,然后验证与是否具有相等关系,再根据结果判断是否为直角三角形.
【训练】判断以线段为边的△ABC是不是直角三角形,其中,,.
解:由于,因此为最大边,只需看是否等于即可.
∵
,,,∴
,
∴
以线段为边能构成以为斜边的直角三角形.
【训练】下列四组数:①5,12,
(?http:?/??/?www.21cnjy.com?)13;②7,24,25;③1,2,4;④5,6,8.其中可以为直角三角形三边长的有
.(把所有你认为正确的序号都写上)21教育网
【答案】①②;
解:①∵52+122=132,能构成直角三角形;
②72+242=252,能构成直角三角形;
③12+22≠42,不能构成直角三角形;
④52+62≠82,不能构成直角三角形.
所以①②.
故答案为:①②.
例3、
已知:如图,四边形ABCD中,AB⊥BC,AB=1,BC=2,CD=2,AD=3,求四边形ABCD的面积.
(?http:?/??/?www.21cnjy.com?/??)
解:连接AC.
∵∠ABC=90°,AB=1,BC=2,
∴AC==,
在△ACD中,AC2+CD2=5+4=9=AD2,
∴△ACD是直角三角形,
∴S四边形ABCD=AB?BC+AC?CD,
=×1×2+××2,
=1+.
故四边形ABCD的面积为1+.
(?http:?/??/?www.21cnjy.com?/??)
【提示】本题考查的是勾股定理的逆定理及三角形的面积,能根据勾股定理的逆定理判断出△ACD的形状是解答此题的关键.21·cn·jy·com
【训练】如图所示,在梯形ABCD中
(?http:?/??/?www.21cnjy.com?),AB∥CD,∠A=90°,AB=2,BC=3,CD=1,E是AD中点,试判断EC与EB的位置关系,并写出推理过程.21·世纪
教育网
(?http:?/??/?www.21cnjy.com?/??)
解:EC⊥EB.
过点C作CF⊥AB于F,则四边形AFCD是矩形,
在Rt△BCF中,可得CF=.
(?http:?/??/?www.21cnjy.com?/??)
则AD=CF=,故DE=AE=AD=.
在Rt△ABE和Rt△DCE中,
,.
∴
.
∵
BC=3,∴
.
∴
∠CEB=90°,∴
EB⊥EC.
【类型】三、勾股定理逆定理的实际应用
例4、“远航”号、“海天”号轮船同时离
(?http:?/??/?www.21cnjy.com?)开港口,各自沿一固定方向航行“远航”号每小时航行16海里,“海天”号每小时航行12海里,它们离开港口一个半小时后相距30海里,如果知道“远航”号沿东北方向航行,能知道“海天”号沿哪个方向航行吗?【版权所有:21教育】
【提示】我们可以根据题意画出如图所示的图形,可以看到,由于“远航”号的航向已知,如果求出两艘轮船所成的角,就能知道“海天”号的航向了.21教育名师原创作品
解:根据题意可画出上图,
(?http:?/??/?www.21cnjy.com?/??)
PQ=16×1.5=24,PR=12×1.5=18,QR=30,
在△PQR中,
,
∴
.
∴
△PQR是直角三角形且∠RPQ=90°.
又∵
“远航”号沿东北方向航行,可知∠QPN=45°,
∴
∠RPN=45°.
由此可知“海天”号沿西北方向航行.也可沿东南方向航行.
【提示】根据勾股定理的逆定理,可判断一个角是不是90°,这里需注意与东北方向成90°角的有两个方向,即西北方向或东南方向.21世纪教育网版权所有
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
第二讲
一定是直角三角形吗
【学习目标】
能够根据三角形三边长或某些线段之间的关系判定一个三角形是否为直角三角形.
【知识结构】
(?http:?/??/?www.21cnjy.com?/??)
【考点总结】
一、勾股定理的逆定理
(1)勾股定理的逆定理的内容:如果三角形的三边长a,b,c满足a2+b2=c2,那么这个三角形是直角三角形.
(2)勾股定理的逆定理的释疑:不少
(?http:?/??/?www.21cnjy.com?)的同学对知道三角形三边满足a2+b2=c2能得到直角三角形这样的一种结论持有怀疑的态度,其实通过三角形的全等可以很简单地证明出来.比如:如果在△ABC中,AB=c,BC=a,CA=b,并且满足a2+b2=c2
(如图所示),那么∠C=90°.2·1·c·n·j·y
(?http:?/??/?www.21cnjy.com?/??)
作△A1B1C1,使∠C1=90°,B1C1=a,C1A1=b,则A1B=a2+b2.
∵a2+b2=c2,∴A1B1=c(A1B1>0).
在△ABC和△A1B1C1中,
∵BC=a=B1C1,CA=b=C1A1,AB=c=A1B1,
∴△ABC≌△A1B1C1.
∴∠C=∠C1=90°.
辨误区
勾股定理的逆定理的条件
(1)不能说成在直角三角形中,因为还没有确定直角三角形,当然也不能说“斜边”和“直角边”.
(2)当满足a2+b2=c2时,c是斜边,∠C是直角.
利用勾股定理的逆定理判断一个三角形是否为
(?http:?/??/?www.21cnjy.com?)直角三角形的思路是:先确定最长边,算出最长边的平方及另两边的平方和,如果最长边的平方与另两边的平方和相等,则此三角形为直角三角形.
对啊!到目前为止判定直角三角形的方法有:
①说明三角形中有一个直角;
②说明三角形中有两边互相垂直;
③勾股定理的逆定理.
二、勾股定理的逆定理与勾股定理的关系
勾股定理是通过“形”的状态来反映“数”的关系的,而勾股定理的逆定理是通过“数”的关系来反映“形”的状态的.21cnjy.com
(1)勾股定理是直角三角形的性质定理,勾股定理的逆定理是直角三角形的判定定理,二者是互逆的.
(2)联系:①两者都与a2+b2=c2有关,②两者所讨论的问题都是直角三角形问题.
(3)区别:勾股定理是以“
(?http:?/??/?www.21cnjy.com?)一个三角形是直角三角形”为条件,进而得到这个直角三角形三边的数量关系“a2+b2=c2”;勾股定理的逆定理则是以“一个三角形的三边满足a2+b2=c2”为条件,进而得到这个三角形是“直角三角形”.www-2-1-cnjy-com
(4)二者关系可列表如下:
定理
勾股定理
勾股定理的逆定理
内容
如果直角三角形的两直角边长分别为a,b,斜边长为c,那么a2+b2=c2
如果三角形的三边长a,b,c满足a2+b2=c2,那么这个三角形是直角三角形
题设
直角三角形的两直角边长分别为a,b,斜边长为c
三角形的三边长a,b,c满足a2+b2=c2
结论
a2+b2=c2
三角形是直角三角形
用途
是直角三角形的一个性质
判定直角三角形的一种方法
三、勾股数
勾股数:满足a2+b2=c2的三个正整数,称为勾股数.
(1)由定义可知,一组数是勾股数必须满足两个条件:①满足a2+b2=c2;②都是正整数.两者缺一不可.
(2)将一组勾股数同时扩大或缩
(?http:?/??/?www.21cnjy.com?)小相同的倍数所得的数仍满足a2+b2=c2(但不一定是勾股数),以它们为边长的三角形是直角三角形,比如以0.3
cm,0.4
cm,0.5
cm为边长的三角形是直角三角形.
四、勾股定理的逆定理的应用
勾股定理的逆定理在解决实
(?http:?/??/?www.21cnjy.com?)际问题中有着广泛的应用,可以用它来判定是不是直角.家里建房时,常需要在现场画出直角,在没有测量角的仪器的情况下,工人师傅常常利用勾股定理的逆定理作出直角.
五、利用非负数的性质判定三角形的形状
在由一个等式求三角形的三边长时,往往先把等式
(?http:?/??/?www.21cnjy.com?)化为a2+b2+c2=0的形式,再由a=0,b=0,c=0,求得三角形三边之长,利用计算来判断△ABC是否是直角三角形.【来源:21·世纪·教育·网】
谈重点
判定三角形的形状
由条件等式来判断三角形的形状,就是将已知的条件等式变形,再根据它的结构特点,得出a,b,c的关系,从而判断三角形的形状.2-1-c-n-j-y
六、勾股定理及其逆定理的综合应用
(1)利用勾股定理解决生活中的实际问题时,关键是利用转化的思想把实际问题转化为数学模型(直角三角形)来解决.21
cnjy
com
(2)综合运用勾股定理及其逆定理
(?http:?/??/?www.21cnjy.com?),将不规则图形转化为规则图形是常用的数学方法,在这里,一方面要熟记常用的勾股数;另一方面要注意到:如果一个三角形的三边长已知或具有某些比例关系,那么就可以用勾股定理的逆定理去验证其是否是直角三角形.
【来源:21cnj
y.co
m】
【例题讲解】
【类型】一、原命题与逆命题
例1、写出下列原命题的逆命题并判断是否正确
1.原命题:猫有四只脚.
2.原命题:对顶角相等.
3.原命题:线段垂直平分线上的点,到这条线段两端点的距离相等.
4.原命题:角平分线上的点,到这个角的两边距离相等.
【答案与解析】
1.
逆命题:有四只脚的是猫(不正确)
2.
逆命题:相等的角是对顶角(不正确)
3.
逆命题:到线段两端距离相等的点,在这条线段的垂直平分线上.(正确)
4.
逆命题:到角两边距离相等的点,在这个角的角平分线上.(正确)
【总结】掌握原命题与逆命题的关系.
原命题正确,逆命题未必正确;原命题不正确,其逆命题也不一定错误.www.21-cn-jy.com
【训练】下列命题中,其逆命题成立的是______________.(只填写序号)
①同旁内角互补,两直线平行;
②如果两个角是直角,那么它们相等;
③如果两个实数相等,那么它们的平方相等;
④如果三角形的三边长满足,那么这个三角形是直角三角形.
【答案】①④
提示:①的逆命题“两直线平行,同旁内角互补”显然正确;②的逆命题“如果两个角相等,那么它们是直角”很明显是错误的;③的逆命题“如果两个实数的平方相等,那么这两个实数相等”,两个实数可以互为相反数,所以该命题不正确;④的逆命题“如果三角形是直角三角形,那么三角形的三边长满足”也是正确的.【出处:21教育名师】
【类型】二、勾股定理的逆定理
例2、判断由线段组成的三角形是不是直角三角形.
(1)=7,=24,=25;
(2)=,=1,=;
(3),,();
【知识点提示】判断三条线段能否组成直角
(?http:?/??/?www.21cnjy.com?)三角形,关键是运用勾股定理的逆定理:看较短的两条线段的平方和是否等于最长线段的平方.若是,则为直角三角形,反之,则不是直角三角形.
【答案与解析】
解:(1)∵
,,
∴
.
∴
由线段组成的三角形是直角三角形.
(2)∵
,,,
∴
.
∴
由线段组成的三角形不是直角三角形.
(3)∵
,
∴
,.
∵,
,
∴
.
∴
由线段组成的三角形是直角三角形.
【提示】解此类题的关键是准确地判断哪一条边最大,然后再利用勾股定理的逆定理进行判断,即首先确定最大边,然后验证与是否具有相等关系,再根据结果判断是否为直角三角形.
【训练】判断以线段为边的△ABC是不是直角三角形,其中,,.
解:由于,因此为最大边,只需看是否等于即可.
∵
,,,∴
,
∴
以线段为边能构成以为斜边的直角三角形.
【训练】下列四组数:①5,12,
(?http:?/??/?www.21cnjy.com?)13;②7,24,25;③1,2,4;④5,6,8.其中可以为直角三角形三边长的有
.(把所有你认为正确的序号都写上)21教育网
【答案】①②;
解:①∵52+122=132,能构成直角三角形;
②72+242=252,能构成直角三角形;
③12+22≠42,不能构成直角三角形;
④52+62≠82,不能构成直角三角形.
所以①②.
故答案为:①②.
例3、
已知:如图,四边形ABCD中,AB⊥BC,AB=1,BC=2,CD=2,AD=3,求四边形ABCD的面积.
(?http:?/??/?www.21cnjy.com?/??)
解:连接AC.
∵∠ABC=90°,AB=1,BC=2,
∴AC==,
在△ACD中,AC2+CD2=5+4=9=AD2,
∴△ACD是直角三角形,
∴S四边形ABCD=AB?BC+AC?CD,
=×1×2+××2,
=1+.
故四边形ABCD的面积为1+.
(?http:?/??/?www.21cnjy.com?/??)
【提示】本题考查的是勾股定理的逆定理及三角形的面积,能根据勾股定理的逆定理判断出△ACD的形状是解答此题的关键.21·cn·jy·com
【训练】如图所示,在梯形ABCD中
(?http:?/??/?www.21cnjy.com?),AB∥CD,∠A=90°,AB=2,BC=3,CD=1,E是AD中点,试判断EC与EB的位置关系,并写出推理过程.21·世纪
教育网
(?http:?/??/?www.21cnjy.com?/??)
解:EC⊥EB.
过点C作CF⊥AB于F,则四边形AFCD是矩形,
在Rt△BCF中,可得CF=.
(?http:?/??/?www.21cnjy.com?/??)
则AD=CF=,故DE=AE=AD=.
在Rt△ABE和Rt△DCE中,
,.
∴
.
∵
BC=3,∴
.
∴
∠CEB=90°,∴
EB⊥EC.
【类型】三、勾股定理逆定理的实际应用
例4、“远航”号、“海天”号轮船同时离
(?http:?/??/?www.21cnjy.com?)开港口,各自沿一固定方向航行“远航”号每小时航行16海里,“海天”号每小时航行12海里,它们离开港口一个半小时后相距30海里,如果知道“远航”号沿东北方向航行,能知道“海天”号沿哪个方向航行吗?【版权所有:21教育】
【提示】我们可以根据题意画出如图所示的图形,可以看到,由于“远航”号的航向已知,如果求出两艘轮船所成的角,就能知道“海天”号的航向了.21教育名师原创作品
解:根据题意可画出上图,
(?http:?/??/?www.21cnjy.com?/??)
PQ=16×1.5=24,PR=12×1.5=18,QR=30,
在△PQR中,
,
∴
.
∴
△PQR是直角三角形且∠RPQ=90°.
又∵
“远航”号沿东北方向航行,可知∠QPN=45°,
∴
∠RPN=45°.
由此可知“海天”号沿西北方向航行.也可沿东南方向航行.
【提示】根据勾股定理的逆定理,可判断一个角是不是90°,这里需注意与东北方向成90°角的有两个方向,即西北方向或东南方向.21世纪教育网版权所有
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
