第一讲 认识无理数(考点讲解)(含答案)
文档属性
| 名称 | 第一讲 认识无理数(考点讲解)(含答案) | 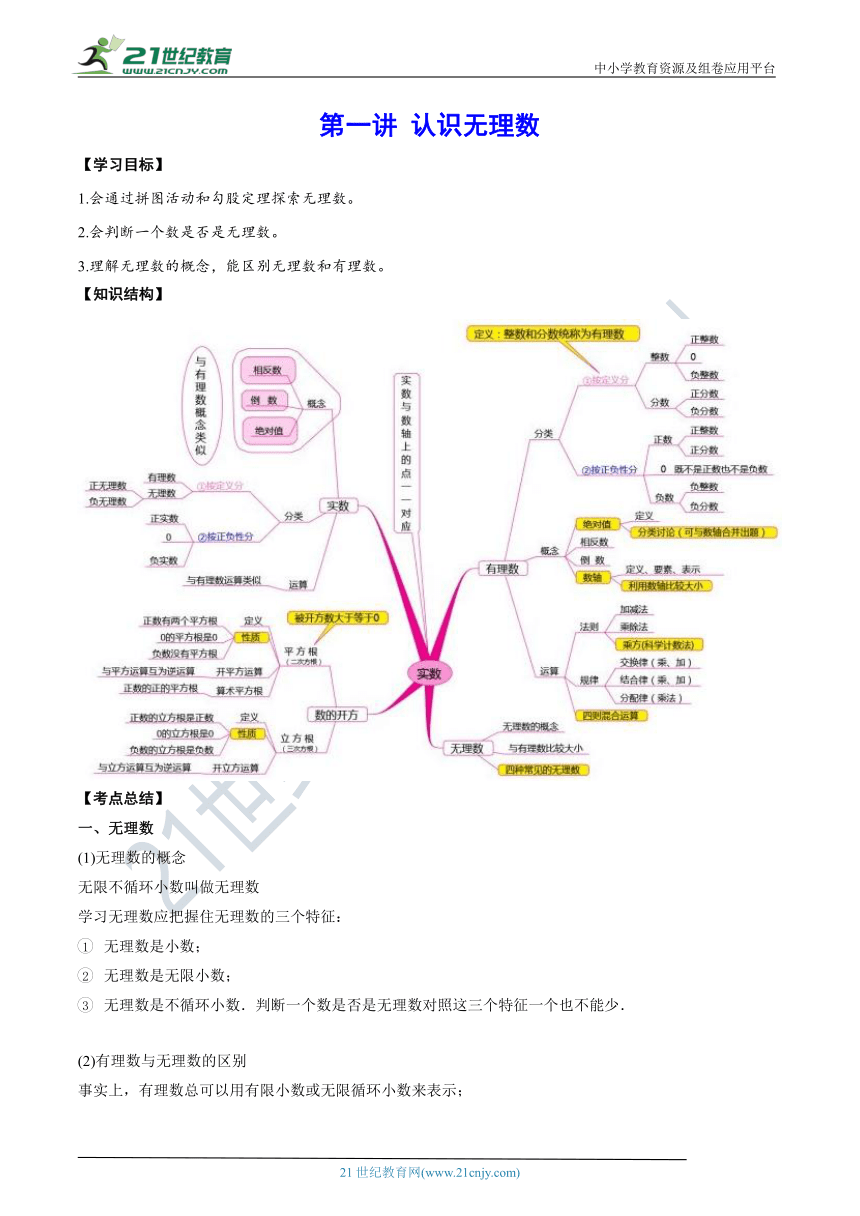 | |
| 格式 | doc | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-19 10:23:49 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
第一讲
认识无理数
【学习目标】
1.会通过拼图活动和勾股定理探索无理数。
2.会判断一个数是否是无理数。
3.理解无理数的概念,能区别无理数和有理数。
【知识结构】
(?http:?/??/?www.21cnjy.com?/??)
【考点总结】
一、无理数
(1)无理数的概念
无限不循环小数叫做无理数
学习无理数应把握住无理数的三个特征:21世纪教育网
1
无理数是小数;
2
无理数是无限小数;
3
无理数是不循环小数.判断一个数是否是无理数对照这三个特征一个也不能少.
(2)有理数与无理数的区别
事实上,有理数总可以用有限小数或无限循环小数来表示;
反过来,任何有限小数或无限循环小数也都是有理数.
如3可看做3.0这样的有限小数,也可以化为这样的分数形式;
无限循环小数都可以化为分数,
如:3.14可化为3.
有理数与无理数的主要区别:
①无理数是无限不循环小数,有理数是有限小数或无限循环小数;21世纪教育网
②任何一个有理数都可以化为分数的形式,而无理数不能.
二、无理数近似值的估算方法
要估算无理数的近似值,第一步应确定被估算无理数的整数取值范围;第二步以较小整数逐步开始加0.1(或以较大整数逐步开始减0.1),并求其平方,确定被估算数的十分位;…;如此继续下去,可以求出无理数的近似值.21世纪教育网版权所有
三、无理数的常见类型
判断一个数是不是无理数,关键就是看它能不能写成无限不循环的小数,无理数常见的形式主要有三种:
(1)一般的无限不循环小数,如1.414
213
56…是无理数.21世纪教育网
看似循环而实质不循环的小数,如0.101
001
000
1…(相邻两个1之间0的个数逐次增加1)是无理数.
(2)圆周率π以及含π的数,如π,2π,π+5,都是无理数.
(3)开方开不尽的数(下一节学到).
四、无理数的应用
无理数的估算用的是“夹逼法”,要注意掌握其应用特征.估算无理数的近似值,应先确定被估算无理数的整数取值范围;21cnjy.com
再以较小整数逐步开始加0.1(或以较大整数开始逐步减0.1),并求其平方确定被估算数的十分位;…;如此继续下去,可以求估算无理数的近似值.www.21-cn-jy.com
注:误差小于0.1与精确到0.1是不同的两个概念.在处理有关问题时要看清要求,再着手处理.
【例题讲解】
1、下列各数中,哪些是有理数?哪些是无理数?21世纪教育网
3.141
592
6,-,2.,6.751
755
175
551
7…(相邻7,1之间5的个数逐次加1),0,,-5.2,-.
分析:有理数指有限小数或无限循环小数,整数和分数都是有理数,无理数指无限不循环小数.
解:有理数有:3.141
592
6,-,2.,0,,-5.2;
无理数有:6.751
755
175
551
7…(相邻7,1之间5的个数逐次加1),-.
2、面积为7的正方形的边长为x,请你回答下列问题.
(1)x的整数部分是多少?
(2)把x的值精确到十分位是多少?精确到百分位呢?
(3)x是有理数吗?请简要说明理由.
解:令正方形的面积为S,则S=x2=7,当2<x<3时,4<x2<9,当2.6<x<2.7时,6.76<x2<7.29;
当2.64<x<2.65时,6.969
6<x2<7.022
5;
当2.645<x<2.646时,6.996
025<x2<7.001
316;
…
则有:
(1)x的整数部分为2.
(2)精确到十分位时,x≈2.6,精确到百分位时,x≈2.65.
(3)x不是有理数.因为没有一个整数的平方
等于7,也没有一个分数的平方等于7,另由计算可知,x是无限不循环小数.
释疑点如何四舍五入
利用四舍五入法取近似值时要比精确到的位数多考查一位.
3、下列各数,哪些是有理数?哪些是无理数?
0,,-4,0.,-,1.112
111
211…(相邻两个2之间1的个数逐次加1),3.141
592
7.
分析:1.112
111
211…(相
(?http:?/??/?www.21cnjy.com?)邻两个2之间1的个数逐次加1)为无限不循环小数,为含π的数,两者都为无理数.0,-4为整数,是有理数;0.,-,3.141
592
7为分数或可化为分数,是有理数.
解:有理数为0,-4,0.,-,3.141
592
7;无理数为,1.112
111
211…(相邻两个2之间1的个数逐次加1).21教育网
辨误区π与3.141
592
7的区别
3.141
592
7属于有限小数,不是π,要注意区分.
4、如图所示,要从离地面5
m的电线杆上的B处向地面C处拉一条钢丝绳来固定电线杆,要固定点C到A处的距离为3
m,求钢丝绳BC的长度(精确到十分位).21·cn·jy·com
(?http:?/??/?www.21cnjy.com?/??)
分析:这是现实生活中的一个常见问题,解决这个问题首先要用到勾股定理,再利用“夹逼法”估算BC的长.21世纪教育网2·1·c·n·j·y
解:由勾股定理,得BC2=AB2+AC2=34.
当5<BC<6时,25<BC2<36;
当5.8<BC<5.9时,33.64<BC2<34.81;
当5.83<BC<5.84时,33.988
9<BC2<34.105
6;
…
故当精确到十分位时,BC约为5.8
m.
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
第一讲
认识无理数
【学习目标】
1.会通过拼图活动和勾股定理探索无理数。
2.会判断一个数是否是无理数。
3.理解无理数的概念,能区别无理数和有理数。
【知识结构】
(?http:?/??/?www.21cnjy.com?/??)
【考点总结】
一、无理数
(1)无理数的概念
无限不循环小数叫做无理数
学习无理数应把握住无理数的三个特征:21世纪教育网
1
无理数是小数;
2
无理数是无限小数;
3
无理数是不循环小数.判断一个数是否是无理数对照这三个特征一个也不能少.
(2)有理数与无理数的区别
事实上,有理数总可以用有限小数或无限循环小数来表示;
反过来,任何有限小数或无限循环小数也都是有理数.
如3可看做3.0这样的有限小数,也可以化为这样的分数形式;
无限循环小数都可以化为分数,
如:3.14可化为3.
有理数与无理数的主要区别:
①无理数是无限不循环小数,有理数是有限小数或无限循环小数;21世纪教育网
②任何一个有理数都可以化为分数的形式,而无理数不能.
二、无理数近似值的估算方法
要估算无理数的近似值,第一步应确定被估算无理数的整数取值范围;第二步以较小整数逐步开始加0.1(或以较大整数逐步开始减0.1),并求其平方,确定被估算数的十分位;…;如此继续下去,可以求出无理数的近似值.21世纪教育网版权所有
三、无理数的常见类型
判断一个数是不是无理数,关键就是看它能不能写成无限不循环的小数,无理数常见的形式主要有三种:
(1)一般的无限不循环小数,如1.414
213
56…是无理数.21世纪教育网
看似循环而实质不循环的小数,如0.101
001
000
1…(相邻两个1之间0的个数逐次增加1)是无理数.
(2)圆周率π以及含π的数,如π,2π,π+5,都是无理数.
(3)开方开不尽的数(下一节学到).
四、无理数的应用
无理数的估算用的是“夹逼法”,要注意掌握其应用特征.估算无理数的近似值,应先确定被估算无理数的整数取值范围;21cnjy.com
再以较小整数逐步开始加0.1(或以较大整数开始逐步减0.1),并求其平方确定被估算数的十分位;…;如此继续下去,可以求估算无理数的近似值.www.21-cn-jy.com
注:误差小于0.1与精确到0.1是不同的两个概念.在处理有关问题时要看清要求,再着手处理.
【例题讲解】
1、下列各数中,哪些是有理数?哪些是无理数?21世纪教育网
3.141
592
6,-,2.,6.751
755
175
551
7…(相邻7,1之间5的个数逐次加1),0,,-5.2,-.
分析:有理数指有限小数或无限循环小数,整数和分数都是有理数,无理数指无限不循环小数.
解:有理数有:3.141
592
6,-,2.,0,,-5.2;
无理数有:6.751
755
175
551
7…(相邻7,1之间5的个数逐次加1),-.
2、面积为7的正方形的边长为x,请你回答下列问题.
(1)x的整数部分是多少?
(2)把x的值精确到十分位是多少?精确到百分位呢?
(3)x是有理数吗?请简要说明理由.
解:令正方形的面积为S,则S=x2=7,当2<x<3时,4<x2<9,当2.6<x<2.7时,6.76<x2<7.29;
当2.64<x<2.65时,6.969
6<x2<7.022
5;
当2.645<x<2.646时,6.996
025<x2<7.001
316;
…
则有:
(1)x的整数部分为2.
(2)精确到十分位时,x≈2.6,精确到百分位时,x≈2.65.
(3)x不是有理数.因为没有一个整数的平方
等于7,也没有一个分数的平方等于7,另由计算可知,x是无限不循环小数.
释疑点如何四舍五入
利用四舍五入法取近似值时要比精确到的位数多考查一位.
3、下列各数,哪些是有理数?哪些是无理数?
0,,-4,0.,-,1.112
111
211…(相邻两个2之间1的个数逐次加1),3.141
592
7.
分析:1.112
111
211…(相
(?http:?/??/?www.21cnjy.com?)邻两个2之间1的个数逐次加1)为无限不循环小数,为含π的数,两者都为无理数.0,-4为整数,是有理数;0.,-,3.141
592
7为分数或可化为分数,是有理数.
解:有理数为0,-4,0.,-,3.141
592
7;无理数为,1.112
111
211…(相邻两个2之间1的个数逐次加1).21教育网
辨误区π与3.141
592
7的区别
3.141
592
7属于有限小数,不是π,要注意区分.
4、如图所示,要从离地面5
m的电线杆上的B处向地面C处拉一条钢丝绳来固定电线杆,要固定点C到A处的距离为3
m,求钢丝绳BC的长度(精确到十分位).21·cn·jy·com
(?http:?/??/?www.21cnjy.com?/??)
分析:这是现实生活中的一个常见问题,解决这个问题首先要用到勾股定理,再利用“夹逼法”估算BC的长.21世纪教育网2·1·c·n·j·y
解:由勾股定理,得BC2=AB2+AC2=34.
当5<BC<6时,25<BC2<36;
当5.8<BC<5.9时,33.64<BC2<34.81;
当5.83<BC<5.84时,33.988
9<BC2<34.105
6;
…
故当精确到十分位时,BC约为5.8
m.
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
