吉林省吉林市第二中学2020-2021学年高二下学期期中考试数学(文)试题(Word版含答案)
文档属性
| 名称 | 吉林省吉林市第二中学2020-2021学年高二下学期期中考试数学(文)试题(Word版含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 557.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-18 17:06:24 | ||
图片预览


文档简介
吉林二中2020-2021学年度下学期期中考试
高二数学(文)试卷
第Ⅰ卷
说明:1、本试卷分第I试卷(选择题)和第II卷(非选择题)两部分;
2、满分150分,考试时间
120分钟。
1、选择题(共12题,每题5分,共60分)
1.设集合,,则(
)
A.
B.
C.
D.
2.已知,若为纯虚数(为虚数单位),则的值为
(
)
A.
B.
C.
D.
3.已知,则的值为(
)
A.-
B.
C.-
D.
4.已知,则等于(
)
A.
B.
C.
D.
5.若向量,且与共线,则实数的值为(
)
A.
B.
C.
D.
6.在数列中,,,则(
)
A.
B.
C.
D.3
1
2
3
4
5
6.5
4
1
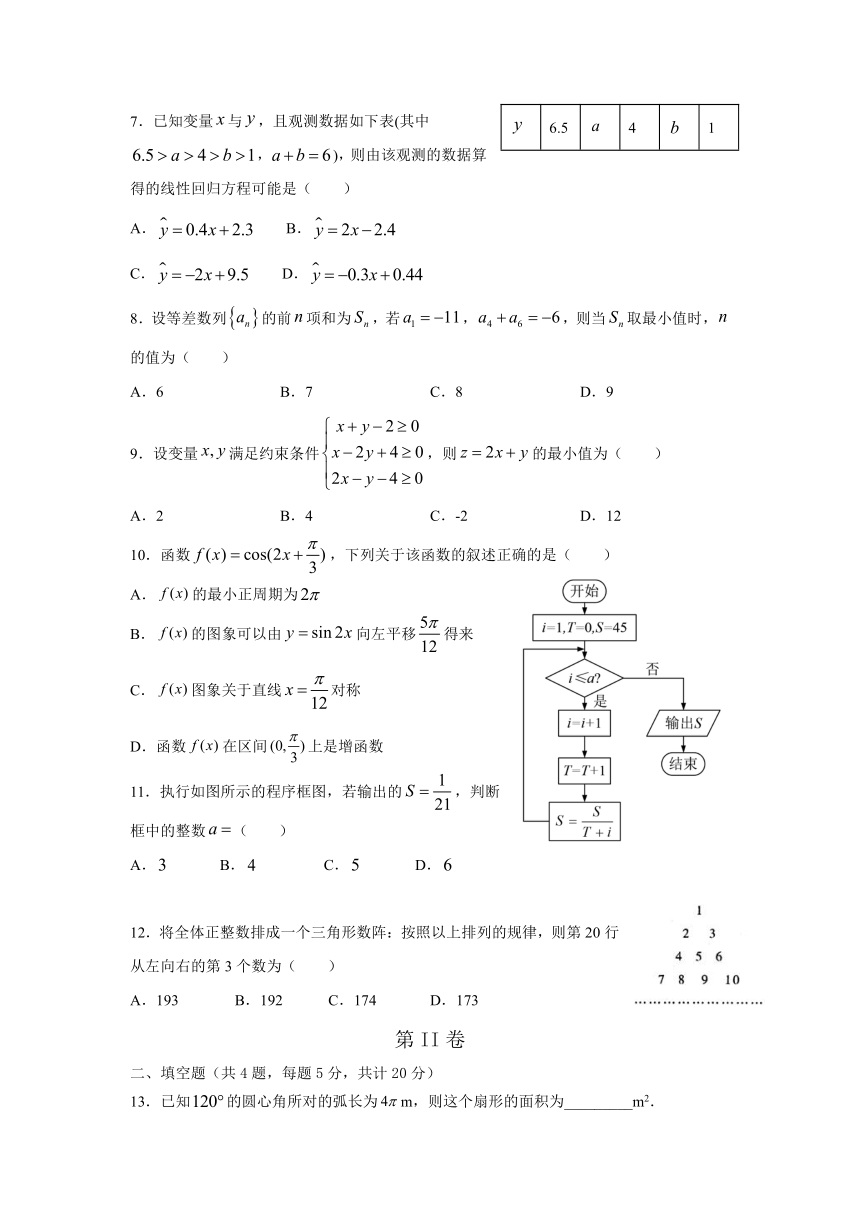
7.已知变量与,且观测数据如下表(其中,),则由该观测的数据算得的线性回归方程可能是(
)
A.
B.
C.
D.
8.设等差数列的前项和为,若,,则当取最小值时,的值为(
)
A.6
B.7
C.8
D.9
9.设变量满足约束条件,则的最小值为(
)
A.2
B.4
C.-2
D.12
10.函数,下列关于该函数的叙述正确的是(
)
A.的最小正周期为
B.的图象可以由向左平移得来
C.图象关于直线对称
D.函数在区间上是增函数
11.执行如图所示的程序框图,若输出的,判断框中的整数(
)
A.
B.
C.
D.
12.将全体正整数排成一个三角形数阵:按照以上排列的规律,则第20行从左向右的第3个数为( )
A.193
B.192
C.174
D.173
第II卷
二、填空题(共4题,每题5分,共计20分)
13.已知的圆心角所对的弧长为m,则这个扇形的面积为_________m2.
14.已知实数,,则的最小值为_________
.
15.一艘船以32海里/小时的速度向正北航行,在处看灯塔在船的北偏东,半小时后航行到处,在处看到灯塔在船的北偏东,则灯塔与点的距离为______海里.
16.若不等式对一切恒成立,则的取值范围是_________.
三、解答题(共6题,17题10分,其余每题12分,共计70分)
17.已知等差数列满足,前项和.
(1)求的通项公式;
(2)设等比数列满足,,求的前项和.
18.已知函数
(1)求函数f(x)的单调递增区间;
(2)函数f(x)的图象上所有点的横坐标扩大到原来的2倍,再向右平移个单位长度,得g(x)的图象,求函数y=g(x)在x∈[0,π]上的最大值及最小值.
19.某校党委组织党员老师参加“学习强国”的知识竞赛,从参加竞赛的党员中抽出50人,将其绩(均为整数)分成六段[40,
50),[50,60),...
[90,
100]后画出如下部分频率分布直方图.观察图给出的信息,回答下列问题:
(1)求第五小组的频率,估计这次竞赛成绩的平均分;
(2)从成绩低于60分的人中随机选取2人,至少有一人成绩在[40,
50)内的概率.
20.在中,角A,B,C的对边分别为a,b,c,且.
(1)求角C;
(2)若,求的面积.
21.若数列的前项和为,点在函数的图象上.
(1)求数列的通项公式;
(2)设,求数列的前项和.
22.已知,
(1)若的图象有与轴平行的切线,求的取值范围;
(2)若在时取得极值,且恒成立,求的取值范围.
高二数学(文)答案
选择题(每题5分,共60分)
BA
BA
BACA
BBBA
二、填空题(每题5分,共20分)
13.
14.
15.
16.
三、解答题(17题10分,其余12分)
17.(10分)(1)得,故通项公式为.
(2)由(1)得,,设的公比为,则,得,
故的前项和.
18.(12分)∵,
∴函数f(x)的单调递增区间为:.
(2),∵x∈[0,π]得:,
∴当x=0时,有最小值,
当时,有最大值1.
19.(12分)第五小组的频率0.18.
这次竞赛成绩的平均分为74;
(2)成绩低于60分的同学在之间的有3人,在之间的有3人,
则,∴,
20.(12分)(1)由正弦定理得,即,
所以,,所以;
(2),.
21.(12分)解:(1)当,.
又因为满足,所以;
(2),
所以.
22.(12分)(1),由己知有实数解,∴,故.
(2)由题意是方程的一个根,设另一根为,
则,∴,∴,,
当时,;当时,;当时,,
∴当时,有极大值;又,,
即当时,的最大值为,
∵对时,恒成立,∴,∴或,
高二数学(文)试卷
第Ⅰ卷
说明:1、本试卷分第I试卷(选择题)和第II卷(非选择题)两部分;
2、满分150分,考试时间
120分钟。
1、选择题(共12题,每题5分,共60分)
1.设集合,,则(
)
A.
B.
C.
D.
2.已知,若为纯虚数(为虚数单位),则的值为
(
)
A.
B.
C.
D.
3.已知,则的值为(
)
A.-
B.
C.-
D.
4.已知,则等于(
)
A.
B.
C.
D.
5.若向量,且与共线,则实数的值为(
)
A.
B.
C.
D.
6.在数列中,,,则(
)
A.
B.
C.
D.3
1
2
3
4
5
6.5
4
1
7.已知变量与,且观测数据如下表(其中,),则由该观测的数据算得的线性回归方程可能是(
)
A.
B.
C.
D.
8.设等差数列的前项和为,若,,则当取最小值时,的值为(
)
A.6
B.7
C.8
D.9
9.设变量满足约束条件,则的最小值为(
)
A.2
B.4
C.-2
D.12
10.函数,下列关于该函数的叙述正确的是(
)
A.的最小正周期为
B.的图象可以由向左平移得来
C.图象关于直线对称
D.函数在区间上是增函数
11.执行如图所示的程序框图,若输出的,判断框中的整数(
)
A.
B.
C.
D.
12.将全体正整数排成一个三角形数阵:按照以上排列的规律,则第20行从左向右的第3个数为( )
A.193
B.192
C.174
D.173
第II卷
二、填空题(共4题,每题5分,共计20分)
13.已知的圆心角所对的弧长为m,则这个扇形的面积为_________m2.
14.已知实数,,则的最小值为_________
.
15.一艘船以32海里/小时的速度向正北航行,在处看灯塔在船的北偏东,半小时后航行到处,在处看到灯塔在船的北偏东,则灯塔与点的距离为______海里.
16.若不等式对一切恒成立,则的取值范围是_________.
三、解答题(共6题,17题10分,其余每题12分,共计70分)
17.已知等差数列满足,前项和.
(1)求的通项公式;
(2)设等比数列满足,,求的前项和.
18.已知函数
(1)求函数f(x)的单调递增区间;
(2)函数f(x)的图象上所有点的横坐标扩大到原来的2倍,再向右平移个单位长度,得g(x)的图象,求函数y=g(x)在x∈[0,π]上的最大值及最小值.
19.某校党委组织党员老师参加“学习强国”的知识竞赛,从参加竞赛的党员中抽出50人,将其绩(均为整数)分成六段[40,
50),[50,60),...
[90,
100]后画出如下部分频率分布直方图.观察图给出的信息,回答下列问题:
(1)求第五小组的频率,估计这次竞赛成绩的平均分;
(2)从成绩低于60分的人中随机选取2人,至少有一人成绩在[40,
50)内的概率.
20.在中,角A,B,C的对边分别为a,b,c,且.
(1)求角C;
(2)若,求的面积.
21.若数列的前项和为,点在函数的图象上.
(1)求数列的通项公式;
(2)设,求数列的前项和.
22.已知,
(1)若的图象有与轴平行的切线,求的取值范围;
(2)若在时取得极值,且恒成立,求的取值范围.
高二数学(文)答案
选择题(每题5分,共60分)
BA
BA
BACA
BBBA
二、填空题(每题5分,共20分)
13.
14.
15.
16.
三、解答题(17题10分,其余12分)
17.(10分)(1)得,故通项公式为.
(2)由(1)得,,设的公比为,则,得,
故的前项和.
18.(12分)∵,
∴函数f(x)的单调递增区间为:.
(2),∵x∈[0,π]得:,
∴当x=0时,有最小值,
当时,有最大值1.
19.(12分)第五小组的频率0.18.
这次竞赛成绩的平均分为74;
(2)成绩低于60分的同学在之间的有3人,在之间的有3人,
则,∴,
20.(12分)(1)由正弦定理得,即,
所以,,所以;
(2),.
21.(12分)解:(1)当,.
又因为满足,所以;
(2),
所以.
22.(12分)(1),由己知有实数解,∴,故.
(2)由题意是方程的一个根,设另一根为,
则,∴,∴,,
当时,;当时,;当时,,
∴当时,有极大值;又,,
即当时,的最大值为,
∵对时,恒成立,∴,∴或,
同课章节目录
