吉林省吉林市第二中学2020-2021学年高二下学期期末考试数学(文)试题(Word版含答案)
文档属性
| 名称 | 吉林省吉林市第二中学2020-2021学年高二下学期期末考试数学(文)试题(Word版含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 744.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-18 00:00:00 | ||
图片预览



文档简介
吉林二中2020-2021学年度下学期期末考试
高二数学(文)试卷
第Ⅰ卷
说明:1、本试卷分第I试卷(选择题)和第II卷(非选择题)两部分;
2、满分150分,考试时间
120分钟。
1、选择题(共12题,每题5分,共60分)
1.设集合,,则(
)
A.
B.
C.
D.
2.命题“,x2-2x+120”的否定为(
)
A.,x2-2x+120
B.,
C.,x2-2x+120
D.,
3.已知,且,则(
)
A.
B.
C.
D.
4.已知,则和同向的单位向量是(
)
A.
B.
C.
D.
5.不等式成立的一个充分不必要条件是(
)
A.
B.
C.
D.
6.直线:与:平行,则(
)
A.
B.
C.2
D.0
7.与圆都相切的直线有(
)
A.1条
B.2条
C.3条
D.4条
8.某几何体的三视图如图所示,则该几何体的表面积为(
)
A.
B.
C.
D.
9.一只小虫在边长为的正方形内部爬行,到各顶点的距离不小于时为安全区域,则小虫在安全区域内爬行的概率是(
)
A.
B.
C.
D.
零件数(个)
2
3
4
5
加工时间(分钟)
26
49
54
10.一车间为规定工时定额,需要确定加工
零件所花费的时间,为此进行了4次试验,测得的数据如图:
根据上表可得回归方程,则实数的值为(
)
A.37.3
B.38
C.39
D.39.5
11.当时,函数的
A.最大值是1,最小值是
B.最大值是1,最小值是
C.最大值是2,最小值是
D.最大值是2,最小值是
12.某人于年月日去银行存款元,存的是一年定期储蓄,年月日将到期存款的本息一起取出再加元之后还存一年定期储蓄,此后每年的月日他都按照同样的方法在银行取款和存款.设银行一年定期储蓄的年利率不变,则到年月日他将所有的本息全部取出时,取出的钱共有(
)
A.元
B.元
C.元
D.元
第II卷
二、填空题(共4题,每题5分,共计20分)
13.已知函数的图象过定点P,则点P的坐标为___________.
14.已知正实数a,b满足,则的最小值为___________.
15.若x,y满足约束条件,则的最小值为___________.
16.若a>0且a≠1,且函数在R上单调递増,那么a的取值范围是________.
三、解答题(共6题,17题10分,其余每题12分,共计70分)
17.
已知等差数列中,.
(1)求的通项公式;
(2)求的前项和的最大值.
18.△ABC的内角A,B,C的对边分别为a,b,c,已知=.
(1)求B;
(2)若b=3,,求△ABC的面积.
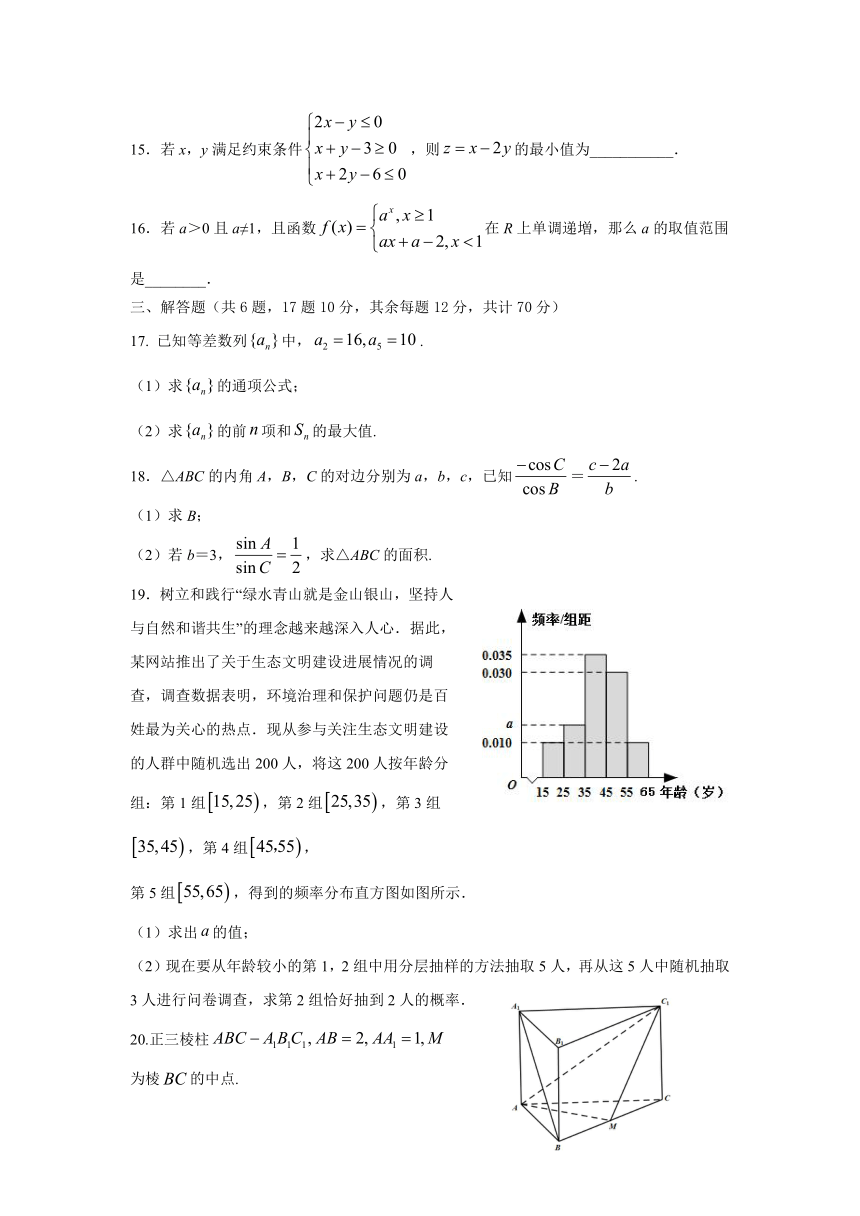
19.树立和践行“绿水青山就是金山银山,坚持人与自然和谐共生”的理念越来越深入人心.据此,某网站推出了关于生态文明建设进展情况的调查,调查数据表明,环境治理和保护问题仍是百姓最为关心的热点.现从参与关注生态文明建设的人群中随机选出200人,将这200人按年龄分组:第1组,第2组,第3组,第4组,
第5组,得到的频率分布直方图如图所示.
(1)求出的值;
(2)现在要从年龄较小的第1,2组中用分层抽样的方法抽取5人,再从这5人中随机抽取3人进行问卷调查,求第2组恰好抽到2人的概率.
20.正三棱柱
为棱的中点.
(1)证明:平面;
(2)证明:平面平面;
(3)求直线与平面所成角的正弦值.
21.已知点,,以为直径的圆记为圆.
(1)求圆的方程
(2)过点的直线与圆交于,两点,且,求直线的方程.
22.已知.
(1)若不等式的解集为,求实数、的值;
(2)若时,对于任意的实数,都有,求的取值范围.
高二数学(文)答案
选择题(每题5分,共60分)
ABBA
DCCC
DCDD
二、填空题(每题5分,共20分)
13.
(
14.
9
15.
-6
16.
(1,2]
三、解答题(17题10分,其余12分)
17.(10分)解:(1)等差数列中,
,
,解得,,
的通项公式.
(2),,
的前项和.
当或时,前项和的最大值90.
18.(12分)(1)由正弦定理,得,
所以
,即
,所以
又因为,所以,所以,
又因为,所以
,因为为三角形内角,所以.
(2)因为,所以,
所以由余弦定理,得,即,
所以,
所以△ABC的面积为.
19.(12分)(1)由,得
(2)第1,2组抽取的人数分别为20人,30人,从第1,2组中用分层抽样的方法抽取5人,
则第1,2组抽取的人数分别为2人,3人,分别记为.
设从5人中随机抽取3人,为,
共10个基本事件,
其中第2组恰好抽到2人包含,
共6个基本事件,
从而第2组抽到2人的概率
20.(12分)(1)证明:如图,连接交于点,则为的中点,
的中点,,
平面,平面,平面
.
(2)证明:为正三角形,为的中点,
,平面,,
平面,平面且,
平面,
平面,平面平面
.
(3)平面平面,且交线为,
在平面内,作,则平面
,
,即为直线与平面所成角,
在中,,
,
直线与平面所成角的正弦值为.
21.(12分)(1)由题知的中点,半径.
所以圆的方程为.
(2)由题意可知直线的斜率存在,设直线的方程为,
则圆心到直线的距离,
由题知弦心距为,所以;
解方程得:或
所以直线的方程为或.
22.(12分)(1)因为的解集为,,
所以方程的两根为、,
故,解得,
经检验:当、时,不等式的解集为.
(2)当时,,
对于任意的实数,都有,
即对于任意的实数,都有,
令,
当时,恒成立;
当时,函数是增函数,即,解得;
当时,函数是减函数,即,解得,
综上所述,,的取值范围为.
高二数学(文)试卷
第Ⅰ卷
说明:1、本试卷分第I试卷(选择题)和第II卷(非选择题)两部分;
2、满分150分,考试时间
120分钟。
1、选择题(共12题,每题5分,共60分)
1.设集合,,则(
)
A.
B.
C.
D.
2.命题“,x2-2x+120”的否定为(
)
A.,x2-2x+120
B.,
C.,x2-2x+120
D.,
3.已知,且,则(
)
A.
B.
C.
D.
4.已知,则和同向的单位向量是(
)
A.
B.
C.
D.
5.不等式成立的一个充分不必要条件是(
)
A.
B.
C.
D.
6.直线:与:平行,则(
)
A.
B.
C.2
D.0
7.与圆都相切的直线有(
)
A.1条
B.2条
C.3条
D.4条
8.某几何体的三视图如图所示,则该几何体的表面积为(
)
A.
B.
C.
D.
9.一只小虫在边长为的正方形内部爬行,到各顶点的距离不小于时为安全区域,则小虫在安全区域内爬行的概率是(
)
A.
B.
C.
D.
零件数(个)
2
3
4
5
加工时间(分钟)
26
49
54
10.一车间为规定工时定额,需要确定加工
零件所花费的时间,为此进行了4次试验,测得的数据如图:
根据上表可得回归方程,则实数的值为(
)
A.37.3
B.38
C.39
D.39.5
11.当时,函数的
A.最大值是1,最小值是
B.最大值是1,最小值是
C.最大值是2,最小值是
D.最大值是2,最小值是
12.某人于年月日去银行存款元,存的是一年定期储蓄,年月日将到期存款的本息一起取出再加元之后还存一年定期储蓄,此后每年的月日他都按照同样的方法在银行取款和存款.设银行一年定期储蓄的年利率不变,则到年月日他将所有的本息全部取出时,取出的钱共有(
)
A.元
B.元
C.元
D.元
第II卷
二、填空题(共4题,每题5分,共计20分)
13.已知函数的图象过定点P,则点P的坐标为___________.
14.已知正实数a,b满足,则的最小值为___________.
15.若x,y满足约束条件,则的最小值为___________.
16.若a>0且a≠1,且函数在R上单调递増,那么a的取值范围是________.
三、解答题(共6题,17题10分,其余每题12分,共计70分)
17.
已知等差数列中,.
(1)求的通项公式;
(2)求的前项和的最大值.
18.△ABC的内角A,B,C的对边分别为a,b,c,已知=.
(1)求B;
(2)若b=3,,求△ABC的面积.
19.树立和践行“绿水青山就是金山银山,坚持人与自然和谐共生”的理念越来越深入人心.据此,某网站推出了关于生态文明建设进展情况的调查,调查数据表明,环境治理和保护问题仍是百姓最为关心的热点.现从参与关注生态文明建设的人群中随机选出200人,将这200人按年龄分组:第1组,第2组,第3组,第4组,
第5组,得到的频率分布直方图如图所示.
(1)求出的值;
(2)现在要从年龄较小的第1,2组中用分层抽样的方法抽取5人,再从这5人中随机抽取3人进行问卷调查,求第2组恰好抽到2人的概率.
20.正三棱柱
为棱的中点.
(1)证明:平面;
(2)证明:平面平面;
(3)求直线与平面所成角的正弦值.
21.已知点,,以为直径的圆记为圆.
(1)求圆的方程
(2)过点的直线与圆交于,两点,且,求直线的方程.
22.已知.
(1)若不等式的解集为,求实数、的值;
(2)若时,对于任意的实数,都有,求的取值范围.
高二数学(文)答案
选择题(每题5分,共60分)
ABBA
DCCC
DCDD
二、填空题(每题5分,共20分)
13.
(
14.
9
15.
-6
16.
(1,2]
三、解答题(17题10分,其余12分)
17.(10分)解:(1)等差数列中,
,
,解得,,
的通项公式.
(2),,
的前项和.
当或时,前项和的最大值90.
18.(12分)(1)由正弦定理,得,
所以
,即
,所以
又因为,所以,所以,
又因为,所以
,因为为三角形内角,所以.
(2)因为,所以,
所以由余弦定理,得,即,
所以,
所以△ABC的面积为.
19.(12分)(1)由,得
(2)第1,2组抽取的人数分别为20人,30人,从第1,2组中用分层抽样的方法抽取5人,
则第1,2组抽取的人数分别为2人,3人,分别记为.
设从5人中随机抽取3人,为,
共10个基本事件,
其中第2组恰好抽到2人包含,
共6个基本事件,
从而第2组抽到2人的概率
20.(12分)(1)证明:如图,连接交于点,则为的中点,
的中点,,
平面,平面,平面
.
(2)证明:为正三角形,为的中点,
,平面,,
平面,平面且,
平面,
平面,平面平面
.
(3)平面平面,且交线为,
在平面内,作,则平面
,
,即为直线与平面所成角,
在中,,
,
直线与平面所成角的正弦值为.
21.(12分)(1)由题知的中点,半径.
所以圆的方程为.
(2)由题意可知直线的斜率存在,设直线的方程为,
则圆心到直线的距离,
由题知弦心距为,所以;
解方程得:或
所以直线的方程为或.
22.(12分)(1)因为的解集为,,
所以方程的两根为、,
故,解得,
经检验:当、时,不等式的解集为.
(2)当时,,
对于任意的实数,都有,
即对于任意的实数,都有,
令,
当时,恒成立;
当时,函数是增函数,即,解得;
当时,函数是减函数,即,解得,
综上所述,,的取值范围为.
同课章节目录
