云南省景东一高2021-2022学年高一上学期9月月考数学试题(Word版含答案)
文档属性
| 名称 | 云南省景东一高2021-2022学年高一上学期9月月考数学试题(Word版含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 456.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-18 17:01:12 | ||
图片预览



文档简介
景东一高2021-2022学年高一上学期9月月考
数学试卷
一、单选题
1.点P(4,-2)与圆x2+y2=4上任一点连线的中点轨迹方程是(????)
A.?(x-2)2+(y+1)2=4??????????B.?(x-2)2+(y+1)2=1??????????C.?(x+4)2+(y-2)2=4??????????D.?(x+2)2+(y-1)2=1
2.有一个正四棱锥,它的底面边长与侧棱长均为,现用一张正方形纸将它完全包住(不能裁剪纸,但可以折叠)那么包装纸最小边长应为(??
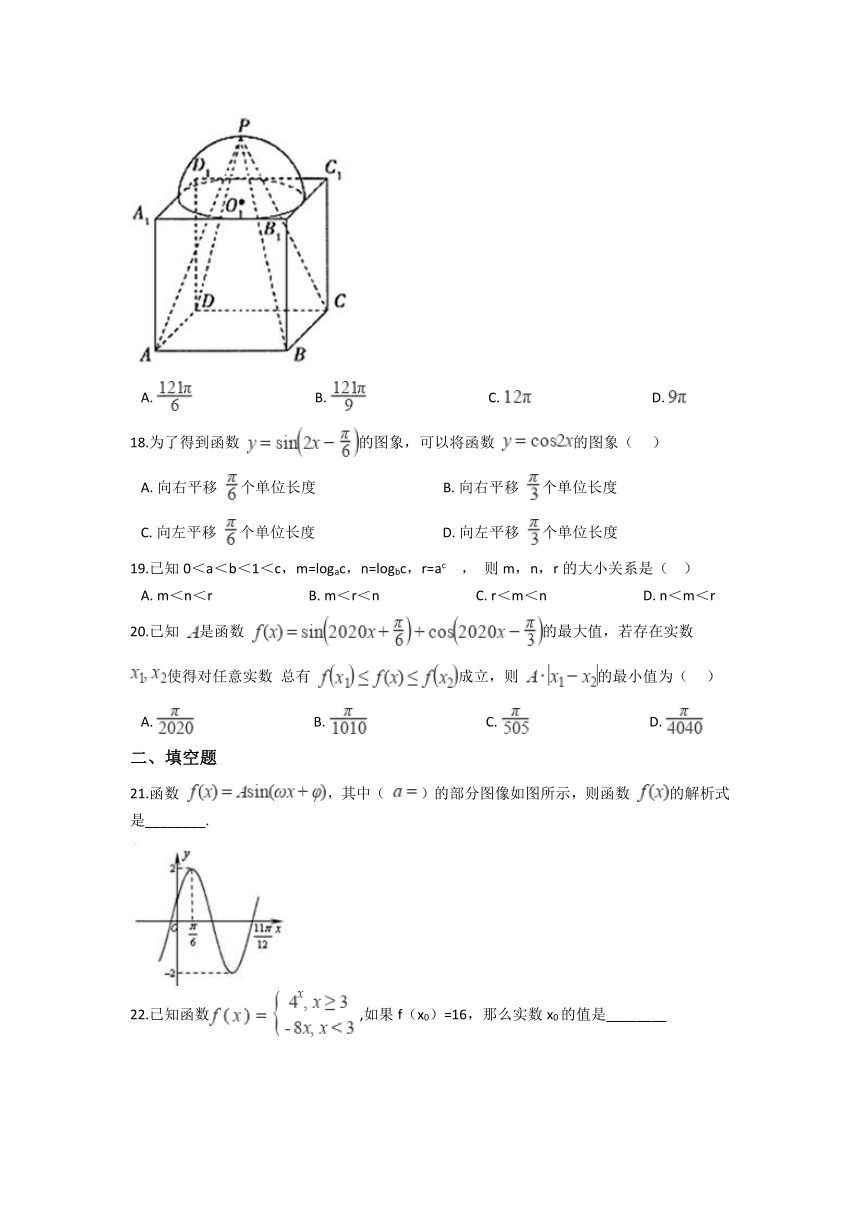
)
A.
B.
C.
D.
3.下列函数中与函数y=﹣3|x|奇偶性相同且在(﹣∞,0)上单调性也相同的是(??
)
A.?y=﹣
????????????????????????????B.?y=log2|x|????????????????????????????C.?y=1﹣x2????????????????????????????D.?y=x3﹣1
4..已知y=f(x)是定义在R上的奇函数,且
为偶函数,对于函数y=f(x)有下列几种描述,其中描述正确的是(?
)
①y=f(x)是周期函数;②x=π是它的一条对称轴
③(﹣π,0)是它图象的一个对称中心;④当
时,它一定取最大值
??????
A.?①②?????????????????????????????????????B.?①③??????????????????????????C.?②④?????????????????????????????????????D.?②③
5.设,
,
,
则的大小关系是(???)
A.????????????????????????????B.????????????????????????????C.????????????????????????????D.?
6.某中学共8个艺术社团,现从中选10名同学组成新春社团慰问小组,其中书法社团需选出3名同学,其他各社团各选出1名同学,现从这10名同学中随机选取3名同学,到社区养老院参加“新春送欢乐”活动(每位同学被选到的可能性相同),则选出的3名同学来自不同社团的概率为( )
A.????????????????????????????????????????B.????????????????????????????????????????C.????????????????????????????????????????D.?
7.函数的单调递增区间是??????????????????????????(?????)
A.???????????????????????????????B.?
C.??????????????????????????????D.?
8.已知
,且函数
在
上有最小值,则a的取值范围为(????
)
A.??????????????????????????????B.??????????????????????????????C.??????????????????????????????D.?
9.设P={x|x<4},Q={x|x2<4},则( )
A.?P?Q?????????????????????????????????B.?Q?P?????????????????????????????????C.?P?CRQ?????????????????????????????????D.?Q?CRP
10.有如下结论:①m∈(P∪Q)?m∈P;②m∈(P∩Q)?m∈(P∪Q);③P?Q?P∪Q=Q;④P∪Q=P?P∩Q=Q.其中正确的个数是(
??)
A.?1个???????????????????????????????????????B.?2个???????????????????????????????????????C.?3个???????????????????????????????????????D.?4个
11..上面图给出的是计算1+2+4+…+22017的值的一个程序框图,则其中判断框内应填入的是(??
)
?
A.?i=2017???????????????????????????B.?i≥2017???????????????????????????C.?i≥2018???????????????????????????D.?i≤2018?
12.定义函数序列:
,
,
,
,
,则函数
的图象与曲线
的交点坐标为(???
)
A.???????????????????????B.???????????????????????C.???????????????????????D.?
13.半径为1的球面上的四点A,B,C,D是一个正四面体的顶点,则这个正四面体的棱长是(?
)
A.???????????????????????????????????????B.???????????????????????????????????????C.???????????????????????????????????????D.?
14.若直角坐标平面内的两点
满足条件:①
都在函数
的图象上;②
关于原点对称.则称点对
是函数
的一对“友好点对”,(点对
与
看作同一对“友好点对”).已知函数
且
,若此函数的“友好点对”有且只有一对,则
的取值范围是(??
)
A.??????????????????B.??????????????????
C.??????????????????D.?
15.在正四棱柱
中,顶点
到对角线
和到平面
的距离分别为
和
,则下列命题中正确的是(
)
A.?若侧棱的长小于底面的变长,则
的取值范围为
??????????
B.?若侧棱的长小于底面的变长,则
的取值范围为
C.?若侧棱的长大于底面的变长,则
的取值范围为
??????????
D.?若侧棱的长大于底面的变长,则
的取值范围为
16.对于向量a,b,e及实数x,y,x1,x2,,
给出下列四个条件:
①且;?????????②
③且唯一;???????
?
??
④
其中能使a与b共线的是???
(???
)
????????
A.?①②?????????????????????????????????????B.?②④?????????????????????????????????????
C.?①③?????????????????????????????????????D.?③④
17.如图为一个正方体
与一个半球
构成的组合体,半球
的底面圆与该正方体的上底面
的四边相切,
与正方形
的中心重合.将此组合体重新置于一个球O中(球O未画出),使该正方体的下底面
的顶点均落在球O的表面上,半球
与球
内切,设切点为P,若正四棱锥
的表面积为
,则球O的表面积为(???
)
A.????????????????????????????????????B.????????????????????????????????????C.????????????????????????????????????D.?
18.为了得到函数
的图象,可以将函数
的图象(???
)
A.?向右平移
个单位长度?????????????????????????????????????B.?向右平移
个单位长度
C.?向左平移
个单位长度?????????????????????????????????????D.?向左平移
个单位长度
19.已知0<a<b<1<c,m=logac,n=logbc,r=ac
,
则m,n,r的大小关系是(??
)
A.?m<n<r????????????????????????????B.?m<r<n????????????????????????????C.?r<m<n????????????????????????????D.?n<m<r
20.已知
是函数
的最大值,若存在实数
使得对任意实数
总有
成立,则
的最小值为(???
)
A.???????????????????????????????????B.???????????????????????????????????C.???????????????????????????????????D.?
二、填空题
21.函数
,其中(
)的部分图像如图所示,则函数
的解析式是________.
22.已知函数,如果f(x0)=16,那么实数x0的值是________?
23.高三年级267位学生参加期末考试,某班37位学生的语文成绩,数学成绩与总成绩在全年级中的排名情况如下图所示,甲、乙、丙为该班三位学生.从这次考试成绩看,
①在甲、乙两人中,其语文成绩名次比其总成绩名次靠前的学生是________?;
②在语文和数学两个科目中,丙同学的成绩名次更靠前的科目是
________??
.
24.空间两点P1(2,3,5),P2(3,1,4)间的距离|P1P2|=________?.
25.已知f(
x–1)=2x+3,且f(m)=17,则m等于________.
26.如图,已知正方形ABCD的边长为1,E在CD延长线上,且DE=CD.动点P从点A出发沿正方形ABCD的边按逆进针方向运动一周回到A点,其中
=λ
+μ
,则下列命题正确的是________.(填上所有正确命题的序号)
①当点P为AD中点时,λ+μ=1;
②λ+μ的最大值为3;
③若y为给定的正数,则一存在向量
和实数x,使
=x
+y
.
27.在三棱锥P﹣ABC中,AB⊥BC,AB=6,
,O为AC的中点,过C作BO的垂线,交BO、AB分别于R、D.若∠DPR=∠CPR,则三棱锥P﹣ABC体积的最大值为________.
28.化简:(-+)+(-)=________
三、解答题
29.已知
,
.
(1)当
时,求
;
(2)若
,求实数a的取值范围.
30.如图,
为线段
的中点,
,
,设
,
,试用
,
表示
,
,
.
31.已知a=
,b=
,求
的值.
32..在△ABC中,已知a、b、c分别是三内角A、B、C所对应的边长,且b2+c2﹣a2=bc
(1).求角A的大小;
(2).若sin2A+sin2B=sin2C,试判断△ABC的形状并求角B的大小.
33.若
,求m的取值范围.
34.已知
均为正实数,求证:
.
35.如图所示,在正方体
中,
分别是
的中点.
(1)求证:平面
平面
;
(2)求证:平面
平面
.
36.设函数
,其中
.
(1)若
的最小正周期为
,求
的单调递增区间.
(2)若函数
的图像的一条对称轴为
,求
的值.
答案解析部分
一、单选题
1.【答案】
B
2.【答案】
B
3.【答案】C
4.【答案】
B
5.【答案】
C
6.【答案】
C
7.【答案】
D
8.【答案】
A
9.【答案】
B
10.【答案】
C
11.【答案】
C
12.【答案】
A
13.【答案】
D
14.【答案】
C
15.【答案】
C
16.【答案】
C
17.【答案】
B
18.【答案】
B
19.【答案】D
20.【答案】
B
二、填空题
21.【答案】
22.【答案】
-2
23.【答案】
乙;数学
24.【答案】
25.【答案】
26.【答案】①②
27.【答案】
3
28.【答案】
三、解答题
29.【答案】
(1)解:
,
当
时,
,故
.
(2)解:(法一)若
,则
∵
,
∴集合
有以下三种情况:
①当
时,
,即
,
∴
或
.
②当
是单元素集时,
,
或
.
若
,则
,不符合题意;若
,则
.
③当
时,
是方程
的两根,
∴
,解得
.
综上可得a的取值范围为
.
(法二)∵
,
又∵
∴
中方程有解,且至少有一解不等于
或
.
∴
,即
.
此时,可分三种情况:
①当
时,
,满足
;
②当
时,
,不合题意;
③当
时,
中有两个元素,若
,则
,故
.
综上,实数a的取值范围为
.
30.【答案】
解:因为
,
,
所以
.
因为
,所以
,
所以
31.【答案】解:a=
,b=
=
32.【答案】
(1)解:在△ABC中,由余弦定理得:a2=b2+c2﹣2bc?cosA,
∴cosA=
,
又∵b2+c2﹣a2=bc,
∴cosA=
,
∵A为三角形内角,
∴A=
;
(2)解:已知等式sin2A+sin2B=sin2C,由正弦定理得a2+b2=c2
,
∴△ABC是以角C为直角的直角三角形,
又A=
,
∴B=
.
33.【答案】
解:原不等式可化为:
,
因为指数函数
在
上单调递减,
所以
,
解得
,
所以
的取值范围为
.
故答案为:
34.【答案】
解:∵
,当且仅当
时等号成立,
∴
,
∴
,
∴
,①
同理
,②
.③
①+②+③,得
,当且仅当
的时等号成立.
35.【答案】
(1)解:连接
,
因为
分别为
的中点,所以
.
因为
,所以
.
又
平面
,
平面
,
所以
平面
,同理
平面
.
因为
,
所以平面
平面
.
(2)解:因为
平面
,
平面
,所以
.
又
,
,
所以
平面
,
又
平面
,所以平面
平面
.
36.【答案】
(1)解:
,
∵
的最小正周期是
,
∴
,
,
∴
,
令
,
,得
,
,∴
的单调增区间为
,
.
(2)解:∵
是
的一条对称轴,
∴
,
,
∴
,
又
,
,
∴
或
.
数学试卷
一、单选题
1.点P(4,-2)与圆x2+y2=4上任一点连线的中点轨迹方程是(????)
A.?(x-2)2+(y+1)2=4??????????B.?(x-2)2+(y+1)2=1??????????C.?(x+4)2+(y-2)2=4??????????D.?(x+2)2+(y-1)2=1
2.有一个正四棱锥,它的底面边长与侧棱长均为,现用一张正方形纸将它完全包住(不能裁剪纸,但可以折叠)那么包装纸最小边长应为(??
)
A.
B.
C.
D.
3.下列函数中与函数y=﹣3|x|奇偶性相同且在(﹣∞,0)上单调性也相同的是(??
)
A.?y=﹣
????????????????????????????B.?y=log2|x|????????????????????????????C.?y=1﹣x2????????????????????????????D.?y=x3﹣1
4..已知y=f(x)是定义在R上的奇函数,且
为偶函数,对于函数y=f(x)有下列几种描述,其中描述正确的是(?
)
①y=f(x)是周期函数;②x=π是它的一条对称轴
③(﹣π,0)是它图象的一个对称中心;④当
时,它一定取最大值
??????
A.?①②?????????????????????????????????????B.?①③??????????????????????????C.?②④?????????????????????????????????????D.?②③
5.设,
,
,
则的大小关系是(???)
A.????????????????????????????B.????????????????????????????C.????????????????????????????D.?
6.某中学共8个艺术社团,现从中选10名同学组成新春社团慰问小组,其中书法社团需选出3名同学,其他各社团各选出1名同学,现从这10名同学中随机选取3名同学,到社区养老院参加“新春送欢乐”活动(每位同学被选到的可能性相同),则选出的3名同学来自不同社团的概率为( )
A.????????????????????????????????????????B.????????????????????????????????????????C.????????????????????????????????????????D.?
7.函数的单调递增区间是??????????????????????????(?????)
A.???????????????????????????????B.?
C.??????????????????????????????D.?
8.已知
,且函数
在
上有最小值,则a的取值范围为(????
)
A.??????????????????????????????B.??????????????????????????????C.??????????????????????????????D.?
9.设P={x|x<4},Q={x|x2<4},则( )
A.?P?Q?????????????????????????????????B.?Q?P?????????????????????????????????C.?P?CRQ?????????????????????????????????D.?Q?CRP
10.有如下结论:①m∈(P∪Q)?m∈P;②m∈(P∩Q)?m∈(P∪Q);③P?Q?P∪Q=Q;④P∪Q=P?P∩Q=Q.其中正确的个数是(
??)
A.?1个???????????????????????????????????????B.?2个???????????????????????????????????????C.?3个???????????????????????????????????????D.?4个
11..上面图给出的是计算1+2+4+…+22017的值的一个程序框图,则其中判断框内应填入的是(??
)
?
A.?i=2017???????????????????????????B.?i≥2017???????????????????????????C.?i≥2018???????????????????????????D.?i≤2018?
12.定义函数序列:
,
,
,
,
,则函数
的图象与曲线
的交点坐标为(???
)
A.???????????????????????B.???????????????????????C.???????????????????????D.?
13.半径为1的球面上的四点A,B,C,D是一个正四面体的顶点,则这个正四面体的棱长是(?
)
A.???????????????????????????????????????B.???????????????????????????????????????C.???????????????????????????????????????D.?
14.若直角坐标平面内的两点
满足条件:①
都在函数
的图象上;②
关于原点对称.则称点对
是函数
的一对“友好点对”,(点对
与
看作同一对“友好点对”).已知函数
且
,若此函数的“友好点对”有且只有一对,则
的取值范围是(??
)
A.??????????????????B.??????????????????
C.??????????????????D.?
15.在正四棱柱
中,顶点
到对角线
和到平面
的距离分别为
和
,则下列命题中正确的是(
)
A.?若侧棱的长小于底面的变长,则
的取值范围为
??????????
B.?若侧棱的长小于底面的变长,则
的取值范围为
C.?若侧棱的长大于底面的变长,则
的取值范围为
??????????
D.?若侧棱的长大于底面的变长,则
的取值范围为
16.对于向量a,b,e及实数x,y,x1,x2,,
给出下列四个条件:
①且;?????????②
③且唯一;???????
?
??
④
其中能使a与b共线的是???
(???
)
????????
A.?①②?????????????????????????????????????B.?②④?????????????????????????????????????
C.?①③?????????????????????????????????????D.?③④
17.如图为一个正方体
与一个半球
构成的组合体,半球
的底面圆与该正方体的上底面
的四边相切,
与正方形
的中心重合.将此组合体重新置于一个球O中(球O未画出),使该正方体的下底面
的顶点均落在球O的表面上,半球
与球
内切,设切点为P,若正四棱锥
的表面积为
,则球O的表面积为(???
)
A.????????????????????????????????????B.????????????????????????????????????C.????????????????????????????????????D.?
18.为了得到函数
的图象,可以将函数
的图象(???
)
A.?向右平移
个单位长度?????????????????????????????????????B.?向右平移
个单位长度
C.?向左平移
个单位长度?????????????????????????????????????D.?向左平移
个单位长度
19.已知0<a<b<1<c,m=logac,n=logbc,r=ac
,
则m,n,r的大小关系是(??
)
A.?m<n<r????????????????????????????B.?m<r<n????????????????????????????C.?r<m<n????????????????????????????D.?n<m<r
20.已知
是函数
的最大值,若存在实数
使得对任意实数
总有
成立,则
的最小值为(???
)
A.???????????????????????????????????B.???????????????????????????????????C.???????????????????????????????????D.?
二、填空题
21.函数
,其中(
)的部分图像如图所示,则函数
的解析式是________.
22.已知函数,如果f(x0)=16,那么实数x0的值是________?
23.高三年级267位学生参加期末考试,某班37位学生的语文成绩,数学成绩与总成绩在全年级中的排名情况如下图所示,甲、乙、丙为该班三位学生.从这次考试成绩看,
①在甲、乙两人中,其语文成绩名次比其总成绩名次靠前的学生是________?;
②在语文和数学两个科目中,丙同学的成绩名次更靠前的科目是
________??
.
24.空间两点P1(2,3,5),P2(3,1,4)间的距离|P1P2|=________?.
25.已知f(
x–1)=2x+3,且f(m)=17,则m等于________.
26.如图,已知正方形ABCD的边长为1,E在CD延长线上,且DE=CD.动点P从点A出发沿正方形ABCD的边按逆进针方向运动一周回到A点,其中
=λ
+μ
,则下列命题正确的是________.(填上所有正确命题的序号)
①当点P为AD中点时,λ+μ=1;
②λ+μ的最大值为3;
③若y为给定的正数,则一存在向量
和实数x,使
=x
+y
.
27.在三棱锥P﹣ABC中,AB⊥BC,AB=6,
,O为AC的中点,过C作BO的垂线,交BO、AB分别于R、D.若∠DPR=∠CPR,则三棱锥P﹣ABC体积的最大值为________.
28.化简:(-+)+(-)=________
三、解答题
29.已知
,
.
(1)当
时,求
;
(2)若
,求实数a的取值范围.
30.如图,
为线段
的中点,
,
,设
,
,试用
,
表示
,
,
.
31.已知a=
,b=
,求
的值.
32..在△ABC中,已知a、b、c分别是三内角A、B、C所对应的边长,且b2+c2﹣a2=bc
(1).求角A的大小;
(2).若sin2A+sin2B=sin2C,试判断△ABC的形状并求角B的大小.
33.若
,求m的取值范围.
34.已知
均为正实数,求证:
.
35.如图所示,在正方体
中,
分别是
的中点.
(1)求证:平面
平面
;
(2)求证:平面
平面
.
36.设函数
,其中
.
(1)若
的最小正周期为
,求
的单调递增区间.
(2)若函数
的图像的一条对称轴为
,求
的值.
答案解析部分
一、单选题
1.【答案】
B
2.【答案】
B
3.【答案】C
4.【答案】
B
5.【答案】
C
6.【答案】
C
7.【答案】
D
8.【答案】
A
9.【答案】
B
10.【答案】
C
11.【答案】
C
12.【答案】
A
13.【答案】
D
14.【答案】
C
15.【答案】
C
16.【答案】
C
17.【答案】
B
18.【答案】
B
19.【答案】D
20.【答案】
B
二、填空题
21.【答案】
22.【答案】
-2
23.【答案】
乙;数学
24.【答案】
25.【答案】
26.【答案】①②
27.【答案】
3
28.【答案】
三、解答题
29.【答案】
(1)解:
,
当
时,
,故
.
(2)解:(法一)若
,则
∵
,
∴集合
有以下三种情况:
①当
时,
,即
,
∴
或
.
②当
是单元素集时,
,
或
.
若
,则
,不符合题意;若
,则
.
③当
时,
是方程
的两根,
∴
,解得
.
综上可得a的取值范围为
.
(法二)∵
,
又∵
∴
中方程有解,且至少有一解不等于
或
.
∴
,即
.
此时,可分三种情况:
①当
时,
,满足
;
②当
时,
,不合题意;
③当
时,
中有两个元素,若
,则
,故
.
综上,实数a的取值范围为
.
30.【答案】
解:因为
,
,
所以
.
因为
,所以
,
所以
31.【答案】解:a=
,b=
=
32.【答案】
(1)解:在△ABC中,由余弦定理得:a2=b2+c2﹣2bc?cosA,
∴cosA=
,
又∵b2+c2﹣a2=bc,
∴cosA=
,
∵A为三角形内角,
∴A=
;
(2)解:已知等式sin2A+sin2B=sin2C,由正弦定理得a2+b2=c2
,
∴△ABC是以角C为直角的直角三角形,
又A=
,
∴B=
.
33.【答案】
解:原不等式可化为:
,
因为指数函数
在
上单调递减,
所以
,
解得
,
所以
的取值范围为
.
故答案为:
34.【答案】
解:∵
,当且仅当
时等号成立,
∴
,
∴
,
∴
,①
同理
,②
.③
①+②+③,得
,当且仅当
的时等号成立.
35.【答案】
(1)解:连接
,
因为
分别为
的中点,所以
.
因为
,所以
.
又
平面
,
平面
,
所以
平面
,同理
平面
.
因为
,
所以平面
平面
.
(2)解:因为
平面
,
平面
,所以
.
又
,
,
所以
平面
,
又
平面
,所以平面
平面
.
36.【答案】
(1)解:
,
∵
的最小正周期是
,
∴
,
,
∴
,
令
,
,得
,
,∴
的单调增区间为
,
.
(2)解:∵
是
的一条对称轴,
∴
,
,
∴
,
又
,
,
∴
或
.
同课章节目录
