冀教版数学九年级上册 25.1比例线段 (共22张)
文档属性
| 名称 | 冀教版数学九年级上册 25.1比例线段 (共22张) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-18 20:03:07 | ||
图片预览







文档简介
(共22张PPT)
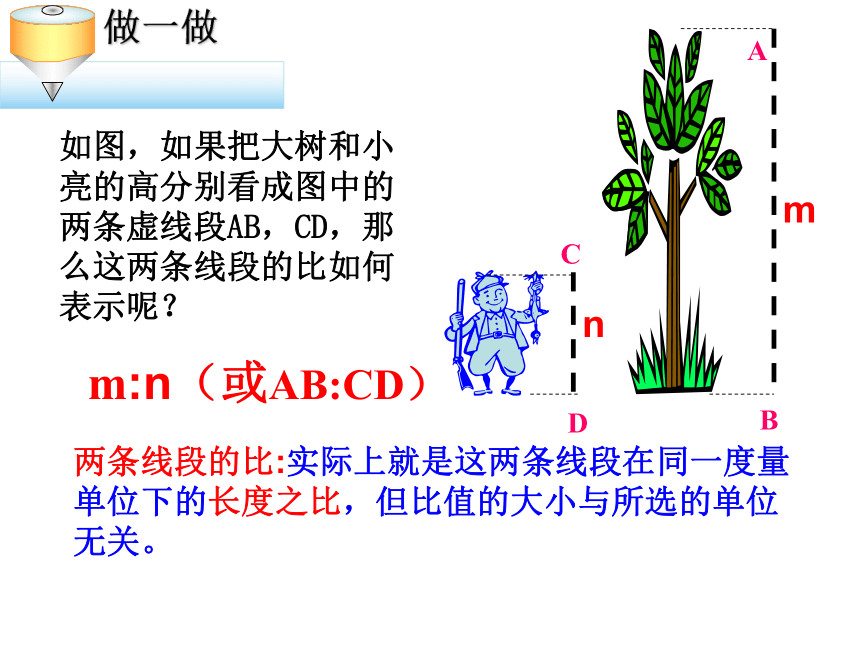
做一做
如图,如果把大树和小亮的高分别看成图中的两条虚线段AB,CD,那么这两条线段的比如何表示呢?
C
D
A
B
m:n(或AB:CD)
两条线段的比:实际上就是这两条线段在同一度量单位下的长度之比,但比值的大小与所选的单位无关。
m
n
线段的比
(1)两条线段的比:如果选用同一个长度单位,量得两
条线段AB,CD的长度分别是m,n,那么就说这两条线段的
比AB:CD=m:n,或写成
。
注意:引入比值k的方法是解决比例问题的一种重要方法,以后经常会用到。
(2)引入比值k的表示方法:如果把
表示成比值k,
那么
,或
AB=k·CD。
注意化单位哦!!!
练习1:已知教室黑板的长
a
=
3.2
m,宽
b
=
120
cm
,求
a:b
解:a
:b
=
320
:120
=
8
:3
或:
练习2:在Rt△ABC中,∠C=90°,
CD是AB边的中线,求CD
:AB
解:CD:AB
=
1
:2
A
B
C
D
练习3:在比例尺是1:6000000的地图上,量得南京到北京的距离是9厘米,南京到北
京的实际距离是
千米。
540
挑战自我:
3.在RtΔABC中
,AC=8,斜边BC=10,则ΔABC中的最短边与最长边的比值是__________
1.画在图纸上的某一零件的长是32mm,如果比例尺是1:20,则该零件的实际长度为
(
)
A.1.6mm
B.
640mm
C.1.5mm
D.608mm
2.在比例尺为1:8000的某学校地图上,矩形运动场的图上尺寸是1cm×2cm,则矩形运动场的实际尺寸是_______________
4.等腰RtΔABC的斜边与直角边之比是_______
B
长160
m,宽80m
3:5
四条线段a、b、c、d中,如果
a与b的比等于c与d的比,即
a/b=c/d,那么这四条线段
a、b、c、d
叫做成比例线段,简称比例线段.
比例线段
记作:
如果a,b,c,d
四个数满足a/b=c/d,
那么ad=bc
吗?反过来,如果ad=bc,那么a/b=c/d
吗?与同伴交流。
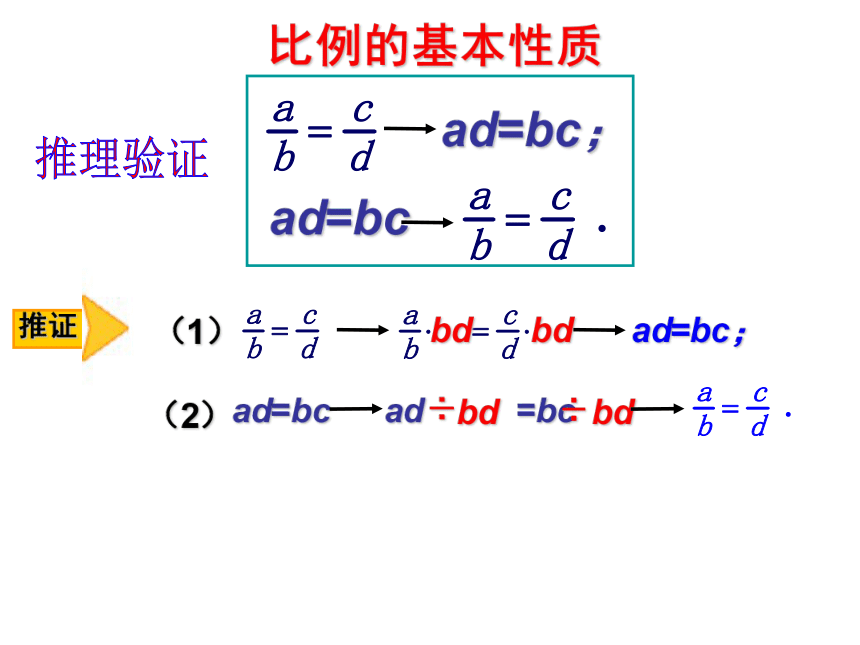
推证
(1)
bd
bd
ad=bc;
(2)
ad=bc
ad
=bc
÷
bd
bd
÷
比例的基本性质
ad=bc
ad=bc;
比例的其它性质
例1
如图,
a
b
c
d
(3)
如果
(1)
已知
(2)
如果
那么
,
这实际上是:比例的合分比性.
用“设k法”,
=k
,
?
?
为什么
成立吗
那么
b
a
f
d
b
e
c
a
=
+
+
+
+
,
f
e
d
c
b
a
=
=
如果
这实际上是:比例的等比性.
B
C
6
比例中项
如果
即:
那么b叫作a和d的比例中项。
做一做
如图,已知线段AB=1,点C是线段AB上一点,
且
(即AC是AB、BC的比例中项)
求线段AC的长.
A
B
.
C
如果点C把线段AB分成两条线段,使AB:AC=AC:BC,那么点C叫作线段AB的黄金分割点。AC是AB和BC的比例中项,AC与AB的比叫作黄金比。
0.618
2
1
5
:
?
-
=
AB
AC
想一想:一条线段上有几个黄金分割点?
查阅
&
欣赏
探索身边的
“黄金分割”
为什么翩翩起舞的芭蕾舞演员要掂起脚?
为什么身材苗条的时装模特还要穿高跟鞋?为什么她们会给人感到和谐、平衡、舒适、美的感觉?
黄金身材比例
黄金分割
与生活
由黄金分割画出的正五角星形,有庄严雄健之美.
古希腊时期的
巴台农神庙
如图是古希腊时期的巴台农神庙,
如果把图中虚线表示的矩形画成下图中的ABCD,以矩形ABCD的宽为边在其内部作正方形AEFD,那么我们可以惊奇的发现
开启
智慧
A
B
C
D
E
F
点E是AB的黄金分割点吗?矩形ABCD的宽与长的比是黄金比吗?
积累就是知识
请用所学知识回答上面的问题
A
B
C
D
E
F
耐人寻味的0.618
读一读
打开地图,你就会发现那些好茶产地大多位于北纬30度左右。特别是红茶中的极品“祁红”,产地在安徽的祁门,也恰好在此纬度上。这不免让人联想起许多与北纬30度有关的地方。奇石异峰,名川秀水的黄山,庐山,九寨沟等等。衔远山,吞长江的中国三大淡水湖也恰好在这黄金分割的纬度上。
蝴蝶身长与双翅展开后的长度之比,
普通树叶的宽与长之比也接近0.618;
节目主持人报幕,绝对不会站在舞台的中央,而总是站在舞台的1/3处,站在舞台上侧近于0.618的位置才是最佳的位置;
生活中用的纸为黄金矩形,这样的长方形让人看起来舒服顺眼,正规裁法得到的纸张,不管其大小,如对于8开、16开、32开等,都仍然是近似的黄金矩形。
数学美的魅力
1
古埃及胡夫金字塔
古希腊巴特农神庙
文明古国埃及的金字塔,形似方锥,大小各异。但这些金字塔底面的边
长与高这比都接近于0.618.
古希腊的一些神庙,在建筑时高和宽也是按黄金比0.618来建立,他们认为这样的长方形看来是较美观;其大理石柱廓,就是根据黄金分割律分割整个神庙的.
数学美的魅力
2
雕塑断臂女神维纳斯的体型完全与黄金比相符,即以人的肚脐为分界点,上身与下身之比,或者说下身与全身之比约是0.618
这样的身体给人的感觉就是非常的匀称,充满着美感.
著名画家达?芬奇的蒙娜丽莎构图就完美的体现了黄金分割在油画艺术上的应用。通过下面两幅图片可以看出来,蒙娜丽莎的头和两肩在整幅画面中都处于完美的体现了黄金分割,使得这幅油画看起来是那么的和谐和完美.
做一做
如图,如果把大树和小亮的高分别看成图中的两条虚线段AB,CD,那么这两条线段的比如何表示呢?
C
D
A
B
m:n(或AB:CD)
两条线段的比:实际上就是这两条线段在同一度量单位下的长度之比,但比值的大小与所选的单位无关。
m
n
线段的比
(1)两条线段的比:如果选用同一个长度单位,量得两
条线段AB,CD的长度分别是m,n,那么就说这两条线段的
比AB:CD=m:n,或写成
。
注意:引入比值k的方法是解决比例问题的一种重要方法,以后经常会用到。
(2)引入比值k的表示方法:如果把
表示成比值k,
那么
,或
AB=k·CD。
注意化单位哦!!!
练习1:已知教室黑板的长
a
=
3.2
m,宽
b
=
120
cm
,求
a:b
解:a
:b
=
320
:120
=
8
:3
或:
练习2:在Rt△ABC中,∠C=90°,
CD是AB边的中线,求CD
:AB
解:CD:AB
=
1
:2
A
B
C
D
练习3:在比例尺是1:6000000的地图上,量得南京到北京的距离是9厘米,南京到北
京的实际距离是
千米。
540
挑战自我:
3.在RtΔABC中
,AC=8,斜边BC=10,则ΔABC中的最短边与最长边的比值是__________
1.画在图纸上的某一零件的长是32mm,如果比例尺是1:20,则该零件的实际长度为
(
)
A.1.6mm
B.
640mm
C.1.5mm
D.608mm
2.在比例尺为1:8000的某学校地图上,矩形运动场的图上尺寸是1cm×2cm,则矩形运动场的实际尺寸是_______________
4.等腰RtΔABC的斜边与直角边之比是_______
B
长160
m,宽80m
3:5
四条线段a、b、c、d中,如果
a与b的比等于c与d的比,即
a/b=c/d,那么这四条线段
a、b、c、d
叫做成比例线段,简称比例线段.
比例线段
记作:
如果a,b,c,d
四个数满足a/b=c/d,
那么ad=bc
吗?反过来,如果ad=bc,那么a/b=c/d
吗?与同伴交流。
推证
(1)
bd
bd
ad=bc;
(2)
ad=bc
ad
=bc
÷
bd
bd
÷
比例的基本性质
ad=bc
ad=bc;
比例的其它性质
例1
如图,
a
b
c
d
(3)
如果
(1)
已知
(2)
如果
那么
,
这实际上是:比例的合分比性.
用“设k法”,
=k
,
?
?
为什么
成立吗
那么
b
a
f
d
b
e
c
a
=
+
+
+
+
,
f
e
d
c
b
a
=
=
如果
这实际上是:比例的等比性.
B
C
6
比例中项
如果
即:
那么b叫作a和d的比例中项。
做一做
如图,已知线段AB=1,点C是线段AB上一点,
且
(即AC是AB、BC的比例中项)
求线段AC的长.
A
B
.
C
如果点C把线段AB分成两条线段,使AB:AC=AC:BC,那么点C叫作线段AB的黄金分割点。AC是AB和BC的比例中项,AC与AB的比叫作黄金比。
0.618
2
1
5
:
?
-
=
AB
AC
想一想:一条线段上有几个黄金分割点?
查阅
&
欣赏
探索身边的
“黄金分割”
为什么翩翩起舞的芭蕾舞演员要掂起脚?
为什么身材苗条的时装模特还要穿高跟鞋?为什么她们会给人感到和谐、平衡、舒适、美的感觉?
黄金身材比例
黄金分割
与生活
由黄金分割画出的正五角星形,有庄严雄健之美.
古希腊时期的
巴台农神庙
如图是古希腊时期的巴台农神庙,
如果把图中虚线表示的矩形画成下图中的ABCD,以矩形ABCD的宽为边在其内部作正方形AEFD,那么我们可以惊奇的发现
开启
智慧
A
B
C
D
E
F
点E是AB的黄金分割点吗?矩形ABCD的宽与长的比是黄金比吗?
积累就是知识
请用所学知识回答上面的问题
A
B
C
D
E
F
耐人寻味的0.618
读一读
打开地图,你就会发现那些好茶产地大多位于北纬30度左右。特别是红茶中的极品“祁红”,产地在安徽的祁门,也恰好在此纬度上。这不免让人联想起许多与北纬30度有关的地方。奇石异峰,名川秀水的黄山,庐山,九寨沟等等。衔远山,吞长江的中国三大淡水湖也恰好在这黄金分割的纬度上。
蝴蝶身长与双翅展开后的长度之比,
普通树叶的宽与长之比也接近0.618;
节目主持人报幕,绝对不会站在舞台的中央,而总是站在舞台的1/3处,站在舞台上侧近于0.618的位置才是最佳的位置;
生活中用的纸为黄金矩形,这样的长方形让人看起来舒服顺眼,正规裁法得到的纸张,不管其大小,如对于8开、16开、32开等,都仍然是近似的黄金矩形。
数学美的魅力
1
古埃及胡夫金字塔
古希腊巴特农神庙
文明古国埃及的金字塔,形似方锥,大小各异。但这些金字塔底面的边
长与高这比都接近于0.618.
古希腊的一些神庙,在建筑时高和宽也是按黄金比0.618来建立,他们认为这样的长方形看来是较美观;其大理石柱廓,就是根据黄金分割律分割整个神庙的.
数学美的魅力
2
雕塑断臂女神维纳斯的体型完全与黄金比相符,即以人的肚脐为分界点,上身与下身之比,或者说下身与全身之比约是0.618
这样的身体给人的感觉就是非常的匀称,充满着美感.
著名画家达?芬奇的蒙娜丽莎构图就完美的体现了黄金分割在油画艺术上的应用。通过下面两幅图片可以看出来,蒙娜丽莎的头和两肩在整幅画面中都处于完美的体现了黄金分割,使得这幅油画看起来是那么的和谐和完美.
同课章节目录
- 第23章 数据分析
- 23.1 平均数与加权平均数
- 23.2 中位数与众数
- 23.3 方差
- 23.4 用样本估计总体
- 第24章 一元二次方程
- 24.1 一元二次方程
- 24.2 解一元二次方程
- 24.3 一元二次方程根与系数的关系
- 24.4 一元二次方程的应用
- 第25章 图形的相似
- 25.1 比例线段
- 25.2 平行线分线段成比例
- 25.3 相似三角形
- 25.4 相似三角形的判定
- 25.5 相似三角形的性质
- 25.6 相似三角形的应用
- 25.7 相似多边形和图形的位似
- 第26章 解直角三角形
- 26.1 锐角三角函数
- 26.2 锐角三角函数的计算
- 26.3 解直角三角形
- 26.4 解直角三角形的应用
- 第27章 反比例函数
- 27.1 反比例函数
- 27.2 反比例函数的图像和性质
- 27.3 反比例函数的应用
- 第28章 圆
- 28.1 圆的概念和性质
- 28.2 过三点的圆
- 28.3 圆心角和圆周角
- 28.4 垂径定理
- 28.5 弧长和扇形面积
