人教版八年级数学上册第11.2三角形有关的角尖子生训练卷(word版、含答案)
文档属性
| 名称 | 人教版八年级数学上册第11.2三角形有关的角尖子生训练卷(word版、含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 128.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-18 21:55:43 | ||
图片预览



文档简介
人教版八年级数学上册-三角形有关的角测验卷(尖子生)
一.选择题(共9小题)
1.如图,已知△ABC中,BD、CE分别是△ABC的角平分线,BD与CE交于点O,如果设∠BAC=n°(0<n<180),那么∠BOE的度数是( )
A.90°﹣n°
B.90°+n°
C.45°+n°
D.180°﹣n°
2.如图,∠BDC=110°,∠C=38°,∠A=35°,∠B的度数是( )
A.43°
B.33°
C.37°
D.47°
3.如图,已知直线a∥b,直角三角形ABC中,∠C=90°,若∠B=58°,那么∠1﹣∠2=( )
A.28°
B.30°
C.32°
D.58°
4.如图,在△ABC中,点D在边AB上,BE∥AC,连接ED.若∠A=56°,∠E=48°,则∠ADE的大小为( )
A.94°
B.98°
C.102°
D.104°
5.将一副三角板按如图所示的方式摆放,则∠1=( )
A.45°
B.60°
C.65°
D.75°
6.如图,已知EF∥GH,Rt△ABC的两个顶点A,B分别在直线GH,EF上,∠C=90°,AC交EF于点D,若BD平分∠ABC,∠BAH=32°.则∠BAC的度数为( )
A.32°
B.26°
C.34°
D.28°
7.将一副三角尺按如图所示的方式摆放,则∠α的大小为( )
A.105°
B.75°
C.65°
D.55°
8.如图,将△ABC纸片沿DE折叠,使点A落在点A'处,且A'B平分∠ABC,A'C平分∠ACB,若∠BA'C=120°,则∠1+∠2的度数为( )
A.90°
B.100°
C.110°
D.120°
9.当三角形中一个内角β是另外一个内角α的时,我们称此三角形为“友好三角形”.如果一个“友好三角形”中有一个内角为54°,那么这个“友好三角形”的“友好角α”的度数为( )
A.108°或27°
B.108°或54°
C.27°或54°或108°
D.54°或84°或108°
二.填空题(共10小题)
10.如图,在△ABC中,AD是BC边上的高,且∠ACB=∠BAD,AE平分∠CAD,交BC于点E.过点E作EF∥AC,分别交AB、AD于点F、G.则下列结论:①∠BAC=90°;②∠AEF=∠BEF;③∠BAE=∠BEA;④∠B=2∠AEF;⑤∠CAD=2∠AEC﹣180°.其中正确的有
.
11.如图,在△ABC中,∠BAC=60°,BD、CE分别平分∠ABC、∠ACB,BD、CE相交于点O,则∠BOC的度数是
.
12.如图,在Rt△ABC中,∠CAB=90°,∠ABC=70°,AF平分∠CAB,交BC于点D.过点C作CE⊥AF于点E,则∠ECD的度数为
.
第10题图
第11题图
第12题图
13.将一副三角板如图放置,其中∠C=30°,∠D=45°,点E在BC边上,M,N分别为AB,DF上的点,G为三角板外一点,连接GM,GN,若∠G=50°,则∠GMB+∠BED+∠DNG=
.
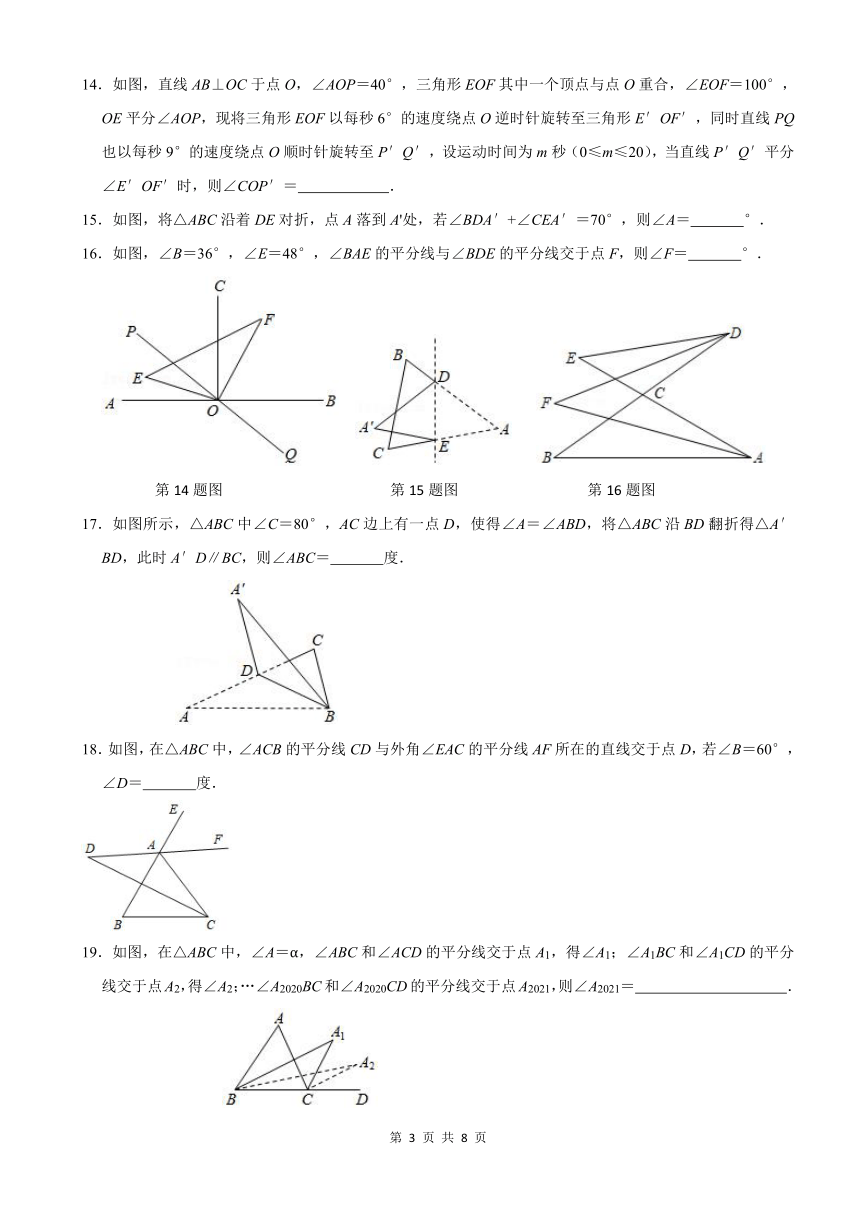
14.如图,直线AB⊥OC于点O,∠AOP=40°,三角形EOF其中一个顶点与点O重合,∠EOF=100°,OE平分∠AOP,现将三角形EOF以每秒6°的速度绕点O逆时针旋转至三角形E′OF′,同时直线PQ也以每秒9°的速度绕点O顺时针旋转至P′Q′,设运动时间为m秒(0≤m≤20),当直线P′Q′平分∠E′OF′时,则∠COP′=
.
15.如图,将△ABC沿着DE对折,点A落到A'处,若∠BDA′+∠CEA′=70°,则∠A=
°.
16.如图,∠B=36°,∠E=48°,∠BAE的平分线与∠BDE的平分线交于点F,则∠F=
°.
第14题图
第15题图
第16题图
如图所示,△ABC中∠C=80°,AC边上有一点D,使得∠A=∠ABD,将△ABC沿BD翻折得△A′BD,此时A′D∥BC,则∠ABC=
度.
18.如图,在△ABC中,∠ACB的平分线CD与外角∠EAC的平分线AF所在的直线交于点D,若∠B=60°,∠D=
度.
19.如图,在△ABC中,∠A=α,∠ABC和∠ACD的平分线交于点A1,得∠A1;∠A1BC和∠A1CD的平分线交于点A2,得∠A2;…∠A2020BC和∠A2020CD的平分线交于点A2021,则∠A2021=
.
三.解答题(共5小题)
20.在△ABC中,∠ABC=2∠A,∠ACB﹣∠ABC=∠A,CE⊥AB,垂足为E,BD是∠ABC的平分线,且交CE于点F.
(1)求∠A,∠ABC,∠ACB;
(2)求∠BFC.
21.如图,在△ABC中,∠ABC和∠ACB的平分线相交于点P.
(1)若∠ABC+∠ACB=130°,求∠BPC的度数.
(2)当∠A为多少度时,∠BPC=3∠A?
22.如图,D是△ABC的AC边上一点,∠A=∠ABD,∠BDC=150°,∠ABC=85°.
求:(1)∠A的度数;
(2)∠C的度数.
解(1)∵∠BDC是△ABD的外角,∠BDC=150°(已知),
∴∠BDC=
+
(
).
又∵∠A=∠ABD(已知),
∴∠A=
度.(等量代换).
(2)∵∠A+∠ABC+∠C=
度(
),
∴∠C=180°﹣∠ABC﹣∠A(等式性质).
又∵∠ABC=85°,
∴∠C=
度.
23.如图,在△ABC中,∠B=40°,∠C=70°,AD是△ABC的角平分线,点E在BD上,点F在CA的延长线上,EF∥AD,求∠F的度数.
24.如图,把△ABC沿EF折叠,使点A落在点D处,
(1)若DE∥AC,试判断∠1与∠2的数量关系,并说明理由;
(2)若∠B+∠C=130°,求∠1+∠2的度数.
25.已知直线AB∥CD.
(1)如图1,写出∠ABE,∠CDE和∠BED之间的数量关系,并说明理由;
(2)如图2,直线MN分别交AB,CD于点F,G,∠AFG与∠CGF的平分线交于点H,则∠FHG的度数为多少?
(3)如图3,在(2)的条件下,∠AFH与∠CGH的平分线交于点I,则∠FIG的度数为
.
【参考答案】
一、选择题。
1-5、ACCDD
6-9、BBDD
填空题。
①③④⑤
11、120°
12、25°
13、55°
14、32°或76°
15、35
16、42
17、75
18、30
19、
三、解答题。
20、解:(1)∵∠ABC=2∠A,∠ACB﹣∠ABC=∠A,∴∠ACB=,
∵∠A+∠ABC+∠ACB=180°,∴∠A+2∠A+=180°,
解得∠A=35°,
∴∠ABC=2∠A=70°,
∠ACB==75°;
(2)∵BD是∠ABC的平分线,∴∠EBF=35°,
∵∠CEB=90°,∴∠BFE=90°﹣35°=55°,
∴∠BFC=180°﹣∠BFE=125°.
21、解:(1)∵PB为∠ABC的平分线,PC为∠ACB的平分线,
∴∠PBC+∠PCB=(∠ABC+∠ACB)=65°.
在△PBC中,∠PBC+∠PCB=65°,
∴∠BPC=180°﹣(∠PBC+∠PCB)=115°.
(2)由(1)可知:∠BPC=180°﹣(∠ABC+∠ACB),
∴∠BPC=180°﹣(180°﹣∠A)=90°+A.
设∠A=α,
∴90°+,解得α=36°,∴∠A=36°.
22、解(1)∵∠BDC是△ABD的外角,∠BDC=150°(已知),
∴∠BDC= ∠A + ∠ABD (
三角形的一个外角等于与它不相邻的两个内角的和 ).
又∵∠A=∠ABD(已知),
∴∠A= 75 度.(等量代换).
(2)∵∠A+∠ABC+∠C= 180 度(
三角形的内角和等于180° ),
∴∠C=180°﹣∠ABC﹣∠A(等式性质).
又∵∠ABC=85°,
∴∠C= 20 度.
23、解:在△ABC中,∠B=40°,∠C=70°,
∴∠BAC=180°﹣∠B﹣∠C=180°﹣40°﹣70°=70°.
∵AD平分∠BAC,∴∠CAD=∠BAC=×70°=35°.
∵EF∥AD,∴∠F=∠CAD=35°.
24、解:(1)∠1=∠2,理由如下:
∵∠D是由∠A翻折得到,∴∠D=∠A,
∵DE∥AC,∴∠1=∠A,∠2=∠D,
∴∠1=∠2.
(2)∵∠A+∠B+∠C=180°,∠A+∠AEF+∠AFE=180°,
∴∠AEF+∠AFE=∠B+∠C=130°,
∵△DEF是△AEF由翻折得到,
∵∠AED=2∠AEF,∠AFD=2∠AFE,∴∠AED+∠AFD=260°,
∵∠1+∠2+∠AED+∠AFD=360°,∴∠1+∠2=100°.
25、解:(1)∠BED=∠ABE+∠CDE,
理由:过点E作EF∥AB,如图所示:
∵AB∥CD,EF∥AB,
∴AB∥CD∥EF,
∴∠ABE=∠BEF,∠CDE=∠DEF,
∵∠BED=∠BEF+∠DEF,
∴∠BED=∠ABE+∠CDE;
(2)解法①:∵∠AFG与∠CGF的平分线交于点H,
∴∠HFG=∠AFG,∠HGF=∠CGF,
∵∠FHG=180°﹣(∠HFG+∠HGF),
∴∠FHG=180°﹣(∠AFG+∠CGF),
∵AB∥CD,
∴∠AFG+∠CGF=180°,
∴∠FHG=180°﹣×180°=90°;
解法②:∵∠AFG与∠CGF的平分线交于点H,
∴∠AFH=12∠AFG,∠CGH=12∠CGF,
由(1)知∠FHG=∠AFH+∠CGH
=(∠AFG+∠CGF)
=×180°
=90°;
(3)解法①:∵∠AFH与∠CGH的平分线交于点I,
∴∠IFH=∠AFH,∠IGH=∠CGH,
∵由(2)得:∠HFG=∠AFH=∠AFG,∠HGF=∠CGH=∠CGF,
∠IFG=∠IFH+HFG,∠IGF=∠IGH+∠HGF,
∴∠IFG=∠AFG,∠IGF=∠CGF,
∵∠FIG=180°﹣∠IFG﹣∠IGF,
∴∠FIG=180°﹣(∠AFG+∠CGF),
∵AB∥CD,
∴∠AFG+∠CGF=180°,
∴∠FIG=180°﹣×180°=45°.
解法②:∵∠AFH与∠CGH的平分线交于点I,
∴∠AFI=∠AFH,∠CGI=∠CGH,
∴∠FIG=(∠AFI+∠CGI)
=(∠AFG+∠CGF)
=×180°
=45°.
故答案为:45°.
一.选择题(共9小题)
1.如图,已知△ABC中,BD、CE分别是△ABC的角平分线,BD与CE交于点O,如果设∠BAC=n°(0<n<180),那么∠BOE的度数是( )
A.90°﹣n°
B.90°+n°
C.45°+n°
D.180°﹣n°
2.如图,∠BDC=110°,∠C=38°,∠A=35°,∠B的度数是( )
A.43°
B.33°
C.37°
D.47°
3.如图,已知直线a∥b,直角三角形ABC中,∠C=90°,若∠B=58°,那么∠1﹣∠2=( )
A.28°
B.30°
C.32°
D.58°
4.如图,在△ABC中,点D在边AB上,BE∥AC,连接ED.若∠A=56°,∠E=48°,则∠ADE的大小为( )
A.94°
B.98°
C.102°
D.104°
5.将一副三角板按如图所示的方式摆放,则∠1=( )
A.45°
B.60°
C.65°
D.75°
6.如图,已知EF∥GH,Rt△ABC的两个顶点A,B分别在直线GH,EF上,∠C=90°,AC交EF于点D,若BD平分∠ABC,∠BAH=32°.则∠BAC的度数为( )
A.32°
B.26°
C.34°
D.28°
7.将一副三角尺按如图所示的方式摆放,则∠α的大小为( )
A.105°
B.75°
C.65°
D.55°
8.如图,将△ABC纸片沿DE折叠,使点A落在点A'处,且A'B平分∠ABC,A'C平分∠ACB,若∠BA'C=120°,则∠1+∠2的度数为( )
A.90°
B.100°
C.110°
D.120°
9.当三角形中一个内角β是另外一个内角α的时,我们称此三角形为“友好三角形”.如果一个“友好三角形”中有一个内角为54°,那么这个“友好三角形”的“友好角α”的度数为( )
A.108°或27°
B.108°或54°
C.27°或54°或108°
D.54°或84°或108°
二.填空题(共10小题)
10.如图,在△ABC中,AD是BC边上的高,且∠ACB=∠BAD,AE平分∠CAD,交BC于点E.过点E作EF∥AC,分别交AB、AD于点F、G.则下列结论:①∠BAC=90°;②∠AEF=∠BEF;③∠BAE=∠BEA;④∠B=2∠AEF;⑤∠CAD=2∠AEC﹣180°.其中正确的有
.
11.如图,在△ABC中,∠BAC=60°,BD、CE分别平分∠ABC、∠ACB,BD、CE相交于点O,则∠BOC的度数是
.
12.如图,在Rt△ABC中,∠CAB=90°,∠ABC=70°,AF平分∠CAB,交BC于点D.过点C作CE⊥AF于点E,则∠ECD的度数为
.
第10题图
第11题图
第12题图
13.将一副三角板如图放置,其中∠C=30°,∠D=45°,点E在BC边上,M,N分别为AB,DF上的点,G为三角板外一点,连接GM,GN,若∠G=50°,则∠GMB+∠BED+∠DNG=
.
14.如图,直线AB⊥OC于点O,∠AOP=40°,三角形EOF其中一个顶点与点O重合,∠EOF=100°,OE平分∠AOP,现将三角形EOF以每秒6°的速度绕点O逆时针旋转至三角形E′OF′,同时直线PQ也以每秒9°的速度绕点O顺时针旋转至P′Q′,设运动时间为m秒(0≤m≤20),当直线P′Q′平分∠E′OF′时,则∠COP′=
.
15.如图,将△ABC沿着DE对折,点A落到A'处,若∠BDA′+∠CEA′=70°,则∠A=
°.
16.如图,∠B=36°,∠E=48°,∠BAE的平分线与∠BDE的平分线交于点F,则∠F=
°.
第14题图
第15题图
第16题图
如图所示,△ABC中∠C=80°,AC边上有一点D,使得∠A=∠ABD,将△ABC沿BD翻折得△A′BD,此时A′D∥BC,则∠ABC=
度.
18.如图,在△ABC中,∠ACB的平分线CD与外角∠EAC的平分线AF所在的直线交于点D,若∠B=60°,∠D=
度.
19.如图,在△ABC中,∠A=α,∠ABC和∠ACD的平分线交于点A1,得∠A1;∠A1BC和∠A1CD的平分线交于点A2,得∠A2;…∠A2020BC和∠A2020CD的平分线交于点A2021,则∠A2021=
.
三.解答题(共5小题)
20.在△ABC中,∠ABC=2∠A,∠ACB﹣∠ABC=∠A,CE⊥AB,垂足为E,BD是∠ABC的平分线,且交CE于点F.
(1)求∠A,∠ABC,∠ACB;
(2)求∠BFC.
21.如图,在△ABC中,∠ABC和∠ACB的平分线相交于点P.
(1)若∠ABC+∠ACB=130°,求∠BPC的度数.
(2)当∠A为多少度时,∠BPC=3∠A?
22.如图,D是△ABC的AC边上一点,∠A=∠ABD,∠BDC=150°,∠ABC=85°.
求:(1)∠A的度数;
(2)∠C的度数.
解(1)∵∠BDC是△ABD的外角,∠BDC=150°(已知),
∴∠BDC=
+
(
).
又∵∠A=∠ABD(已知),
∴∠A=
度.(等量代换).
(2)∵∠A+∠ABC+∠C=
度(
),
∴∠C=180°﹣∠ABC﹣∠A(等式性质).
又∵∠ABC=85°,
∴∠C=
度.
23.如图,在△ABC中,∠B=40°,∠C=70°,AD是△ABC的角平分线,点E在BD上,点F在CA的延长线上,EF∥AD,求∠F的度数.
24.如图,把△ABC沿EF折叠,使点A落在点D处,
(1)若DE∥AC,试判断∠1与∠2的数量关系,并说明理由;
(2)若∠B+∠C=130°,求∠1+∠2的度数.
25.已知直线AB∥CD.
(1)如图1,写出∠ABE,∠CDE和∠BED之间的数量关系,并说明理由;
(2)如图2,直线MN分别交AB,CD于点F,G,∠AFG与∠CGF的平分线交于点H,则∠FHG的度数为多少?
(3)如图3,在(2)的条件下,∠AFH与∠CGH的平分线交于点I,则∠FIG的度数为
.
【参考答案】
一、选择题。
1-5、ACCDD
6-9、BBDD
填空题。
①③④⑤
11、120°
12、25°
13、55°
14、32°或76°
15、35
16、42
17、75
18、30
19、
三、解答题。
20、解:(1)∵∠ABC=2∠A,∠ACB﹣∠ABC=∠A,∴∠ACB=,
∵∠A+∠ABC+∠ACB=180°,∴∠A+2∠A+=180°,
解得∠A=35°,
∴∠ABC=2∠A=70°,
∠ACB==75°;
(2)∵BD是∠ABC的平分线,∴∠EBF=35°,
∵∠CEB=90°,∴∠BFE=90°﹣35°=55°,
∴∠BFC=180°﹣∠BFE=125°.
21、解:(1)∵PB为∠ABC的平分线,PC为∠ACB的平分线,
∴∠PBC+∠PCB=(∠ABC+∠ACB)=65°.
在△PBC中,∠PBC+∠PCB=65°,
∴∠BPC=180°﹣(∠PBC+∠PCB)=115°.
(2)由(1)可知:∠BPC=180°﹣(∠ABC+∠ACB),
∴∠BPC=180°﹣(180°﹣∠A)=90°+A.
设∠A=α,
∴90°+,解得α=36°,∴∠A=36°.
22、解(1)∵∠BDC是△ABD的外角,∠BDC=150°(已知),
∴∠BDC= ∠A + ∠ABD (
三角形的一个外角等于与它不相邻的两个内角的和 ).
又∵∠A=∠ABD(已知),
∴∠A= 75 度.(等量代换).
(2)∵∠A+∠ABC+∠C= 180 度(
三角形的内角和等于180° ),
∴∠C=180°﹣∠ABC﹣∠A(等式性质).
又∵∠ABC=85°,
∴∠C= 20 度.
23、解:在△ABC中,∠B=40°,∠C=70°,
∴∠BAC=180°﹣∠B﹣∠C=180°﹣40°﹣70°=70°.
∵AD平分∠BAC,∴∠CAD=∠BAC=×70°=35°.
∵EF∥AD,∴∠F=∠CAD=35°.
24、解:(1)∠1=∠2,理由如下:
∵∠D是由∠A翻折得到,∴∠D=∠A,
∵DE∥AC,∴∠1=∠A,∠2=∠D,
∴∠1=∠2.
(2)∵∠A+∠B+∠C=180°,∠A+∠AEF+∠AFE=180°,
∴∠AEF+∠AFE=∠B+∠C=130°,
∵△DEF是△AEF由翻折得到,
∵∠AED=2∠AEF,∠AFD=2∠AFE,∴∠AED+∠AFD=260°,
∵∠1+∠2+∠AED+∠AFD=360°,∴∠1+∠2=100°.
25、解:(1)∠BED=∠ABE+∠CDE,
理由:过点E作EF∥AB,如图所示:
∵AB∥CD,EF∥AB,
∴AB∥CD∥EF,
∴∠ABE=∠BEF,∠CDE=∠DEF,
∵∠BED=∠BEF+∠DEF,
∴∠BED=∠ABE+∠CDE;
(2)解法①:∵∠AFG与∠CGF的平分线交于点H,
∴∠HFG=∠AFG,∠HGF=∠CGF,
∵∠FHG=180°﹣(∠HFG+∠HGF),
∴∠FHG=180°﹣(∠AFG+∠CGF),
∵AB∥CD,
∴∠AFG+∠CGF=180°,
∴∠FHG=180°﹣×180°=90°;
解法②:∵∠AFG与∠CGF的平分线交于点H,
∴∠AFH=12∠AFG,∠CGH=12∠CGF,
由(1)知∠FHG=∠AFH+∠CGH
=(∠AFG+∠CGF)
=×180°
=90°;
(3)解法①:∵∠AFH与∠CGH的平分线交于点I,
∴∠IFH=∠AFH,∠IGH=∠CGH,
∵由(2)得:∠HFG=∠AFH=∠AFG,∠HGF=∠CGH=∠CGF,
∠IFG=∠IFH+HFG,∠IGF=∠IGH+∠HGF,
∴∠IFG=∠AFG,∠IGF=∠CGF,
∵∠FIG=180°﹣∠IFG﹣∠IGF,
∴∠FIG=180°﹣(∠AFG+∠CGF),
∵AB∥CD,
∴∠AFG+∠CGF=180°,
∴∠FIG=180°﹣×180°=45°.
解法②:∵∠AFH与∠CGH的平分线交于点I,
∴∠AFI=∠AFH,∠CGI=∠CGH,
∴∠FIG=(∠AFI+∠CGI)
=(∠AFG+∠CGF)
=×180°
=45°.
故答案为:45°.
