吉林省吉林市第二中学2020-2021学年高一下学期期末考试数学试题(Word版含答案)
文档属性
| 名称 | 吉林省吉林市第二中学2020-2021学年高一下学期期末考试数学试题(Word版含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 890.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-18 00:00:00 | ||
图片预览




文档简介
吉林二中2020-2021学年度下学期期末考试
高一数学试卷
第Ⅰ卷
说明:1、本试卷分第I试卷(选择题)和第II卷(非选择题)两部分;
2、满分150分,考试时间
120分钟。
1、单选题(共8题,每题5分,共40分)
1.已知是虚数单位,若,则的共轭复数的虚部为(
)
A.
B.
C.
D.
2.今年6月初,某市采取了鼓励地摊经济的做法,该市各区的地摊的摊位数和食品摊位比例分别如图1、图2所示,现用分层抽样的方法抽取5%的摊位进行调查,则抽取的样本容量与A区被抽取的食品摊位数分别为(
)
A.210,24
B.210,50
C.1500,24
D.1500,50
3.已知圆锥的底面半径为4,高为3,则该圆锥的侧面积为(
)
A.
B.
C.
D.
4.在中,点是线段上靠近的五等分点,,则=(
)
A.
B.
C.
D.
5.已知甲、乙两组数据(已按从小到大顺序排列):甲组:、、、、、;
乙组:、、、、、.
若这两组数据的百分位数、百分位数分别相等,则等于(
)
A.
B.
C.
D.
6.若向量,且与的夹角余弦为,则λ等于( )
A.2
B.
C.或
D.
7.如图所示,为测量山高选择A和另一座山的山顶为测量观测点,从A点测得点的仰角点的仰角以及从点测得,若山高米,则山高等于(
)
A.米
B.米
C.米
D.米
8.若是空间两个不同的平面,是两条不同的直线,则下列命题中正确的是(
)
①若,且,则;
②若,且则;
③若,且,则;
④若,则.
A.①③
B.①④
C.②③
D.③④
二、多选题(共4题,每题5分,共20分,全对得5分,漏选得2
分,错选得0分)
9.从装有个红球和个白球的口袋中任取个球,那么互斥而不对立的事件是(
)
A.恰有个红球与恰有个红球
B.至少有个白球与都是红球
C.恰有个红球与恰有个白球
D.至少有个红球与至少有白球
10.在中,角,,的对边分别为,,,向量,,若,且,则(
)
A.
B.
C.
D.
11.下列利用方向向量、法向量判断线、面位置关系的结论中,正确的是(
)
A.两条不重合直线,的方向向量分别是,,则
B.直线的方向向量,平面的法向量是,则
C.两个不同的平面,的法向量分别是,,则
D.直线的方向向量,平面的法向量是,则
12.如图,正方体的棱长为1,线段上有两个动点,,且,则下列结论中正确的是(
)
A.线段上存在点,使得
B.平面
C.
的面积与的面积相等
D.三棱锥的体积为定值
第II卷
三、填空题(共4题,每题5分,共计20分)
13
中,分别为的对边,,则_____
14.某校甲、乙、丙三名教师每天使用1号录播教室上课的概率分别是0.6,0.6,0.8,这三名教师是否使用1号录播教室相互独立,则某天这三名教师中至少有一人使用1号录播教室上课的概率是______.
15.在《九章算术》中,将四个面都为直角三角形的三棱锥称之为鳖臑.已知在鳖臑中,平面,则该鳖臑的外接球的表面积为_______.
16.已知向量_______,在方向上的投影向量是___________.
四、解答题(共6题,17题10分,18-22每题12分,共计70分)
17.已知z为复数,和均为实数,其中i是虚数单位.
(1)求复数z和;
(2)若在第四象限,求实数的取值范围.
18.已知,,是同一平面内的三个向量,其中=(2,1).
(1)若||=2,且∥,求的坐标;
(2)若,且(+2)⊥(﹣),求与的夹角θ.
19.在①,②,③,,且.这三个条件中任选一个,补充到下面的问题中,并解答.问题:在△ABC中,内角A,B,C的对边分别为a,b,c,且___.
(1)求C;
(2)若c=3,求△ABC面积的最大值.
20.某医院为促进行风建设,拟对医院的服务质量进行量化考核,每个患者就医后可以对医院进行打分,最高分为100分.上个月该医院对100名患者进行了回访调查,将他们按所打分数分成以下几组:第一组,第二组,第三组,第四组,第五组,得到频率分布直方图,如图所示.
(1)
求所打分数不低于60分的患者人数;
(2)
估计所打分数的众数,中位数(精确到0.01),平均数;
(3)该医院在第二?三组患者中按分层抽样的方法抽取6名患者进行深入调查,之后将从这6人中随机抽取2人聘为医院行风监督员,求行风监督员来自不同组的概率.
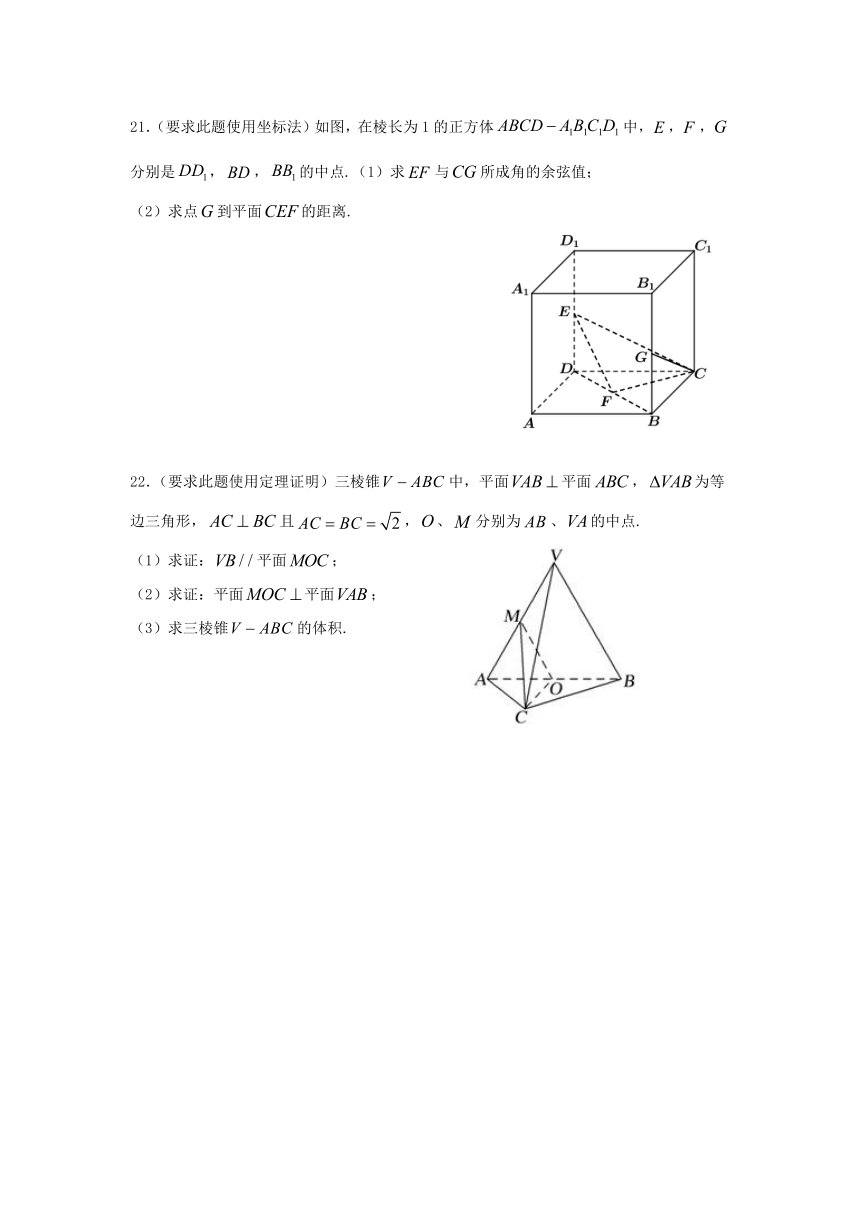
21.(要求此题使用坐标法)如图,在棱长为1的正方体中,,,分别是,,的中点.(1)求与所成角的余弦值;
(2)求点到平面的距离.
22.(要求此题使用定理证明)三棱锥中,平面平面,为等边三角形,且,、分别为、的中点.
(1)求证:平面;
(2)求证:平面平面;
(3)求三棱锥的体积.
吉林二中2020-2021学年度下学期期中考试
高一数学
答案
分值:150
1、
单选题(共8题,每题5分,共40分)
CABA
ADDB
二、多选题(共4题每题5分,共20分全对得5分,漏选得2
分错选得0分)
9.AC
10.ACD
11.AC
12.BD
三、填空题(共4题,每题5分,共计20分)
13.
14.
0.968
15
16.
四、解答题(共6题,17题10分,18-22每题12分,共计70分)
17.
解:(1)设,则,
由为实数,得,则,
由为实数,得,则,
∴,则;
(2)由在第四象限,
得,解得,
故m的取值范围为.
18.【解答】解:(1)∵,,
∴设,且,
∴4λ2+λ2=20,解得λ=±2,
∴或;
(2)∵,且,,
∴=,
∴,
∴,且θ∈[0,π],
∴.
19【详解】
选择条件①:
(1)由正弦定理及,
可得,
因为,所以,
所以;
(2)在中,由余弦定理及,
得,所以,
当且仅当时,等号成立,
则,
所以面积的最大值为.
选择条件②
(1)由正弦定理及,
得,
又,
所以,
因为,所以,
又,所以;
(2)下同选择条件①.
选择条件③:
由,,且,
得,
由余弦定理得,
又,所以;
20【解析】(1)由直方图知,所打分值的频率为
,
人数为(人)
答:所打分数不低于60分的患者的人数为人.
(2)70;
68.57;
65
(3)由直方图知,第二?三组的频率分别为0.1和0.2,
则第二?三组人数分别为10人和20人,
所以根据分层抽样的方法,抽出的6人中,
第二组和第三组的人数之比为1:2,
则第二组有2人,记为;第三组有4人,记为.
从中随机抽取2人的所有情况如下:共15种
其中,两人来自不同组的情况有:共8种
两人来自不同组的概率为
答:行风监督员来自不同组的概率为.
21.(1)设EF与CG所成角为,
,,
则,
所以EF与CG所成角的余弦值为;
(2)
22.三棱锥中,平面平面,为等边三角形,且,、分别为、的中点.
(1)求证:平面;
(2)求证:平面平面;
(3)求三棱锥的体积.
(1)证明:∵、分别为、的中点,∴,
又∵平面,平面,∴平面;
(2)证明:∵,为的中点,∴,
又∵平面平面,平面平面,
且平面,∴平面,又平面,
∴平面平面;
(3)解:在等腰直角三角形中,,
∴,,∴等边三角形的面积,
又∵平面,∴三棱锥的体积,
∴.
高一数学试卷
第Ⅰ卷
说明:1、本试卷分第I试卷(选择题)和第II卷(非选择题)两部分;
2、满分150分,考试时间
120分钟。
1、单选题(共8题,每题5分,共40分)
1.已知是虚数单位,若,则的共轭复数的虚部为(
)
A.
B.
C.
D.
2.今年6月初,某市采取了鼓励地摊经济的做法,该市各区的地摊的摊位数和食品摊位比例分别如图1、图2所示,现用分层抽样的方法抽取5%的摊位进行调查,则抽取的样本容量与A区被抽取的食品摊位数分别为(
)
A.210,24
B.210,50
C.1500,24
D.1500,50
3.已知圆锥的底面半径为4,高为3,则该圆锥的侧面积为(
)
A.
B.
C.
D.
4.在中,点是线段上靠近的五等分点,,则=(
)
A.
B.
C.
D.
5.已知甲、乙两组数据(已按从小到大顺序排列):甲组:、、、、、;
乙组:、、、、、.
若这两组数据的百分位数、百分位数分别相等,则等于(
)
A.
B.
C.
D.
6.若向量,且与的夹角余弦为,则λ等于( )
A.2
B.
C.或
D.
7.如图所示,为测量山高选择A和另一座山的山顶为测量观测点,从A点测得点的仰角点的仰角以及从点测得,若山高米,则山高等于(
)
A.米
B.米
C.米
D.米
8.若是空间两个不同的平面,是两条不同的直线,则下列命题中正确的是(
)
①若,且,则;
②若,且则;
③若,且,则;
④若,则.
A.①③
B.①④
C.②③
D.③④
二、多选题(共4题,每题5分,共20分,全对得5分,漏选得2
分,错选得0分)
9.从装有个红球和个白球的口袋中任取个球,那么互斥而不对立的事件是(
)
A.恰有个红球与恰有个红球
B.至少有个白球与都是红球
C.恰有个红球与恰有个白球
D.至少有个红球与至少有白球
10.在中,角,,的对边分别为,,,向量,,若,且,则(
)
A.
B.
C.
D.
11.下列利用方向向量、法向量判断线、面位置关系的结论中,正确的是(
)
A.两条不重合直线,的方向向量分别是,,则
B.直线的方向向量,平面的法向量是,则
C.两个不同的平面,的法向量分别是,,则
D.直线的方向向量,平面的法向量是,则
12.如图,正方体的棱长为1,线段上有两个动点,,且,则下列结论中正确的是(
)
A.线段上存在点,使得
B.平面
C.
的面积与的面积相等
D.三棱锥的体积为定值
第II卷
三、填空题(共4题,每题5分,共计20分)
13
中,分别为的对边,,则_____
14.某校甲、乙、丙三名教师每天使用1号录播教室上课的概率分别是0.6,0.6,0.8,这三名教师是否使用1号录播教室相互独立,则某天这三名教师中至少有一人使用1号录播教室上课的概率是______.
15.在《九章算术》中,将四个面都为直角三角形的三棱锥称之为鳖臑.已知在鳖臑中,平面,则该鳖臑的外接球的表面积为_______.
16.已知向量_______,在方向上的投影向量是___________.
四、解答题(共6题,17题10分,18-22每题12分,共计70分)
17.已知z为复数,和均为实数,其中i是虚数单位.
(1)求复数z和;
(2)若在第四象限,求实数的取值范围.
18.已知,,是同一平面内的三个向量,其中=(2,1).
(1)若||=2,且∥,求的坐标;
(2)若,且(+2)⊥(﹣),求与的夹角θ.
19.在①,②,③,,且.这三个条件中任选一个,补充到下面的问题中,并解答.问题:在△ABC中,内角A,B,C的对边分别为a,b,c,且___.
(1)求C;
(2)若c=3,求△ABC面积的最大值.
20.某医院为促进行风建设,拟对医院的服务质量进行量化考核,每个患者就医后可以对医院进行打分,最高分为100分.上个月该医院对100名患者进行了回访调查,将他们按所打分数分成以下几组:第一组,第二组,第三组,第四组,第五组,得到频率分布直方图,如图所示.
(1)
求所打分数不低于60分的患者人数;
(2)
估计所打分数的众数,中位数(精确到0.01),平均数;
(3)该医院在第二?三组患者中按分层抽样的方法抽取6名患者进行深入调查,之后将从这6人中随机抽取2人聘为医院行风监督员,求行风监督员来自不同组的概率.
21.(要求此题使用坐标法)如图,在棱长为1的正方体中,,,分别是,,的中点.(1)求与所成角的余弦值;
(2)求点到平面的距离.
22.(要求此题使用定理证明)三棱锥中,平面平面,为等边三角形,且,、分别为、的中点.
(1)求证:平面;
(2)求证:平面平面;
(3)求三棱锥的体积.
吉林二中2020-2021学年度下学期期中考试
高一数学
答案
分值:150
1、
单选题(共8题,每题5分,共40分)
CABA
ADDB
二、多选题(共4题每题5分,共20分全对得5分,漏选得2
分错选得0分)
9.AC
10.ACD
11.AC
12.BD
三、填空题(共4题,每题5分,共计20分)
13.
14.
0.968
15
16.
四、解答题(共6题,17题10分,18-22每题12分,共计70分)
17.
解:(1)设,则,
由为实数,得,则,
由为实数,得,则,
∴,则;
(2)由在第四象限,
得,解得,
故m的取值范围为.
18.【解答】解:(1)∵,,
∴设,且,
∴4λ2+λ2=20,解得λ=±2,
∴或;
(2)∵,且,,
∴=,
∴,
∴,且θ∈[0,π],
∴.
19【详解】
选择条件①:
(1)由正弦定理及,
可得,
因为,所以,
所以;
(2)在中,由余弦定理及,
得,所以,
当且仅当时,等号成立,
则,
所以面积的最大值为.
选择条件②
(1)由正弦定理及,
得,
又,
所以,
因为,所以,
又,所以;
(2)下同选择条件①.
选择条件③:
由,,且,
得,
由余弦定理得,
又,所以;
20【解析】(1)由直方图知,所打分值的频率为
,
人数为(人)
答:所打分数不低于60分的患者的人数为人.
(2)70;
68.57;
65
(3)由直方图知,第二?三组的频率分别为0.1和0.2,
则第二?三组人数分别为10人和20人,
所以根据分层抽样的方法,抽出的6人中,
第二组和第三组的人数之比为1:2,
则第二组有2人,记为;第三组有4人,记为.
从中随机抽取2人的所有情况如下:共15种
其中,两人来自不同组的情况有:共8种
两人来自不同组的概率为
答:行风监督员来自不同组的概率为.
21.(1)设EF与CG所成角为,
,,
则,
所以EF与CG所成角的余弦值为;
(2)
22.三棱锥中,平面平面,为等边三角形,且,、分别为、的中点.
(1)求证:平面;
(2)求证:平面平面;
(3)求三棱锥的体积.
(1)证明:∵、分别为、的中点,∴,
又∵平面,平面,∴平面;
(2)证明:∵,为的中点,∴,
又∵平面平面,平面平面,
且平面,∴平面,又平面,
∴平面平面;
(3)解:在等腰直角三角形中,,
∴,,∴等边三角形的面积,
又∵平面,∴三棱锥的体积,
∴.
同课章节目录
