2021年上海市西南位育高三数学周练试卷(2021.09) (图片版 含答案)
文档属性
| 名称 | 2021年上海市西南位育高三数学周练试卷(2021.09) (图片版 含答案) |  | |
| 格式 | |||
| 文件大小 | 552.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-18 19:35:45 | ||
图片预览

文档简介
西南位育中学高三数学周练试卷01
2021.09
填空题
1.不等式x2+2x-8<0的解集为
2.不等式x+1
≥2的解集为
3.若集合P={y|y=x2},Q={|y=1-2},则P∩Q
4.函数f(x)=,1+√-x2的定义域为
5.已知f(x)是奇函数,当x∈[2,4]时,f(x)=log4(x-1)+x,则f(-3)=
6.若不等式axk6的解集为(-1,),则实数t
7.对数不等式(1+log3x)(a-log3x)>0的解集是(,9),则实数a的值为
8.已知a>0,b>0,且2a+b=1
的最小值为
9.设函数f(x)
则满足∫(x+1)=f(2x)的x的取值范围是
l,x>0
10.已知函数f(x)=21-1|,x∈R,若此函数图像与直线y=t有两个不同的交点
A(m,)、B(n,l),其中m11.已知关于x的不等式(k2-2k-3)x2+(k+1)x+1>0(k∈R)的解集为M,对于任意
n∈N,都有n∈M;对于任意的m∈Z,都有m≠M,则满足条件的k的集合为
12.设f(x)=x2+2ax+b2,其中a,b∈N,x∈R,如果函数y=f(x)与函数
y=f(f(x)都有零点且它们的零点完全相同,则(a,b)为
选择题
若a,b∈R,且ab>0,则下列不等式中恒成立的是
A
a'+b2>2ab
B
a+b>2ab
CI
D
b
14.函数y=f(x)是R上的奇函数,当x<0时,f(x)=2,则当x>0时,f(x)=()
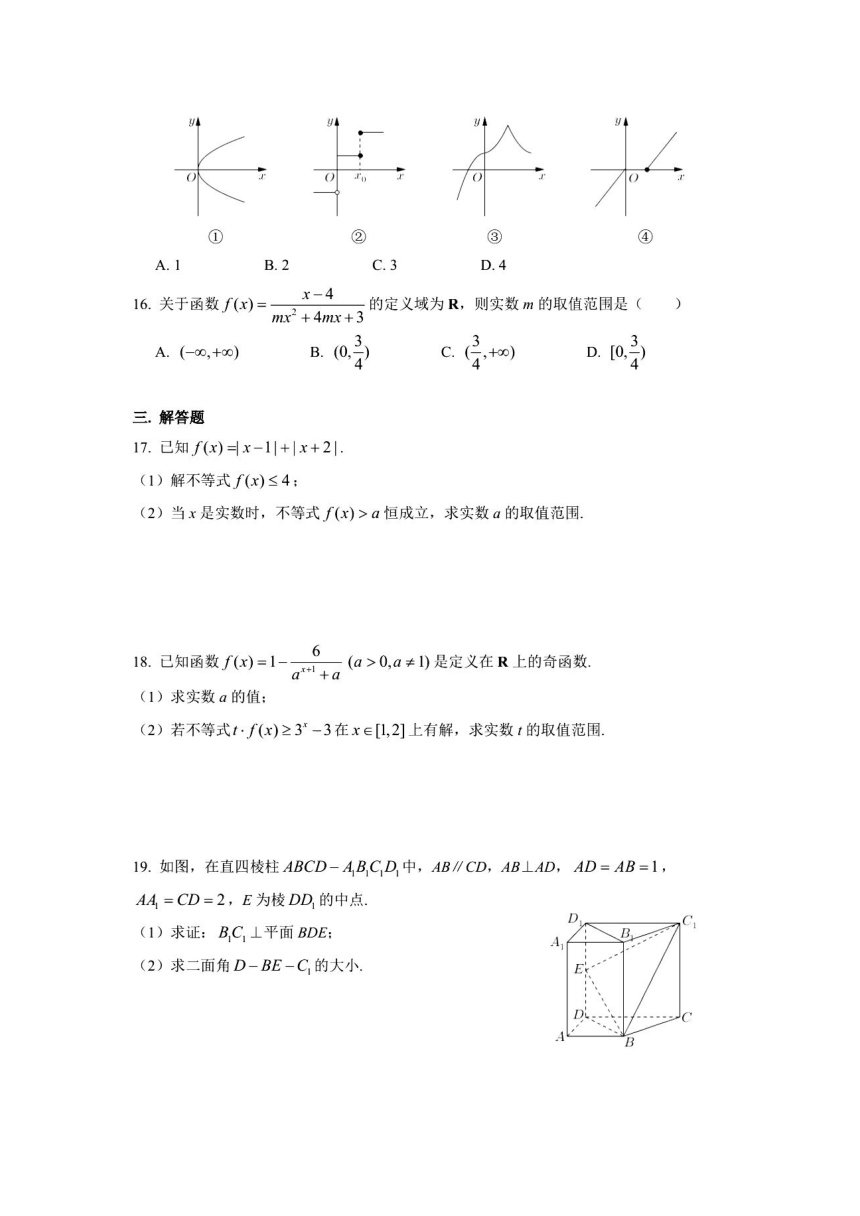
15.下列所给图像是函数图像的个数为()
B.2
(x)
的定义域为R
数m的取值范围是()
mx+4mx+
A.(-∞,+∞
三.解答题
17.已知f(x)=x-1|+|x+2
(1)解不等式f(x)≤4
(2)当x是实数时,不等式∫(x)>a恒成立,求实数a的取值范围
已知函数f(x)=1-6
(a>0,a≠1)是定义在R上的奇函数
(1)求实数a的值:
(2)若不等式1·f(x)≥3-3在x∈[1,2]上有解,求实数t的取值范围
19.如图,在直四棱柱ABCD-ABCD中,AB∥CD,AB⊥AD,AD=AB
A=CD=2,E为棱DD的中点
(1)求证:BC1⊥平面BDE
(2)求二面角D-BE-C1的大小
20.近年来,某企业每年消耗电费约24万元,为了节能减排,决定安装一个可使用15年
的太阳能供电设备接入本企业电网,安装这种供电设备的工本费(单位:万元)与太阳能
电池板的面积(单位:平方米)成正比,比例系数约为0.5,为了保证正常用电,安装后
釆用太阳能和电能互补供电的模式,假设在此模式下,安装后该企业每年消耗的淀粉C
(单位:万元)与安装的这种太阳能电池板的面积x(单位:平方米)之间的函数关系是
C(r)
x≥0,k为常数),记F为该村安装这种太阳能供电设备的费用与
村15年共将消耗的电费之和
)试解释C(O)的实际意义,并建立F关于x的函数关系式
(2)当x为多少平方米时,F取得最小值?最小值是多少万元?
21.已知函数f(x)=2x+b,g(x)=x2+bx+c(b、c∈R),对任意的x∈R恒有
f(x)≤g(x)成立
(1)求证:g(x)>0恒成立
2)设b=0时,记()=8(x)
(x∈[2,+∞)),求函数h(x)的值域
(3)若对满足条件的任意实数b、c,不等式g(c)-g(b)≤M(c2-b2)恒成立
求M的最小值
2021.09
填空题
1.不等式x2+2x-8<0的解集为
2.不等式x+1
≥2的解集为
3.若集合P={y|y=x2},Q={|y=1-2},则P∩Q
4.函数f(x)=,1+√-x2的定义域为
5.已知f(x)是奇函数,当x∈[2,4]时,f(x)=log4(x-1)+x,则f(-3)=
6.若不等式axk6的解集为(-1,),则实数t
7.对数不等式(1+log3x)(a-log3x)>0的解集是(,9),则实数a的值为
8.已知a>0,b>0,且2a+b=1
的最小值为
9.设函数f(x)
则满足∫(x+1)=f(2x)的x的取值范围是
l,x>0
10.已知函数f(x)=21-1|,x∈R,若此函数图像与直线y=t有两个不同的交点
A(m,)、B(n,l),其中m
n∈N,都有n∈M;对于任意的m∈Z,都有m≠M,则满足条件的k的集合为
12.设f(x)=x2+2ax+b2,其中a,b∈N,x∈R,如果函数y=f(x)与函数
y=f(f(x)都有零点且它们的零点完全相同,则(a,b)为
选择题
若a,b∈R,且ab>0,则下列不等式中恒成立的是
A
a'+b2>2ab
B
a+b>2ab
CI
D
b
14.函数y=f(x)是R上的奇函数,当x<0时,f(x)=2,则当x>0时,f(x)=()
15.下列所给图像是函数图像的个数为()
B.2
(x)
的定义域为R
数m的取值范围是()
mx+4mx+
A.(-∞,+∞
三.解答题
17.已知f(x)=x-1|+|x+2
(1)解不等式f(x)≤4
(2)当x是实数时,不等式∫(x)>a恒成立,求实数a的取值范围
已知函数f(x)=1-6
(a>0,a≠1)是定义在R上的奇函数
(1)求实数a的值:
(2)若不等式1·f(x)≥3-3在x∈[1,2]上有解,求实数t的取值范围
19.如图,在直四棱柱ABCD-ABCD中,AB∥CD,AB⊥AD,AD=AB
A=CD=2,E为棱DD的中点
(1)求证:BC1⊥平面BDE
(2)求二面角D-BE-C1的大小
20.近年来,某企业每年消耗电费约24万元,为了节能减排,决定安装一个可使用15年
的太阳能供电设备接入本企业电网,安装这种供电设备的工本费(单位:万元)与太阳能
电池板的面积(单位:平方米)成正比,比例系数约为0.5,为了保证正常用电,安装后
釆用太阳能和电能互补供电的模式,假设在此模式下,安装后该企业每年消耗的淀粉C
(单位:万元)与安装的这种太阳能电池板的面积x(单位:平方米)之间的函数关系是
C(r)
x≥0,k为常数),记F为该村安装这种太阳能供电设备的费用与
村15年共将消耗的电费之和
)试解释C(O)的实际意义,并建立F关于x的函数关系式
(2)当x为多少平方米时,F取得最小值?最小值是多少万元?
21.已知函数f(x)=2x+b,g(x)=x2+bx+c(b、c∈R),对任意的x∈R恒有
f(x)≤g(x)成立
(1)求证:g(x)>0恒成立
2)设b=0时,记()=8(x)
(x∈[2,+∞)),求函数h(x)的值域
(3)若对满足条件的任意实数b、c,不等式g(c)-g(b)≤M(c2-b2)恒成立
求M的最小值
同课章节目录
