北师大版2021--2022九年级(上)数学第二单元《一元二次方程》质量检测试卷B(含解析)
文档属性
| 名称 | 北师大版2021--2022九年级(上)数学第二单元《一元二次方程》质量检测试卷B(含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 963.6KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-19 17:49:15 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
北师大版2021-2022学年九年级(上)第二章一元二次方程检测试卷B
(时间120分钟,满分120分)
一、选择题(共12小题;每小题3分,共36分)
1.
一元二次方程
的根的个数是
A.
B.
C.
D.
2.
要组织一次篮球联赛,赛制为单循环形式,每两队之间都赛一场,计划安排
场比赛.设比赛组织者应邀请
个队参赛,则
满足的关系式为
A.
B.
C.
D.
3.
一个两位数,个位上的数字比十位上的数字小
,且个位上的数字与十位上的数字的平方和比这个两位数小
.设这个两位数的个位上的数字为
,则所列方程为
A.
B.
C.
D.
4.
一元二次方程
的解是
A.
B.
C.
,
D.
,
5.
下列说法正确的是
A.
不是无理方程
B.
不是无理方程
C.
是分式方程
D.
是无理方程
6.
某商品的进价为每件
元,当售价为每件
元时,每星期可卖出
件;现需降价处理,且经市场调查:每降价
元,每星期可多卖出
件.现在要使一个星期的利润为
元,设每件商品应降价
元,则可列方程为
A.
B.
C.
D.
7.
下列方程中有两个实数根的是
A.
B.
C.
D.
8.
下列方程中,一元二次方程有
①
;
②
;
③
;
④
;
⑤
;
⑥
;
⑦
;
⑧
.
A.
个
B.
个
C.
个
D.
个
9.
将一块正方形铁皮的四角各剪去一个边长为
的小正方形,做成一个无盖的盒子,已知盒子的容积是
,则原铁皮的边长为
A.
B.
C.
D.
10.
若关于
的方程
的根是整数,则满足条件的整数
的个数为
A.
个
B.
个
C.
个
D.
个
11.
下列选项是用配方法解一元二次方程
的过程,其中配方正确的是
A.
B.
C.
D.
12.
新能源汽车节能、环保,越来越受消费者喜爱,各种品牌相继投放市场,我国新能源汽车近几年销量全球第一,
年销量为
万辆,销量逐年增加,到
年销量为
万辆.设年平均增长率为
,可列方程为
A.
B.
C.
D.
二、填空题(共6小题;每小题4分,共24分)
13.
已知
,
是一元二次方程
的两个根,则
?,
?.
14.
在实数范围内定义一种新运算,规定:,则方程
的解为
?.
15.
已知方程
和
有共同的根
,则
?,
?.
16.
若
,则
的值为
?.
17.
关于
的方程
中有整数解,
为非负整数,写出
个符合条件的
的取值可以是
?.
18.
关于
的方程
的根是
,(,,,
均为常数,),则方程
的根是
?.
三、解答题(共7小题;共60分)
19.(8分)
解方程:.
20.
(8分)解方程:.
21.
(8分)某校举办“创建全国文明城市”知识竞赛,计划购买甲、乙两种奖品共
件.其中甲种奖品每件
元,乙种奖品每件
元.如果购买甲、乙两种奖品共花费
元,那么这两种奖品分别购买了多少件?
22.
(8分)阅读材料:
例:解方程
.
解:令
,原方程化为
.
因式分解,得
.
于是得
,或
,
,.
当
时,;
当
时,无实数根.
原方程的解是
,.
根据上述方法解方程:.
23.
(10分)某种品牌的手机经过
,
月份连续两次降价,每部售价由
元降到了
元.若每次降价的百分率相同.
(1)求每次降价的百分率;
(2)若
月份继续保持相同的百分率降价,则这种品牌的手机售价为多少元?
24.
(10分)请阅读下列材料:
问题:已知方程
,求一个一元二次方程,使它的根分别是已知方程根的
倍.
解:设所求方程的根为
,则
,
所以
.
把
代入已知方程,得
.
化简,得
.故所求方程为
.
这种利用方程根的代换求新方程的方法,我们称为“换根法”.
(1)已知方程
,求一个一元二次方程,使它的根分别是已知方程根的
倍,则所求方程为
?;
(2)已知关于
的一元二次方程
有两个不等于零的实数根,求一个一元二次方程,使它的根分别是已知方程根的倒数;
(3)已知关于
的方程
有两个实数根,求一个方程,使它的根分别是已知方程根的平方.
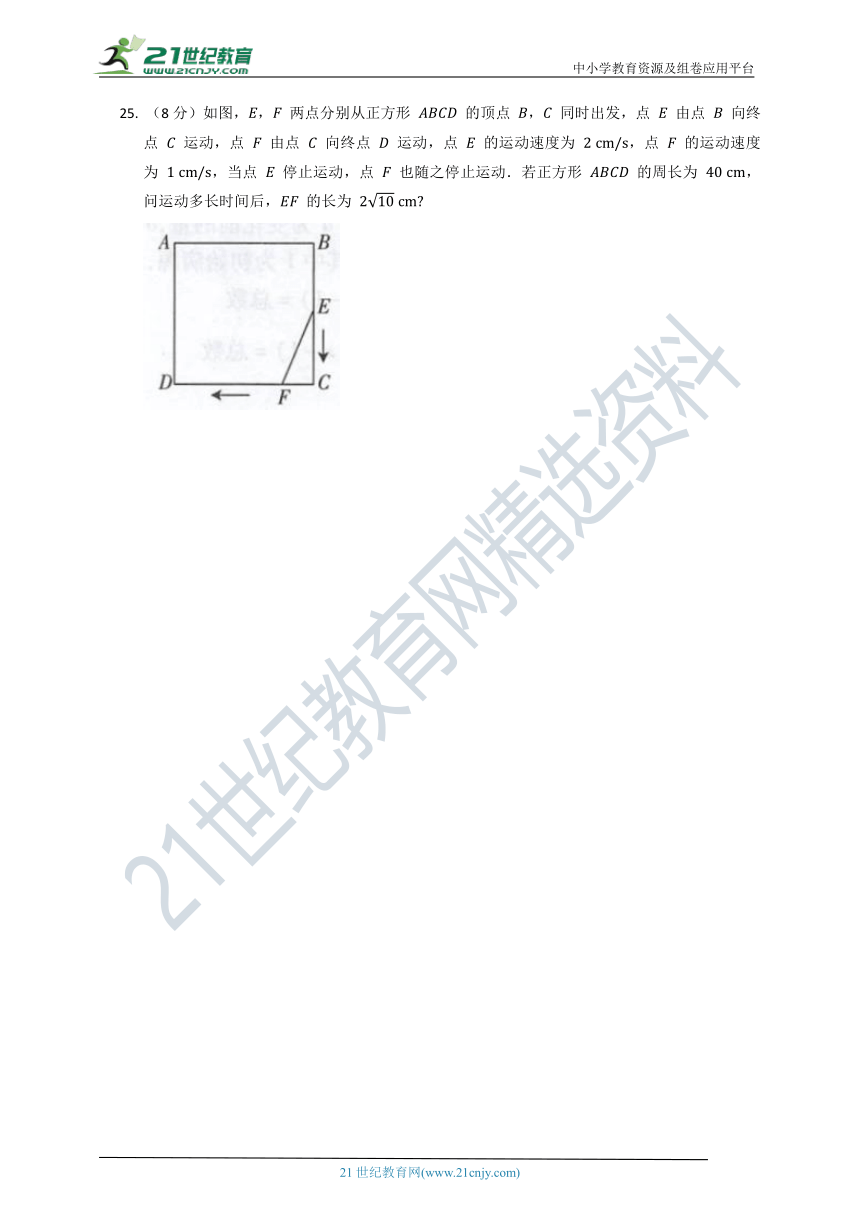
25.
(8分)如图,,
两点分别从正方形
的顶点
,
同时出发,点
由点
向终点
运动,点
由点
向终点
运动,点
的运动速度为
,点
的运动速度为
,当点
停止运动,点
也随之停止运动.若正方形
的周长为
,问运动多长时间后,
的长为
答案
第一部分
1.
A
2.
B
【解析】由题意可得,.
3.
C
【解析】这个两位数的个位上的数字为
,则十位上的数字为
,这个两位数可表示为
.根据题意列方程,得
.
4.
C
【解析】,
或
,
所以
,.
5.
D
6.
C
【解析】根据题意得
.
7.
A
8.
C
【解析】⑦⑧符合一元二次方程的概念,故选C.
9.
D
10.
C
11.
B
【解析】因为
,
所以
,
所以
.
12.
A
【解析】由题意得等量关系:,根据等量关系列出方程为
.
第二部分
13.
,
14.
,
15.
,
16.
【解析】,
,
令
,
,
,
,
.
故答案为
.
17.
或
18.
,
【解析】方程
变形为
,
则可以把它可看作关于
的一元二次方程.
关于
的方程
的根是
,,
在方程
中,
或
,
解得
或
,
即方程
的根是
,.
第三部分
19.
20.
.
21.
设甲种奖品购买了
件,则乙种奖品购买了
件.
根据题意,得
解得
所以
.
答:甲种奖品购买了
件,乙种奖品购买了
件.
22.
令
,原方程可化为
因式分解,得
于是得
当
时,无实数根;
当
时,
原方程的解为
23.
(1)
设每次降价的百分率为
.
由题意,得
解得
,
答:每次降价的百分率为
.
??????(2)
(元).
答:若
月份继续保持相同的百分率降价,则这种品牌的手机售价为
元.
24.
(1)
【解析】设所求方程的根为
,则
,
所以
.
把
代入已知方程,得
,
化简,得
,
故所求方程为
.
??????(2)
设所求方程的根为
,则
,
于是
,
把
代入方程
,得
,
化简,得
.
若
,有
,于是方程
有一个根为
,不符合题意,
.
故所求方程为
.
??????(3)
设所求方程的根为
,则
,
所以
.
①当
时,把
代入已知方程,得
,即
;
②当
时,把
代入已知方程,得
,即
.
故所求方程为
或
.
25.
设运动
后,
的长为
,
由题意,得
,,则
.
在
中,由勾股定理,得
,
即
.
解得
,(舍去).
答:运动
后,
的长为
.
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
21世纪教育网(www.21cnjy.com)
北师大版2021-2022学年九年级(上)第二章一元二次方程检测试卷B
(时间120分钟,满分120分)
一、选择题(共12小题;每小题3分,共36分)
1.
一元二次方程
的根的个数是
A.
B.
C.
D.
2.
要组织一次篮球联赛,赛制为单循环形式,每两队之间都赛一场,计划安排
场比赛.设比赛组织者应邀请
个队参赛,则
满足的关系式为
A.
B.
C.
D.
3.
一个两位数,个位上的数字比十位上的数字小
,且个位上的数字与十位上的数字的平方和比这个两位数小
.设这个两位数的个位上的数字为
,则所列方程为
A.
B.
C.
D.
4.
一元二次方程
的解是
A.
B.
C.
,
D.
,
5.
下列说法正确的是
A.
不是无理方程
B.
不是无理方程
C.
是分式方程
D.
是无理方程
6.
某商品的进价为每件
元,当售价为每件
元时,每星期可卖出
件;现需降价处理,且经市场调查:每降价
元,每星期可多卖出
件.现在要使一个星期的利润为
元,设每件商品应降价
元,则可列方程为
A.
B.
C.
D.
7.
下列方程中有两个实数根的是
A.
B.
C.
D.
8.
下列方程中,一元二次方程有
①
;
②
;
③
;
④
;
⑤
;
⑥
;
⑦
;
⑧
.
A.
个
B.
个
C.
个
D.
个
9.
将一块正方形铁皮的四角各剪去一个边长为
的小正方形,做成一个无盖的盒子,已知盒子的容积是
,则原铁皮的边长为
A.
B.
C.
D.
10.
若关于
的方程
的根是整数,则满足条件的整数
的个数为
A.
个
B.
个
C.
个
D.
个
11.
下列选项是用配方法解一元二次方程
的过程,其中配方正确的是
A.
B.
C.
D.
12.
新能源汽车节能、环保,越来越受消费者喜爱,各种品牌相继投放市场,我国新能源汽车近几年销量全球第一,
年销量为
万辆,销量逐年增加,到
年销量为
万辆.设年平均增长率为
,可列方程为
A.
B.
C.
D.
二、填空题(共6小题;每小题4分,共24分)
13.
已知
,
是一元二次方程
的两个根,则
?,
?.
14.
在实数范围内定义一种新运算,规定:,则方程
的解为
?.
15.
已知方程
和
有共同的根
,则
?,
?.
16.
若
,则
的值为
?.
17.
关于
的方程
中有整数解,
为非负整数,写出
个符合条件的
的取值可以是
?.
18.
关于
的方程
的根是
,(,,,
均为常数,),则方程
的根是
?.
三、解答题(共7小题;共60分)
19.(8分)
解方程:.
20.
(8分)解方程:.
21.
(8分)某校举办“创建全国文明城市”知识竞赛,计划购买甲、乙两种奖品共
件.其中甲种奖品每件
元,乙种奖品每件
元.如果购买甲、乙两种奖品共花费
元,那么这两种奖品分别购买了多少件?
22.
(8分)阅读材料:
例:解方程
.
解:令
,原方程化为
.
因式分解,得
.
于是得
,或
,
,.
当
时,;
当
时,无实数根.
原方程的解是
,.
根据上述方法解方程:.
23.
(10分)某种品牌的手机经过
,
月份连续两次降价,每部售价由
元降到了
元.若每次降价的百分率相同.
(1)求每次降价的百分率;
(2)若
月份继续保持相同的百分率降价,则这种品牌的手机售价为多少元?
24.
(10分)请阅读下列材料:
问题:已知方程
,求一个一元二次方程,使它的根分别是已知方程根的
倍.
解:设所求方程的根为
,则
,
所以
.
把
代入已知方程,得
.
化简,得
.故所求方程为
.
这种利用方程根的代换求新方程的方法,我们称为“换根法”.
(1)已知方程
,求一个一元二次方程,使它的根分别是已知方程根的
倍,则所求方程为
?;
(2)已知关于
的一元二次方程
有两个不等于零的实数根,求一个一元二次方程,使它的根分别是已知方程根的倒数;
(3)已知关于
的方程
有两个实数根,求一个方程,使它的根分别是已知方程根的平方.
25.
(8分)如图,,
两点分别从正方形
的顶点
,
同时出发,点
由点
向终点
运动,点
由点
向终点
运动,点
的运动速度为
,点
的运动速度为
,当点
停止运动,点
也随之停止运动.若正方形
的周长为
,问运动多长时间后,
的长为
答案
第一部分
1.
A
2.
B
【解析】由题意可得,.
3.
C
【解析】这个两位数的个位上的数字为
,则十位上的数字为
,这个两位数可表示为
.根据题意列方程,得
.
4.
C
【解析】,
或
,
所以
,.
5.
D
6.
C
【解析】根据题意得
.
7.
A
8.
C
【解析】⑦⑧符合一元二次方程的概念,故选C.
9.
D
10.
C
11.
B
【解析】因为
,
所以
,
所以
.
12.
A
【解析】由题意得等量关系:,根据等量关系列出方程为
.
第二部分
13.
,
14.
,
15.
,
16.
【解析】,
,
令
,
,
,
,
.
故答案为
.
17.
或
18.
,
【解析】方程
变形为
,
则可以把它可看作关于
的一元二次方程.
关于
的方程
的根是
,,
在方程
中,
或
,
解得
或
,
即方程
的根是
,.
第三部分
19.
20.
.
21.
设甲种奖品购买了
件,则乙种奖品购买了
件.
根据题意,得
解得
所以
.
答:甲种奖品购买了
件,乙种奖品购买了
件.
22.
令
,原方程可化为
因式分解,得
于是得
当
时,无实数根;
当
时,
原方程的解为
23.
(1)
设每次降价的百分率为
.
由题意,得
解得
,
答:每次降价的百分率为
.
??????(2)
(元).
答:若
月份继续保持相同的百分率降价,则这种品牌的手机售价为
元.
24.
(1)
【解析】设所求方程的根为
,则
,
所以
.
把
代入已知方程,得
,
化简,得
,
故所求方程为
.
??????(2)
设所求方程的根为
,则
,
于是
,
把
代入方程
,得
,
化简,得
.
若
,有
,于是方程
有一个根为
,不符合题意,
.
故所求方程为
.
??????(3)
设所求方程的根为
,则
,
所以
.
①当
时,把
代入已知方程,得
,即
;
②当
时,把
代入已知方程,得
,即
.
故所求方程为
或
.
25.
设运动
后,
的长为
,
由题意,得
,,则
.
在
中,由勾股定理,得
,
即
.
解得
,(舍去).
答:运动
后,
的长为
.
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
