五年级上册数学教案 解方程(第1课时) 人教版
文档属性
| 名称 | 五年级上册数学教案 解方程(第1课时) 人教版 |
|
|
| 格式 | zip | ||
| 文件大小 | 563.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-19 06:34:48 | ||
图片预览


文档简介
课程基本信息
课题
解方程(第1课时)
教科书
书名:义务教育教科书数学五年级上册
出版社:人民教育出版社
出版日期:2014
年
3
月第1版
学习目标
学习目标:
1.初步理解“方程的解”与“解方程”的概念,能用等式的性质1解形如?±?=?的简易方程,会检验方程的解。
2.借助直观图示,理解运用等式的性质1将方程变形、求解的过程,感受化归思想。
3.感受知识之间的联系,养成规范书写和自觉检验的习惯,发展自学能力。
学习重点:会解形如?±?=?的简易方程并检验。
学习难点:运用等式的性质1解方程,感受化归思想。
教学过程
时间
教学
环节
主要师生活动
3分钟
一、
回顾引入
(一)观察天平,回顾等式性质
(二)列出方程,明确研究问题
你能根据图中的数量关系列出一个方程吗?
预设:箱子里有个球,箱子外有3个球,合起来一共有9个球。列出的方程是+3=9。
【学习任务一】?的值是多少呢?请你运用所学的知识,尝试解决问题。
10分钟
二、
探索新知
(一)探索交流
方法1:
方法2:
利用三个量之间的关系解决。
方法3:
利用等式的性质1解决。
质疑:为什么要在方程中减3,而不是加3或者乘3呢?
为什么要在方程的两边同时减去3呢?
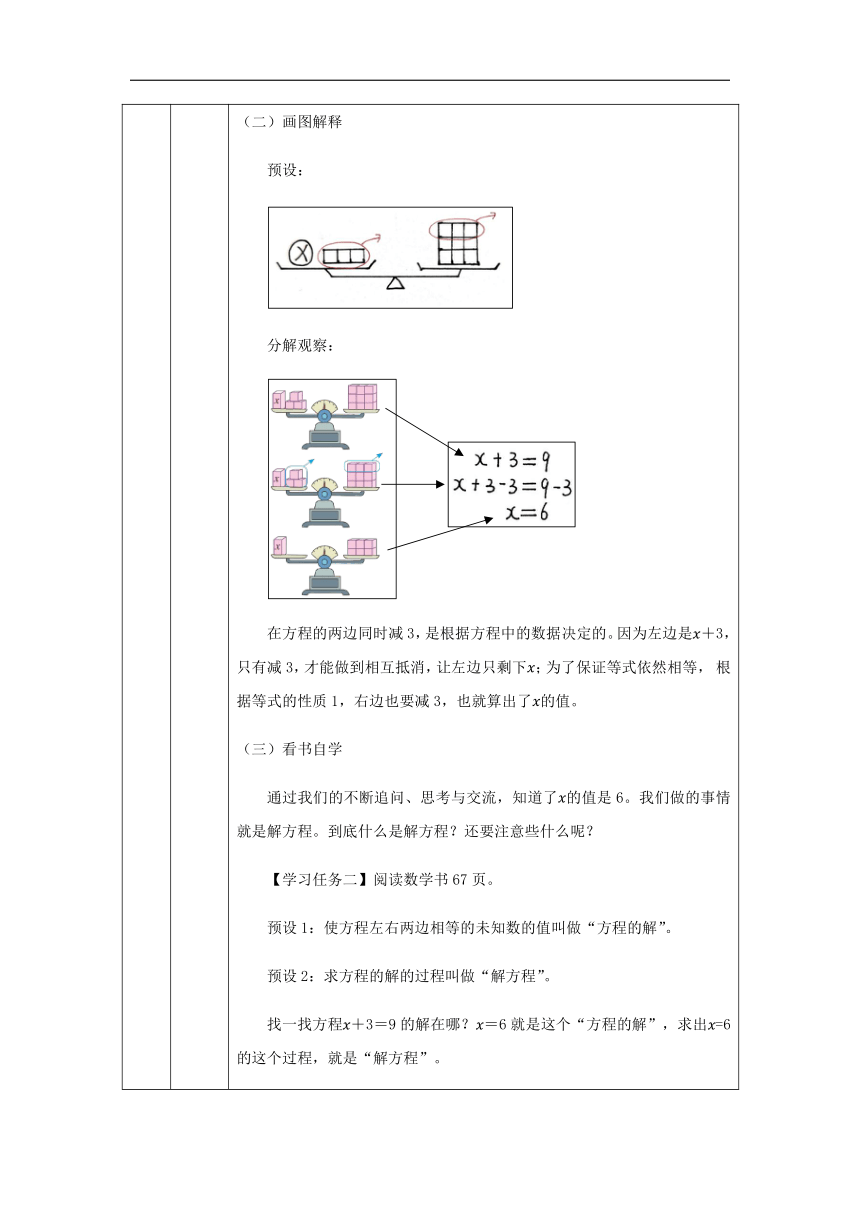
(二)画图解释
预设:
分解观察:
在方程的两边同时减3,是根据方程中的数据决定的。因为左边是+3,只有减3,才能做到相互抵消,让左边只剩下;为了保证等式依然相等,
根据等式的性质1,右边也要减3,也就算出了的值。
(三)看书自学
通过我们的不断追问、思考与交流,知道了的值是6。我们做的事情就是解方程。到底什么是解方程?还要注意些什么呢?
【学习任务二】阅读数学书67页。
预设1:使方程左右两边相等的未知数的值叫做“方程的解”。
预设2:求方程的解的过程叫做“解方程”。
找一找方程?+3=9的解在哪??=6就是这个“方程的解”,求出?=6的这个过程,就是“解方程”。
预设3:解方程的时侯,要先在方程左下角写上“解”,每一步的“等号”要对齐。
预设4:检验方程的解的方法。
同学们,你能说一说怎样检验方程的解吗?
因为方程的解必须使方程的左右两边相等,所以要想知道方程的解对不对,可以把=6代入到方程中算一算,看看方程的左右两边是不是相等。
(四)梳理步骤
1.解方程时先写“解”;
2.利用等式的性质1解方程(在方程左右两边同时加上或者减去相同的数);
3.求出方程的解;
4.注意书写每一步等号对齐,最后检验方程的解。
5分钟
三、
巩固练习
(一)解方程并检验
1.交流计算结果。
(1)?+12=31
(2)100+?=250
(3)??16=20
→
质疑:为什么把=4代入原方程验算,算不出20?
预设1:原方程的左边是?-16,如果方程两边再同时减去16,不能抵消掉原来的减16,也就不能让左边只剩下?了。
预设2:画天平图分析:
这个天平图表示16=20。从左边的里拿走16等于右边的20。要想求出等于几,就要把16拿回来,左边应该加16;要想使天平继续保持平衡,右边也要同时拿来16。就是-16+16=20+16。这样抵消掉16之后,左边就剩下了,右边是36,所以=36。
2.画图分析错误原因。
两边同时减去16的写法,虽然等式依然成立,但方程的左边就变成了-32,没有达到左边只剩下的目的。
3.对比三量关系方法。
用等式的性质来解方程不用考虑三个量之间的关系,只需要关注要抵消谁就可以了。
4.归纳题目共性方法。
解方程的目标就是要让等式的一边只剩下,而保持等式成立的依据是等式的性质。对比三道题目,虽然方程各不相同,有时未知数在方程里表示的是加数,有时未知数在方程里表示的是被减数,但是它们都可以利用等式的性质1,求出方程的解。
(二)解决问题
→
预设1:根据原价-优惠的价钱=现价,列出的方程是?-45=128,解出?=83,原价是83元。
质疑:打折买东西,求出的原价不可能比现价还便宜。代入方程检验,结果不等于128。
在利用等式的性质解方程的时候,一定要特别注意:要在方程的左右两边同时加上或减去同一个数。
预设2:根据原价-现价=优惠的价钱,列出的方程是?-128=45,也能求出方程的解。
1分30秒
五、
回顾总结
回顾这节课的学习,大家有什么收获?
预设:知道了用等式的性质1解方程、解方程的步骤、检验方程的解,画天平图来分析等。
学生提出疑问:等式的性质2也可以用来解方程吗?能够解什么样的方程呢?像3=18、3+4=40这样的方程怎样解呢?
30秒
六、
布置作业
1.数学书第67页做一做第2题。
2.数学书第70页第2题的4道解方程。
课题
解方程(第1课时)
教科书
书名:义务教育教科书数学五年级上册
出版社:人民教育出版社
出版日期:2014
年
3
月第1版
学习目标
学习目标:
1.初步理解“方程的解”与“解方程”的概念,能用等式的性质1解形如?±?=?的简易方程,会检验方程的解。
2.借助直观图示,理解运用等式的性质1将方程变形、求解的过程,感受化归思想。
3.感受知识之间的联系,养成规范书写和自觉检验的习惯,发展自学能力。
学习重点:会解形如?±?=?的简易方程并检验。
学习难点:运用等式的性质1解方程,感受化归思想。
教学过程
时间
教学
环节
主要师生活动
3分钟
一、
回顾引入
(一)观察天平,回顾等式性质
(二)列出方程,明确研究问题
你能根据图中的数量关系列出一个方程吗?
预设:箱子里有个球,箱子外有3个球,合起来一共有9个球。列出的方程是+3=9。
【学习任务一】?的值是多少呢?请你运用所学的知识,尝试解决问题。
10分钟
二、
探索新知
(一)探索交流
方法1:
方法2:
利用三个量之间的关系解决。
方法3:
利用等式的性质1解决。
质疑:为什么要在方程中减3,而不是加3或者乘3呢?
为什么要在方程的两边同时减去3呢?
(二)画图解释
预设:
分解观察:
在方程的两边同时减3,是根据方程中的数据决定的。因为左边是+3,只有减3,才能做到相互抵消,让左边只剩下;为了保证等式依然相等,
根据等式的性质1,右边也要减3,也就算出了的值。
(三)看书自学
通过我们的不断追问、思考与交流,知道了的值是6。我们做的事情就是解方程。到底什么是解方程?还要注意些什么呢?
【学习任务二】阅读数学书67页。
预设1:使方程左右两边相等的未知数的值叫做“方程的解”。
预设2:求方程的解的过程叫做“解方程”。
找一找方程?+3=9的解在哪??=6就是这个“方程的解”,求出?=6的这个过程,就是“解方程”。
预设3:解方程的时侯,要先在方程左下角写上“解”,每一步的“等号”要对齐。
预设4:检验方程的解的方法。
同学们,你能说一说怎样检验方程的解吗?
因为方程的解必须使方程的左右两边相等,所以要想知道方程的解对不对,可以把=6代入到方程中算一算,看看方程的左右两边是不是相等。
(四)梳理步骤
1.解方程时先写“解”;
2.利用等式的性质1解方程(在方程左右两边同时加上或者减去相同的数);
3.求出方程的解;
4.注意书写每一步等号对齐,最后检验方程的解。
5分钟
三、
巩固练习
(一)解方程并检验
1.交流计算结果。
(1)?+12=31
(2)100+?=250
(3)??16=20
→
质疑:为什么把=4代入原方程验算,算不出20?
预设1:原方程的左边是?-16,如果方程两边再同时减去16,不能抵消掉原来的减16,也就不能让左边只剩下?了。
预设2:画天平图分析:
这个天平图表示16=20。从左边的里拿走16等于右边的20。要想求出等于几,就要把16拿回来,左边应该加16;要想使天平继续保持平衡,右边也要同时拿来16。就是-16+16=20+16。这样抵消掉16之后,左边就剩下了,右边是36,所以=36。
2.画图分析错误原因。
两边同时减去16的写法,虽然等式依然成立,但方程的左边就变成了-32,没有达到左边只剩下的目的。
3.对比三量关系方法。
用等式的性质来解方程不用考虑三个量之间的关系,只需要关注要抵消谁就可以了。
4.归纳题目共性方法。
解方程的目标就是要让等式的一边只剩下,而保持等式成立的依据是等式的性质。对比三道题目,虽然方程各不相同,有时未知数在方程里表示的是加数,有时未知数在方程里表示的是被减数,但是它们都可以利用等式的性质1,求出方程的解。
(二)解决问题
→
预设1:根据原价-优惠的价钱=现价,列出的方程是?-45=128,解出?=83,原价是83元。
质疑:打折买东西,求出的原价不可能比现价还便宜。代入方程检验,结果不等于128。
在利用等式的性质解方程的时候,一定要特别注意:要在方程的左右两边同时加上或减去同一个数。
预设2:根据原价-现价=优惠的价钱,列出的方程是?-128=45,也能求出方程的解。
1分30秒
五、
回顾总结
回顾这节课的学习,大家有什么收获?
预设:知道了用等式的性质1解方程、解方程的步骤、检验方程的解,画天平图来分析等。
学生提出疑问:等式的性质2也可以用来解方程吗?能够解什么样的方程呢?像3=18、3+4=40这样的方程怎样解呢?
30秒
六、
布置作业
1.数学书第67页做一做第2题。
2.数学书第70页第2题的4道解方程。
