五年级数学上册表格式教案方程的意义-人教版
文档属性
| 名称 | 五年级数学上册表格式教案方程的意义-人教版 |  | |
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-19 06:57:38 | ||
图片预览

文档简介
课程基本信息
课题
方程的意义
教科书
书名:义务教育教科书数学五年级上册
出版社:人民教育出版社
出版日期:2014年3月第1版
学习目标
学习目标:
1.在具体情境中,初步理解方程的意义,并能根据问题找到等量关系,列出方程。
2.在找等量关系列方程的过程中,发展抽象能力,感悟等价思想和模型思想。
3.感受数学与现实生活的联系,体会方程的应用价值,增强学习数学的兴趣。
学习重点:初步理解方程的意义,并能根据问题找到等量关系,列出方程。
学习难点:初步理解方程的意义。
教学过程
时间
教学
环节
主要师生活动
8分钟
一、
结合
情境,
体会
意义
(一)认识天平,用式子表示天平的状态
1.认识天平,理解原理。
教师组织学生认识天平,引导学生用一个式子表示下图中天平的状态。
预设:50+50=100。
引导学生理解天平平衡表示天平左右两边物体的质量相等。
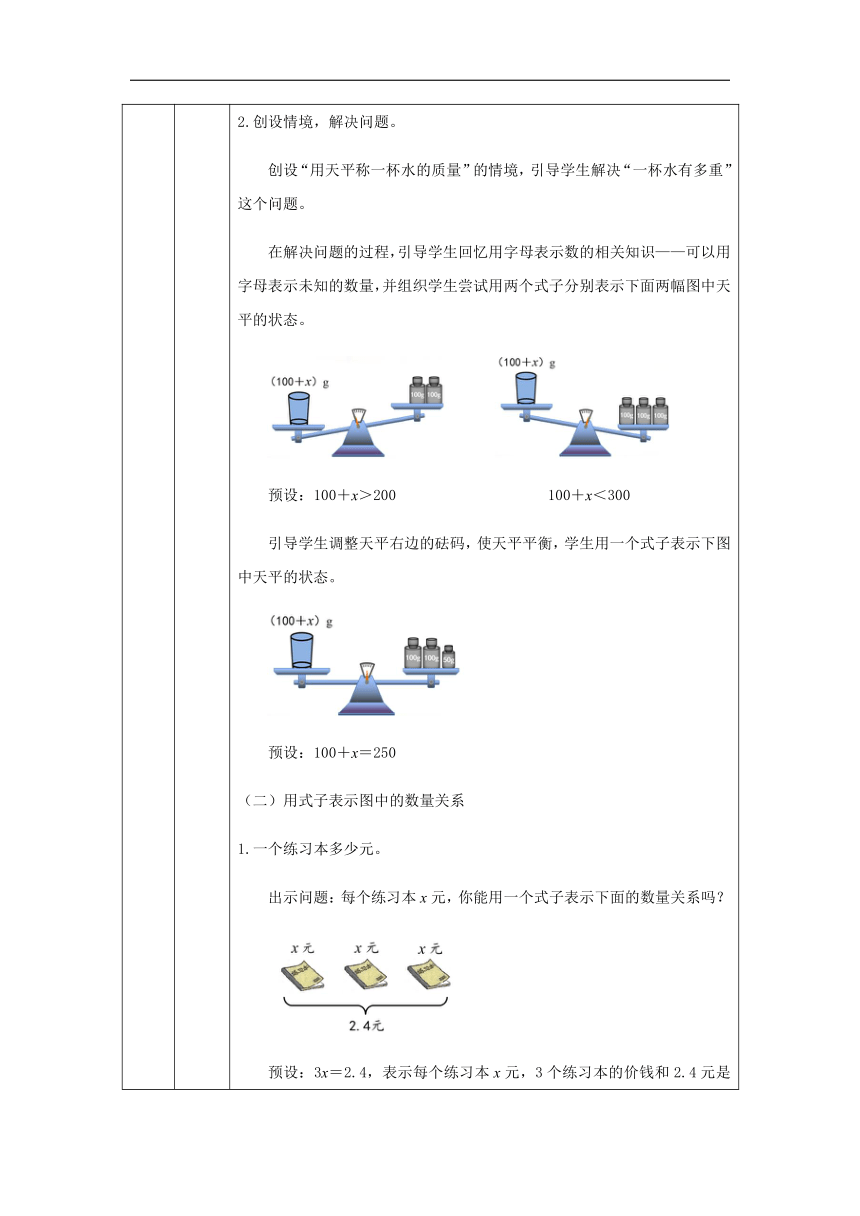
2.创设情境,解决问题。
创设“用天平称一杯水的质量”的情境,引导学生解决“一杯水有多重”这个问题。
在解决问题的过程,引导学生回忆用字母表示数的相关知识——可以用字母表示未知的数量,并组织学生尝试用两个式子分别表示下面两幅图中天平的状态。
预设:100+x>200
100+x<300
引导学生调整天平右边的砝码,使天平平衡,学生用一个式子表示下图中天平的状态。
预设:100+x=250
(二)用式子表示图中的数量关系
1.一个练习本多少元。
出示问题:每个练习本x元,你能用一个式子表示下面的数量关系吗?
预设:3x=2.4,表示每个练习本x元,3个练习本的价钱和2.4元是相等的。
2.一杯果汁多少克。
出示问题:如果每小杯果汁是x
g,你能用一个式子表示下面的数量关系吗?
预设1:一杯果汁x克,3杯果汁就是3x克,还剩(1200-3x)克,还知道剩下的果汁是450克,它们都表示剩下果汁的质量,所以,可以用1200-3x=450表示。
预设2:3x+450=1200,表示的是3小杯果汁的质量加上剩下的450克就等于一大杯果汁的质量1200克。
5分钟
二、
借助
分类,
认识
方程
(一)初步分类,认识等式
引导学生对下面的式子进行分类。
预设:把用等号连接起来的式子分成一类,把剩下的100+x>200和100+x<300分为一类。
借助分类的结果,引导学生认识等式和不等式。
等式
不等式
(二)再次分类,认识方程
引导学生在第一次分类的基础上继续分类。
预设:在这些等式中,有的含有未知数,有的不含有未知数。所以,把50+50=100分为一类,它是不含有未知数的等式;其他的等式分为一类,它们都是含有未知数的等式。
教师揭示方程的意义。像100+x=250、3x=2.4……这样,含有未知数的等式就是方程。
5分钟
三、
练习
巩固,拓展
提升
(一)根据意义,判断方程
下面哪些式子是方程?
35+65=100
x-14>72
y+24
5x+32=47
28<16+14
6(y+2)=42
预设1:5x+32=47和6(y+2)=42是方程。因为,这两个式子既是等式,又含有未知数。
预设2:35+65=100虽然是等式,但不含有未知数;x-14>72
和y+24虽然含有未知数,但不是等式;28<16+14既不是等式,也不含有未知数;所以这几个式子都不是方程。
(二)根据图意,列出方程
用方程表示下面的数量关系。
预设1:第一幅图中,天平左边是2x,右边是50
g,天平平衡了,说明左右两边的质量相等,用方程表示是:2x=50。
预设2:第二幅图中,这条线段由两部分组成,一部分是x,另一部分是73,合起来就是166,用方程表示是:x+73=166。
预设3:第三幅图中,现在车上有24人,有8人上车,就减去8,有5人下车,就加上5,这样才等于原来有x人,也就是24-8+5=x。
预设4:第三幅图中,车上原来有x人,到站后,有5人下车就减去5,有8人上车,就加上8,就等于现在车上的24人,列出的方程就是x-5+8=24。
引导学生对比24-8+5=x和x-5+8=24的不同,体会在列方程时,可以把未知数用x表示,想成已知数,顺着题意想,这样列方程更容易。
1分钟
四、
学生
总结,
汇报
收获
通过本节课的学习,你有什么收获?
预设1:含有未知数的等式就是方程。
预设2:方程就像一架天平,表示了左右两边的相等关系。
预设3:方程是把未知数当成已知数,顺着题意想,找到相等关系,就能列出方程。
1分钟
五、
课后
练习
1.数学书第66页第1题。
2.数学书第66页第3题。
课题
方程的意义
教科书
书名:义务教育教科书数学五年级上册
出版社:人民教育出版社
出版日期:2014年3月第1版
学习目标
学习目标:
1.在具体情境中,初步理解方程的意义,并能根据问题找到等量关系,列出方程。
2.在找等量关系列方程的过程中,发展抽象能力,感悟等价思想和模型思想。
3.感受数学与现实生活的联系,体会方程的应用价值,增强学习数学的兴趣。
学习重点:初步理解方程的意义,并能根据问题找到等量关系,列出方程。
学习难点:初步理解方程的意义。
教学过程
时间
教学
环节
主要师生活动
8分钟
一、
结合
情境,
体会
意义
(一)认识天平,用式子表示天平的状态
1.认识天平,理解原理。
教师组织学生认识天平,引导学生用一个式子表示下图中天平的状态。
预设:50+50=100。
引导学生理解天平平衡表示天平左右两边物体的质量相等。
2.创设情境,解决问题。
创设“用天平称一杯水的质量”的情境,引导学生解决“一杯水有多重”这个问题。
在解决问题的过程,引导学生回忆用字母表示数的相关知识——可以用字母表示未知的数量,并组织学生尝试用两个式子分别表示下面两幅图中天平的状态。
预设:100+x>200
100+x<300
引导学生调整天平右边的砝码,使天平平衡,学生用一个式子表示下图中天平的状态。
预设:100+x=250
(二)用式子表示图中的数量关系
1.一个练习本多少元。
出示问题:每个练习本x元,你能用一个式子表示下面的数量关系吗?
预设:3x=2.4,表示每个练习本x元,3个练习本的价钱和2.4元是相等的。
2.一杯果汁多少克。
出示问题:如果每小杯果汁是x
g,你能用一个式子表示下面的数量关系吗?
预设1:一杯果汁x克,3杯果汁就是3x克,还剩(1200-3x)克,还知道剩下的果汁是450克,它们都表示剩下果汁的质量,所以,可以用1200-3x=450表示。
预设2:3x+450=1200,表示的是3小杯果汁的质量加上剩下的450克就等于一大杯果汁的质量1200克。
5分钟
二、
借助
分类,
认识
方程
(一)初步分类,认识等式
引导学生对下面的式子进行分类。
预设:把用等号连接起来的式子分成一类,把剩下的100+x>200和100+x<300分为一类。
借助分类的结果,引导学生认识等式和不等式。
等式
不等式
(二)再次分类,认识方程
引导学生在第一次分类的基础上继续分类。
预设:在这些等式中,有的含有未知数,有的不含有未知数。所以,把50+50=100分为一类,它是不含有未知数的等式;其他的等式分为一类,它们都是含有未知数的等式。
教师揭示方程的意义。像100+x=250、3x=2.4……这样,含有未知数的等式就是方程。
5分钟
三、
练习
巩固,拓展
提升
(一)根据意义,判断方程
下面哪些式子是方程?
35+65=100
x-14>72
y+24
5x+32=47
28<16+14
6(y+2)=42
预设1:5x+32=47和6(y+2)=42是方程。因为,这两个式子既是等式,又含有未知数。
预设2:35+65=100虽然是等式,但不含有未知数;x-14>72
和y+24虽然含有未知数,但不是等式;28<16+14既不是等式,也不含有未知数;所以这几个式子都不是方程。
(二)根据图意,列出方程
用方程表示下面的数量关系。
预设1:第一幅图中,天平左边是2x,右边是50
g,天平平衡了,说明左右两边的质量相等,用方程表示是:2x=50。
预设2:第二幅图中,这条线段由两部分组成,一部分是x,另一部分是73,合起来就是166,用方程表示是:x+73=166。
预设3:第三幅图中,现在车上有24人,有8人上车,就减去8,有5人下车,就加上5,这样才等于原来有x人,也就是24-8+5=x。
预设4:第三幅图中,车上原来有x人,到站后,有5人下车就减去5,有8人上车,就加上8,就等于现在车上的24人,列出的方程就是x-5+8=24。
引导学生对比24-8+5=x和x-5+8=24的不同,体会在列方程时,可以把未知数用x表示,想成已知数,顺着题意想,这样列方程更容易。
1分钟
四、
学生
总结,
汇报
收获
通过本节课的学习,你有什么收获?
预设1:含有未知数的等式就是方程。
预设2:方程就像一架天平,表示了左右两边的相等关系。
预设3:方程是把未知数当成已知数,顺着题意想,找到相等关系,就能列出方程。
1分钟
五、
课后
练习
1.数学书第66页第1题。
2.数学书第66页第3题。
