湘教版2021-2022学年七年级上册数学2.2 列代数式 同步练习(word版含答案)
文档属性
| 名称 | 湘教版2021-2022学年七年级上册数学2.2 列代数式 同步练习(word版含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 180.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-19 06:58:11 | ||
图片预览




文档简介
《2.2列代数式》同步训练
姓名__________小组____________
一、选择题(
本大题共10小题,共40分)
1.(4分)用代数式表示:a的2倍与3的和.下列表示正确的是( )
A.2a﹣3
B.2a+3
C.2(a﹣3)
D.2(a+3)
2.(4分)已知苹果每千克m元,则2千克苹果共多少元?( )
A.m﹣2
B.m+2
C.
D.2m
3.(4分)用正三角形、正四边形和正六四边形按如图所示的规律拼图案,则第n个图案中正三角形的个数为( )(用含n的代数式表示)
A.2n+1
B.3n+2
C.4n+2
D.4n﹣2
4.(4分)如图,一个窗户的上部是由4个扇形组成的半圆,下部是由4个边长相同的小正方形组成的长方形,则这个窗户的外框总长为( )
A.6a+πa
B.12a
C.15a+πa
D.6a
5.(4分)甲从商贩A处购买了若干斤西瓜,又从商贩B处购买了若干斤西瓜.A、B两处所购买的西瓜重量之比为3:2,然后将买回的西瓜以从A、B两处购买单价的平均数为单价全部卖给了乙,结果发现他赔钱了,这是因为( )
A.商贩A的单价大于商贩B的单价
B.商贩A的单价等于商贩B的单价
C.商版A的单价小于商贩B的单价
D.赔钱与商贩A、商贩B的单价无关
6.(4分)小强购买绿、橙两种颜色的珠子串成一条手链,已知绿色珠子a个,每个2元,橙色珠子b个,每个5元,那么小强购买珠子共需花费( )
A.(2a+5b)元
B.(5a+2b)元
C.2(a+5b)元
D.5(2a+b)元
7.(4分)苹果的单价为a元/千克,香蕉的单价为b元/千克,买2千克苹果和3千克香蕉共需( )
A.(a+b)元
B.(3a+2b)元
C.(2a+3b)元
D.5(a+b)元
8.(4分)观察图中的“品”字形中个数之间的规律,根据观察到的规律得出a的值为( )
A.75
B.89
C.103
D.139
9.(4分)已知轮船在静水中的速度是a千米/小时,水流的速度是5千米/小时,某轮船顺水航行3小时,则轮船航行( )千米.
A.3a
B.3(a+5)
C.3a+5
D.a+15
10.(4分)在比例尺为1:m的地图上,规划出长a厘米,宽b厘米的矩形工业园区,该园区的实际面积是( )平方米.
A.
B.
C.
D.
二、填空题(
本大题共5小题,共20分)
11.(4分)邻居张大伯因病住院,手术费为x元,其他费用为y元,由于参加合作医疗,手术费用报销90%,其他费用报销60%,则张大伯此次住院可报销
元(用代数式表示)
12.(4分)1条直线可以将平面分成2个部分,2条直线最多可以将平面分成4个部分,3条直线最多可以将平面分成7个部分,4条直线最多可将平面分成11个部分,…,9条直线最多可以将平面分成
个部分,…,n条直角最多可以将平面分成
个部分.
13.(4分)a、b两数的平方和减去a与b的乘积的2倍,用代数式表示为
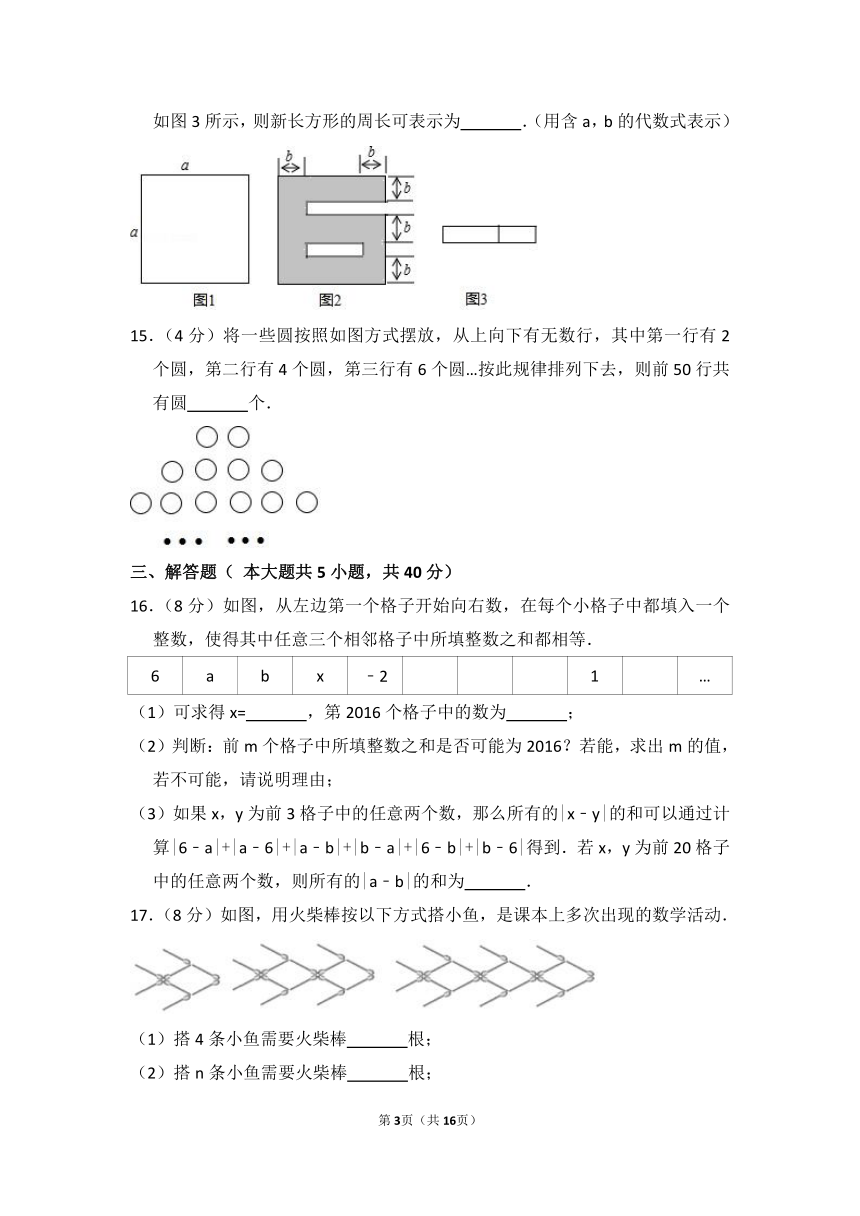
14.(4分)如图1,将一个边长为a的正方形纸片剪去两个小长方形,得到一个“”的图案,如图2所示,再将剪下的两个小长方形拼成一个新的长方形,如图3所示,则新长方形的周长可表示为
.(用含a,b的代数式表示)
15.(4分)将一些圆按照如图方式摆放,从上向下有无数行,其中第一行有2个圆,第二行有4个圆,第三行有6个圆…按此规律排列下去,则前50行共有圆
个.
三、解答题(
本大题共5小题,共40分)
16.(8分)如图,从左边第一个格子开始向右数,在每个小格子中都填入一个整数,使得其中任意三个相邻格子中所填整数之和都相等.
6
a
b
x
﹣2
1
…
(1)可求得x=
,第2016个格子中的数为
;
(2)判断:前m个格子中所填整数之和是否可能为2016?若能,求出m的值,若不可能,请说明理由;
(3)如果x,y为前3格子中的任意两个数,那么所有的|x﹣y|的和可以通过计算|6﹣a|+|a﹣6|+|a﹣b|+|b﹣a|+|6﹣b|+|b﹣6|得到.若x,y为前20格子中的任意两个数,则所有的|a﹣b|的和为
.
17.(8分)如图,用火柴棒按以下方式搭小鱼,是课本上多次出现的数学活动.
(1)搭4条小鱼需要火柴棒
根;
(2)搭n条小鱼需要火柴棒
根;
(3)若搭n朵某种小花需要火柴棒(3n+44)根,现有一堆火柴棒,可以全部用上搭出m条小鱼,也可以全部用上搭出m朵小花,求m的值及这堆火柴棒的数量.
18.(8分)测得一种树苗的高度与树苗生长的年数的有关数据如下表(树苗原高100cm)
年数(n)
高度(cm)
1
100+12
2
100+24
3
100+36
4
100+48
……
……
假设以后各年树苗高度的变化与年数的关系保持上述关系,回答下列问题:
(1)生长了10年的树高是
cm,用式子表示生长了n年的树高是
cm.
(2)种植该种树多少年后,树高才能达到2.8m?
19.(8分)有一根铁丝长为am,第一次用去一半少1m,第二次用去剩下的一半多1m,这条铁丝还剩余多少米?
20.(8分)如图是某种窗户的形状,其上部是半圆形,下部是边长相同的四个小正方形,已知下部分每小正方形的边长为acm,求:
(1)窗户的面积S;
(2)窗框用料(实线部分)的总长度L.(答案用π表示)
参考答案与试题解析
一、选择题(
本大题共10小题,共40分)
1.(4分)用代数式表示:a的2倍与3的和.下列表示正确的是( )
A.2a﹣3
B.2a+3
C.2(a﹣3)
D.2(a+3)
【分析】a的2倍就是2a,与3的和就是2a+3,根据题目中的运算顺序就可以列出式子,从而得出结论.
【解答】解:a的2倍就是:2a,
a的2倍与3的和就是:2a与3的和,可表示为:2a+3.
故选:B.
【点评】本题是一道列代数式的文字题,本题考查了数量之间的和差倍的关系.解答时理清关系的运算顺序是解答的关键.
2.(4分)已知苹果每千克m元,则2千克苹果共多少元?( )
A.m﹣2
B.m+2
C.
D.2m
【分析】根据苹果每千克m元,可以用代数式表示出2千克苹果的价钱.
【解答】解:∵苹果每千克m元,
∴2千克苹果2m元,
故选:D.
【点评】本题考查列代数式,解答本题的关键是明确题意,列出相应的代数式.
3.(4分)用正三角形、正四边形和正六四边形按如图所示的规律拼图案,则第n个图案中正三角形的个数为( )(用含n的代数式表示)
A.2n+1
B.3n+2
C.4n+2
D.4n﹣2
【分析】设第n个图案中正三角形的个数为an,观察图案找出a1,a2,a3,…,的值,根据数的变化,即可找出an=6+4(n﹣1)=4n+2,此题得解.
【解答】解:设第n个图案中正三角形的个数为an.
∵a1=6,a2=6+4=10,a3=6+4+4=14,…,
∴an=6+4(n﹣1)=4n+2.
故选:C.
【点评】本题考查了规律型:图形的变化类以及列代数式,根据图形的变化找出an=4n+2是解题的关键.
4.(4分)如图,一个窗户的上部是由4个扇形组成的半圆,下部是由4个边长相同的小正方形组成的长方形,则这个窗户的外框总长为( )
A.6a+πa
B.12a
C.15a+πa
D.6a
【分析】先求出上半圆的直径为2a,即可得出结论.
【解答】解:由题意知,上半圆的直径为2a,
∴窗户的外框总长为2a×3+×π×2a=6a+πa,
故选:A.
【点评】此题主要考列代数式,圆的周长公式,确定出半圆的直径是解本题的关键.
5.(4分)甲从商贩A处购买了若干斤西瓜,又从商贩B处购买了若干斤西瓜.A、B两处所购买的西瓜重量之比为3:2,然后将买回的西瓜以从A、B两处购买单价的平均数为单价全部卖给了乙,结果发现他赔钱了,这是因为( )
A.商贩A的单价大于商贩B的单价
B.商贩A的单价等于商贩B的单价
C.商版A的单价小于商贩B的单价
D.赔钱与商贩A、商贩B的单价无关
【分析】本题考查一元一次不等式组的应用,将现实生活中的事件与数学思想联系起来,读懂题列出不等式关系式即可求解.
【解答】解:利润=总售价﹣总成本=×5﹣(3a+2b)=0.5b﹣0.5a,赔钱了说明利润<0
∴0.5b﹣0.5a<0,
∴a>b.
故选:A.
【点评】此题考查一元一次不等式组的应用,解决本题的关键是读懂题意,找到符合题意的不等关系式.
6.(4分)小强购买绿、橙两种颜色的珠子串成一条手链,已知绿色珠子a个,每个2元,橙色珠子b个,每个5元,那么小强购买珠子共需花费( )
A.(2a+5b)元
B.(5a+2b)元
C.2(a+5b)元
D.5(2a+b)元
【分析】直接利用两种颜色的珠子的价格进而求出手链的价格.
【解答】解:∵绿色珠子每个2元,橙色珠子每个5元,
∴小强购买珠子共需花费(2a+5b)元,
故选:A.
【点评】此题主要考查了列代数式,正确得出各种颜色珠子的数量是解题关键.
7.(4分)苹果的单价为a元/千克,香蕉的单价为b元/千克,买2千克苹果和3千克香蕉共需( )
A.(a+b)元
B.(3a+2b)元
C.(2a+3b)元
D.5(a+b)元
【分析】根据题意列出代数式即可.
【解答】解:根据题意得:买2千克苹果和3千克香蕉共需(2a+3b)元,
故选:C.
【点评】此题考查了列代数式,弄清题意是解本题的关键.
8.(4分)观察图中的“品”字形中个数之间的规律,根据观察到的规律得出a的值为( )
A.75
B.89
C.103
D.139
【分析】由1、3、5、…为连续的奇数可知,11所在“品”字形为第6个图形,由左下的数字为2、4、8、…可得出b=26=64,再由右下数字为上面数字加左下数字,即可求出a值.
【解答】解:∵“品”字形中上面的数字为连续的奇数,左下的数字为2、4、8、…,
∴11所在“品”字形为第6个图形,
∴b=26=64.
又∵1+2=3,3+4=7,5+8=13,…,
∴a=11+b=75.
故选:A.
【点评】本题考查了规律型中数字的变化类,根据“品”字形中数字的变化,找出变化规律是解题的关键.
9.(4分)已知轮船在静水中的速度是a千米/小时,水流的速度是5千米/小时,某轮船顺水航行3小时,则轮船航行( )千米.
A.3a
B.3(a+5)
C.3a+5
D.a+15
【分析】根据路程等于速度乘以时间的等量关系即可求出答案.
【解答】解:根据题意知轮船顺水航行的速度为(a+5)千米/小时,
所以轮船顺水航行3小时的路程为3(a+5)千米,
故选:B.
【点评】此题考查列代数式,掌握静水速度、水流速度、顺水速度、逆水速度之间的关系是解决问题的关键.
10.(4分)在比例尺为1:m的地图上,规划出长a厘米,宽b厘米的矩形工业园区,该园区的实际面积是( )平方米.
A.
B.
C.
D.
【分析】先设该园区的实际面积是xcm2,然后由比例尺的定义列方程:=()2,解此方程即可求得答案.
【解答】解:设该园区的实际面积是xcm2,
∵地图上长a厘米,宽b厘米的矩形工业园区的面积为:ab平方厘米,根据题意得:=()2,
∴x=abm2,
abm2平方厘米=平方米.
故选:A.
【点评】此题考查了列代数式和比例尺的定义.此题难度不大,解题的关键是注意方程思想的应用,注意统一单位.
二、填空题(
本大题共5小题,共20分)
11.(4分)邻居张大伯因病住院,手术费为x元,其他费用为y元,由于参加合作医疗,手术费用报销90%,其他费用报销60%,则张大伯此次住院可报销 (0.9x+0.6y) 元(用代数式表示)
【分析】根据手术费为x元,其他费用为y元,手术费用报销90%,其他费用报销60%,列出代数式,即可求出答案.
【解答】解:因为手术费为x元,其他费用为y元,
手术费用报销90%,其他费用报销60%,
所以张大伯此次住院可报销x?90%+y?60%=0.9x+0.6y(元).
故答案为:(0.9x+0.6y).
【点评】此题考查了列代数式,解决问题的关键是读懂题意,找到所求的量的等量关系.
12.(4分)1条直线可以将平面分成2个部分,2条直线最多可以将平面分成4个部分,3条直线最多可以将平面分成7个部分,4条直线最多可将平面分成11个部分,…,9条直线最多可以将平面分成 46 个部分,…,n条直角最多可以将平面分成 +1 个部分.
【分析】根据题意找出一般性规律,写出即可.
【解答】解:9条直线最多可以将平面分成46个部分,n条直角最多可以将平面分成1+1+2+3+…+n=+1,
故答案为:+1
【点评】此题考查了规律型:图形的变化类,弄清题中的规律是解本题的关键.
13.(4分)a、b两数的平方和减去a与b的乘积的2倍,用代数式表示为 a2+b2﹣2ab
【分析】被减数为:a、b两数的平方和.减数为:a与b的乘积的2倍.
【解答】解:a、b两数的平方和的代数式是a2+b2.a与b乘积的2倍的代数式是2ab,
所以a、b两数的平方和减去a与b的乘积的2倍,用代数式表示为a2+b2﹣2ab.
故答案为a2+b2﹣2ab.
【点评】此题考查了列代数式,解题关键是根据题意,用代数式去表示每一个条件.
14.(4分)如图1,将一个边长为a的正方形纸片剪去两个小长方形,得到一个“”的图案,如图2所示,再将剪下的两个小长方形拼成一个新的长方形,如图3所示,则新长方形的周长可表示为 5a﹣9b .(用含a,b的代数式表示)
【分析】剪下的上面一个小矩形的长为a﹣b,下面一个小矩形的长为a﹣2b,宽都是(a﹣3b),所以这两个小矩形拼成的新矩形的长为a﹣b+a﹣2b,宽为(a﹣3b),然后计算这个新矩形的周长.
【解答】解:新矩形的周长为2[(a﹣b)+(a﹣2b)+(a﹣3b)]=5a﹣9b.
故答案为5a﹣9b.
【点评】本题考查了列代数式:把问题中与数量有关的词语,用含有数字、字母和运算符号的式子表示出来,就是列代数式.解决本题的关键用a和b表示出剪下的两个小矩形的长与宽.
15.(4分)将一些圆按照如图方式摆放,从上向下有无数行,其中第一行有2个圆,第二行有4个圆,第三行有6个圆…按此规律排列下去,则前50行共有圆 2550 个.
【分析】先找出规律,确定出第n行圆的个数为2n个,即:第50行为100个,进而求2+4+6+8+…+100即可得出结论.
【解答】解:∵第一行有2个圆,
第二行有4个圆,
第三行有6个圆,
…
∴第n行有2n个圆,
∴前50行共有圆:2+4+6+8+…+2×50=2+4+6+8+…+100=2550个,
故答案为:2550
【点评】本题主要考查图形的变化规律,解题的关键是根据题意得出每行圆的个数即为行数的2倍.
三、解答题(
本大题共5小题,共40分)
16.(8分)如图,从左边第一个格子开始向右数,在每个小格子中都填入一个整数,使得其中任意三个相邻格子中所填整数之和都相等.
6
a
b
x
﹣2
1
…
(1)可求得x= 6 ,第2016个格子中的数为 1 ;
(2)判断:前m个格子中所填整数之和是否可能为2016?若能,求出m的值,若不可能,请说明理由;
(3)如果x,y为前3格子中的任意两个数,那么所有的|x﹣y|的和可以通过计算|6﹣a|+|a﹣6|+|a﹣b|+|b﹣a|+|6﹣b|+|b﹣6|得到.若x,y为前20格子中的任意两个数,则所有的|a﹣b|的和为 1386 .
【分析】(1)根据题意,归纳总结得到所求数字即可;
(2)可先计算出这三个数的和,再照规律计算.
(3)由于是三个数重复出现,因此可用前三个数的重复多次计算出结果.
【解答】解:(1)∵6+a+b=a+b+x
∴x=6
进而可得a=﹣2,b=1;
表中数字的规律是6,﹣2,1,6,﹣2,1,…循环,2016除以3等于672.
所以第2016位应该是1.
故答案是:6,1.
(2)不可能.由于表格中的数是6,﹣2,1,6,﹣2,1,…循环,前三个数的和是5.而2016除以5等于403余1,也就是说前403×3=1209位之和是5×403=2015.而第1210位是6.
所以前m个格子中所填整数之和是不可能的.
(3)由于是三个数重复出现,前20个格子中,这三个数中,6和﹣2出现了7次,1出现了6次.故代入式子可得:(|6+2|×7+|6﹣1|×6)×7+(|﹣2﹣6|×7+|﹣2﹣1|×6)×7+(|1﹣6|×7+|1+2|×7)×6=1386.
故答案为:1386.
【点评】本题考查了列一元一次方程解实际问题的运用,规律推导的运用,此类题的关键是找出是按什么规律变化的,然后再按规律找出字母所代表的数,再进行进一步的计算.
17.(8分)如图,用火柴棒按以下方式搭小鱼,是课本上多次出现的数学活动.
(1)搭4条小鱼需要火柴棒 26 根;
(2)搭n条小鱼需要火柴棒 (6n+2) 根;
(3)若搭n朵某种小花需要火柴棒(3n+44)根,现有一堆火柴棒,可以全部用上搭出m条小鱼,也可以全部用上搭出m朵小花,求m的值及这堆火柴棒的数量.
【分析】(1)根据图形可得搭1条小鱼需要火柴棒8根,搭2条小鱼需要火柴棒14根,搭3条小鱼需要火柴棒20根,即每增加1条小鱼,火柴棒增加6根,由此得出搭4条小鱼需要火柴棒26根;
(2)根据图形可得后一个图形中火柴数量是前一个图形火柴数量加6,根据题意,求出搭n条小鱼需要用(6n+2)根火柴棒.
(3)根据题意得6m+2=3m+44,可得答案.
【解答】解:(1)根据题意,可得搭4条小鱼需要火柴棒26根.
故答案为26;
(2)根据题意,可得搭n条小鱼需要火柴棒(6n+2)根.
故答案为(6n+2);
(3)根据题意,可得6m+2=3m+44,
解得m=14,
此时6m+2=6×14+2=86.
故m=14,这堆火柴棒的数量是86根.
【点评】此题主要考查了规律型:图形的变化类,首先应找出发生变化的位置,并且观察变化规律.注意由特殊到一般的分析方法.
18.(8分)测得一种树苗的高度与树苗生长的年数的有关数据如下表(树苗原高100cm)
年数(n)
高度(cm)
1
100+12
2
100+24
3
100+36
4
100+48
……
……
假设以后各年树苗高度的变化与年数的关系保持上述关系,回答下列问题:
(1)生长了10年的树高是 220 cm,用式子表示生长了n年的树高是 (100+12n) cm.
(2)种植该种树多少年后,树高才能达到2.8m?
【分析】(1)由图表可知生长了1年的树高为100+12;生长了2年的树高为100+2×12;生长了3年的树高为100+3×12;故可得生长了10年的树高为100+10×12;生长了n年的树高为100+12n;
(2)根据种植该种树n年后,树高才能达到2.8m列出方程100+12n=280,解方程即可.
【解答】解:(1)生长了10年的树高是100+10×12=220cm,
生长了n年的树高是(100+12n)cm.
故答案为220,(100+12n);
(2)设种植该种树n年后,树高达到2.8m.
由题意,得100+12n=280,
解得n=15.
答:种植该种树15年后,树高才能达到2.8m.
【点评】本题考查了规律型:数字的变化类,解决本题的关键是根据所给的图表发现规律,得到树苗的高度与树苗生长的年数之间的关系.
19.(8分)有一根铁丝长为am,第一次用去一半少1m,第二次用去剩下的一半多1m,这条铁丝还剩余多少米?
【分析】第一次用去a﹣1,第二次用去[a﹣(a﹣1)]+1,用a减去这两次的总量可得.
【解答】解:根据题意,用去两次后还剩a﹣(a﹣1)﹣[a﹣(a﹣1)]﹣1=a﹣,
答:这条铁丝还剩余(a﹣)米
【点评】本题主要考查列代数式能力,根据题意表示出这两次用去的长度是关键.
20.(8分)如图是某种窗户的形状,其上部是半圆形,下部是边长相同的四个小正方形,已知下部分每小正方形的边长为acm,求:
(1)窗户的面积S;
(2)窗框用料(实线部分)的总长度L.(答案用π表示)
【分析】(1)窗户面积为:4个小正方形的面积+半圆的面积;
(2)窗框用料(实线部分)的总长度为所有小正方形的边长之和+半个圆的弧长.
【解答】解:(1)窗户的面积S=(4a2+πa2)平方米;
(2)窗框用料(实线部分)的总长度L=(12a+πa)米.
【点评】本题考查了列代数式,解决问题的关键是读懂题意,找到所求的量的等量关系.本题需注意:窗框用料的总长度指的是所有实线的长度.
第1页(共3页)
姓名__________小组____________
一、选择题(
本大题共10小题,共40分)
1.(4分)用代数式表示:a的2倍与3的和.下列表示正确的是( )
A.2a﹣3
B.2a+3
C.2(a﹣3)
D.2(a+3)
2.(4分)已知苹果每千克m元,则2千克苹果共多少元?( )
A.m﹣2
B.m+2
C.
D.2m
3.(4分)用正三角形、正四边形和正六四边形按如图所示的规律拼图案,则第n个图案中正三角形的个数为( )(用含n的代数式表示)
A.2n+1
B.3n+2
C.4n+2
D.4n﹣2
4.(4分)如图,一个窗户的上部是由4个扇形组成的半圆,下部是由4个边长相同的小正方形组成的长方形,则这个窗户的外框总长为( )
A.6a+πa
B.12a
C.15a+πa
D.6a
5.(4分)甲从商贩A处购买了若干斤西瓜,又从商贩B处购买了若干斤西瓜.A、B两处所购买的西瓜重量之比为3:2,然后将买回的西瓜以从A、B两处购买单价的平均数为单价全部卖给了乙,结果发现他赔钱了,这是因为( )
A.商贩A的单价大于商贩B的单价
B.商贩A的单价等于商贩B的单价
C.商版A的单价小于商贩B的单价
D.赔钱与商贩A、商贩B的单价无关
6.(4分)小强购买绿、橙两种颜色的珠子串成一条手链,已知绿色珠子a个,每个2元,橙色珠子b个,每个5元,那么小强购买珠子共需花费( )
A.(2a+5b)元
B.(5a+2b)元
C.2(a+5b)元
D.5(2a+b)元
7.(4分)苹果的单价为a元/千克,香蕉的单价为b元/千克,买2千克苹果和3千克香蕉共需( )
A.(a+b)元
B.(3a+2b)元
C.(2a+3b)元
D.5(a+b)元
8.(4分)观察图中的“品”字形中个数之间的规律,根据观察到的规律得出a的值为( )
A.75
B.89
C.103
D.139
9.(4分)已知轮船在静水中的速度是a千米/小时,水流的速度是5千米/小时,某轮船顺水航行3小时,则轮船航行( )千米.
A.3a
B.3(a+5)
C.3a+5
D.a+15
10.(4分)在比例尺为1:m的地图上,规划出长a厘米,宽b厘米的矩形工业园区,该园区的实际面积是( )平方米.
A.
B.
C.
D.
二、填空题(
本大题共5小题,共20分)
11.(4分)邻居张大伯因病住院,手术费为x元,其他费用为y元,由于参加合作医疗,手术费用报销90%,其他费用报销60%,则张大伯此次住院可报销
元(用代数式表示)
12.(4分)1条直线可以将平面分成2个部分,2条直线最多可以将平面分成4个部分,3条直线最多可以将平面分成7个部分,4条直线最多可将平面分成11个部分,…,9条直线最多可以将平面分成
个部分,…,n条直角最多可以将平面分成
个部分.
13.(4分)a、b两数的平方和减去a与b的乘积的2倍,用代数式表示为
14.(4分)如图1,将一个边长为a的正方形纸片剪去两个小长方形,得到一个“”的图案,如图2所示,再将剪下的两个小长方形拼成一个新的长方形,如图3所示,则新长方形的周长可表示为
.(用含a,b的代数式表示)
15.(4分)将一些圆按照如图方式摆放,从上向下有无数行,其中第一行有2个圆,第二行有4个圆,第三行有6个圆…按此规律排列下去,则前50行共有圆
个.
三、解答题(
本大题共5小题,共40分)
16.(8分)如图,从左边第一个格子开始向右数,在每个小格子中都填入一个整数,使得其中任意三个相邻格子中所填整数之和都相等.
6
a
b
x
﹣2
1
…
(1)可求得x=
,第2016个格子中的数为
;
(2)判断:前m个格子中所填整数之和是否可能为2016?若能,求出m的值,若不可能,请说明理由;
(3)如果x,y为前3格子中的任意两个数,那么所有的|x﹣y|的和可以通过计算|6﹣a|+|a﹣6|+|a﹣b|+|b﹣a|+|6﹣b|+|b﹣6|得到.若x,y为前20格子中的任意两个数,则所有的|a﹣b|的和为
.
17.(8分)如图,用火柴棒按以下方式搭小鱼,是课本上多次出现的数学活动.
(1)搭4条小鱼需要火柴棒
根;
(2)搭n条小鱼需要火柴棒
根;
(3)若搭n朵某种小花需要火柴棒(3n+44)根,现有一堆火柴棒,可以全部用上搭出m条小鱼,也可以全部用上搭出m朵小花,求m的值及这堆火柴棒的数量.
18.(8分)测得一种树苗的高度与树苗生长的年数的有关数据如下表(树苗原高100cm)
年数(n)
高度(cm)
1
100+12
2
100+24
3
100+36
4
100+48
……
……
假设以后各年树苗高度的变化与年数的关系保持上述关系,回答下列问题:
(1)生长了10年的树高是
cm,用式子表示生长了n年的树高是
cm.
(2)种植该种树多少年后,树高才能达到2.8m?
19.(8分)有一根铁丝长为am,第一次用去一半少1m,第二次用去剩下的一半多1m,这条铁丝还剩余多少米?
20.(8分)如图是某种窗户的形状,其上部是半圆形,下部是边长相同的四个小正方形,已知下部分每小正方形的边长为acm,求:
(1)窗户的面积S;
(2)窗框用料(实线部分)的总长度L.(答案用π表示)
参考答案与试题解析
一、选择题(
本大题共10小题,共40分)
1.(4分)用代数式表示:a的2倍与3的和.下列表示正确的是( )
A.2a﹣3
B.2a+3
C.2(a﹣3)
D.2(a+3)
【分析】a的2倍就是2a,与3的和就是2a+3,根据题目中的运算顺序就可以列出式子,从而得出结论.
【解答】解:a的2倍就是:2a,
a的2倍与3的和就是:2a与3的和,可表示为:2a+3.
故选:B.
【点评】本题是一道列代数式的文字题,本题考查了数量之间的和差倍的关系.解答时理清关系的运算顺序是解答的关键.
2.(4分)已知苹果每千克m元,则2千克苹果共多少元?( )
A.m﹣2
B.m+2
C.
D.2m
【分析】根据苹果每千克m元,可以用代数式表示出2千克苹果的价钱.
【解答】解:∵苹果每千克m元,
∴2千克苹果2m元,
故选:D.
【点评】本题考查列代数式,解答本题的关键是明确题意,列出相应的代数式.
3.(4分)用正三角形、正四边形和正六四边形按如图所示的规律拼图案,则第n个图案中正三角形的个数为( )(用含n的代数式表示)
A.2n+1
B.3n+2
C.4n+2
D.4n﹣2
【分析】设第n个图案中正三角形的个数为an,观察图案找出a1,a2,a3,…,的值,根据数的变化,即可找出an=6+4(n﹣1)=4n+2,此题得解.
【解答】解:设第n个图案中正三角形的个数为an.
∵a1=6,a2=6+4=10,a3=6+4+4=14,…,
∴an=6+4(n﹣1)=4n+2.
故选:C.
【点评】本题考查了规律型:图形的变化类以及列代数式,根据图形的变化找出an=4n+2是解题的关键.
4.(4分)如图,一个窗户的上部是由4个扇形组成的半圆,下部是由4个边长相同的小正方形组成的长方形,则这个窗户的外框总长为( )
A.6a+πa
B.12a
C.15a+πa
D.6a
【分析】先求出上半圆的直径为2a,即可得出结论.
【解答】解:由题意知,上半圆的直径为2a,
∴窗户的外框总长为2a×3+×π×2a=6a+πa,
故选:A.
【点评】此题主要考列代数式,圆的周长公式,确定出半圆的直径是解本题的关键.
5.(4分)甲从商贩A处购买了若干斤西瓜,又从商贩B处购买了若干斤西瓜.A、B两处所购买的西瓜重量之比为3:2,然后将买回的西瓜以从A、B两处购买单价的平均数为单价全部卖给了乙,结果发现他赔钱了,这是因为( )
A.商贩A的单价大于商贩B的单价
B.商贩A的单价等于商贩B的单价
C.商版A的单价小于商贩B的单价
D.赔钱与商贩A、商贩B的单价无关
【分析】本题考查一元一次不等式组的应用,将现实生活中的事件与数学思想联系起来,读懂题列出不等式关系式即可求解.
【解答】解:利润=总售价﹣总成本=×5﹣(3a+2b)=0.5b﹣0.5a,赔钱了说明利润<0
∴0.5b﹣0.5a<0,
∴a>b.
故选:A.
【点评】此题考查一元一次不等式组的应用,解决本题的关键是读懂题意,找到符合题意的不等关系式.
6.(4分)小强购买绿、橙两种颜色的珠子串成一条手链,已知绿色珠子a个,每个2元,橙色珠子b个,每个5元,那么小强购买珠子共需花费( )
A.(2a+5b)元
B.(5a+2b)元
C.2(a+5b)元
D.5(2a+b)元
【分析】直接利用两种颜色的珠子的价格进而求出手链的价格.
【解答】解:∵绿色珠子每个2元,橙色珠子每个5元,
∴小强购买珠子共需花费(2a+5b)元,
故选:A.
【点评】此题主要考查了列代数式,正确得出各种颜色珠子的数量是解题关键.
7.(4分)苹果的单价为a元/千克,香蕉的单价为b元/千克,买2千克苹果和3千克香蕉共需( )
A.(a+b)元
B.(3a+2b)元
C.(2a+3b)元
D.5(a+b)元
【分析】根据题意列出代数式即可.
【解答】解:根据题意得:买2千克苹果和3千克香蕉共需(2a+3b)元,
故选:C.
【点评】此题考查了列代数式,弄清题意是解本题的关键.
8.(4分)观察图中的“品”字形中个数之间的规律,根据观察到的规律得出a的值为( )
A.75
B.89
C.103
D.139
【分析】由1、3、5、…为连续的奇数可知,11所在“品”字形为第6个图形,由左下的数字为2、4、8、…可得出b=26=64,再由右下数字为上面数字加左下数字,即可求出a值.
【解答】解:∵“品”字形中上面的数字为连续的奇数,左下的数字为2、4、8、…,
∴11所在“品”字形为第6个图形,
∴b=26=64.
又∵1+2=3,3+4=7,5+8=13,…,
∴a=11+b=75.
故选:A.
【点评】本题考查了规律型中数字的变化类,根据“品”字形中数字的变化,找出变化规律是解题的关键.
9.(4分)已知轮船在静水中的速度是a千米/小时,水流的速度是5千米/小时,某轮船顺水航行3小时,则轮船航行( )千米.
A.3a
B.3(a+5)
C.3a+5
D.a+15
【分析】根据路程等于速度乘以时间的等量关系即可求出答案.
【解答】解:根据题意知轮船顺水航行的速度为(a+5)千米/小时,
所以轮船顺水航行3小时的路程为3(a+5)千米,
故选:B.
【点评】此题考查列代数式,掌握静水速度、水流速度、顺水速度、逆水速度之间的关系是解决问题的关键.
10.(4分)在比例尺为1:m的地图上,规划出长a厘米,宽b厘米的矩形工业园区,该园区的实际面积是( )平方米.
A.
B.
C.
D.
【分析】先设该园区的实际面积是xcm2,然后由比例尺的定义列方程:=()2,解此方程即可求得答案.
【解答】解:设该园区的实际面积是xcm2,
∵地图上长a厘米,宽b厘米的矩形工业园区的面积为:ab平方厘米,根据题意得:=()2,
∴x=abm2,
abm2平方厘米=平方米.
故选:A.
【点评】此题考查了列代数式和比例尺的定义.此题难度不大,解题的关键是注意方程思想的应用,注意统一单位.
二、填空题(
本大题共5小题,共20分)
11.(4分)邻居张大伯因病住院,手术费为x元,其他费用为y元,由于参加合作医疗,手术费用报销90%,其他费用报销60%,则张大伯此次住院可报销 (0.9x+0.6y) 元(用代数式表示)
【分析】根据手术费为x元,其他费用为y元,手术费用报销90%,其他费用报销60%,列出代数式,即可求出答案.
【解答】解:因为手术费为x元,其他费用为y元,
手术费用报销90%,其他费用报销60%,
所以张大伯此次住院可报销x?90%+y?60%=0.9x+0.6y(元).
故答案为:(0.9x+0.6y).
【点评】此题考查了列代数式,解决问题的关键是读懂题意,找到所求的量的等量关系.
12.(4分)1条直线可以将平面分成2个部分,2条直线最多可以将平面分成4个部分,3条直线最多可以将平面分成7个部分,4条直线最多可将平面分成11个部分,…,9条直线最多可以将平面分成 46 个部分,…,n条直角最多可以将平面分成 +1 个部分.
【分析】根据题意找出一般性规律,写出即可.
【解答】解:9条直线最多可以将平面分成46个部分,n条直角最多可以将平面分成1+1+2+3+…+n=+1,
故答案为:+1
【点评】此题考查了规律型:图形的变化类,弄清题中的规律是解本题的关键.
13.(4分)a、b两数的平方和减去a与b的乘积的2倍,用代数式表示为 a2+b2﹣2ab
【分析】被减数为:a、b两数的平方和.减数为:a与b的乘积的2倍.
【解答】解:a、b两数的平方和的代数式是a2+b2.a与b乘积的2倍的代数式是2ab,
所以a、b两数的平方和减去a与b的乘积的2倍,用代数式表示为a2+b2﹣2ab.
故答案为a2+b2﹣2ab.
【点评】此题考查了列代数式,解题关键是根据题意,用代数式去表示每一个条件.
14.(4分)如图1,将一个边长为a的正方形纸片剪去两个小长方形,得到一个“”的图案,如图2所示,再将剪下的两个小长方形拼成一个新的长方形,如图3所示,则新长方形的周长可表示为 5a﹣9b .(用含a,b的代数式表示)
【分析】剪下的上面一个小矩形的长为a﹣b,下面一个小矩形的长为a﹣2b,宽都是(a﹣3b),所以这两个小矩形拼成的新矩形的长为a﹣b+a﹣2b,宽为(a﹣3b),然后计算这个新矩形的周长.
【解答】解:新矩形的周长为2[(a﹣b)+(a﹣2b)+(a﹣3b)]=5a﹣9b.
故答案为5a﹣9b.
【点评】本题考查了列代数式:把问题中与数量有关的词语,用含有数字、字母和运算符号的式子表示出来,就是列代数式.解决本题的关键用a和b表示出剪下的两个小矩形的长与宽.
15.(4分)将一些圆按照如图方式摆放,从上向下有无数行,其中第一行有2个圆,第二行有4个圆,第三行有6个圆…按此规律排列下去,则前50行共有圆 2550 个.
【分析】先找出规律,确定出第n行圆的个数为2n个,即:第50行为100个,进而求2+4+6+8+…+100即可得出结论.
【解答】解:∵第一行有2个圆,
第二行有4个圆,
第三行有6个圆,
…
∴第n行有2n个圆,
∴前50行共有圆:2+4+6+8+…+2×50=2+4+6+8+…+100=2550个,
故答案为:2550
【点评】本题主要考查图形的变化规律,解题的关键是根据题意得出每行圆的个数即为行数的2倍.
三、解答题(
本大题共5小题,共40分)
16.(8分)如图,从左边第一个格子开始向右数,在每个小格子中都填入一个整数,使得其中任意三个相邻格子中所填整数之和都相等.
6
a
b
x
﹣2
1
…
(1)可求得x= 6 ,第2016个格子中的数为 1 ;
(2)判断:前m个格子中所填整数之和是否可能为2016?若能,求出m的值,若不可能,请说明理由;
(3)如果x,y为前3格子中的任意两个数,那么所有的|x﹣y|的和可以通过计算|6﹣a|+|a﹣6|+|a﹣b|+|b﹣a|+|6﹣b|+|b﹣6|得到.若x,y为前20格子中的任意两个数,则所有的|a﹣b|的和为 1386 .
【分析】(1)根据题意,归纳总结得到所求数字即可;
(2)可先计算出这三个数的和,再照规律计算.
(3)由于是三个数重复出现,因此可用前三个数的重复多次计算出结果.
【解答】解:(1)∵6+a+b=a+b+x
∴x=6
进而可得a=﹣2,b=1;
表中数字的规律是6,﹣2,1,6,﹣2,1,…循环,2016除以3等于672.
所以第2016位应该是1.
故答案是:6,1.
(2)不可能.由于表格中的数是6,﹣2,1,6,﹣2,1,…循环,前三个数的和是5.而2016除以5等于403余1,也就是说前403×3=1209位之和是5×403=2015.而第1210位是6.
所以前m个格子中所填整数之和是不可能的.
(3)由于是三个数重复出现,前20个格子中,这三个数中,6和﹣2出现了7次,1出现了6次.故代入式子可得:(|6+2|×7+|6﹣1|×6)×7+(|﹣2﹣6|×7+|﹣2﹣1|×6)×7+(|1﹣6|×7+|1+2|×7)×6=1386.
故答案为:1386.
【点评】本题考查了列一元一次方程解实际问题的运用,规律推导的运用,此类题的关键是找出是按什么规律变化的,然后再按规律找出字母所代表的数,再进行进一步的计算.
17.(8分)如图,用火柴棒按以下方式搭小鱼,是课本上多次出现的数学活动.
(1)搭4条小鱼需要火柴棒 26 根;
(2)搭n条小鱼需要火柴棒 (6n+2) 根;
(3)若搭n朵某种小花需要火柴棒(3n+44)根,现有一堆火柴棒,可以全部用上搭出m条小鱼,也可以全部用上搭出m朵小花,求m的值及这堆火柴棒的数量.
【分析】(1)根据图形可得搭1条小鱼需要火柴棒8根,搭2条小鱼需要火柴棒14根,搭3条小鱼需要火柴棒20根,即每增加1条小鱼,火柴棒增加6根,由此得出搭4条小鱼需要火柴棒26根;
(2)根据图形可得后一个图形中火柴数量是前一个图形火柴数量加6,根据题意,求出搭n条小鱼需要用(6n+2)根火柴棒.
(3)根据题意得6m+2=3m+44,可得答案.
【解答】解:(1)根据题意,可得搭4条小鱼需要火柴棒26根.
故答案为26;
(2)根据题意,可得搭n条小鱼需要火柴棒(6n+2)根.
故答案为(6n+2);
(3)根据题意,可得6m+2=3m+44,
解得m=14,
此时6m+2=6×14+2=86.
故m=14,这堆火柴棒的数量是86根.
【点评】此题主要考查了规律型:图形的变化类,首先应找出发生变化的位置,并且观察变化规律.注意由特殊到一般的分析方法.
18.(8分)测得一种树苗的高度与树苗生长的年数的有关数据如下表(树苗原高100cm)
年数(n)
高度(cm)
1
100+12
2
100+24
3
100+36
4
100+48
……
……
假设以后各年树苗高度的变化与年数的关系保持上述关系,回答下列问题:
(1)生长了10年的树高是 220 cm,用式子表示生长了n年的树高是 (100+12n) cm.
(2)种植该种树多少年后,树高才能达到2.8m?
【分析】(1)由图表可知生长了1年的树高为100+12;生长了2年的树高为100+2×12;生长了3年的树高为100+3×12;故可得生长了10年的树高为100+10×12;生长了n年的树高为100+12n;
(2)根据种植该种树n年后,树高才能达到2.8m列出方程100+12n=280,解方程即可.
【解答】解:(1)生长了10年的树高是100+10×12=220cm,
生长了n年的树高是(100+12n)cm.
故答案为220,(100+12n);
(2)设种植该种树n年后,树高达到2.8m.
由题意,得100+12n=280,
解得n=15.
答:种植该种树15年后,树高才能达到2.8m.
【点评】本题考查了规律型:数字的变化类,解决本题的关键是根据所给的图表发现规律,得到树苗的高度与树苗生长的年数之间的关系.
19.(8分)有一根铁丝长为am,第一次用去一半少1m,第二次用去剩下的一半多1m,这条铁丝还剩余多少米?
【分析】第一次用去a﹣1,第二次用去[a﹣(a﹣1)]+1,用a减去这两次的总量可得.
【解答】解:根据题意,用去两次后还剩a﹣(a﹣1)﹣[a﹣(a﹣1)]﹣1=a﹣,
答:这条铁丝还剩余(a﹣)米
【点评】本题主要考查列代数式能力,根据题意表示出这两次用去的长度是关键.
20.(8分)如图是某种窗户的形状,其上部是半圆形,下部是边长相同的四个小正方形,已知下部分每小正方形的边长为acm,求:
(1)窗户的面积S;
(2)窗框用料(实线部分)的总长度L.(答案用π表示)
【分析】(1)窗户面积为:4个小正方形的面积+半圆的面积;
(2)窗框用料(实线部分)的总长度为所有小正方形的边长之和+半个圆的弧长.
【解答】解:(1)窗户的面积S=(4a2+πa2)平方米;
(2)窗框用料(实线部分)的总长度L=(12a+πa)米.
【点评】本题考查了列代数式,解决问题的关键是读懂题意,找到所求的量的等量关系.本题需注意:窗框用料的总长度指的是所有实线的长度.
第1页(共3页)
同课章节目录
