第12章 一次函数 章节测试 2021--2022学年沪科版八年级数学上册 (word版 含答案)
文档属性
| 名称 | 第12章 一次函数 章节测试 2021--2022学年沪科版八年级数学上册 (word版 含答案) |
|
|
| 格式 | doc | ||
| 文件大小 | 455.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-19 00:00:00 | ||
图片预览


文档简介
八年级上册《一次函数》章节测试
一
、选择题
(每小题3分,共30分)
1.下列函数(1),(2)
,(3)
,(4)
,(5)
中,是一次函数的有(
)
A.4个
B.3个
C.2个
D.1个
2.
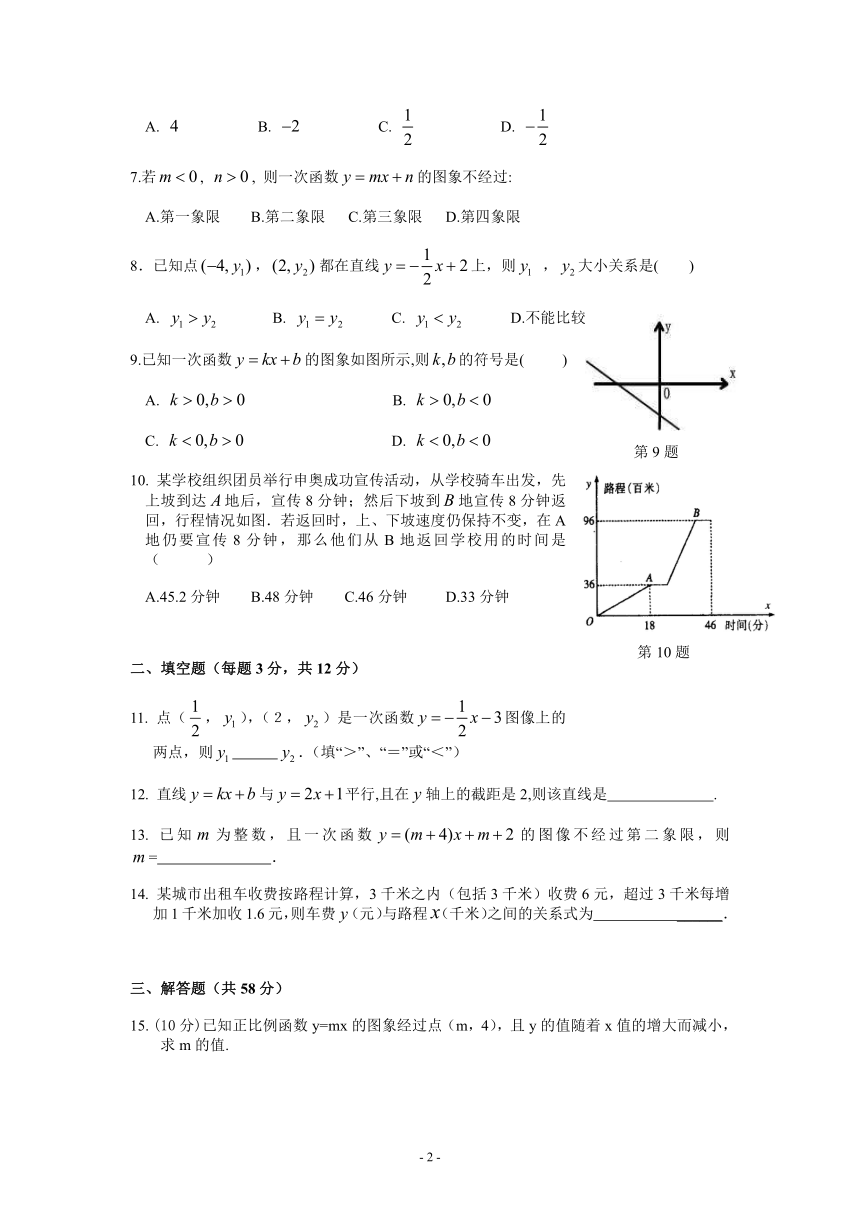
如图,已知点在平面直角坐标系的位置,其坐标可能是(
)
A.(-1,2)
B.(1,2)
C.(-2,-1)
D.(1,-3)
3.
弹簧的长度与所挂物体的质量之间的关系式一次函数关系,图像如图所示,则弹簧本身的长度是
(
)
A.
B.
C.
D.
4.
如果在轴上,那么点的坐标是(
)
A.(-2,0)
B.(0,-2)
C.(1,0)
D.(0,1)
5.
某兴趣小组做实验,将一个装满水的啤酒瓶(上端细、下端粗)倒置,并设法使瓶里的水从瓶中匀速流出。那么该倒置啤酒瓶内水面高度随水流出的时间变化的图象大致是(
)
A
B
C
D
6.
已知一次函数与的图象在轴上相交于同一点,则的值是(
)
A.
B.
C.
D.
7.若,
,
则一次函数的图象不经过:
A.第一象限
B.第二象限
C.第三象限
D.第四象限
8.已知点,都在直线上,则
,大小关系是(
)
A.
B.
C.
D.不能比较
9.已知一次函数的图象如图所示,则的符号是(
)
A.
B.
C.
D.
10.
某学校组织团员举行申奥成功宣传活动,从学校骑车出发,先上坡到达地后,宣传8分钟;然后下坡到地宣传8分钟返回,行程情况如图.若返回时,上、下坡速度仍保持不变,在A地仍要宣传8分钟,那么他们从B地返回学校用的时间是(
)
A.45.2分钟
B.48分钟
C.46分钟
D.33分钟
二、填空题(每题3分,共12分)
11.
点(,),(2,)是一次函数图像上的两点,则 .(填“>”、“=”或“<”)
12.
直线与平行,且在轴上的截距是2,则该直线是
.
13.
已知为整数,且一次函数的图像不经过第二象限,则=
.
14.
某城市出租车收费按路程计算,3千米之内(包括3千米)收费6元,超过3千米每增加1千米加收1.6元,则车费(元)与路程(千米)之间的关系式为
______.
三、解答题(共58分)
15.
(10分)已知正比例函数y=mx的图象经过点(m,4),且y的值随着x值的增大而减小,求m的值.
16.(10分)在平面直角坐标系中,的边在轴上,且,点的坐标为(-5,0),点的坐标为(2,5)。
(1)求点坐标;(2)求的面积。
17.(10分)已知一次函数y=(3m-8)x+1-m图象与
y轴交点在x轴下方,且y随x的增大而减小,其中m为整数,求m的值
.
18.(10分)某电话公司开设了两种手机通讯业务,甲种业务:使用者先缴50元月租费,然后每通话1分钟,再付话费0.4元;乙种业务:不交月租费,每通话1分钟,付话费0.6元(指市话)。若一个月内通话x分钟,两种方式的费用分别为(元)和(元)。
(1)分别求出、与之间的函数关系式。
(2)根据每月可能的通话时间,作为消费者选用哪种缴费方式更实惠。
19.(10分)如图,直线的解析表达式为,且与轴交于点.直线经过点、,直线,交于点.
(1)求点的坐标;
(2)求直线的解析表达式;
(3)求的面积;
(4)在直线上存在异于点的另一个点,使得与的面积相等,求点的坐标。
20.
一辆客车从甲地开往甲地,一辆出租车从乙地开往甲地,两车同时出发,设客车离甲地的距离为y1(km),出租车离甲地的距离为y2(km),客车行驶时间为x(h),y1,y2与x的函数关系图象如图12所示:
(1)根据图象,直接写出y1,y2关于x的函数关系式。
(2)分别求出当x=3,x=5,x=8时,两车之间的距离。
(3)若设两车间的距离为S(km),请写出S关于x的函数关系式。
(4)甲、乙两地间有A、B两个加油站,相距200km,若客车进入A站加油时,出租车恰好进入B站加油。求A加油站到甲地的距离。
八年级上册《一次函数》章节测试
参考答案
选择题:(3分每题,共30分)
1、B
2、D
3、B
4、B
5、A
6、D
7、C
8、A
9、D
10、A
填空题:((3分每题,共12分)
11、;12、;13、;14、.
解答题:(共58分)
(10分)15.解:因为正比例函数y=mx的图象经过点(m,4),
所以4=m·m,解得m=±2……………………………………………..4分
又y的值随着x值的增大而减小,
所以m<0,故m=-2…………………………………………………….10分
(10分)16、(1)设点坐标为,因为,点的坐标为,
所以,解之得:,则点坐标为.……6分,每个坐标3分
(2).…………………………10分
17.m=2…………………………10分
18、(1)由题意可知:,.……………6分,每个3分
(2)假设甲种费用大于乙种费用,即:,则,得,所以当时,选择乙种业务更实惠;假设甲种费用等于乙种费用,即:,则,得,所以当时,两种业务都一样;假设甲种费用小于乙种费用,即:,则,得,所以当时,选择甲种业务更实惠。………10分
19、(1)由图像可设点坐标为,则,得,所以点坐标为.
……………………………………………………………………………………..…2分
(2)设直线的解析式为,有图像可知,得,所以直线的解析式为.………………..4分
(3)由题意得:,解得,所以点坐标为,又因为,所以.……………………7分
(4)设点坐标为,因为要使,即点到的距离也为,所以点坐标可写为,又因为点在直线上,则,得,所以点坐标是.…………10分
20.
(1)y1=60x(0≤x≤10)
y2=-100x+600(0≤x≤6)
;
……………………………………………………………………2分,每个解析式1分
(2)当x=3时
y1=180
y2=300
∴y2-y1=120
当x=5时
y1=300
y2=100
∴y1-y2=200
当x=8时
y1=480
y2=0
∴y1-y2=y1=480
;………………5分每个1分
(3);S=
………………7分
(4)由题意得:S=200
①当0≤x≤时
-160x+600=200
∴x=
∴y1=60x=150km
②当≤x≤6时
160x-600=200
∴x=5
∴y1=300km
③当6≤x≤10时
60x≥360
不合题意
即:A加油站到甲地距离为150km或300km。……………………………8分
5
12.5
20
20
第3题
y
X
●
M
第2题
h
t
O
h
t
O
h
t
O
h
t
O
第9题
第10题
-
2
-
一
、选择题
(每小题3分,共30分)
1.下列函数(1),(2)
,(3)
,(4)
,(5)
中,是一次函数的有(
)
A.4个
B.3个
C.2个
D.1个
2.
如图,已知点在平面直角坐标系的位置,其坐标可能是(
)
A.(-1,2)
B.(1,2)
C.(-2,-1)
D.(1,-3)
3.
弹簧的长度与所挂物体的质量之间的关系式一次函数关系,图像如图所示,则弹簧本身的长度是
(
)
A.
B.
C.
D.
4.
如果在轴上,那么点的坐标是(
)
A.(-2,0)
B.(0,-2)
C.(1,0)
D.(0,1)
5.
某兴趣小组做实验,将一个装满水的啤酒瓶(上端细、下端粗)倒置,并设法使瓶里的水从瓶中匀速流出。那么该倒置啤酒瓶内水面高度随水流出的时间变化的图象大致是(
)
A
B
C
D
6.
已知一次函数与的图象在轴上相交于同一点,则的值是(
)
A.
B.
C.
D.
7.若,
,
则一次函数的图象不经过:
A.第一象限
B.第二象限
C.第三象限
D.第四象限
8.已知点,都在直线上,则
,大小关系是(
)
A.
B.
C.
D.不能比较
9.已知一次函数的图象如图所示,则的符号是(
)
A.
B.
C.
D.
10.
某学校组织团员举行申奥成功宣传活动,从学校骑车出发,先上坡到达地后,宣传8分钟;然后下坡到地宣传8分钟返回,行程情况如图.若返回时,上、下坡速度仍保持不变,在A地仍要宣传8分钟,那么他们从B地返回学校用的时间是(
)
A.45.2分钟
B.48分钟
C.46分钟
D.33分钟
二、填空题(每题3分,共12分)
11.
点(,),(2,)是一次函数图像上的两点,则 .(填“>”、“=”或“<”)
12.
直线与平行,且在轴上的截距是2,则该直线是
.
13.
已知为整数,且一次函数的图像不经过第二象限,则=
.
14.
某城市出租车收费按路程计算,3千米之内(包括3千米)收费6元,超过3千米每增加1千米加收1.6元,则车费(元)与路程(千米)之间的关系式为
______.
三、解答题(共58分)
15.
(10分)已知正比例函数y=mx的图象经过点(m,4),且y的值随着x值的增大而减小,求m的值.
16.(10分)在平面直角坐标系中,的边在轴上,且,点的坐标为(-5,0),点的坐标为(2,5)。
(1)求点坐标;(2)求的面积。
17.(10分)已知一次函数y=(3m-8)x+1-m图象与
y轴交点在x轴下方,且y随x的增大而减小,其中m为整数,求m的值
.
18.(10分)某电话公司开设了两种手机通讯业务,甲种业务:使用者先缴50元月租费,然后每通话1分钟,再付话费0.4元;乙种业务:不交月租费,每通话1分钟,付话费0.6元(指市话)。若一个月内通话x分钟,两种方式的费用分别为(元)和(元)。
(1)分别求出、与之间的函数关系式。
(2)根据每月可能的通话时间,作为消费者选用哪种缴费方式更实惠。
19.(10分)如图,直线的解析表达式为,且与轴交于点.直线经过点、,直线,交于点.
(1)求点的坐标;
(2)求直线的解析表达式;
(3)求的面积;
(4)在直线上存在异于点的另一个点,使得与的面积相等,求点的坐标。
20.
一辆客车从甲地开往甲地,一辆出租车从乙地开往甲地,两车同时出发,设客车离甲地的距离为y1(km),出租车离甲地的距离为y2(km),客车行驶时间为x(h),y1,y2与x的函数关系图象如图12所示:
(1)根据图象,直接写出y1,y2关于x的函数关系式。
(2)分别求出当x=3,x=5,x=8时,两车之间的距离。
(3)若设两车间的距离为S(km),请写出S关于x的函数关系式。
(4)甲、乙两地间有A、B两个加油站,相距200km,若客车进入A站加油时,出租车恰好进入B站加油。求A加油站到甲地的距离。
八年级上册《一次函数》章节测试
参考答案
选择题:(3分每题,共30分)
1、B
2、D
3、B
4、B
5、A
6、D
7、C
8、A
9、D
10、A
填空题:((3分每题,共12分)
11、;12、;13、;14、.
解答题:(共58分)
(10分)15.解:因为正比例函数y=mx的图象经过点(m,4),
所以4=m·m,解得m=±2……………………………………………..4分
又y的值随着x值的增大而减小,
所以m<0,故m=-2…………………………………………………….10分
(10分)16、(1)设点坐标为,因为,点的坐标为,
所以,解之得:,则点坐标为.……6分,每个坐标3分
(2).…………………………10分
17.m=2…………………………10分
18、(1)由题意可知:,.……………6分,每个3分
(2)假设甲种费用大于乙种费用,即:,则,得,所以当时,选择乙种业务更实惠;假设甲种费用等于乙种费用,即:,则,得,所以当时,两种业务都一样;假设甲种费用小于乙种费用,即:,则,得,所以当时,选择甲种业务更实惠。………10分
19、(1)由图像可设点坐标为,则,得,所以点坐标为.
……………………………………………………………………………………..…2分
(2)设直线的解析式为,有图像可知,得,所以直线的解析式为.………………..4分
(3)由题意得:,解得,所以点坐标为,又因为,所以.……………………7分
(4)设点坐标为,因为要使,即点到的距离也为,所以点坐标可写为,又因为点在直线上,则,得,所以点坐标是.…………10分
20.
(1)y1=60x(0≤x≤10)
y2=-100x+600(0≤x≤6)
;
……………………………………………………………………2分,每个解析式1分
(2)当x=3时
y1=180
y2=300
∴y2-y1=120
当x=5时
y1=300
y2=100
∴y1-y2=200
当x=8时
y1=480
y2=0
∴y1-y2=y1=480
;………………5分每个1分
(3);S=
………………7分
(4)由题意得:S=200
①当0≤x≤时
-160x+600=200
∴x=
∴y1=60x=150km
②当≤x≤6时
160x-600=200
∴x=5
∴y1=300km
③当6≤x≤10时
60x≥360
不合题意
即:A加油站到甲地距离为150km或300km。……………………………8分
5
12.5
20
20
第3题
y
X
●
M
第2题
h
t
O
h
t
O
h
t
O
h
t
O
第9题
第10题
-
2
-
