2021年新教材高中数学3.1.2第2课时分段函数 (word含解析)
文档属性
| 名称 | 2021年新教材高中数学3.1.2第2课时分段函数 (word含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 225.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-20 18:38:59 | ||
图片预览



文档简介
分段函数
(建议用时:40分钟)
基础练
一、选择题
1.设函数f(x)=则f(f(3))=( )
A.
B.3
C.
D.
2.函数f(x)=x+的图象是( )
A
B C D
3.函数f(x)=的值域是( )
A.R
B.[0,2]∪{3}
C.[0,+∞)
D.[0,3]
4.已知函数f(x)=若f(x)=3,则x的值是( )
A.
B.9
C.-1或1
D.-或
5.某单位为鼓励职工节约用水,作出了如下规定:每位职工每月用水量不超过10立方米的,按每立方米m元收费;用水量超过10立方米的,超过部分按每立方米2m元收费.某职工某月缴水费16m元,则该职工这个月实际用水量为
( )
A.13立方米
B.14立方米
C.18立方米
D.26立方米
二、填空题
6.已知f(x)=则f
+f
=________.
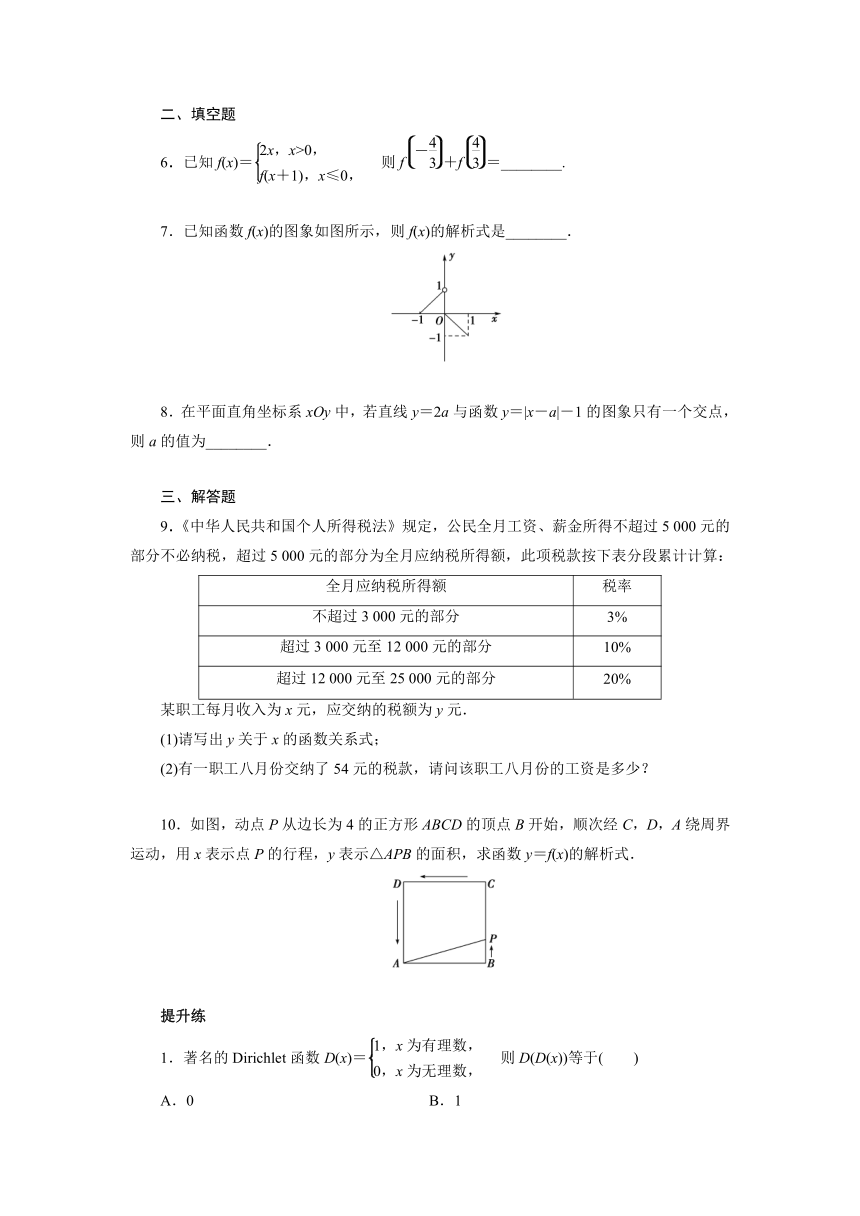
7.已知函数f(x)的图象如图所示,则f(x)的解析式是________.
8.在平面直角坐标系xOy中,若直线y=2a与函数y=|x-a|-1的图象只有一个交点,则a的值为________.
三、解答题
9.《中华人民共和国个人所得税法》规定,公民全月工资、薪金所得不超过5
000元的部分不必纳税,超过5
000元的部分为全月应纳税所得额,此项税款按下表分段累计计算:
全月应纳税所得额
税率
不超过3
000元的部分
3%
超过3
000元至12
000元的部分
10%
超过12
000元至25
000元的部分
20%
某职工每月收入为x元,应交纳的税额为y元.
(1)请写出y关于x的函数关系式;
(2)有一职工八月份交纳了54元的税款,请问该职工八月份的工资是多少?
10.如图,动点P从边长为4的正方形ABCD的顶点B开始,顺次经C,D,A绕周界运动,用x表示点P的行程,y表示△APB的面积,求函数y=f(x)的解析式.
提升练
1.著名的Dirichlet函数D(x)=则D(D(x))等于( )
A.0
B.1
C.
D.
2.(多选)已知函数f(x)=关于函数f(x)的结论正确的是
( )
A.f(x)的值域为(-∞,4)
B.f(1)=3
C.若f(x)=3,则x的值是
D.f(x)<1的解集为(-1,1)
3.已知实数a≠0,函数f(x)=若f(1-a)=f(1+a),则a的值为________.
4.若定义运算a⊙b=则函数f(x)=x⊙(2-x)的解析式为________,值域为________.
拓展
已知函数f(x)=|x+1|+|x-2|,g(x)=|x-3|.
(1)在平面直角坐标系里作出f(x),g(x)的图象;
(2)?x∈R,用min(x)表示f(x),g(x)中的较小者,记作min(x)={f(x),g(x)},请用图象法和解析法表示min(x);
(3)求满足f(x)>g(x)的x的取值范围.
参考答案:
基础练
一、选择题
1.设函数f(x)=则f(f(3))=( )
A.
B.3
C.
D.
D [∵f(3)=≤1,
∴f(f(3))=2+1=.]
2.函数f(x)=x+的图象是( )
A
B C D
C [当x>0时,f(x)=x+=x+1,
当x<0时,f(x)=x-1,且x≠0,
根据一次函数图象可知C正确.
故选C.]
3.函数f(x)=的值域是( )
A.R
B.[0,2]∪{3}
C.[0,+∞)
D.[0,3]
B [当0≤x≤1时,0≤2x≤2,即0≤f(x)≤2;当14.已知函数f(x)=若f(x)=3,则x的值是( )
A.
B.9
C.-1或1
D.-或
A [依题意,若x≤0,则x+2=3,解得x=1,不合题意,舍去.若05.某单位为鼓励职工节约用水,作出了如下规定:每位职工每月用水量不超过10立方米的,按每立方米m元收费;用水量超过10立方米的,超过部分按每立方米2m元收费.某职工某月缴水费16m元,则该职工这个月实际用水量为
( )
A.13立方米
B.14立方米
C.18立方米
D.26立方米
A [该单位职工每月应缴水费y与实际用水量x满足的关系式为y=由y=16m,可知x>10.令2mx-10m=16m,解得x=13.]
二、填空题
6.已知f(x)=则f
+f
=________.
4 [∵f
=f
=f
=f
=f
=2×=,
f
=2×=,
∴f
+f
=+==4.]
7.已知函数f(x)的图象如图所示,则f(x)的解析式是________.
f(x)= [由题图可知,图象是由两条线段组成,
当-1≤x<0时,设f(x)=ax+b,将(-1,0),(0,1)代入解析式,则∴即f(x)=x+1.
当0≤x≤1时,设f(x)=kx,将(1,-1)代入,则k=-1,即f(x)=-x.
综上,f(x)=]
8.在平面直角坐标系xOy中,若直线y=2a与函数y=|x-a|-1的图象只有一个交点,则a的值为________.
- [在同一平面直角坐标系内,作出函数y=2a与y=|x-a|-1的大致图象,如图所示.
由题意,可知2a=-1,则a=-.]
三、解答题
9.《中华人民共和国个人所得税法》规定,公民全月工资、薪金所得不超过5
000元的部分不必纳税,超过5
000元的部分为全月应纳税所得额,此项税款按下表分段累计计算:
全月应纳税所得额
税率
不超过3
000元的部分
3%
超过3
000元至12
000元的部分
10%
超过12
000元至25
000元的部分
20%
某职工每月收入为x元,应交纳的税额为y元.
(1)请写出y关于x的函数关系式;
(2)有一职工八月份交纳了54元的税款,请问该职工八月份的工资是多少?
[解] (1)由题意,得
y=
(2)∵该职工八月份交纳了54元的税款,
∴5
000000,(x-5
000)×3%=54,
解得x=6
800.
故这名职工八月份的工资是6
800元.
10.如图,动点P从边长为4的正方形ABCD的顶点B开始,顺次经C,D,A绕周界运动,用x表示点P的行程,y表示△APB的面积,求函数y=f(x)的解析式.
[解] 当点P在BC上运动,即0≤x≤4时,y=×4×x=2x;
当点P在CD上运动,即4当点P在DA上运动,即8综上可知,f(x)=
提升练
1.著名的Dirichlet函数D(x)=则D(D(x))等于( )
A.0
B.1
C.
D.
B [当x为无理数时D(x)=0,∴D(D(x))=D(0)=1;
当x为有理数时,D(x)=1,∴D(D(x))=D(1)=1.
综上可知B正确.]
2.(多选)已知函数f(x)=关于函数f(x)的结论正确的是
( )
A.f(x)的值域为(-∞,4)
B.f(1)=3
C.若f(x)=3,则x的值是
D.f(x)<1的解集为(-1,1)
AC [当x≤-1时,f(x)的取值范围是(-∞,1],当-13.已知实数a≠0,函数f(x)=若f(1-a)=f(1+a),则a的值为________.
- [当a>0时,1-a<1,1+a>1,∴2(1-a)+a=-1-a-2a,解得a=-(舍去).
当a<0时,1-a>1,1+a<1,∴-1+a-2a=2+2a+a,解得a=-.]
4.若定义运算a⊙b=则函数f(x)=x⊙(2-x)的解析式为________,值域为________.
f(x)= (-∞,1] [由题意可知,f(x)=
画出函数f(x)的图象得值域为(-∞,1].
]
拓展
已知函数f(x)=|x+1|+|x-2|,g(x)=|x-3|.
(1)在平面直角坐标系里作出f(x),g(x)的图象;
(2)?x∈R,用min(x)表示f(x),g(x)中的较小者,记作min(x)={f(x),g(x)},请用图象法和解析法表示min(x);
(3)求满足f(x)>g(x)的x的取值范围.
[解] (1)f(x)=g(x)=
则对应的图象如图:
(2)min(x)图象如图:
解析式为min(x)=
(3)若f(x)>g(x),
则由图象知在A点左侧,B点右侧满足条件.
此时对应的x满足x>0或x<-2,
即不等式f(x)>g(x)的解集为(-∞,-2)∪(0,+∞).
(建议用时:40分钟)
基础练
一、选择题
1.设函数f(x)=则f(f(3))=( )
A.
B.3
C.
D.
2.函数f(x)=x+的图象是( )
A
B C D
3.函数f(x)=的值域是( )
A.R
B.[0,2]∪{3}
C.[0,+∞)
D.[0,3]
4.已知函数f(x)=若f(x)=3,则x的值是( )
A.
B.9
C.-1或1
D.-或
5.某单位为鼓励职工节约用水,作出了如下规定:每位职工每月用水量不超过10立方米的,按每立方米m元收费;用水量超过10立方米的,超过部分按每立方米2m元收费.某职工某月缴水费16m元,则该职工这个月实际用水量为
( )
A.13立方米
B.14立方米
C.18立方米
D.26立方米
二、填空题
6.已知f(x)=则f
+f
=________.
7.已知函数f(x)的图象如图所示,则f(x)的解析式是________.
8.在平面直角坐标系xOy中,若直线y=2a与函数y=|x-a|-1的图象只有一个交点,则a的值为________.
三、解答题
9.《中华人民共和国个人所得税法》规定,公民全月工资、薪金所得不超过5
000元的部分不必纳税,超过5
000元的部分为全月应纳税所得额,此项税款按下表分段累计计算:
全月应纳税所得额
税率
不超过3
000元的部分
3%
超过3
000元至12
000元的部分
10%
超过12
000元至25
000元的部分
20%
某职工每月收入为x元,应交纳的税额为y元.
(1)请写出y关于x的函数关系式;
(2)有一职工八月份交纳了54元的税款,请问该职工八月份的工资是多少?
10.如图,动点P从边长为4的正方形ABCD的顶点B开始,顺次经C,D,A绕周界运动,用x表示点P的行程,y表示△APB的面积,求函数y=f(x)的解析式.
提升练
1.著名的Dirichlet函数D(x)=则D(D(x))等于( )
A.0
B.1
C.
D.
2.(多选)已知函数f(x)=关于函数f(x)的结论正确的是
( )
A.f(x)的值域为(-∞,4)
B.f(1)=3
C.若f(x)=3,则x的值是
D.f(x)<1的解集为(-1,1)
3.已知实数a≠0,函数f(x)=若f(1-a)=f(1+a),则a的值为________.
4.若定义运算a⊙b=则函数f(x)=x⊙(2-x)的解析式为________,值域为________.
拓展
已知函数f(x)=|x+1|+|x-2|,g(x)=|x-3|.
(1)在平面直角坐标系里作出f(x),g(x)的图象;
(2)?x∈R,用min(x)表示f(x),g(x)中的较小者,记作min(x)={f(x),g(x)},请用图象法和解析法表示min(x);
(3)求满足f(x)>g(x)的x的取值范围.
参考答案:
基础练
一、选择题
1.设函数f(x)=则f(f(3))=( )
A.
B.3
C.
D.
D [∵f(3)=≤1,
∴f(f(3))=2+1=.]
2.函数f(x)=x+的图象是( )
A
B C D
C [当x>0时,f(x)=x+=x+1,
当x<0时,f(x)=x-1,且x≠0,
根据一次函数图象可知C正确.
故选C.]
3.函数f(x)=的值域是( )
A.R
B.[0,2]∪{3}
C.[0,+∞)
D.[0,3]
B [当0≤x≤1时,0≤2x≤2,即0≤f(x)≤2;当1
A.
B.9
C.-1或1
D.-或
A [依题意,若x≤0,则x+2=3,解得x=1,不合题意,舍去.若0
( )
A.13立方米
B.14立方米
C.18立方米
D.26立方米
A [该单位职工每月应缴水费y与实际用水量x满足的关系式为y=由y=16m,可知x>10.令2mx-10m=16m,解得x=13.]
二、填空题
6.已知f(x)=则f
+f
=________.
4 [∵f
=f
=f
=f
=f
=2×=,
f
=2×=,
∴f
+f
=+==4.]
7.已知函数f(x)的图象如图所示,则f(x)的解析式是________.
f(x)= [由题图可知,图象是由两条线段组成,
当-1≤x<0时,设f(x)=ax+b,将(-1,0),(0,1)代入解析式,则∴即f(x)=x+1.
当0≤x≤1时,设f(x)=kx,将(1,-1)代入,则k=-1,即f(x)=-x.
综上,f(x)=]
8.在平面直角坐标系xOy中,若直线y=2a与函数y=|x-a|-1的图象只有一个交点,则a的值为________.
- [在同一平面直角坐标系内,作出函数y=2a与y=|x-a|-1的大致图象,如图所示.
由题意,可知2a=-1,则a=-.]
三、解答题
9.《中华人民共和国个人所得税法》规定,公民全月工资、薪金所得不超过5
000元的部分不必纳税,超过5
000元的部分为全月应纳税所得额,此项税款按下表分段累计计算:
全月应纳税所得额
税率
不超过3
000元的部分
3%
超过3
000元至12
000元的部分
10%
超过12
000元至25
000元的部分
20%
某职工每月收入为x元,应交纳的税额为y元.
(1)请写出y关于x的函数关系式;
(2)有一职工八月份交纳了54元的税款,请问该职工八月份的工资是多少?
[解] (1)由题意,得
y=
(2)∵该职工八月份交纳了54元的税款,
∴5
000
000)×3%=54,
解得x=6
800.
故这名职工八月份的工资是6
800元.
10.如图,动点P从边长为4的正方形ABCD的顶点B开始,顺次经C,D,A绕周界运动,用x表示点P的行程,y表示△APB的面积,求函数y=f(x)的解析式.
[解] 当点P在BC上运动,即0≤x≤4时,y=×4×x=2x;
当点P在CD上运动,即4
提升练
1.著名的Dirichlet函数D(x)=则D(D(x))等于( )
A.0
B.1
C.
D.
B [当x为无理数时D(x)=0,∴D(D(x))=D(0)=1;
当x为有理数时,D(x)=1,∴D(D(x))=D(1)=1.
综上可知B正确.]
2.(多选)已知函数f(x)=关于函数f(x)的结论正确的是
( )
A.f(x)的值域为(-∞,4)
B.f(1)=3
C.若f(x)=3,则x的值是
D.f(x)<1的解集为(-1,1)
AC [当x≤-1时,f(x)的取值范围是(-∞,1],当-1
- [当a>0时,1-a<1,1+a>1,∴2(1-a)+a=-1-a-2a,解得a=-(舍去).
当a<0时,1-a>1,1+a<1,∴-1+a-2a=2+2a+a,解得a=-.]
4.若定义运算a⊙b=则函数f(x)=x⊙(2-x)的解析式为________,值域为________.
f(x)= (-∞,1] [由题意可知,f(x)=
画出函数f(x)的图象得值域为(-∞,1].
]
拓展
已知函数f(x)=|x+1|+|x-2|,g(x)=|x-3|.
(1)在平面直角坐标系里作出f(x),g(x)的图象;
(2)?x∈R,用min(x)表示f(x),g(x)中的较小者,记作min(x)={f(x),g(x)},请用图象法和解析法表示min(x);
(3)求满足f(x)>g(x)的x的取值范围.
[解] (1)f(x)=g(x)=
则对应的图象如图:
(2)min(x)图象如图:
解析式为min(x)=
(3)若f(x)>g(x),
则由图象知在A点左侧,B点右侧满足条件.
此时对应的x满足x>0或x<-2,
即不等式f(x)>g(x)的解集为(-∞,-2)∪(0,+∞).
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
