2020-2021学年安徽省合肥市长丰县九年级(上)期末数学试卷(Word版 含解析)
文档属性
| 名称 | 2020-2021学年安徽省合肥市长丰县九年级(上)期末数学试卷(Word版 含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-19 06:27:44 | ||
图片预览



文档简介
2020-2021学年安徽省合肥市长丰县九年级第一学期期末数学试卷
一、选择题(共10小题,每小题4分,满分40分)
1.计算:tan45°的结果是( )
A.
B.1
C.
D.
2.抛物线y=﹣3x2+2的顶点坐标为( )
A.(0,0)
B.(﹣3,﹣2)
C.(﹣3,2)
D.(0,2)
3.下列反比例函数图象的一个分支在第三象限的是( )
A.
B.
C.
D.
4.在一张缩印出来的纸上,一个三角形的一条边由原图中的6cm变成了2cm,则缩印出的三角形的周长是原图中三角形周长的( )
A.
B.
C.
D.
5.如图,双曲线y1=与直线y2=ax相交于A,B两点,点A的坐标为(2,m),若y1<y2,则x的取值范围是( )
A.x>2或﹣1<x<0
B.﹣2<x<0或0<x<2
C.x>2或﹣2<x<0
D.x<﹣2或0<x<2
6.某同学在利用描点法画二次函数y=ax2+bx+c(a≠0)的图象时,先取自变量x的一些值,计算出相应的函数值y,如下表所示:
x
…
0
1
2
3
4
…
y
…
﹣3
0
﹣1
0
3
…
接着,他在描点时发现,表格中有一组数据计算错误,他计算错误的一组数据是( )
A.
B.
C.
D.
7.如图,△OAB与△OCD是以点O为位似中心的位似图形,相似比为1:2,∠OCD=90°,CO=CD.若B(1,0),则点C的坐标为( )
A.(1,2)
B.(1,1)
C.(,)
D.(2,1)
8.如图,乐器上的一根弦AB=80cm,两个端点A,B固定在乐器板面上,支撑点C是靠近点B的黄金分割点,支撑点D是靠近点A的黄金分割点,则C,D之间的距离为( )
A.(40﹣40)cm
B.(80﹣40)cm
C.(120﹣40)cm
D.(80﹣160)cm
9.如图,在△ABC中,∠BAC=120°,AC=6,AB=4,则BC的长是( )
A.6
B.2
C.2
D.9
10.已知函数y=ax2+bx+c,当y>0时,.则函数y=cx2﹣bx+a的图象可能是下图中的( )
A.
B.
C.
D.
二、填空题(本大题共4小题,每小题5分,满分20分)
11.如果2x=5y(y≠0),那么=
.
12.在Rt△ABC中,∠C=90°,AC=5,BC=12,则sinA=
.
13.已知二次函数y=ax2﹣2x+1的图象与x轴只有一个公共点,则a的值是
.
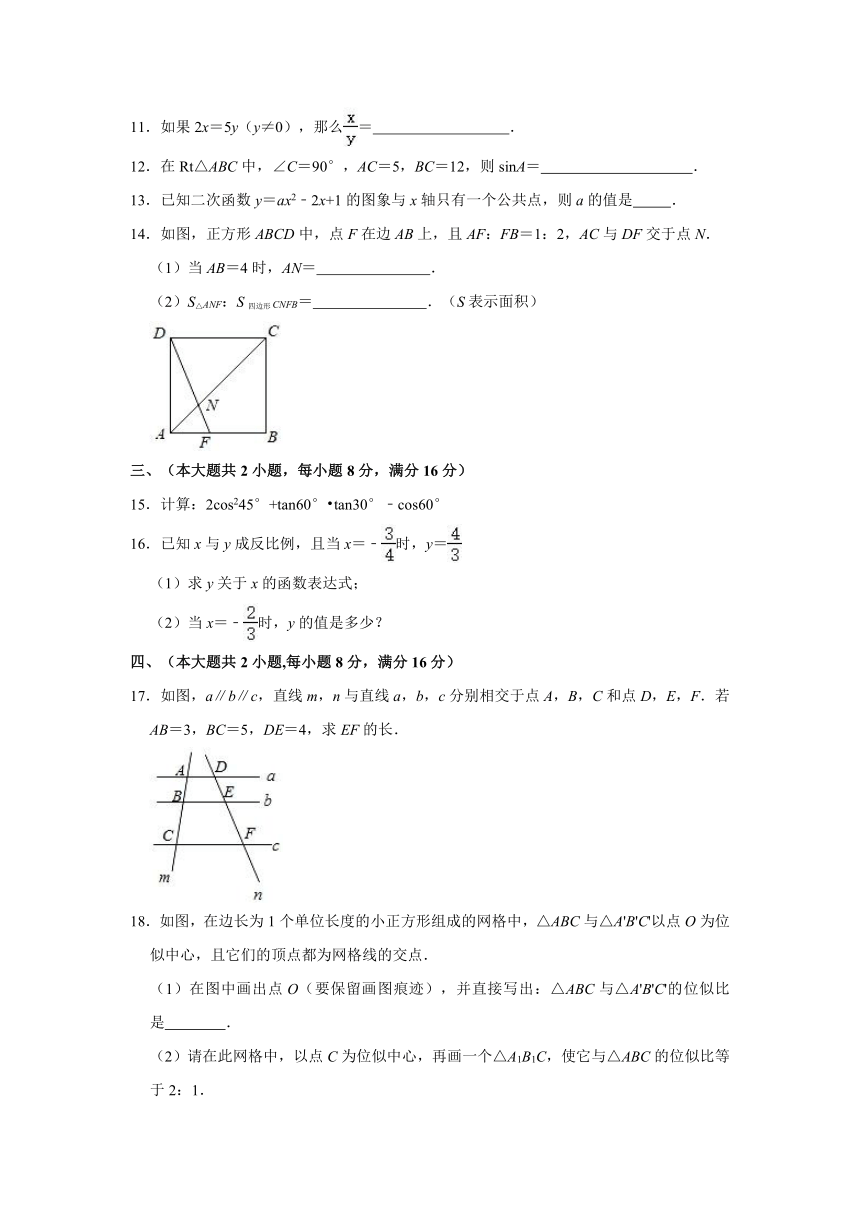
14.如图,正方形ABCD中,点F在边AB上,且AF:FB=1:2,AC与DF交于点N.
(1)当AB=4时,AN=
.
(2)S△ANF:S四边形CNFB=
.(S表示面积)
三、(本大题共2小题,每小题8分,满分16分)
15.计算:2cos245°+tan60°?tan30°﹣cos60°
16.已知x与y成反比例,且当x=﹣时,y=
(1)求y关于x的函数表达式;
(2)当x=﹣时,y的值是多少?
四、(本大题共2小题,每小题8分,满分16分)
17.如图,a∥b∥c,直线m,n与直线a,b,c分别相交于点A,B,C和点D,E,F.若AB=3,BC=5,DE=4,求EF的长.
18.如图,在边长为1个单位长度的小正方形组成的网格中,△ABC与△A'B'C'以点O为位似中心,且它们的顶点都为网格线的交点.
(1)在图中画出点O(要保留画图痕迹),并直接写出:△ABC与△A'B'C'的位似比是
.
(2)请在此网格中,以点C为位似中心,再画一个△A1B1C,使它与△ABC的位似比等于2:1.
五、(本大题共2小题,每小题10分,满分20分)
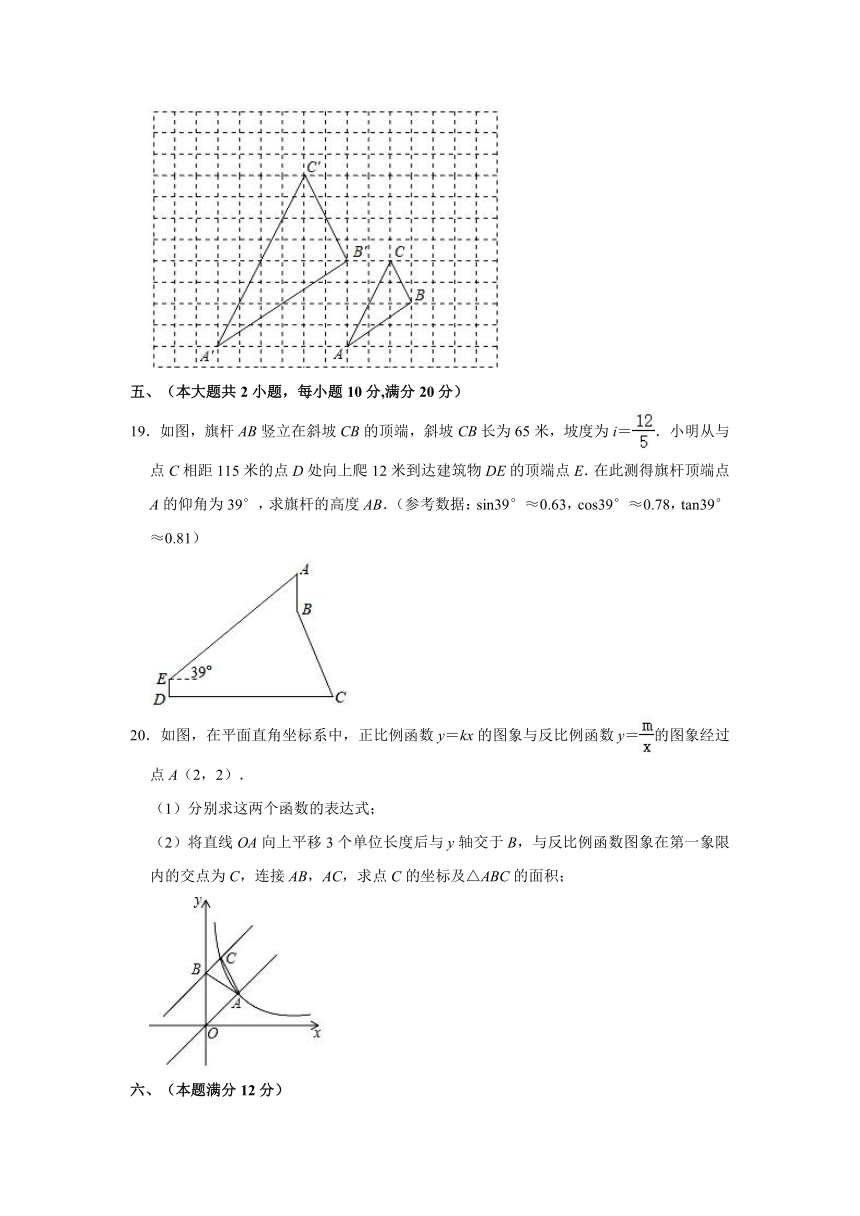
19.如图,旗杆AB竖立在斜坡CB的顶端,斜坡CB长为65米,坡度为i=.小明从与点C相距115米的点D处向上爬12米到达建筑物DE的顶端点E.在此测得旗杆顶端点A的仰角为39°,求旗杆的高度AB.(参考数据:sin39°≈0.63,cos39°≈0.78,tan39°≈0.81)
20.如图,在平面直角坐标系中,正比例函数y=kx的图象与反比例函数y=的图象经过点A(2,2).
(1)分别求这两个函数的表达式;
(2)将直线OA向上平移3个单位长度后与y轴交于B,与反比例函数图象在第一象限内的交点为C,连接AB,AC,求点C的坐标及△ABC的面积;
六、(本题满分12分)
21.如图.在△ABC中.AB=4,D是AB上的一点(不与点A,B重合),过点D作DE∥BC,交AC于点E.连接DC,设△ABC的面积为S,△DEC的面积为S′.
(1)当D是AB的中点时,直接写出=
.
(2)若AD=x,=y,求y关于x的函数关系式以及自变量x的取值范围.
七、(本题满分12分)
22.网络直播销售已经成为一种热门的销售方式,某生产商在一销售平台上进行直播销售板栗.已知板栗的成本价为6元/kg,每日销售量y(kg)与销售单价x(元/kg)满足一次函数关系,下表记录的是有关数据,经销售发现,销售单价不低于成本价且不高于30元/kg.设公司销售板栗的日获利为w(元).
x(元/kg)
7
8
9
y(kg)
4300
4200
4100
(1)直接写出日销售量y与销售单价x之间的函数关系式为
;(不用写自变量的取值范围)
(2)当销售单价定为多少时,销售这种板栗日获利w最大?最大利润为多少元?
(3)当销售单价在什么范围内时,日获利w不低于42000元?
八、(本题满分14分)
23.如图,在边长为2的菱形ABCD中,∠C=60°,E是边BC的中点,连接DE,AE.
(1)直接写出DE的长为
.
(2)F为边CD上的一点,连接AF,交DE于点G,连接EF,若AF⊥EF.
①求证:△AGE∽△DGF.
②求DF的长.
参考答案
一、选择题(本大题共10小题,每小题4分,满分40分)
1.计算:tan45°的结果是( )
A.
B.1
C.
D.
【分析】根据我们记忆的特殊角的三角函数值即可得出答案.
解:tan45°=1.
故选:B.
2.抛物线y=﹣3x2+2的顶点坐标为( )
A.(0,0)
B.(﹣3,﹣2)
C.(﹣3,2)
D.(0,2)
【分析】由抛物线顶点式y=a(x﹣h)2+k的顶点坐标为(h,k),直接得到答案.
解:抛物线y=﹣3x2+2的顶点坐标为(0,2),
故选:D.
3.下列反比例函数图象的一个分支在第三象限的是( )
A.
B.
C.
D.
【分析】当k>0,双曲线的两支分别位于第一、第三象限,在每一象限内y随x的增大而减小,依据反比例函数的性质进行判断即可.
解:A.y=图象位于第二、四象限,不合题意;
B.y=图象位于第一、三象限,符合题意;
C.y=图象不一定位于第一、三象限,不合题意;
D.y=图象位于第二、四象限,不合题意;
故选:B.
4.在一张缩印出来的纸上,一个三角形的一条边由原图中的6cm变成了2cm,则缩印出的三角形的周长是原图中三角形周长的( )
A.
B.
C.
D.
【分析】根据相似三角形的周长比等于相似比计算,得到答案.
解:∵三角形的一条边由原图中的6cm变成了2cm,
∴原三角形与缩印出的三角形是相似比为3:1,
∴原三角形与缩印出的三角形的周长比为3:1,
∴缩印出的三角形的周长是原图中三角形周长的,
故选:A.
5.如图,双曲线y1=与直线y2=ax相交于A,B两点,点A的坐标为(2,m),若y1<y2,则x的取值范围是( )
A.x>2或﹣1<x<0
B.﹣2<x<0或0<x<2
C.x>2或﹣2<x<0
D.x<﹣2或0<x<2
【分析】根据反比例函数和正比例函数的对称性求得B(﹣2,﹣m),然后根据函数图象的上下位置关系结合交点的横坐标,即可得出不等式y1<y2的解集.
解:∵双曲线y1=与直线y2=ax相交于A,B两点,点的坐标为(2,m),
∴B(﹣2,﹣m),
又∵y1<y2,
∴x的取值范围是﹣2<x<0或x>2.
故选:C.
6.某同学在利用描点法画二次函数y=ax2+bx+c(a≠0)的图象时,先取自变量x的一些值,计算出相应的函数值y,如下表所示:
x
…
0
1
2
3
4
…
y
…
﹣3
0
﹣1
0
3
…
接着,他在描点时发现,表格中有一组数据计算错误,他计算错误的一组数据是( )
A.
B.
C.
D.
【分析】利用表中数据和二次函数的性质得到抛物线的对称轴为直线x=2,则顶点坐标为(2,﹣1),于是可判断抛物线的开口向上,则x=0和x=4的函数值相等且大于0,然后可判断A选项错误.
解:∵x=1和x=3时,y=0;
∴抛物线的对称轴为直线x=2,
∴顶点坐标为(2,﹣1),
∴抛物线的开口向上,
∴x=0和x=4的函数值相等且大于0,
∴x=0,y=﹣3错误.
故选:A.
7.如图,△OAB与△OCD是以点O为位似中心的位似图形,相似比为1:2,∠OCD=90°,CO=CD.若B(1,0),则点C的坐标为( )
A.(1,2)
B.(1,1)
C.(,)
D.(2,1)
【分析】首先利用等腰直角三角形的性质得出A点坐标,再利用位似是特殊的相似,若两个图形△ABC和△A′B′C′以原点为位似中心,相似比是k,△ABC上一点的坐标是(x,y),则在△A′B′C′中,它的对应点的坐标是(kx,ky)或(﹣kx,ky),进而求出即可.
解:∵∠OAB=∠OCD=90°,AO=AB,CO=CD,等腰Rt△OAB与等腰Rt△OCD是位似图形,点B的坐标为(1,0),
∴BO=1,则AO=AB=,
∴A(,),
∵等腰Rt△OAB与等腰Rt△OCD是位似图形,O为位似中心,相似比为1:2,
∴点C的坐标为:(1,1).
故选:B.
8.如图,乐器上的一根弦AB=80cm,两个端点A,B固定在乐器板面上,支撑点C是靠近点B的黄金分割点,支撑点D是靠近点A的黄金分割点,则C,D之间的距离为( )
A.(40﹣40)cm
B.(80﹣40)cm
C.(120﹣40)cm
D.(80﹣160)cm
【分析】根据黄金分割的概念和黄金比值求出AC=BD=40﹣40,进而得出答案.
解:∵点C是靠近点B的黄金分割点,点D是靠近点A的黄金分割点,
∴AC=BD=80×=40﹣40,
∴CD=BD﹣(AB﹣BD)=2BD﹣AB=80﹣160,
故选:D.
9.如图,在△ABC中,∠BAC=120°,AC=6,AB=4,则BC的长是( )
A.6
B.2
C.2
D.9
【分析】作CD⊥AB,根据直角三角形的性质求出AD,根据勾股定理求出CD,根据勾股定理计算,得到答案.
解:过点C作CD⊥AB,交BA的延长线于点D,
∵∠BAC=120°,
∴∠DAC=180°﹣120°=60°,
∴∠ACD=30°,
∴AD=AC=3,
∴BD=AB+AD=7,
由勾股定理得,CD==3,
在Rt△BCD中,BC==2,
故选:B.
10.已知函数y=ax2+bx+c,当y>0时,.则函数y=cx2﹣bx+a的图象可能是下图中的( )
A.
B.
C.
D.
【分析】当y>0时,,所以可判断a<0,可知﹣=﹣+=﹣,=﹣×=﹣,所以可知a=6b,a=﹣6c,则b=﹣c,不妨设c=1进而得出解析式,找出符合要求的答案.
解:因为函数y=ax2+bx+c,当y>0时,
所以可判断a<0,可知﹣=﹣+=﹣,=﹣×=﹣
所以可知a=6b,a=﹣6c,则b=﹣c,不妨设c=1
则函数y=cx2﹣bx+a为函数y=x2+x﹣6
即y=(x﹣2)(x+3)
则可判断与x轴的交点坐标是(2,0),(﹣3,0),
故选:A.
二、填空题(本大题共4小题,每小题5分,满分20分)
11.如果2x=5y(y≠0),那么= .
【分析】根据比例的性质直接求解即可.
解:∵2x=5y(y≠0),
∴=.
故答案为:.
12.在Rt△ABC中,∠C=90°,AC=5,BC=12,则sinA= .
【分析】根据题意画出图形,进而利用勾股定理得出AB的长,再利用锐角三角函数关系,即可得出答案.
解:如图所示:∵∠C=90°,AC=5,BC=12,
∴AB==13,
∴sinA=.
故答案为:.
13.已知二次函数y=ax2﹣2x+1的图象与x轴只有一个公共点,则a的值是 1 .
【分析】由抛物线y=ax2+bx+c与x轴只有一个公共点,得到b2﹣4ac=0,即可求出a的值.
解:∵二次函数y=ax2﹣2x+1的图象与x轴只有一个公共点,
∴b2﹣4ac=4﹣4a=0,
∴a=1,
故答案为1.
14.如图,正方形ABCD中,点F在边AB上,且AF:FB=1:2,AC与DF交于点N.
(1)当AB=4时,AN= .
(2)S△ANF:S四边形CNFB= 1:11 .(S表示面积)
【分析】(1)根据正方形的性质得到AB∥CD,从而推出△AFN∽△CDN,利用相似三角形的性质得到,结合图形根据线段之间的和差关系推出=,进而根据正方形的性质、线段之间的和差关系和比例关系求解即可;
(2)根据相似三角形的性质推出S△CDN=9S△AFN,根据线段的比例关系推出S△ADN=3S△AFN,从而结合图形推出S四边形CNFB=11S△AFN,进行求解即可.
解:(1)∵四边形ABCD是正方形,
∴AB=CD,AB∥CD,
∴△AFN∽△CDN,
∴,
∵AF:FB=1:2,AF+BF=AB,
∴AF:AB=1:3,
∴=,
∵AB=4,AC是正方形ABCD的对角线,
∴AC=4,
又AN+CN=AC,
∴AN=AC=,
故答案为:;
(2)由(1)得△AFN∽△CDN,且AN:CN=1:3,
∴S△AFN:S△CDN=1:9,
∴S△CDN=9S△AFN,
又FN:DN=1:3,
∴S△AFN:S△ADN=1:3,
∴S△ADN=3S△AFN,
∴S△ABC=S△ADC=S△CDN+S△ADN=12S△AFN,
∴S四边形CNFB=S△ABC﹣S△AFN=11S△AFN,
∴S△ANF:S四边形CNFB=1:11,
故答案为:1:11.
三、(本大题共2小题,每小题8分,满分16分)
15.计算:2cos245°+tan60°?tan30°﹣cos60°
【分析】把特殊角的三角函数值代入计算,得到答案.
解:原式=2×()2+×﹣
=1+1﹣
=.
16.已知x与y成反比例,且当x=﹣时,y=
(1)求y关于x的函数表达式;
(2)当x=﹣时,y的值是多少?
【分析】(1)设xy=k(k为常数,k≠0),把x与y的值代入求出k的值,即可确定出解析式;
(2)把x的值代入解析式求出y的值即可.
解:(1)∵x与y成反比例,
∴可设xy=k(k为常数,k≠0),
∵当x=﹣时,y=,
∴解得k=﹣1,
所以y关于x的表达式y=﹣;
(2)当x=﹣时,y=.
四、(本大题共2小题,每小题8分,满分16分)
17.如图,a∥b∥c,直线m,n与直线a,b,c分别相交于点A,B,C和点D,E,F.若AB=3,BC=5,DE=4,求EF的长.
【分析】根据平行线分线段成比例定理,列出比例式求解即可得到答案.
解:∵a∥b∥c,
∴,
即,
解得:EF=.
18.如图,在边长为1个单位长度的小正方形组成的网格中,△ABC与△A'B'C'以点O为位似中心,且它们的顶点都为网格线的交点.
(1)在图中画出点O(要保留画图痕迹),并直接写出:△ABC与△A'B'C'的位似比是 1:2 .
(2)请在此网格中,以点C为位似中心,再画一个△A1B1C,使它与△ABC的位似比等于2:1.
【分析】(1)直接利用位似图形的性质得出位似中心的位置;
(2)直接利用位似比得出对应点位置进而得出答案.
解:(1)如图所示:点O即为所求,△ABC与△A'B'C'的位似比是:1;2;
故答案为:1:2;
(2)如图所示:△A1B1C即为所求.
五、(本大题共2小题,每小题10分,满分20分)
19.如图,旗杆AB竖立在斜坡CB的顶端,斜坡CB长为65米,坡度为i=.小明从与点C相距115米的点D处向上爬12米到达建筑物DE的顶端点E.在此测得旗杆顶端点A的仰角为39°,求旗杆的高度AB.(参考数据:sin39°≈0.63,cos39°≈0.78,tan39°≈0.81)
【分析】过点B作BF⊥CD,垂足为F,过点E作EG⊥BF,垂足为G,通过作高,构造直角三角形,利用直角三角形的边角关系和坡度即可求出答案.
解:过点B作BF⊥CD,垂足为F,过点E作EG⊥BF,垂足为G,
在Rt△BCF中,
由斜坡BC的坡度i=,
得,=,
∵BC=65米,
设BF=12x(米),FC=5x(米),
由勾股定理得,(12x)2+(5x)2=652,
∴x=5,
∴BF=60米,FC=25米,
∵DC=115米,
∴DF=DC﹣FC=115﹣25=90(米)=EG,
在Rt△AEG中,AG=EG?tan39°≈90×0.81=72.9(米),
∴AB=AG+FG﹣BF=72.9+12﹣60=24.9(米),
答:旗杆的高度AB为24.9米.
20.如图,在平面直角坐标系中,正比例函数y=kx的图象与反比例函数y=的图象经过点A(2,2).
(1)分别求这两个函数的表达式;
(2)将直线OA向上平移3个单位长度后与y轴交于B,与反比例函数图象在第一象限内的交点为C,连接AB,AC,求点C的坐标及△ABC的面积;
【分析】(1)把A点坐标分别代入y=kx和y=中分别求出k、m即可;
(2)利用直线平移的规律得到直线BC的解析式为y=x+3,则B(0,3)再解方程组得点C的坐标为(1,4);连接OC,根据三角形面积公式,利用S△ABC=S△OBC进行计算.
解:(1)把A(2,2)代入y=kx得2k=2,解得k=1;
把A(2,2)代入y=得m=2×2=4,
∴正比例函数的解析式为y=x;反比例函数的解析式为y=;
(2)直线y=x向上平移3的单位得到直线BC的解析式为y=x+3,
当x=0时,y=x+3=3,则B(0,3),
解方程组得或,
∴点C的坐标为(1,4);
连接OC,
S△ABC=S△OBC=×3×1=.
六、(本题满分12分)
21.如图.在△ABC中.AB=4,D是AB上的一点(不与点A,B重合),过点D作DE∥BC,交AC于点E.连接DC,设△ABC的面积为S,△DEC的面积为S′.
(1)当D是AB的中点时,直接写出= .
(2)若AD=x,=y,求y关于x的函数关系式以及自变量x的取值范围.
【分析】(1)先根据DE∥BC推△ADE∽△ABC,再进一步推=,再根据△ADE与△CED等底同高,求S△ADE=S△CED,等量代换最后求出;
(2)求==①,再求=②,①÷②得最后结果.
解:(1)∵DE∥BC,
∴△ADE∽△ABC,
∴=,
∵D是AB的中点,
∴DE是△ABC的中位线,
∴=,AE=EC
∴=,
∵△ADE与△CED等底同高,
∴S△ADE=S△CED,
∵设△ABC的面积为S,△DEC的面积为S′,
∴=.
故答案为:.
(2)∵AB=4,AD=x,DE∥BC,
∴△ADE∽△ABC
∴==①,
=,
∴=,
∵△ADE与△CEDD,AE、EC边同高,
∴=②,
∴①÷②得,
∵设△ABC的面积为S,△DEC的面积为S′,=y,
∴y=﹣x2+x,
∵AB=4,
∴自变量x的取值范围是0<x<4.
七、(本题满分12分)
22.网络直播销售已经成为一种热门的销售方式,某生产商在一销售平台上进行直播销售板栗.已知板栗的成本价为6元/kg,每日销售量y(kg)与销售单价x(元/kg)满足一次函数关系,下表记录的是有关数据,经销售发现,销售单价不低于成本价且不高于30元/kg.设公司销售板栗的日获利为w(元).
x(元/kg)
7
8
9
y(kg)
4300
4200
4100
(1)直接写出日销售量y与销售单价x之间的函数关系式为 y=﹣100x+5000 ;(不用写自变量的取值范围)
(2)当销售单价定为多少时,销售这种板栗日获利w最大?最大利润为多少元?
(3)当销售单价在什么范围内时,日获利w不低于42000元?
【分析】(1)用待定系数法求解即可;
(2)由题意可得w关于x的二次函数,将其写成顶点式,然后根据二次函数的性质可得答案;
(3)由题意可得w关于x的一元二次方程,求得方程的根,再结合x的取值范围,可得答案.
解:(1)设y与x之间的函数关系式为y=kx+b(k≠0),
把x=7,y=4300和x=8,y=4200代入得:
,
解得:,
∴日销售量y与销售单价x之间的函数关系式为y=﹣100x+5000;
(2)由题意得:
w=(x﹣6)(﹣100x+5000)
=﹣100x2+5600x﹣30000
=﹣100(x﹣28)2+48400,
∵a=﹣100<0,对称轴为直线x=28.
∴当x=28时,w有最大值为48400元.
∴当销售单价定为28元时,销售这种板栗日获利w最大,最大利润为48400元;
(3)当w=42000元时,有:42000=﹣100(x﹣28)2+48400,
∴x1=20,x2=36,
∵a=﹣100<0,
∴当20≤x≤36时,w≥42000,
又∵6≤x≤30,
∴当20≤x≤30时,日获利w不低于42000元.
八、(本题满分14分)
23.如图,在边长为2的菱形ABCD中,∠C=60°,E是边BC的中点,连接DE,AE.
(1)直接写出DE的长为 3 .
(2)F为边CD上的一点,连接AF,交DE于点G,连接EF,若AF⊥EF.
①求证:△AGE∽△DGF.
②求DF的长.
【分析】(1)由菱形性质可得△BCD为等边三角形,DE⊥BC,再由三角函数可得sinC===,得DE=3;
(2)①先证明△AGD∽△EGF,得,又∠AGE=∠DGF,可证明△AGE∽△DGF;
②如图,过点E作EH⊥CD于点H,在直角三角形ADE中可由勾股定理得AE=,EF==,在直角三角形ECH中可得CH===,EH=,在直角三角形EFH中,由勾股定理可得FH==,从而CF=+=,故DF=CD﹣CF=.
解:(1)连接BD,由于四边形ABCD为菱形,∠C=60°,
∴△BCD为等边三角形,
又E为BC中点,
∴DE⊥BC,∠DEC=90°,
∴sinC===,解得DE=3.
故答案为:3.
(2)①证明:∵AD∥BC,
∴∠ADG=∠DGC=90°,
∴∠ADG=∠GFE=90°,
又∠AGD=∠EGF,
∴△AGD∽△EGF,
∴,
∵∠AGE=∠DGF,
∴△AGE∽△DGF.
②如图,过点E作EH⊥CD于点H,
∵△AGE∽△DGF,
∴∠EAG=∠FDG=30°,
∵∠GFE=∠ADG=90°,
在直角三角形ADE中,由勾股定理可得:
AE===,
∴EF==,
在直角三角形ECH中,∠CEH=30°,
∴CH===,EH=,
在直角三角形EFH中,由勾股定理可得:
FH===,
∴CF=+=,
∴DF=CD﹣CF=.
一、选择题(共10小题,每小题4分,满分40分)
1.计算:tan45°的结果是( )
A.
B.1
C.
D.
2.抛物线y=﹣3x2+2的顶点坐标为( )
A.(0,0)
B.(﹣3,﹣2)
C.(﹣3,2)
D.(0,2)
3.下列反比例函数图象的一个分支在第三象限的是( )
A.
B.
C.
D.
4.在一张缩印出来的纸上,一个三角形的一条边由原图中的6cm变成了2cm,则缩印出的三角形的周长是原图中三角形周长的( )
A.
B.
C.
D.
5.如图,双曲线y1=与直线y2=ax相交于A,B两点,点A的坐标为(2,m),若y1<y2,则x的取值范围是( )
A.x>2或﹣1<x<0
B.﹣2<x<0或0<x<2
C.x>2或﹣2<x<0
D.x<﹣2或0<x<2
6.某同学在利用描点法画二次函数y=ax2+bx+c(a≠0)的图象时,先取自变量x的一些值,计算出相应的函数值y,如下表所示:
x
…
0
1
2
3
4
…
y
…
﹣3
0
﹣1
0
3
…
接着,他在描点时发现,表格中有一组数据计算错误,他计算错误的一组数据是( )
A.
B.
C.
D.
7.如图,△OAB与△OCD是以点O为位似中心的位似图形,相似比为1:2,∠OCD=90°,CO=CD.若B(1,0),则点C的坐标为( )
A.(1,2)
B.(1,1)
C.(,)
D.(2,1)
8.如图,乐器上的一根弦AB=80cm,两个端点A,B固定在乐器板面上,支撑点C是靠近点B的黄金分割点,支撑点D是靠近点A的黄金分割点,则C,D之间的距离为( )
A.(40﹣40)cm
B.(80﹣40)cm
C.(120﹣40)cm
D.(80﹣160)cm
9.如图,在△ABC中,∠BAC=120°,AC=6,AB=4,则BC的长是( )
A.6
B.2
C.2
D.9
10.已知函数y=ax2+bx+c,当y>0时,.则函数y=cx2﹣bx+a的图象可能是下图中的( )
A.
B.
C.
D.
二、填空题(本大题共4小题,每小题5分,满分20分)
11.如果2x=5y(y≠0),那么=
.
12.在Rt△ABC中,∠C=90°,AC=5,BC=12,则sinA=
.
13.已知二次函数y=ax2﹣2x+1的图象与x轴只有一个公共点,则a的值是
.
14.如图,正方形ABCD中,点F在边AB上,且AF:FB=1:2,AC与DF交于点N.
(1)当AB=4时,AN=
.
(2)S△ANF:S四边形CNFB=
.(S表示面积)
三、(本大题共2小题,每小题8分,满分16分)
15.计算:2cos245°+tan60°?tan30°﹣cos60°
16.已知x与y成反比例,且当x=﹣时,y=
(1)求y关于x的函数表达式;
(2)当x=﹣时,y的值是多少?
四、(本大题共2小题,每小题8分,满分16分)
17.如图,a∥b∥c,直线m,n与直线a,b,c分别相交于点A,B,C和点D,E,F.若AB=3,BC=5,DE=4,求EF的长.
18.如图,在边长为1个单位长度的小正方形组成的网格中,△ABC与△A'B'C'以点O为位似中心,且它们的顶点都为网格线的交点.
(1)在图中画出点O(要保留画图痕迹),并直接写出:△ABC与△A'B'C'的位似比是
.
(2)请在此网格中,以点C为位似中心,再画一个△A1B1C,使它与△ABC的位似比等于2:1.
五、(本大题共2小题,每小题10分,满分20分)
19.如图,旗杆AB竖立在斜坡CB的顶端,斜坡CB长为65米,坡度为i=.小明从与点C相距115米的点D处向上爬12米到达建筑物DE的顶端点E.在此测得旗杆顶端点A的仰角为39°,求旗杆的高度AB.(参考数据:sin39°≈0.63,cos39°≈0.78,tan39°≈0.81)
20.如图,在平面直角坐标系中,正比例函数y=kx的图象与反比例函数y=的图象经过点A(2,2).
(1)分别求这两个函数的表达式;
(2)将直线OA向上平移3个单位长度后与y轴交于B,与反比例函数图象在第一象限内的交点为C,连接AB,AC,求点C的坐标及△ABC的面积;
六、(本题满分12分)
21.如图.在△ABC中.AB=4,D是AB上的一点(不与点A,B重合),过点D作DE∥BC,交AC于点E.连接DC,设△ABC的面积为S,△DEC的面积为S′.
(1)当D是AB的中点时,直接写出=
.
(2)若AD=x,=y,求y关于x的函数关系式以及自变量x的取值范围.
七、(本题满分12分)
22.网络直播销售已经成为一种热门的销售方式,某生产商在一销售平台上进行直播销售板栗.已知板栗的成本价为6元/kg,每日销售量y(kg)与销售单价x(元/kg)满足一次函数关系,下表记录的是有关数据,经销售发现,销售单价不低于成本价且不高于30元/kg.设公司销售板栗的日获利为w(元).
x(元/kg)
7
8
9
y(kg)
4300
4200
4100
(1)直接写出日销售量y与销售单价x之间的函数关系式为
;(不用写自变量的取值范围)
(2)当销售单价定为多少时,销售这种板栗日获利w最大?最大利润为多少元?
(3)当销售单价在什么范围内时,日获利w不低于42000元?
八、(本题满分14分)
23.如图,在边长为2的菱形ABCD中,∠C=60°,E是边BC的中点,连接DE,AE.
(1)直接写出DE的长为
.
(2)F为边CD上的一点,连接AF,交DE于点G,连接EF,若AF⊥EF.
①求证:△AGE∽△DGF.
②求DF的长.
参考答案
一、选择题(本大题共10小题,每小题4分,满分40分)
1.计算:tan45°的结果是( )
A.
B.1
C.
D.
【分析】根据我们记忆的特殊角的三角函数值即可得出答案.
解:tan45°=1.
故选:B.
2.抛物线y=﹣3x2+2的顶点坐标为( )
A.(0,0)
B.(﹣3,﹣2)
C.(﹣3,2)
D.(0,2)
【分析】由抛物线顶点式y=a(x﹣h)2+k的顶点坐标为(h,k),直接得到答案.
解:抛物线y=﹣3x2+2的顶点坐标为(0,2),
故选:D.
3.下列反比例函数图象的一个分支在第三象限的是( )
A.
B.
C.
D.
【分析】当k>0,双曲线的两支分别位于第一、第三象限,在每一象限内y随x的增大而减小,依据反比例函数的性质进行判断即可.
解:A.y=图象位于第二、四象限,不合题意;
B.y=图象位于第一、三象限,符合题意;
C.y=图象不一定位于第一、三象限,不合题意;
D.y=图象位于第二、四象限,不合题意;
故选:B.
4.在一张缩印出来的纸上,一个三角形的一条边由原图中的6cm变成了2cm,则缩印出的三角形的周长是原图中三角形周长的( )
A.
B.
C.
D.
【分析】根据相似三角形的周长比等于相似比计算,得到答案.
解:∵三角形的一条边由原图中的6cm变成了2cm,
∴原三角形与缩印出的三角形是相似比为3:1,
∴原三角形与缩印出的三角形的周长比为3:1,
∴缩印出的三角形的周长是原图中三角形周长的,
故选:A.
5.如图,双曲线y1=与直线y2=ax相交于A,B两点,点A的坐标为(2,m),若y1<y2,则x的取值范围是( )
A.x>2或﹣1<x<0
B.﹣2<x<0或0<x<2
C.x>2或﹣2<x<0
D.x<﹣2或0<x<2
【分析】根据反比例函数和正比例函数的对称性求得B(﹣2,﹣m),然后根据函数图象的上下位置关系结合交点的横坐标,即可得出不等式y1<y2的解集.
解:∵双曲线y1=与直线y2=ax相交于A,B两点,点的坐标为(2,m),
∴B(﹣2,﹣m),
又∵y1<y2,
∴x的取值范围是﹣2<x<0或x>2.
故选:C.
6.某同学在利用描点法画二次函数y=ax2+bx+c(a≠0)的图象时,先取自变量x的一些值,计算出相应的函数值y,如下表所示:
x
…
0
1
2
3
4
…
y
…
﹣3
0
﹣1
0
3
…
接着,他在描点时发现,表格中有一组数据计算错误,他计算错误的一组数据是( )
A.
B.
C.
D.
【分析】利用表中数据和二次函数的性质得到抛物线的对称轴为直线x=2,则顶点坐标为(2,﹣1),于是可判断抛物线的开口向上,则x=0和x=4的函数值相等且大于0,然后可判断A选项错误.
解:∵x=1和x=3时,y=0;
∴抛物线的对称轴为直线x=2,
∴顶点坐标为(2,﹣1),
∴抛物线的开口向上,
∴x=0和x=4的函数值相等且大于0,
∴x=0,y=﹣3错误.
故选:A.
7.如图,△OAB与△OCD是以点O为位似中心的位似图形,相似比为1:2,∠OCD=90°,CO=CD.若B(1,0),则点C的坐标为( )
A.(1,2)
B.(1,1)
C.(,)
D.(2,1)
【分析】首先利用等腰直角三角形的性质得出A点坐标,再利用位似是特殊的相似,若两个图形△ABC和△A′B′C′以原点为位似中心,相似比是k,△ABC上一点的坐标是(x,y),则在△A′B′C′中,它的对应点的坐标是(kx,ky)或(﹣kx,ky),进而求出即可.
解:∵∠OAB=∠OCD=90°,AO=AB,CO=CD,等腰Rt△OAB与等腰Rt△OCD是位似图形,点B的坐标为(1,0),
∴BO=1,则AO=AB=,
∴A(,),
∵等腰Rt△OAB与等腰Rt△OCD是位似图形,O为位似中心,相似比为1:2,
∴点C的坐标为:(1,1).
故选:B.
8.如图,乐器上的一根弦AB=80cm,两个端点A,B固定在乐器板面上,支撑点C是靠近点B的黄金分割点,支撑点D是靠近点A的黄金分割点,则C,D之间的距离为( )
A.(40﹣40)cm
B.(80﹣40)cm
C.(120﹣40)cm
D.(80﹣160)cm
【分析】根据黄金分割的概念和黄金比值求出AC=BD=40﹣40,进而得出答案.
解:∵点C是靠近点B的黄金分割点,点D是靠近点A的黄金分割点,
∴AC=BD=80×=40﹣40,
∴CD=BD﹣(AB﹣BD)=2BD﹣AB=80﹣160,
故选:D.
9.如图,在△ABC中,∠BAC=120°,AC=6,AB=4,则BC的长是( )
A.6
B.2
C.2
D.9
【分析】作CD⊥AB,根据直角三角形的性质求出AD,根据勾股定理求出CD,根据勾股定理计算,得到答案.
解:过点C作CD⊥AB,交BA的延长线于点D,
∵∠BAC=120°,
∴∠DAC=180°﹣120°=60°,
∴∠ACD=30°,
∴AD=AC=3,
∴BD=AB+AD=7,
由勾股定理得,CD==3,
在Rt△BCD中,BC==2,
故选:B.
10.已知函数y=ax2+bx+c,当y>0时,.则函数y=cx2﹣bx+a的图象可能是下图中的( )
A.
B.
C.
D.
【分析】当y>0时,,所以可判断a<0,可知﹣=﹣+=﹣,=﹣×=﹣,所以可知a=6b,a=﹣6c,则b=﹣c,不妨设c=1进而得出解析式,找出符合要求的答案.
解:因为函数y=ax2+bx+c,当y>0时,
所以可判断a<0,可知﹣=﹣+=﹣,=﹣×=﹣
所以可知a=6b,a=﹣6c,则b=﹣c,不妨设c=1
则函数y=cx2﹣bx+a为函数y=x2+x﹣6
即y=(x﹣2)(x+3)
则可判断与x轴的交点坐标是(2,0),(﹣3,0),
故选:A.
二、填空题(本大题共4小题,每小题5分,满分20分)
11.如果2x=5y(y≠0),那么= .
【分析】根据比例的性质直接求解即可.
解:∵2x=5y(y≠0),
∴=.
故答案为:.
12.在Rt△ABC中,∠C=90°,AC=5,BC=12,则sinA= .
【分析】根据题意画出图形,进而利用勾股定理得出AB的长,再利用锐角三角函数关系,即可得出答案.
解:如图所示:∵∠C=90°,AC=5,BC=12,
∴AB==13,
∴sinA=.
故答案为:.
13.已知二次函数y=ax2﹣2x+1的图象与x轴只有一个公共点,则a的值是 1 .
【分析】由抛物线y=ax2+bx+c与x轴只有一个公共点,得到b2﹣4ac=0,即可求出a的值.
解:∵二次函数y=ax2﹣2x+1的图象与x轴只有一个公共点,
∴b2﹣4ac=4﹣4a=0,
∴a=1,
故答案为1.
14.如图,正方形ABCD中,点F在边AB上,且AF:FB=1:2,AC与DF交于点N.
(1)当AB=4时,AN= .
(2)S△ANF:S四边形CNFB= 1:11 .(S表示面积)
【分析】(1)根据正方形的性质得到AB∥CD,从而推出△AFN∽△CDN,利用相似三角形的性质得到,结合图形根据线段之间的和差关系推出=,进而根据正方形的性质、线段之间的和差关系和比例关系求解即可;
(2)根据相似三角形的性质推出S△CDN=9S△AFN,根据线段的比例关系推出S△ADN=3S△AFN,从而结合图形推出S四边形CNFB=11S△AFN,进行求解即可.
解:(1)∵四边形ABCD是正方形,
∴AB=CD,AB∥CD,
∴△AFN∽△CDN,
∴,
∵AF:FB=1:2,AF+BF=AB,
∴AF:AB=1:3,
∴=,
∵AB=4,AC是正方形ABCD的对角线,
∴AC=4,
又AN+CN=AC,
∴AN=AC=,
故答案为:;
(2)由(1)得△AFN∽△CDN,且AN:CN=1:3,
∴S△AFN:S△CDN=1:9,
∴S△CDN=9S△AFN,
又FN:DN=1:3,
∴S△AFN:S△ADN=1:3,
∴S△ADN=3S△AFN,
∴S△ABC=S△ADC=S△CDN+S△ADN=12S△AFN,
∴S四边形CNFB=S△ABC﹣S△AFN=11S△AFN,
∴S△ANF:S四边形CNFB=1:11,
故答案为:1:11.
三、(本大题共2小题,每小题8分,满分16分)
15.计算:2cos245°+tan60°?tan30°﹣cos60°
【分析】把特殊角的三角函数值代入计算,得到答案.
解:原式=2×()2+×﹣
=1+1﹣
=.
16.已知x与y成反比例,且当x=﹣时,y=
(1)求y关于x的函数表达式;
(2)当x=﹣时,y的值是多少?
【分析】(1)设xy=k(k为常数,k≠0),把x与y的值代入求出k的值,即可确定出解析式;
(2)把x的值代入解析式求出y的值即可.
解:(1)∵x与y成反比例,
∴可设xy=k(k为常数,k≠0),
∵当x=﹣时,y=,
∴解得k=﹣1,
所以y关于x的表达式y=﹣;
(2)当x=﹣时,y=.
四、(本大题共2小题,每小题8分,满分16分)
17.如图,a∥b∥c,直线m,n与直线a,b,c分别相交于点A,B,C和点D,E,F.若AB=3,BC=5,DE=4,求EF的长.
【分析】根据平行线分线段成比例定理,列出比例式求解即可得到答案.
解:∵a∥b∥c,
∴,
即,
解得:EF=.
18.如图,在边长为1个单位长度的小正方形组成的网格中,△ABC与△A'B'C'以点O为位似中心,且它们的顶点都为网格线的交点.
(1)在图中画出点O(要保留画图痕迹),并直接写出:△ABC与△A'B'C'的位似比是 1:2 .
(2)请在此网格中,以点C为位似中心,再画一个△A1B1C,使它与△ABC的位似比等于2:1.
【分析】(1)直接利用位似图形的性质得出位似中心的位置;
(2)直接利用位似比得出对应点位置进而得出答案.
解:(1)如图所示:点O即为所求,△ABC与△A'B'C'的位似比是:1;2;
故答案为:1:2;
(2)如图所示:△A1B1C即为所求.
五、(本大题共2小题,每小题10分,满分20分)
19.如图,旗杆AB竖立在斜坡CB的顶端,斜坡CB长为65米,坡度为i=.小明从与点C相距115米的点D处向上爬12米到达建筑物DE的顶端点E.在此测得旗杆顶端点A的仰角为39°,求旗杆的高度AB.(参考数据:sin39°≈0.63,cos39°≈0.78,tan39°≈0.81)
【分析】过点B作BF⊥CD,垂足为F,过点E作EG⊥BF,垂足为G,通过作高,构造直角三角形,利用直角三角形的边角关系和坡度即可求出答案.
解:过点B作BF⊥CD,垂足为F,过点E作EG⊥BF,垂足为G,
在Rt△BCF中,
由斜坡BC的坡度i=,
得,=,
∵BC=65米,
设BF=12x(米),FC=5x(米),
由勾股定理得,(12x)2+(5x)2=652,
∴x=5,
∴BF=60米,FC=25米,
∵DC=115米,
∴DF=DC﹣FC=115﹣25=90(米)=EG,
在Rt△AEG中,AG=EG?tan39°≈90×0.81=72.9(米),
∴AB=AG+FG﹣BF=72.9+12﹣60=24.9(米),
答:旗杆的高度AB为24.9米.
20.如图,在平面直角坐标系中,正比例函数y=kx的图象与反比例函数y=的图象经过点A(2,2).
(1)分别求这两个函数的表达式;
(2)将直线OA向上平移3个单位长度后与y轴交于B,与反比例函数图象在第一象限内的交点为C,连接AB,AC,求点C的坐标及△ABC的面积;
【分析】(1)把A点坐标分别代入y=kx和y=中分别求出k、m即可;
(2)利用直线平移的规律得到直线BC的解析式为y=x+3,则B(0,3)再解方程组得点C的坐标为(1,4);连接OC,根据三角形面积公式,利用S△ABC=S△OBC进行计算.
解:(1)把A(2,2)代入y=kx得2k=2,解得k=1;
把A(2,2)代入y=得m=2×2=4,
∴正比例函数的解析式为y=x;反比例函数的解析式为y=;
(2)直线y=x向上平移3的单位得到直线BC的解析式为y=x+3,
当x=0时,y=x+3=3,则B(0,3),
解方程组得或,
∴点C的坐标为(1,4);
连接OC,
S△ABC=S△OBC=×3×1=.
六、(本题满分12分)
21.如图.在△ABC中.AB=4,D是AB上的一点(不与点A,B重合),过点D作DE∥BC,交AC于点E.连接DC,设△ABC的面积为S,△DEC的面积为S′.
(1)当D是AB的中点时,直接写出= .
(2)若AD=x,=y,求y关于x的函数关系式以及自变量x的取值范围.
【分析】(1)先根据DE∥BC推△ADE∽△ABC,再进一步推=,再根据△ADE与△CED等底同高,求S△ADE=S△CED,等量代换最后求出;
(2)求==①,再求=②,①÷②得最后结果.
解:(1)∵DE∥BC,
∴△ADE∽△ABC,
∴=,
∵D是AB的中点,
∴DE是△ABC的中位线,
∴=,AE=EC
∴=,
∵△ADE与△CED等底同高,
∴S△ADE=S△CED,
∵设△ABC的面积为S,△DEC的面积为S′,
∴=.
故答案为:.
(2)∵AB=4,AD=x,DE∥BC,
∴△ADE∽△ABC
∴==①,
=,
∴=,
∵△ADE与△CEDD,AE、EC边同高,
∴=②,
∴①÷②得,
∵设△ABC的面积为S,△DEC的面积为S′,=y,
∴y=﹣x2+x,
∵AB=4,
∴自变量x的取值范围是0<x<4.
七、(本题满分12分)
22.网络直播销售已经成为一种热门的销售方式,某生产商在一销售平台上进行直播销售板栗.已知板栗的成本价为6元/kg,每日销售量y(kg)与销售单价x(元/kg)满足一次函数关系,下表记录的是有关数据,经销售发现,销售单价不低于成本价且不高于30元/kg.设公司销售板栗的日获利为w(元).
x(元/kg)
7
8
9
y(kg)
4300
4200
4100
(1)直接写出日销售量y与销售单价x之间的函数关系式为 y=﹣100x+5000 ;(不用写自变量的取值范围)
(2)当销售单价定为多少时,销售这种板栗日获利w最大?最大利润为多少元?
(3)当销售单价在什么范围内时,日获利w不低于42000元?
【分析】(1)用待定系数法求解即可;
(2)由题意可得w关于x的二次函数,将其写成顶点式,然后根据二次函数的性质可得答案;
(3)由题意可得w关于x的一元二次方程,求得方程的根,再结合x的取值范围,可得答案.
解:(1)设y与x之间的函数关系式为y=kx+b(k≠0),
把x=7,y=4300和x=8,y=4200代入得:
,
解得:,
∴日销售量y与销售单价x之间的函数关系式为y=﹣100x+5000;
(2)由题意得:
w=(x﹣6)(﹣100x+5000)
=﹣100x2+5600x﹣30000
=﹣100(x﹣28)2+48400,
∵a=﹣100<0,对称轴为直线x=28.
∴当x=28时,w有最大值为48400元.
∴当销售单价定为28元时,销售这种板栗日获利w最大,最大利润为48400元;
(3)当w=42000元时,有:42000=﹣100(x﹣28)2+48400,
∴x1=20,x2=36,
∵a=﹣100<0,
∴当20≤x≤36时,w≥42000,
又∵6≤x≤30,
∴当20≤x≤30时,日获利w不低于42000元.
八、(本题满分14分)
23.如图,在边长为2的菱形ABCD中,∠C=60°,E是边BC的中点,连接DE,AE.
(1)直接写出DE的长为 3 .
(2)F为边CD上的一点,连接AF,交DE于点G,连接EF,若AF⊥EF.
①求证:△AGE∽△DGF.
②求DF的长.
【分析】(1)由菱形性质可得△BCD为等边三角形,DE⊥BC,再由三角函数可得sinC===,得DE=3;
(2)①先证明△AGD∽△EGF,得,又∠AGE=∠DGF,可证明△AGE∽△DGF;
②如图,过点E作EH⊥CD于点H,在直角三角形ADE中可由勾股定理得AE=,EF==,在直角三角形ECH中可得CH===,EH=,在直角三角形EFH中,由勾股定理可得FH==,从而CF=+=,故DF=CD﹣CF=.
解:(1)连接BD,由于四边形ABCD为菱形,∠C=60°,
∴△BCD为等边三角形,
又E为BC中点,
∴DE⊥BC,∠DEC=90°,
∴sinC===,解得DE=3.
故答案为:3.
(2)①证明:∵AD∥BC,
∴∠ADG=∠DGC=90°,
∴∠ADG=∠GFE=90°,
又∠AGD=∠EGF,
∴△AGD∽△EGF,
∴,
∵∠AGE=∠DGF,
∴△AGE∽△DGF.
②如图,过点E作EH⊥CD于点H,
∵△AGE∽△DGF,
∴∠EAG=∠FDG=30°,
∵∠GFE=∠ADG=90°,
在直角三角形ADE中,由勾股定理可得:
AE===,
∴EF==,
在直角三角形ECH中,∠CEH=30°,
∴CH===,EH=,
在直角三角形EFH中,由勾股定理可得:
FH===,
∴CF=+=,
∴DF=CD﹣CF=.
同课章节目录
