正余弦定理的应用(新课标A版)
图片预览











文档简介
(共38张PPT)
数学网络自习室
主讲:朱成
2011.1
正弦定理及其变形
正弦定理及其变形
边角分离
正弦定理及其变形
边角分离
正弦定理及其变形
边角分离
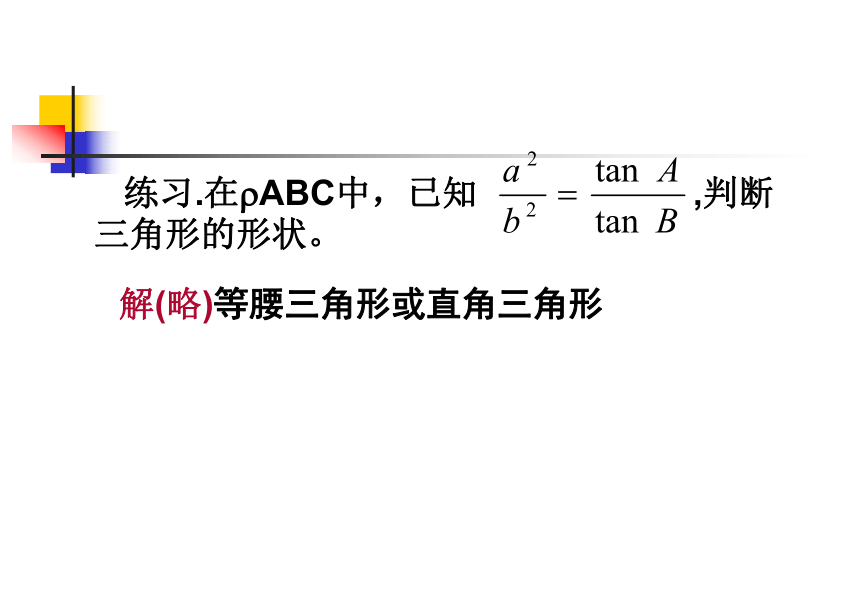
练习.在 ABC中,已知 ,判断三角形的形状。
练习.在 ABC中,已知 ,判断三角形的形状。
练习.在 ABC中,已知 ,判断三角形的形状。
解(略)等腰三角形或直角三角形
练习
2,在△ABC 中,已知
(a+b+c)(b+c-a)=3bc,且sin2A=sinBsinC,
判断三角形的形状。
一、要点复习:余弦定理
一、要点复习:余弦定理
一、要点复习:余弦定理
一、要点复习:余弦定理
变形
一、要点复习:余弦定理
变形
二、余弦定理应用
(1)已知三边
(2)已知两边和夹角
二、余弦定理应用
(1)已知三边
(2)已知两边和夹角
练习题答案: 1. 7; 2. 90°; 3. 7.
在三角形中,已知(a+b)(a- b)=c(b+c),求角A.
问题2:
在三角形中,已知(a+b)(a- b)=c(b+c),求角A.
问题2:
解:条件整理变形得
C
A
B
a
c
b
A=120
0
动手实践:在 ABC中,已知
,求角B.
变式3:
在 ABC中,已知
求角C.
开拓创新:
1.在 ABC中,证明:
2.求
的值.
例4 在△ABC中,a、b、c分别是A、B、C的对边,试证明:a=bcosC+ccosB
例4 在△ABC中,a、b、c分别是A、B、C的对边,试证明:a=bcosC+ccosB
证明:由余弦定理知: ,
右边=
A
B
C
D
c
b
a
三,已知三角形形状,
讨论边的取值范围。
2 当△ABC直角三角形时(c>a>b)
当△ABC为钝角三角形时(c>b>a)
当△ABC为锐角三角形时(c>b>a)
当△ABC为锐角三角形时
例1,a ,a+1,a+2 构成钝角三角形,求a 的取值范围。
例2,锐角三角形的三边长为2,x,3,
求x的取值范围。
练习:
三条线段长度为2,x,6
(1)求构成直角三角形时,x的取值范围
(2)求构成锐角三角形时,x的取值范围
(3)求构成钝角三角形时,x的取值范围
例题精选
例3 已知△ABC的三内角A、B、C成等差,而A、B、C三内角的对边a、b、c成等比.试证明:△ABC为正三角形.
例题精选
例3 已知△ABC的三内角A、B、C成等差,而A、B、C三内角的对边a、b、c成等比.试证明:△ABC为正三角形.
证明:
∵a、b、c成等比,∴b2=ac
∵A、B、C成等差,∴2B=A+C,
又A+B+C=180o,∴B=60o,A+C=120o
又由余弦定理得:
∴
,即
,∴a=c
又∵B=60o,∴△ABC是正三角形.
例题精选
例4 在△ABC中,如果 ,
并且B为锐角,试判断此三角形的形状特征。
例题精选
例4 在△ABC中,如果 ,
并且B为锐角,试判断此三角形的形状特征。
解:由 ,
得:
B=45o
,将A=135o-C代入上式,得
∴C=90o
,综上所述,△ABC是等腰直角三角形。
例题精选
例5 在△ABC中,已知, 且
则∠B等于多少?
例题精选
例5 在△ABC中,已知, 且
则∠B等于多少?
答案: ∠B=30o
本课小测
1、在△ABC中,一定成立的等式是( )
(A)asinA=bsinA (B)asinB=bsinA
(C)acosA=bcosB (D)acosB=bcosA
2、在△ABC中,A>B是sinA>sinB的( )
(A)充分不必要条件 (B)必要不充分条件
(C)充要条件 (D)既不充分也不必要条件
3、在△ABC中,若A:B:C=3:4:5,则a:b:c等于( )
(A) (B)
(C) (D)
本课小测
4、 在△ABC中,A=60o,b=1,S△ABC=
?
5、已知△ABC中,满足acosA=bcosB,试判断△ABC的形状。
练习1 在△ABC中,已知
1)A=120o,B=30o,a=8,求c;
2)a=14,b=7 ,B= ,求A;
3)b= ,c= ,A=120o,求a;
4)a=2,b=3,c= ,求C
经验:根据已知条件适当选用正弦定理、余弦定理。
数学网络自习室
主讲:朱成
2011.1
正弦定理及其变形
正弦定理及其变形
边角分离
正弦定理及其变形
边角分离
正弦定理及其变形
边角分离
练习.在 ABC中,已知 ,判断三角形的形状。
练习.在 ABC中,已知 ,判断三角形的形状。
练习.在 ABC中,已知 ,判断三角形的形状。
解(略)等腰三角形或直角三角形
练习
2,在△ABC 中,已知
(a+b+c)(b+c-a)=3bc,且sin2A=sinBsinC,
判断三角形的形状。
一、要点复习:余弦定理
一、要点复习:余弦定理
一、要点复习:余弦定理
一、要点复习:余弦定理
变形
一、要点复习:余弦定理
变形
二、余弦定理应用
(1)已知三边
(2)已知两边和夹角
二、余弦定理应用
(1)已知三边
(2)已知两边和夹角
练习题答案: 1. 7; 2. 90°; 3. 7.
在三角形中,已知(a+b)(a- b)=c(b+c),求角A.
问题2:
在三角形中,已知(a+b)(a- b)=c(b+c),求角A.
问题2:
解:条件整理变形得
C
A
B
a
c
b
A=120
0
动手实践:在 ABC中,已知
,求角B.
变式3:
在 ABC中,已知
求角C.
开拓创新:
1.在 ABC中,证明:
2.求
的值.
例4 在△ABC中,a、b、c分别是A、B、C的对边,试证明:a=bcosC+ccosB
例4 在△ABC中,a、b、c分别是A、B、C的对边,试证明:a=bcosC+ccosB
证明:由余弦定理知: ,
右边=
A
B
C
D
c
b
a
三,已知三角形形状,
讨论边的取值范围。
2 当△ABC直角三角形时(c>a>b)
当△ABC为钝角三角形时(c>b>a)
当△ABC为锐角三角形时(c>b>a)
当△ABC为锐角三角形时
例1,a ,a+1,a+2 构成钝角三角形,求a 的取值范围。
例2,锐角三角形的三边长为2,x,3,
求x的取值范围。
练习:
三条线段长度为2,x,6
(1)求构成直角三角形时,x的取值范围
(2)求构成锐角三角形时,x的取值范围
(3)求构成钝角三角形时,x的取值范围
例题精选
例3 已知△ABC的三内角A、B、C成等差,而A、B、C三内角的对边a、b、c成等比.试证明:△ABC为正三角形.
例题精选
例3 已知△ABC的三内角A、B、C成等差,而A、B、C三内角的对边a、b、c成等比.试证明:△ABC为正三角形.
证明:
∵a、b、c成等比,∴b2=ac
∵A、B、C成等差,∴2B=A+C,
又A+B+C=180o,∴B=60o,A+C=120o
又由余弦定理得:
∴
,即
,∴a=c
又∵B=60o,∴△ABC是正三角形.
例题精选
例4 在△ABC中,如果 ,
并且B为锐角,试判断此三角形的形状特征。
例题精选
例4 在△ABC中,如果 ,
并且B为锐角,试判断此三角形的形状特征。
解:由 ,
得:
B=45o
,将A=135o-C代入上式,得
∴C=90o
,综上所述,△ABC是等腰直角三角形。
例题精选
例5 在△ABC中,已知, 且
则∠B等于多少?
例题精选
例5 在△ABC中,已知, 且
则∠B等于多少?
答案: ∠B=30o
本课小测
1、在△ABC中,一定成立的等式是( )
(A)asinA=bsinA (B)asinB=bsinA
(C)acosA=bcosB (D)acosB=bcosA
2、在△ABC中,A>B是sinA>sinB的( )
(A)充分不必要条件 (B)必要不充分条件
(C)充要条件 (D)既不充分也不必要条件
3、在△ABC中,若A:B:C=3:4:5,则a:b:c等于( )
(A) (B)
(C) (D)
本课小测
4、 在△ABC中,A=60o,b=1,S△ABC=
?
5、已知△ABC中,满足acosA=bcosB,试判断△ABC的形状。
练习1 在△ABC中,已知
1)A=120o,B=30o,a=8,求c;
2)a=14,b=7 ,B= ,求A;
3)b= ,c= ,A=120o,求a;
4)a=2,b=3,c= ,求C
经验:根据已知条件适当选用正弦定理、余弦定理。
