3.2.2直线的两点式方程(1)
文档属性
| 名称 | 3.2.2直线的两点式方程(1) |  | |
| 格式 | zip | ||
| 文件大小 | 396.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-07-08 19:26:58 | ||
图片预览








文档简介
(共25张PPT)
复习
直线方程名称 已知
条件 直线方程 使用范围
点
斜
式
斜
截
式
斜率k和直线在y轴上的截距
点
和斜率k
斜率必须存在
斜率不存在时,
解:设直线方程为:y=kx+b.
由已知得:
得:
所以,直线方程为: y=x+2
有其他做法吗?介绍新的知识与方法
所以,直线方程为: y=x+2
将A(1,3),k=1代入点斜式,
得: y-3=x-1
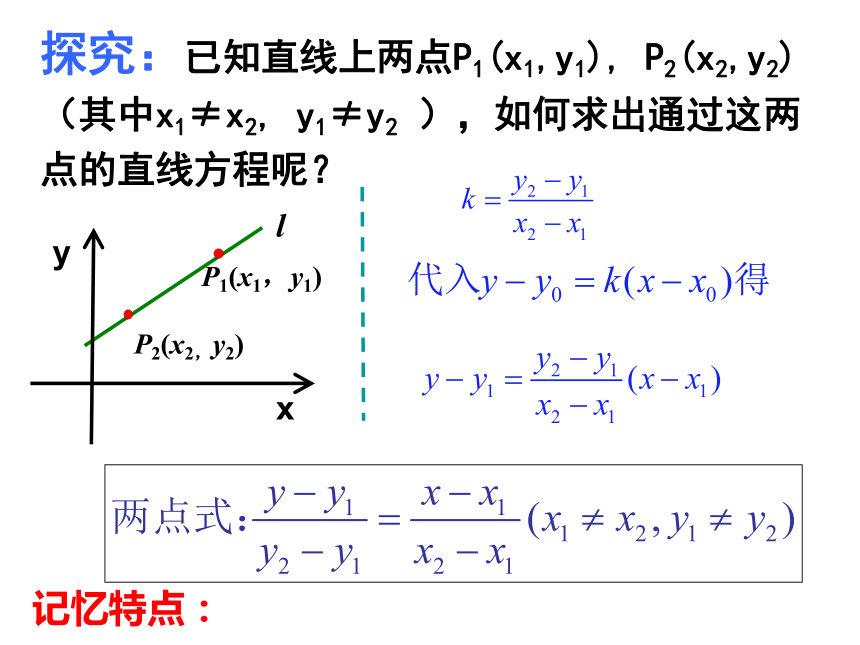
3.2.2 直线的两点式方程
x
y
l
P2(x2,y2)
P1(x1,y1)
探究:已知直线上两点P1(x1,y1), P2(x2,y2)(其中x1≠x2, y1≠y2 ),如何求出通过这两点的直线方程呢?
记忆特点:
记忆特点:
左边全为y,右边全为x
两边的分母全为常数
分子,分母中的减数相同
说明:
(1)这个方程是由直线上两点确定;叫两点式.
(2)当直线没斜率或斜率为0时,不能用两点式来表示;
1.求经过下列两点的直线的两点式方程,再化斜截式方程.
(1)P(2,1),Q(0,-3)
(2)A(0,5),B(5,0)
(3)C(-4,-5),D(0,0)
课堂练习:
方法小结
已知两点坐标,求直线方程的方法:
①用两点式
②先求出斜率k,再用点斜式。
截距式方程
x
y
l
A(a,0)
截距式方程
B(0,b)
代入两点式方程得
化简得
横截距
纵截距
截距式适用于横、纵截距都存在且都不为0的直线.
2.根据下列条件求直线方程
(1)在x轴上的截距为2,在y轴上的截距是3;
(2)在x轴上的截距为-5,在y轴上的截距是6;
由截距式得: 整理得:
由截距式得: 整理得:
练习
中点坐标公式
x
y
A(x1,y1)
B(x2,y2)
中点
例2、三角形的顶点是A(-5,0),B(3,-3),C(0,2),
求BC边所在直线的方程,以及该边上中线所在直线的方程.
x
y
O
C
B
A
.
.
.
.
M
变式1:BC边上垂直平分线所在直线的方程
变式2:BC边上高所在直线的方程
3x-5y+15=0
3x-5y-7=0
小结
点斜式
斜率和一点坐标
斜截式
斜率k和截距b
两点坐标
两点式
点斜式
两个截距
截距式
y-y1=k(x-x1)
(1)这个方程是由直线上一点和斜率确定的
(2)当直线l的倾斜角为0°时,直线方程为y=y1
(3)当直线倾斜角90°时,直线没有斜率,方程
式不能用点斜式表示,直线方程为x=x1
▲
▲
▲
▲
1.点斜式:
y=kx+b
说明:
(1)上述方程是由直线l的斜率和它的纵截距确定的,叫做直线的方程的斜截式。
(2)纵截距可以大于0,也可以等于0或小于0。
2.斜截式:
说明:
(1)这个方程是由直线上两点确定;
(2)当直线没斜率或斜率为0时,不能用两点式来表示;
3.两点式:
说明:
(1)这一直线方程是由直线的纵截距和横截距所确定;
(2)截距式适用于纵,横截距都存在且都不为0的直线;
4.截距式:
对截距概念的深刻理解
求过定点P(1,2)且横截距比纵截距大1的直线方程
求过(1,2)并且在两个坐标轴上的截距相等的直线
解:
那还有一条呢?
y=2x (与x轴和y轴的截距都为0)
所以直线方程为:x+y-3=0
即:a=3
把(1,2)代入得:
设 直线的方程为:
对截距概念的深刻理解
当两截距都等于0时
当两截距都不为0时
法二:用点斜式求解
解:三条
变: 过(1,2)并且在两个坐标轴上的截距的
绝对值相等的直线有几条
解得:a=b=3或a=-b=-1
直线方程为:y+x-3=0、y-x-1=0或y=2x
设
对截距概念的深刻理解
变:过(1,2)并且在y轴上的截距是x轴上的截距的2倍的直线是( )
A、 x+y-3=0 B、x+y-3=0或y=2x
C、 2x+y-4=0 D、2x+y-4=0或y=2x
对截距概念的深刻理解
已知直线l过定点P(3,2)且与x轴、y轴的正半轴分别交
于A、B两点。求△AOB面积的最小值及此时l的方程
练习:
数形结合与对称的灵活应用
已知一条光线从点A(2,-1)发出、经x轴反射后,
通过点B(-2,-4),试求点P坐标
A(2,-1)
(x,0)
B(-2,-4)
P
变:已知两点A(2,-1)、B(-2,-4)
试在x轴上求一点P,使|PA|+|PB|最小
变:试在x轴上求一点P,使|PB|-|PA|最大
数形结合与对称的灵活应用
已知直线l:x-2y+8=0和两点A(2,0)、B(-2,-4)
(1)求点A关于直线l的对称点
(2)在直线l是求一点P,使|PA|+|PB|最小
(3)在直线l是求一点Q,使|PA|-|PB|最大
A(2,0)
A1(x,y)
G
B(-2,-4)
P
A(2,0)
G
B(-2,-4)
(-2,8)
(-2,3)
(12,10)
小结
点斜式
斜率和一点坐标
斜截式
斜率k和截距b
两点坐标
两点式
点斜式
两个截距
截距式
复习
直线方程名称 已知
条件 直线方程 使用范围
点
斜
式
斜
截
式
斜率k和直线在y轴上的截距
点
和斜率k
斜率必须存在
斜率不存在时,
解:设直线方程为:y=kx+b.
由已知得:
得:
所以,直线方程为: y=x+2
有其他做法吗?介绍新的知识与方法
所以,直线方程为: y=x+2
将A(1,3),k=1代入点斜式,
得: y-3=x-1
3.2.2 直线的两点式方程
x
y
l
P2(x2,y2)
P1(x1,y1)
探究:已知直线上两点P1(x1,y1), P2(x2,y2)(其中x1≠x2, y1≠y2 ),如何求出通过这两点的直线方程呢?
记忆特点:
记忆特点:
左边全为y,右边全为x
两边的分母全为常数
分子,分母中的减数相同
说明:
(1)这个方程是由直线上两点确定;叫两点式.
(2)当直线没斜率或斜率为0时,不能用两点式来表示;
1.求经过下列两点的直线的两点式方程,再化斜截式方程.
(1)P(2,1),Q(0,-3)
(2)A(0,5),B(5,0)
(3)C(-4,-5),D(0,0)
课堂练习:
方法小结
已知两点坐标,求直线方程的方法:
①用两点式
②先求出斜率k,再用点斜式。
截距式方程
x
y
l
A(a,0)
截距式方程
B(0,b)
代入两点式方程得
化简得
横截距
纵截距
截距式适用于横、纵截距都存在且都不为0的直线.
2.根据下列条件求直线方程
(1)在x轴上的截距为2,在y轴上的截距是3;
(2)在x轴上的截距为-5,在y轴上的截距是6;
由截距式得: 整理得:
由截距式得: 整理得:
练习
中点坐标公式
x
y
A(x1,y1)
B(x2,y2)
中点
例2、三角形的顶点是A(-5,0),B(3,-3),C(0,2),
求BC边所在直线的方程,以及该边上中线所在直线的方程.
x
y
O
C
B
A
.
.
.
.
M
变式1:BC边上垂直平分线所在直线的方程
变式2:BC边上高所在直线的方程
3x-5y+15=0
3x-5y-7=0
小结
点斜式
斜率和一点坐标
斜截式
斜率k和截距b
两点坐标
两点式
点斜式
两个截距
截距式
y-y1=k(x-x1)
(1)这个方程是由直线上一点和斜率确定的
(2)当直线l的倾斜角为0°时,直线方程为y=y1
(3)当直线倾斜角90°时,直线没有斜率,方程
式不能用点斜式表示,直线方程为x=x1
▲
▲
▲
▲
1.点斜式:
y=kx+b
说明:
(1)上述方程是由直线l的斜率和它的纵截距确定的,叫做直线的方程的斜截式。
(2)纵截距可以大于0,也可以等于0或小于0。
2.斜截式:
说明:
(1)这个方程是由直线上两点确定;
(2)当直线没斜率或斜率为0时,不能用两点式来表示;
3.两点式:
说明:
(1)这一直线方程是由直线的纵截距和横截距所确定;
(2)截距式适用于纵,横截距都存在且都不为0的直线;
4.截距式:
对截距概念的深刻理解
求过定点P(1,2)且横截距比纵截距大1的直线方程
求过(1,2)并且在两个坐标轴上的截距相等的直线
解:
那还有一条呢?
y=2x (与x轴和y轴的截距都为0)
所以直线方程为:x+y-3=0
即:a=3
把(1,2)代入得:
设 直线的方程为:
对截距概念的深刻理解
当两截距都等于0时
当两截距都不为0时
法二:用点斜式求解
解:三条
变: 过(1,2)并且在两个坐标轴上的截距的
绝对值相等的直线有几条
解得:a=b=3或a=-b=-1
直线方程为:y+x-3=0、y-x-1=0或y=2x
设
对截距概念的深刻理解
变:过(1,2)并且在y轴上的截距是x轴上的截距的2倍的直线是( )
A、 x+y-3=0 B、x+y-3=0或y=2x
C、 2x+y-4=0 D、2x+y-4=0或y=2x
对截距概念的深刻理解
已知直线l过定点P(3,2)且与x轴、y轴的正半轴分别交
于A、B两点。求△AOB面积的最小值及此时l的方程
练习:
数形结合与对称的灵活应用
已知一条光线从点A(2,-1)发出、经x轴反射后,
通过点B(-2,-4),试求点P坐标
A(2,-1)
(x,0)
B(-2,-4)
P
变:已知两点A(2,-1)、B(-2,-4)
试在x轴上求一点P,使|PA|+|PB|最小
变:试在x轴上求一点P,使|PB|-|PA|最大
数形结合与对称的灵活应用
已知直线l:x-2y+8=0和两点A(2,0)、B(-2,-4)
(1)求点A关于直线l的对称点
(2)在直线l是求一点P,使|PA|+|PB|最小
(3)在直线l是求一点Q,使|PA|-|PB|最大
A(2,0)
A1(x,y)
G
B(-2,-4)
P
A(2,0)
G
B(-2,-4)
(-2,8)
(-2,3)
(12,10)
小结
点斜式
斜率和一点坐标
斜截式
斜率k和截距b
两点坐标
两点式
点斜式
两个截距
截距式
