人教版七年级上册第一章1.5.1《有理数的乘方》课件(共19张PPT)
文档属性
| 名称 | 人教版七年级上册第一章1.5.1《有理数的乘方》课件(共19张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-19 00:00:00 | ||
图片预览






文档简介
(共19张PPT)
七年级上册人民教育出版社
1.5.1有理数的乘方
一、情景导入
珠穆朗玛峰是世界的最高峰,它的海拔高度是8844米。把一张足够大的厚度为0.1毫米的纸,连续对折30次的厚度能超过珠穆朗玛峰,这是真的吗?
二、探索新知
探究点一:乘方的概念
如图,一正方形的边长为5cm,则它的面积为_____平方厘米;
一正方体的棱长为5cm,
则它的体积为______
立方厘米.
5×5
5×5×5
二、探索新知
探究点一:乘方的概念
相同因数的乘法如何简化?
5×5记作:
5×5×5
记作:
5×5×5×5×5×5记作:
52
53
56
读作:5的平方或5的2次方
读作:5的立方或5的3次方
读作:5的6次方
如果是任意多个相同的有理数相乘,我们如何去简化表示呢?
二、探索新知
探究点一:乘方的概念
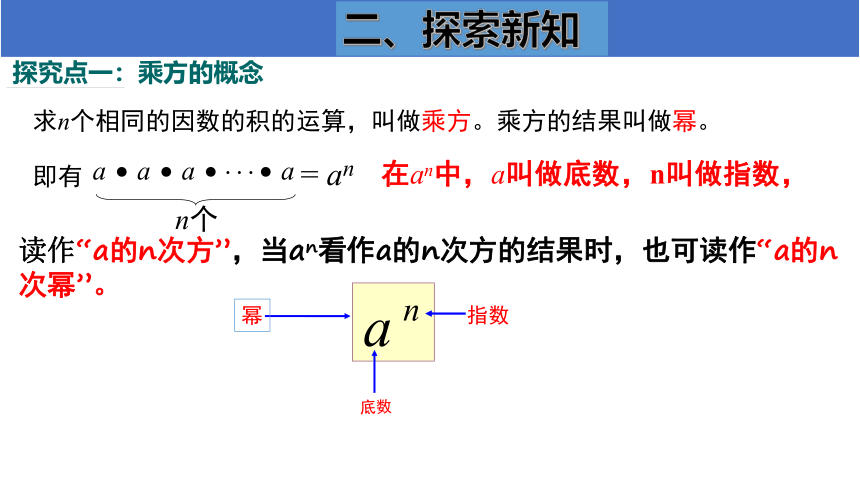
求n个相同的因数的积的运算,叫做乘方。乘方的结果叫做幂。即有
=
an
n个
在an中,a叫做底数,n叫做指数,
读作“a的n次方”,当an看作a的n次方的结果时,也可读作“a的n次幂”。
幂
指数
底数
二、探索新知
把下列乘法式子写成乘方的形式
1、1×1×1×1×1×1×1=
2、8=
3、3×3×3×3×3=
4、(-5)×(-5)×(-5)×(-5)=
5、
二、探索新知
(1)1的任何次方都等于1。
(2)一个数可以看作这个数本身的一次方,1常常省略不写。
(3)底数一定是相同的因数,当底数是分数或者是负数时,要用括号括起来。
合作交流:
二、探索新知
_____________________________
_______________________________
指点迷津:
二、探索新知
101=
102=
103=
104=
......
(
-10)1=
(
-10)2=
(
-10)3=
(
-10)4=
......
01=
____
02=____
03=
04=
......
探究点2:乘方运算的符号法则
计算并观察:你发现怎样的符号规律?
归纳:幂的符号法则
(1)正数的任何次幂是正数
(2)负数的奇次幂是
负数,负数的偶次幂是正数
(3)0的任何正整数次幂都是0
(4)互为相反数的两个数的奇次幂互为相反数,偶次幂相等
(
5)任何一个数的偶次幂都是非负数
10
100
1000
10000
-10
100
-1000
10000
0
0
0
0
三、典例分析
闯关大赛:
第一关
_________,
________,
________________,
________________,
____________,
底数
指数
____________,
_________,
__________,
三、典例分析
闯关大赛:
第一关
三、典例分析
乘方运算先定号,再定值
第二关
三、典例分析
例
3
指出下列各式的底数和指数,并计算其结果
第三关
第四关
(1)-(-3)2=
;
(2)-32=
;
(3)(-5)3=
;
(4)0.13=
;
(5)(-1)9=
;
(6)(-1)12=
;
(7)(-1)2n=
;
(8)(-1)2n+1=
;
-9
-9
-125
0.001
-1
1
1
-1
(9)(-1)n=
.
(当n为奇数时)
(当n为偶数时).
四、课堂练习
1、填空
五、能力提升
第
五
关
2、判断题:
(√)
(√)
(√)
(√)
(×)
(×)
(×)
五、能力提升
当n为奇数时,
__________________
__________________
当n为正整数时,
当n为奇数时,
__________________
0
1
第六关
这节课你学到了什么?谈谈你的收获吧!
1.求几个相同因数的积的运算,叫做乘方.
2.乘方的符号法则:
(1)正数的任何次幂都是正数
(2)负数的奇次幂是负数,负数的偶次幂是正数
(3)零的任何正整数次幂都是零
(4)互为相反数的两个数的奇次幂互为相反数,偶次幂相等
(5)任何一个数的偶次幂都是非负数
3.注意:
二者的区别及相互关系;
幂
指数
底数
六、课堂小结
作业布置:
作业1:习题1.5第一题
作业2:计算1~20的平方;1~10的三次方。
七年级上册人民教育出版社
1.5.1有理数的乘方
一、情景导入
珠穆朗玛峰是世界的最高峰,它的海拔高度是8844米。把一张足够大的厚度为0.1毫米的纸,连续对折30次的厚度能超过珠穆朗玛峰,这是真的吗?
二、探索新知
探究点一:乘方的概念
如图,一正方形的边长为5cm,则它的面积为_____平方厘米;
一正方体的棱长为5cm,
则它的体积为______
立方厘米.
5×5
5×5×5
二、探索新知
探究点一:乘方的概念
相同因数的乘法如何简化?
5×5记作:
5×5×5
记作:
5×5×5×5×5×5记作:
52
53
56
读作:5的平方或5的2次方
读作:5的立方或5的3次方
读作:5的6次方
如果是任意多个相同的有理数相乘,我们如何去简化表示呢?
二、探索新知
探究点一:乘方的概念
求n个相同的因数的积的运算,叫做乘方。乘方的结果叫做幂。即有
=
an
n个
在an中,a叫做底数,n叫做指数,
读作“a的n次方”,当an看作a的n次方的结果时,也可读作“a的n次幂”。
幂
指数
底数
二、探索新知
把下列乘法式子写成乘方的形式
1、1×1×1×1×1×1×1=
2、8=
3、3×3×3×3×3=
4、(-5)×(-5)×(-5)×(-5)=
5、
二、探索新知
(1)1的任何次方都等于1。
(2)一个数可以看作这个数本身的一次方,1常常省略不写。
(3)底数一定是相同的因数,当底数是分数或者是负数时,要用括号括起来。
合作交流:
二、探索新知
_____________________________
_______________________________
指点迷津:
二、探索新知
101=
102=
103=
104=
......
(
-10)1=
(
-10)2=
(
-10)3=
(
-10)4=
......
01=
____
02=____
03=
04=
......
探究点2:乘方运算的符号法则
计算并观察:你发现怎样的符号规律?
归纳:幂的符号法则
(1)正数的任何次幂是正数
(2)负数的奇次幂是
负数,负数的偶次幂是正数
(3)0的任何正整数次幂都是0
(4)互为相反数的两个数的奇次幂互为相反数,偶次幂相等
(
5)任何一个数的偶次幂都是非负数
10
100
1000
10000
-10
100
-1000
10000
0
0
0
0
三、典例分析
闯关大赛:
第一关
_________,
________,
________________,
________________,
____________,
底数
指数
____________,
_________,
__________,
三、典例分析
闯关大赛:
第一关
三、典例分析
乘方运算先定号,再定值
第二关
三、典例分析
例
3
指出下列各式的底数和指数,并计算其结果
第三关
第四关
(1)-(-3)2=
;
(2)-32=
;
(3)(-5)3=
;
(4)0.13=
;
(5)(-1)9=
;
(6)(-1)12=
;
(7)(-1)2n=
;
(8)(-1)2n+1=
;
-9
-9
-125
0.001
-1
1
1
-1
(9)(-1)n=
.
(当n为奇数时)
(当n为偶数时).
四、课堂练习
1、填空
五、能力提升
第
五
关
2、判断题:
(√)
(√)
(√)
(√)
(×)
(×)
(×)
五、能力提升
当n为奇数时,
__________________
__________________
当n为正整数时,
当n为奇数时,
__________________
0
1
第六关
这节课你学到了什么?谈谈你的收获吧!
1.求几个相同因数的积的运算,叫做乘方.
2.乘方的符号法则:
(1)正数的任何次幂都是正数
(2)负数的奇次幂是负数,负数的偶次幂是正数
(3)零的任何正整数次幂都是零
(4)互为相反数的两个数的奇次幂互为相反数,偶次幂相等
(5)任何一个数的偶次幂都是非负数
3.注意:
二者的区别及相互关系;
幂
指数
底数
六、课堂小结
作业布置:
作业1:习题1.5第一题
作业2:计算1~20的平方;1~10的三次方。
