江苏省如东县掘港高级中学2011-2012学年高一第二学期第四次学情调研考试数学试题
文档属性
| 名称 | 江苏省如东县掘港高级中学2011-2012学年高一第二学期第四次学情调研考试数学试题 |  | |
| 格式 | zip | ||
| 文件大小 | 105.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-07-09 08:59:16 | ||
图片预览



文档简介
如东县掘港高级中学高一第二学期数学第四次调研考试
一、填空题:本大题共14小题,每小题5分,共计70分.
1.函数的最小正周期为 .
2.已知向量,,若,则实数的值为 .
3.已知过点和的直线与直线平行,则的值为 .
4.已知,,则 .
5. .
6.已知,,,则向量的夹角为 .
7.圆心在直线上的圆与轴交于两点,则圆的方程为 .
8.从原点向圆作两条切线,则这两条切线的夹角的大小为 .
9.将函数的图象向右平移个单位,得到图象的函数解析式为,则的值等于 .
10.若圆上有且仅有两个点到直线4x+3y=11的距离等于1,则半径R的取值范围是 .
11.若,, 则 .
12.在△ABC中,sinA=,cosB=,则cosC等于 .
13.下面有五个命题:
①函数y=sin4x-cos4x的最小正周期是.②终边在y轴上的角的集合是{a|a=|.
③在同一坐标系中,函数y=sinx的图象和函数y=x的图象有三个公共点.
④把函数
⑤函数
其中真命题的序号是 ((写出所有真命题的编号)).
14.设集合,,
若 则实数m的取值范围是
二、解答题:本大题共6小题,共计90分.
15.已知,,且.(1)求的值;
(2)若,,且,求的值.
16、已知圆C与圆x2+y2-2x =0相外切,并且与直线相切于点,
求圆C的方程.
18.在△ABC中,角A、B、C的对边分别是a、b、c,已知c=2,C=.
(1)若△ABC的面积等于,求a,b的值;(2)若sinC+sin(B-A)=2sin2A,求角A的大小.
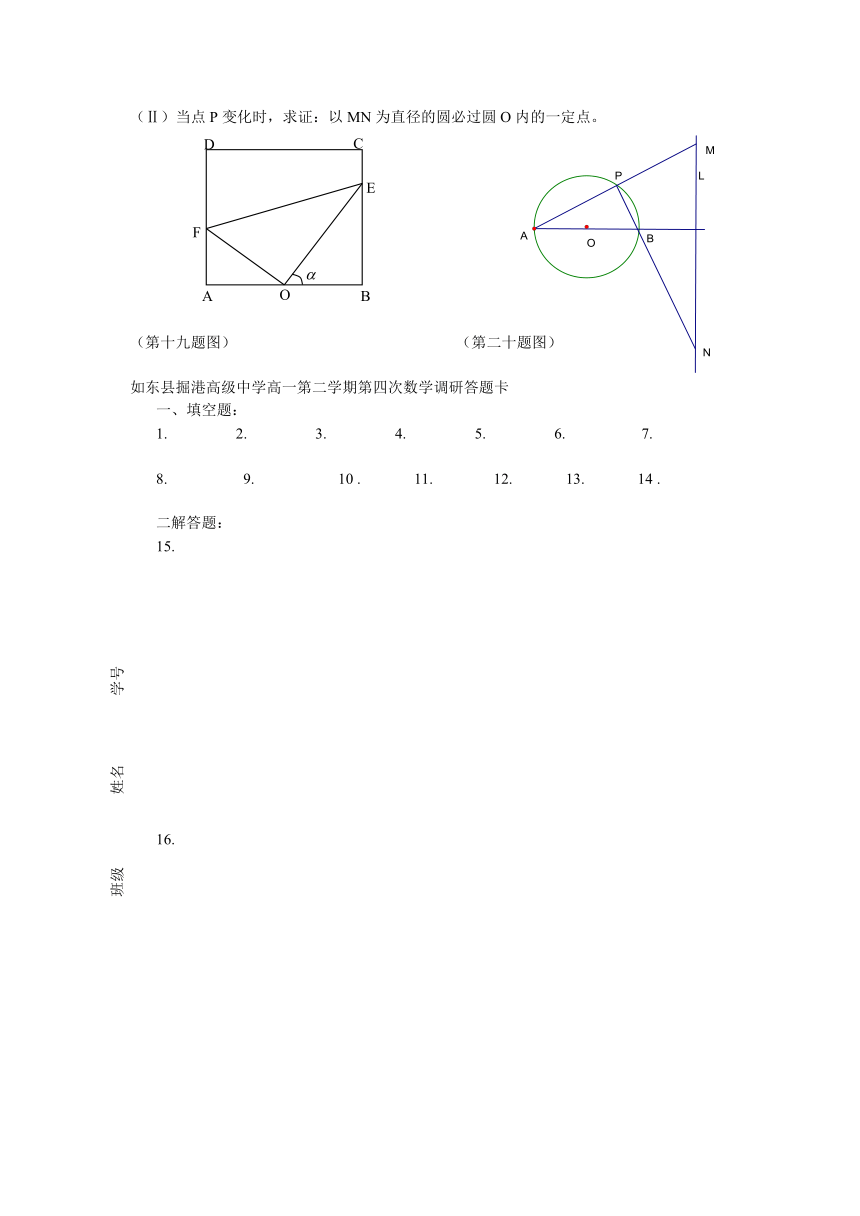
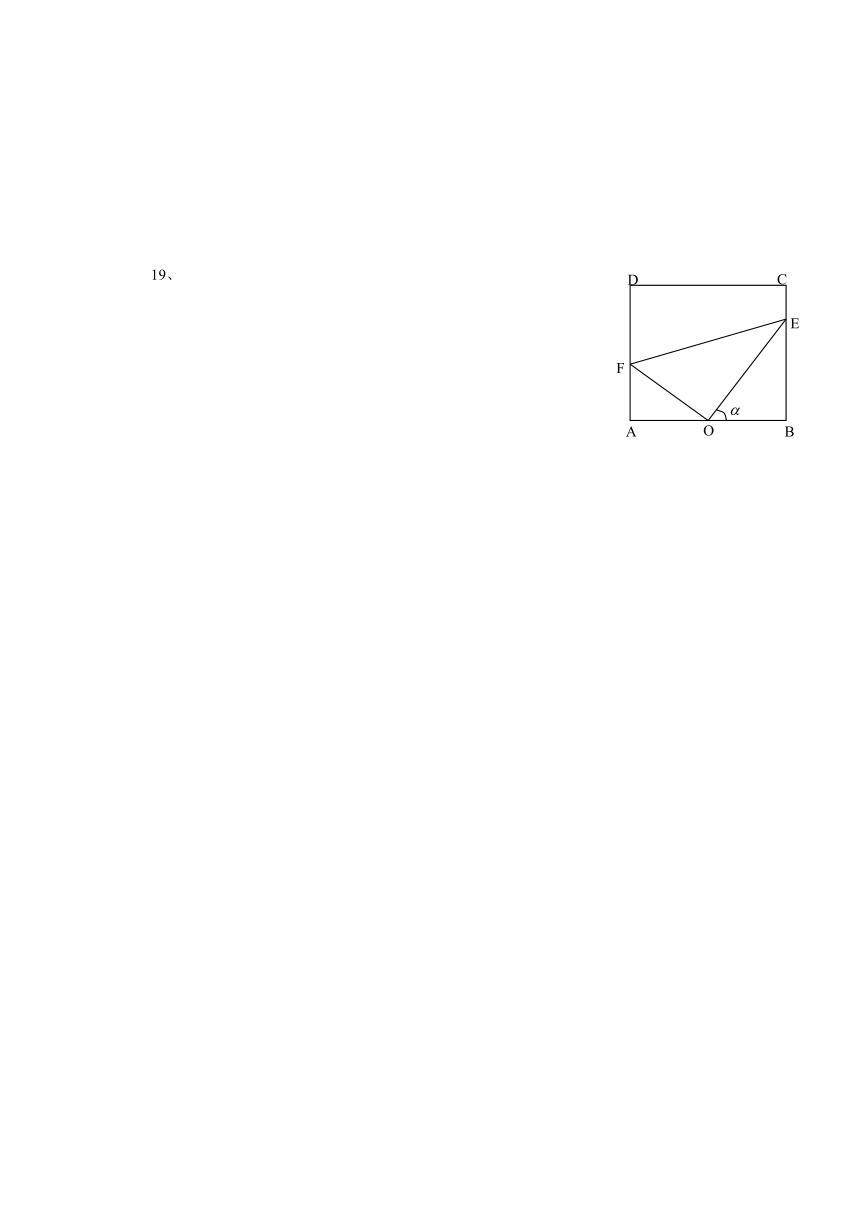
19.某居民小区内建有一块矩形草坪ABCD,AB=50米,BC=米,为了便于居民平时休闲散步,
该小区物业管理公司将在这块草坪内铺设三条小路OE、EF和OF,考虑到小区整体规划,
要求O是AB的中点,点E在边BC上,点F在边AD上,且∠EOF=90°,如图所示.
(1)设∠BOE=,试将的周长表示成的函数关系式,并求出此函数的定义域;
(2)经核算,三条路每米铺设费用均为400元,试问如何设计才能使铺路的总费用最低?
并求出最低总费用.
20.如图,已知圆O的直径AB=4,定直线L到圆心的距离为4,且直线L垂直直线AB。点P是圆O上异于A、B的任意一点,直线PA、PB分别交L与M、N点。
(Ⅰ)若∠PAB=30°,求以MN为直径的圆方程;
(Ⅱ)当点P变化时,求证:以MN为直径的圆必过圆O内的一定点。
(第十九题图) (第二十题图)
如东县掘港高级中学高一第二学期第四次数学调研答题卡
一、填空题:1. 2. 3. 4. 5. 6. 7. 8. 9. 10 . 11. 12. 13. 14 .
二解答题:15.
16.
17.
18.19、20
如东县掘港高级中学高一第二学期数学第四次调研考试
参考答案与评分标准
一.填空题:
1. 2. 3. 4.5 5.5x —12y—36=0;5x+12y+36=0 6. 7.;8. ; 9. ;10.112.,13.① ④,14
二.解答题:
15.解:解:(1)∵,∴,即,从而.…………4分
∴=……………7分
(2) 由及,得.………………………9分
又,∴,
∴, ……………………………………………10分
………………12分
∵,∴..……………………………………………………………14分
16..设圆C的圆心为(a,b ),则,…………7分
则有a=4,b=0,r=2或a=0,b=,r=6,
∴圆C的方程为(x-4)2+y2=4或.…………14分
17.解:(1).…………4分
(2)…………9分
(3)…………14分
18.解:(1)由余弦定理及条件,得a2+b2-ab=4,absinC=,即ab=4.
联立方程组解得a=2,b=2.…………8分
(2)由题意,得eq \f(,2)+sin(-2A)=2sin2A.即sin(2A-)=.
因为A∈(0,),所以2A-∈(-,).所以2A-=或2A-=.
则A=,或A=.…………16分
19.解:(1)∵在Rt△BOE中,OB=25, ∠B=90°,∠BOE=,∴OE=.…………2分
在Rt△AOF中,OA=25, ∠A=90°,∠AFO=,∴OF=.……………………4分
又∠EOF=90°,∴EF==,
∴
即. …………………………………………6分
当点F在点D时,这时角最小,求得此时=;
当点E在C点时,这时角最大,求得此时=.
故此函数的定义域为.……………………………………………………………8分
(2)由题意知,要求铺路总费用最低,只要求的周长的最小值即可.
由(1)得,,
设,则,
∴……………………………………………12分
由,,得,∴,
从而,……………………………………………………………15分
当,即BE=25时,,
所以当BE=AE=25米时,铺路总费用最低,最低总费用为元.…………16分
20.解:解:建立如图所示的直角坐标系,
⊙O的方程为,直线L的方程为。…………2分
(Ⅰ)∵∠PAB=30°,∴点P的坐标为,
∴,。
将x=4代入,得。∴MN的中点坐标为(4,0),MN=。
∴以MN为直径的圆的方程为。
同理,当点P在x轴下方时,所求圆的方程仍是。…………8分
(Ⅱ)设点P的坐标为,∴(),∴。
∵,
将x=4代入,得,
。∴,MN=。
MN的中点坐标为。
以MN为直径的圆截x轴的线段长度为
为定值。
∴⊙必过⊙O 内定点。…………16分
D
A
B
C
O
E
F
班级 姓名 学号
D
A
B
C
O
E
F
一、填空题:本大题共14小题,每小题5分,共计70分.
1.函数的最小正周期为 .
2.已知向量,,若,则实数的值为 .
3.已知过点和的直线与直线平行,则的值为 .
4.已知,,则 .
5. .
6.已知,,,则向量的夹角为 .
7.圆心在直线上的圆与轴交于两点,则圆的方程为 .
8.从原点向圆作两条切线,则这两条切线的夹角的大小为 .
9.将函数的图象向右平移个单位,得到图象的函数解析式为,则的值等于 .
10.若圆上有且仅有两个点到直线4x+3y=11的距离等于1,则半径R的取值范围是 .
11.若,, 则 .
12.在△ABC中,sinA=,cosB=,则cosC等于 .
13.下面有五个命题:
①函数y=sin4x-cos4x的最小正周期是.②终边在y轴上的角的集合是{a|a=|.
③在同一坐标系中,函数y=sinx的图象和函数y=x的图象有三个公共点.
④把函数
⑤函数
其中真命题的序号是 ((写出所有真命题的编号)).
14.设集合,,
若 则实数m的取值范围是
二、解答题:本大题共6小题,共计90分.
15.已知,,且.(1)求的值;
(2)若,,且,求的值.
16、已知圆C与圆x2+y2-2x =0相外切,并且与直线相切于点,
求圆C的方程.
18.在△ABC中,角A、B、C的对边分别是a、b、c,已知c=2,C=.
(1)若△ABC的面积等于,求a,b的值;(2)若sinC+sin(B-A)=2sin2A,求角A的大小.
19.某居民小区内建有一块矩形草坪ABCD,AB=50米,BC=米,为了便于居民平时休闲散步,
该小区物业管理公司将在这块草坪内铺设三条小路OE、EF和OF,考虑到小区整体规划,
要求O是AB的中点,点E在边BC上,点F在边AD上,且∠EOF=90°,如图所示.
(1)设∠BOE=,试将的周长表示成的函数关系式,并求出此函数的定义域;
(2)经核算,三条路每米铺设费用均为400元,试问如何设计才能使铺路的总费用最低?
并求出最低总费用.
20.如图,已知圆O的直径AB=4,定直线L到圆心的距离为4,且直线L垂直直线AB。点P是圆O上异于A、B的任意一点,直线PA、PB分别交L与M、N点。
(Ⅰ)若∠PAB=30°,求以MN为直径的圆方程;
(Ⅱ)当点P变化时,求证:以MN为直径的圆必过圆O内的一定点。
(第十九题图) (第二十题图)
如东县掘港高级中学高一第二学期第四次数学调研答题卡
一、填空题:1. 2. 3. 4. 5. 6. 7. 8. 9. 10 . 11. 12. 13. 14 .
二解答题:15.
16.
17.
18.19、20
如东县掘港高级中学高一第二学期数学第四次调研考试
参考答案与评分标准
一.填空题:
1. 2. 3. 4.5 5.5x —12y—36=0;5x+12y+36=0 6. 7.;8. ; 9. ;10.1
二.解答题:
15.解:解:(1)∵,∴,即,从而.…………4分
∴=……………7分
(2) 由及,得.………………………9分
又,∴,
∴, ……………………………………………10分
………………12分
∵,∴..……………………………………………………………14分
16..设圆C的圆心为(a,b ),则,…………7分
则有a=4,b=0,r=2或a=0,b=,r=6,
∴圆C的方程为(x-4)2+y2=4或.…………14分
17.解:(1).…………4分
(2)…………9分
(3)…………14分
18.解:(1)由余弦定理及条件,得a2+b2-ab=4,absinC=,即ab=4.
联立方程组解得a=2,b=2.…………8分
(2)由题意,得eq \f(,2)+sin(-2A)=2sin2A.即sin(2A-)=.
因为A∈(0,),所以2A-∈(-,).所以2A-=或2A-=.
则A=,或A=.…………16分
19.解:(1)∵在Rt△BOE中,OB=25, ∠B=90°,∠BOE=,∴OE=.…………2分
在Rt△AOF中,OA=25, ∠A=90°,∠AFO=,∴OF=.……………………4分
又∠EOF=90°,∴EF==,
∴
即. …………………………………………6分
当点F在点D时,这时角最小,求得此时=;
当点E在C点时,这时角最大,求得此时=.
故此函数的定义域为.……………………………………………………………8分
(2)由题意知,要求铺路总费用最低,只要求的周长的最小值即可.
由(1)得,,
设,则,
∴……………………………………………12分
由,,得,∴,
从而,……………………………………………………………15分
当,即BE=25时,,
所以当BE=AE=25米时,铺路总费用最低,最低总费用为元.…………16分
20.解:解:建立如图所示的直角坐标系,
⊙O的方程为,直线L的方程为。…………2分
(Ⅰ)∵∠PAB=30°,∴点P的坐标为,
∴,。
将x=4代入,得。∴MN的中点坐标为(4,0),MN=。
∴以MN为直径的圆的方程为。
同理,当点P在x轴下方时,所求圆的方程仍是。…………8分
(Ⅱ)设点P的坐标为,∴(),∴。
∵,
将x=4代入,得,
。∴,MN=。
MN的中点坐标为。
以MN为直径的圆截x轴的线段长度为
为定值。
∴⊙必过⊙O 内定点。…………16分
D
A
B
C
O
E
F
班级 姓名 学号
D
A
B
C
O
E
F
同课章节目录
