福建省宁德市部分达标中学2011-2012学年高二第二学期期末联合考试数学(文)试卷
文档属性
| 名称 | 福建省宁德市部分达标中学2011-2012学年高二第二学期期末联合考试数学(文)试卷 |

|
|
| 格式 | zip | ||
| 文件大小 | 205.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-07-09 00:00:00 | ||
图片预览



文档简介
宁德市部分达标中学2011~2012学年第二学期期末联合考试
高二数学试卷(文科)
试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分. 满分150分. 考试时间120分钟。
温馨提示:
1.答题前,考生先将自己的姓名、班级、座号填写在答题卡上.
2.考生作答时,将答案写在答题卡上. 请按照题号在各题的答题区域内作答. 在草稿纸、试题卷上答题无效.
3.考生不能使用计算器答题.
第I卷(选择题 共60分)
一.选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1. 设复数(是虚数单位),则复数在复平面上对应点的坐标为( )
A. (4, 4) B.(2, 4) C.(-2,4) D.(4,-2)
2. 设集合,函数的定义域为集合,则=( )
A. B. C. D.
3.若等比数列{}的各项都是正数,且=16, 则的值为 ( )
A.1 B.2 C. 4 D.8
4. 在△ABC中,角A、B、C所对的边分别为a、b、c.若,B=60°,则边的值为 ( )
A.2 B. 4 C.6 D. 8
5.若抛物线上一点的横坐标坐标为8 ,则点到抛物线焦点的距离为( )
A.8 B.9 C.10 D.12
6. 已知,,向量,则“”是“∥”的( )
A. 充要条件 B. 必要不充分条件
C. 充分不必要条件 D. 既不充分也不必要条件
7.设变量x,y满足约束条件,则目标函数的最大值为( )
A. B.2 C. D.6
8.已知函数,,则函数的图象大致为( )
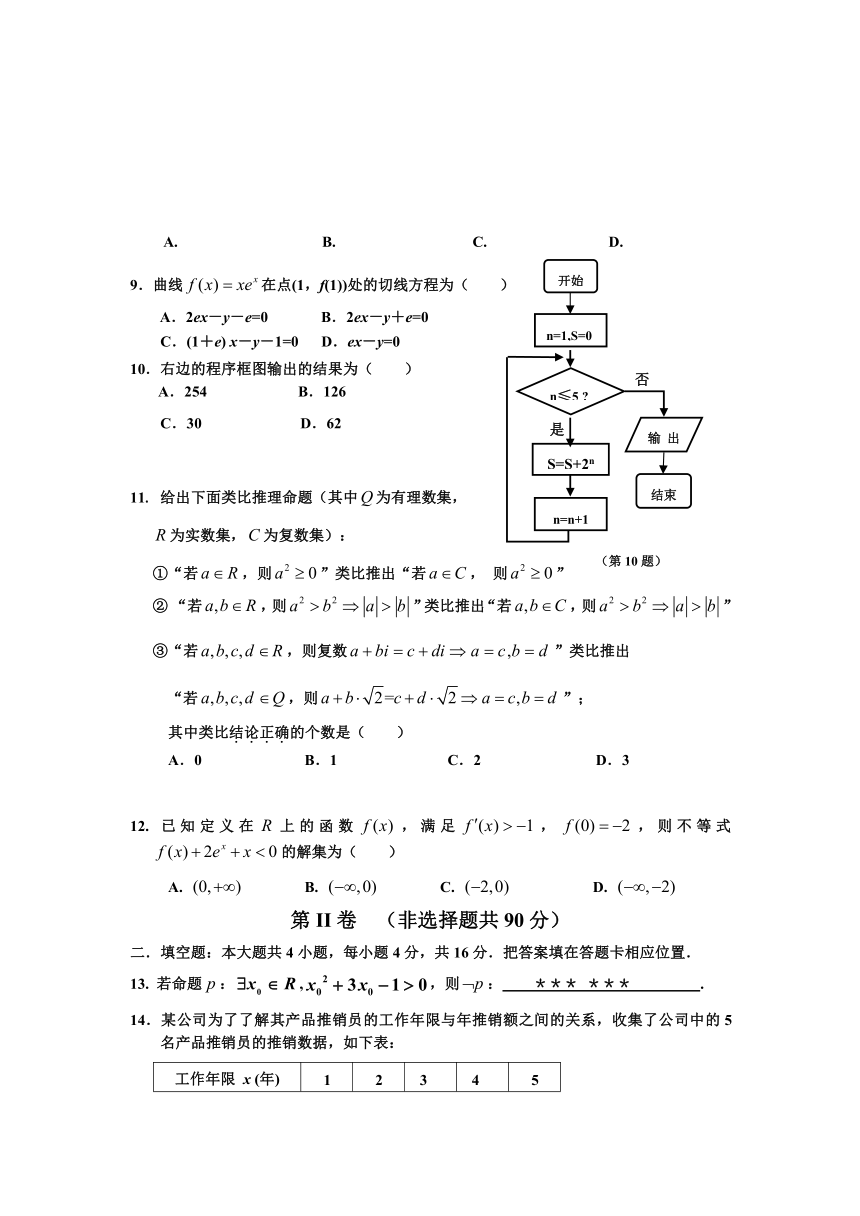
9.曲线在点(1,f(1))处的切线方程为( )
A.2ex-y-e=0 B.2ex-y+e=0
C.(1+e) x-y-1=0 D.ex-y=0
10.右边的程序框图输出的结果为( )
A.254 B.126
C.30 D.62
11. 给出下面类比推理命题(其中为有理数集,
为实数集,为复数集):
①“若,则”类比推出“若, 则”
② “若,则”类比推出“若,则”
③“若,则复数”类比推出
“若,则”;
其中类比结论正确的个数是( )
A.0 B.1 C.2 D.3
12. 已知定义在上的函数,满足,,则不等式的解集为( )
A. B. C. D.
第II卷 (非选择题共90分)
二.填空题:本大题共4小题,每小题4分,共16分.把答案填在答题卡相应位置.
13. 若命题:,,则: *** *** .
14.某公司为了了解其产品推销员的工作年限与年推销额之间的关系,收集了公司中的5名产品推销员的推销数据,如下表:
工作年限 x (年) 1 2 3 4 5
年推销金额y(万元) 0.5 1 2 3 3.5
从散点图分析,x与y具有线性相关且回归方程为,则a的值为 **
15.设函数是周期为4的奇函数,当-2≤x≤0时,,则的值为 *** .
16. 已知分别是双曲线的左、右焦点,过点作斜率为2的直线交双曲线L的左支上方于点P,若为直角,则此双曲线的离心率等于 *** .
三.解答题:本大题共6小题,满分74分.解答须写出文字说明、证明过程和演算步骤.
17. (本小题满分12分)
已知命题:“关于x的方程有两个不相等的实根”;命题:“函数在上单调递减”.
(Ⅰ)求命题与命题分别为真命题时相应的实数的取值范围;
(Ⅱ)若命题“”为真命题。 求实数的取值范围.
18.(本小题满分12分)
已知△ABC中,内角A、B、C的对边分别为、b、c,满足:
且.
(Ⅰ)求角B的大小和△ABC的面积; (Ⅱ)若 求的值.
19.(本小题满分12分)
已知点、都在函数(为常数)的图象上,,数列满足:.
(I)求数列的通项公式; (II)求数列的前项和.
20.(本小题满分12分)
如图所示,某学校的教学楼前有一块矩形空地
,其长为32米,宽为18米,现要在此
空地上种植一块矩形草坪,三边留有人行道,
人行道宽度为米与米(与均不小于2米),
且要求“转角处”(图中矩形)的面积
为8平方米。
(Ⅰ)试用表示草坪的面积,并指出
的取值范围;
(Ⅱ)如何设计人行道的宽度、,才能使
草坪的面积最大?并求出草坪的最大面积。
21. (本小题共12分)
已知椭圆的中心在原点,焦点在x轴上,一个顶点为B(0,-2),离心率为.
(Ⅰ)求椭圆的方程;
(Ⅱ)设过点A(0,3) 的直线l与椭圆交于M、N两点,且|BM|=|BN|,求直线l的方程。
22. (本小题满分14分)
已知函数,,.
(Ⅰ)当时,求与g(x)的公共单调区间;
(Ⅱ)若函数有极值,求实数的何值范围;
(Ⅲ)当<0时,讨论函数h(x) 的零点个数.
宁德市部分达标中学2011-2012学年第二学期期末联合考试
高二数学试卷(文科)参考答案及评分标准
一、选择题:每小题5分,共60分.
题号 1 2 3 4 5 6 7 8 9 10 11 12
答案 B D C A C C D C A D B B
二、填空题:每小题4分,共16分.
13. 14. -2.35 15. 1 16.
三. 解答题:本大题共6小题,满分74分.
17. 解:(Ⅰ)∵方程有两个不相等的实根∴△=.. 1分
解得:m>1或m< -1 ........................................... 3分
∴命题 p为真时,实数的取值范围为: …………… 4分
又∵函数在上单调递减,
且函数的图象是开口向上的抛物线,其对称轴方程是:
,得.
∴命题为真时,实数的取值范围为: ……………………… 8分
(Ⅱ)由(Ⅰ)知
又因为命题“”为真命题,所以真且真
解得: . ..........................……...11分
∴为真命题时,实数的取值范围为 ..........12分
18. 解:(Ⅰ)
∴ 由余弦定理得 . .......................................3分
. ....................................................................... 4分
, , ...........6分
. ...................................................................8分
(Ⅱ)
..................................................11分
......................................................................................................12分
..........................................................6分
20. 解: (Ⅰ)由条件知, ……………………………………… 1分
∵ ∴ ∴ ……………………………………………………………… 3分
∴
即: ……………………………………………………………… 6分
(Ⅱ)∵ ……………………………………………………………… 9分
当,即时,上式取“=”号, 则
即时,取得最大值,最大值为400.…………………………………………………11分
答:当人行道的宽度、分别为米和3米时,草坪的面积达到最大,最大面积是400平方米 ………………………………………12分
21. 解:(Ⅰ)∵椭圆的中心在原点,焦点在x轴上,可设椭圆:
椭圆一个顶点为B(0,-2), , ……………………………1分
∵ 离心率为 ........,,,,,. ①
又....................② ......…………2分 联立① .② 解得, =12 ……………………………………………4分
∴椭圆的方程为:……………………………………………… 5分
(Ⅱ)当直线l斜率不存在时,易知不满足题设要求。可设直线l的方程为:
, 的中点为 ……..…………6分
由 消去x 得 , ……………… 7分
要使直线l与椭圆交于M、N两点,则必须满足:
即 ………………(*)
则,
则 , ……………………………………………8分 ∵|BM|=|BN| ,又 B(0,-2)
, …………………………………………9分
解得: , 满足(*)式 …………………………………………11分
…………………………………12分
22. 解:(Ⅰ)当 ...................... 1分
由得x<-2或x>0, 由得-2<x<0,
∴的单调递增区间是,递减区间是,.... ... ....3分
又g(x)的对称轴为x= -2且开口向上,
∴g(x)的单调递增区间是,递减区间是, ...............4分
∴时, 与g(x)的公共单调递增区间是,无公共递减区间....5分
(Ⅱ)
∴ ..........................6分
(1)当时, 在递增,
在递减, 则有极小值,符合题设. .......... ..................7分
(2)当时, 令=0得,,,
若函数有极值,两个相异实根,∴ ,得
综上(1)(2)得,若函数有极值,实数的何值范围是:
...................................................9分
(Ⅲ)∵a<0, 由得或,
则
将x,,的变化情况列表如下:
x (-∞, -2) -2 (-2, ) (, +∞)
- 0 + 0 -
h ( x ) ↘ 极小值 ↗ 极大值 ↘
∴, ………11分
(另解:设=t, , 亦可)
当即时,在x充分大时,h(x)<0,∴h(x)零点个数为1;
当即a=-3时,h(x)零点个数为2;
当即a<-3时,h(x)零点个数为3; …………13分
综上所述,当-3当a<-3时,h(x)零点个数为3. …………14分
x
y
o
y
x
o
x
y
o
o
y
x
是
否
输出S
结束
n=1,S=0
n≤5
开始
S=S+2n
n=n+1
(第10题)
A. B. C. D.
32
a
a
b
18
高二数学试卷(文科)
试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分. 满分150分. 考试时间120分钟。
温馨提示:
1.答题前,考生先将自己的姓名、班级、座号填写在答题卡上.
2.考生作答时,将答案写在答题卡上. 请按照题号在各题的答题区域内作答. 在草稿纸、试题卷上答题无效.
3.考生不能使用计算器答题.
第I卷(选择题 共60分)
一.选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1. 设复数(是虚数单位),则复数在复平面上对应点的坐标为( )
A. (4, 4) B.(2, 4) C.(-2,4) D.(4,-2)
2. 设集合,函数的定义域为集合,则=( )
A. B. C. D.
3.若等比数列{}的各项都是正数,且=16, 则的值为 ( )
A.1 B.2 C. 4 D.8
4. 在△ABC中,角A、B、C所对的边分别为a、b、c.若,B=60°,则边的值为 ( )
A.2 B. 4 C.6 D. 8
5.若抛物线上一点的横坐标坐标为8 ,则点到抛物线焦点的距离为( )
A.8 B.9 C.10 D.12
6. 已知,,向量,则“”是“∥”的( )
A. 充要条件 B. 必要不充分条件
C. 充分不必要条件 D. 既不充分也不必要条件
7.设变量x,y满足约束条件,则目标函数的最大值为( )
A. B.2 C. D.6
8.已知函数,,则函数的图象大致为( )
9.曲线在点(1,f(1))处的切线方程为( )
A.2ex-y-e=0 B.2ex-y+e=0
C.(1+e) x-y-1=0 D.ex-y=0
10.右边的程序框图输出的结果为( )
A.254 B.126
C.30 D.62
11. 给出下面类比推理命题(其中为有理数集,
为实数集,为复数集):
①“若,则”类比推出“若, 则”
② “若,则”类比推出“若,则”
③“若,则复数”类比推出
“若,则”;
其中类比结论正确的个数是( )
A.0 B.1 C.2 D.3
12. 已知定义在上的函数,满足,,则不等式的解集为( )
A. B. C. D.
第II卷 (非选择题共90分)
二.填空题:本大题共4小题,每小题4分,共16分.把答案填在答题卡相应位置.
13. 若命题:,,则: *** *** .
14.某公司为了了解其产品推销员的工作年限与年推销额之间的关系,收集了公司中的5名产品推销员的推销数据,如下表:
工作年限 x (年) 1 2 3 4 5
年推销金额y(万元) 0.5 1 2 3 3.5
从散点图分析,x与y具有线性相关且回归方程为,则a的值为 **
15.设函数是周期为4的奇函数,当-2≤x≤0时,,则的值为 *** .
16. 已知分别是双曲线的左、右焦点,过点作斜率为2的直线交双曲线L的左支上方于点P,若为直角,则此双曲线的离心率等于 *** .
三.解答题:本大题共6小题,满分74分.解答须写出文字说明、证明过程和演算步骤.
17. (本小题满分12分)
已知命题:“关于x的方程有两个不相等的实根”;命题:“函数在上单调递减”.
(Ⅰ)求命题与命题分别为真命题时相应的实数的取值范围;
(Ⅱ)若命题“”为真命题。 求实数的取值范围.
18.(本小题满分12分)
已知△ABC中,内角A、B、C的对边分别为、b、c,满足:
且.
(Ⅰ)求角B的大小和△ABC的面积; (Ⅱ)若 求的值.
19.(本小题满分12分)
已知点、都在函数(为常数)的图象上,,数列满足:.
(I)求数列的通项公式; (II)求数列的前项和.
20.(本小题满分12分)
如图所示,某学校的教学楼前有一块矩形空地
,其长为32米,宽为18米,现要在此
空地上种植一块矩形草坪,三边留有人行道,
人行道宽度为米与米(与均不小于2米),
且要求“转角处”(图中矩形)的面积
为8平方米。
(Ⅰ)试用表示草坪的面积,并指出
的取值范围;
(Ⅱ)如何设计人行道的宽度、,才能使
草坪的面积最大?并求出草坪的最大面积。
21. (本小题共12分)
已知椭圆的中心在原点,焦点在x轴上,一个顶点为B(0,-2),离心率为.
(Ⅰ)求椭圆的方程;
(Ⅱ)设过点A(0,3) 的直线l与椭圆交于M、N两点,且|BM|=|BN|,求直线l的方程。
22. (本小题满分14分)
已知函数,,.
(Ⅰ)当时,求与g(x)的公共单调区间;
(Ⅱ)若函数有极值,求实数的何值范围;
(Ⅲ)当<0时,讨论函数h(x) 的零点个数.
宁德市部分达标中学2011-2012学年第二学期期末联合考试
高二数学试卷(文科)参考答案及评分标准
一、选择题:每小题5分,共60分.
题号 1 2 3 4 5 6 7 8 9 10 11 12
答案 B D C A C C D C A D B B
二、填空题:每小题4分,共16分.
13. 14. -2.35 15. 1 16.
三. 解答题:本大题共6小题,满分74分.
17. 解:(Ⅰ)∵方程有两个不相等的实根∴△=.. 1分
解得:m>1或m< -1 ........................................... 3分
∴命题 p为真时,实数的取值范围为: …………… 4分
又∵函数在上单调递减,
且函数的图象是开口向上的抛物线,其对称轴方程是:
,得.
∴命题为真时,实数的取值范围为: ……………………… 8分
(Ⅱ)由(Ⅰ)知
又因为命题“”为真命题,所以真且真
解得: . ..........................……...11分
∴为真命题时,实数的取值范围为 ..........12分
18. 解:(Ⅰ)
∴ 由余弦定理得 . .......................................3分
. ....................................................................... 4分
, , ...........6分
. ...................................................................8分
(Ⅱ)
..................................................11分
......................................................................................................12分
..........................................................6分
20. 解: (Ⅰ)由条件知, ……………………………………… 1分
∵ ∴ ∴ ……………………………………………………………… 3分
∴
即: ……………………………………………………………… 6分
(Ⅱ)∵ ……………………………………………………………… 9分
当,即时,上式取“=”号, 则
即时,取得最大值,最大值为400.…………………………………………………11分
答:当人行道的宽度、分别为米和3米时,草坪的面积达到最大,最大面积是400平方米 ………………………………………12分
21. 解:(Ⅰ)∵椭圆的中心在原点,焦点在x轴上,可设椭圆:
椭圆一个顶点为B(0,-2), , ……………………………1分
∵ 离心率为 ........,,,,,. ①
又....................② ......…………2分 联立① .② 解得, =12 ……………………………………………4分
∴椭圆的方程为:……………………………………………… 5分
(Ⅱ)当直线l斜率不存在时,易知不满足题设要求。可设直线l的方程为:
, 的中点为 ……..…………6分
由 消去x 得 , ……………… 7分
要使直线l与椭圆交于M、N两点,则必须满足:
即 ………………(*)
则,
则 , ……………………………………………8分 ∵|BM|=|BN| ,又 B(0,-2)
, …………………………………………9分
解得: , 满足(*)式 …………………………………………11分
…………………………………12分
22. 解:(Ⅰ)当 ...................... 1分
由得x<-2或x>0, 由得-2<x<0,
∴的单调递增区间是,递减区间是,.... ... ....3分
又g(x)的对称轴为x= -2且开口向上,
∴g(x)的单调递增区间是,递减区间是, ...............4分
∴时, 与g(x)的公共单调递增区间是,无公共递减区间....5分
(Ⅱ)
∴ ..........................6分
(1)当时, 在递增,
在递减, 则有极小值,符合题设. .......... ..................7分
(2)当时, 令=0得,,,
若函数有极值,两个相异实根,∴ ,得
综上(1)(2)得,若函数有极值,实数的何值范围是:
...................................................9分
(Ⅲ)∵a<0, 由得或,
则
将x,,的变化情况列表如下:
x (-∞, -2) -2 (-2, ) (, +∞)
- 0 + 0 -
h ( x ) ↘ 极小值 ↗ 极大值 ↘
∴, ………11分
(另解:设=t, , 亦可)
当即时,在x充分大时,h(x)<0,∴h(x)零点个数为1;
当即a=-3时,h(x)零点个数为2;
当即a<-3时,h(x)零点个数为3; …………13分
综上所述,当-3
x
y
o
y
x
o
x
y
o
o
y
x
是
否
输出S
结束
n=1,S=0
n≤5
开始
S=S+2n
n=n+1
(第10题)
A. B. C. D.
32
a
a
b
18
同课章节目录
