2021-2022学年冀教版七年级数学上册2.3 线段的长短 课件(共24张PPT)
文档属性
| 名称 | 2021-2022学年冀教版七年级数学上册2.3 线段的长短 课件(共24张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 7.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-19 20:49:11 | ||
图片预览







文档简介
(共24张PPT)
线段的长短
1、学会运用尺规作已知长度的线段;
2、掌握线段的比较的方法;
3、了解两点间距离的定义。
学习目标
掌握线段的比较方法。
重点
灵活运用两点间最短距离的数学知识。
难点
重难点
从上节课的所学知识中得出,线段具有可度量的特点,那么,我们如何画出一条指定长度的线段?或者说,如何画出一条与已知线段长度相等的线段?
我们可以先用直尺量出已知线段的长度,再画一条等于这个长度的线段。
思考
从上节课的所学知识中得出,线段具有可度量的特点,那么,我们如何画出一条指定长度的线段?或者说,如何画出一条与已知线段长度相等的线段?
那如果给你一个无刻度的直尺,你还能画出来么?
再加一个圆规呢?
思考
在数学中,我们常限定用无刻度的直尺和圆规作图,这就是尺规作图。
请利用无刻度直尺和圆规画出一条与已知线段长度相等的线段。
做一做
无刻度直尺和圆规的作用分别是什么?
在数学中,我们常限定用无刻度的直尺和圆规作图,这就是尺规作图。
请利用无刻度直尺和圆规画出一条与已知线段长度相等的线段。
做一做
直尺可以画出直线、射线、线段
圆规可以画圆,画弧,也可截取长度
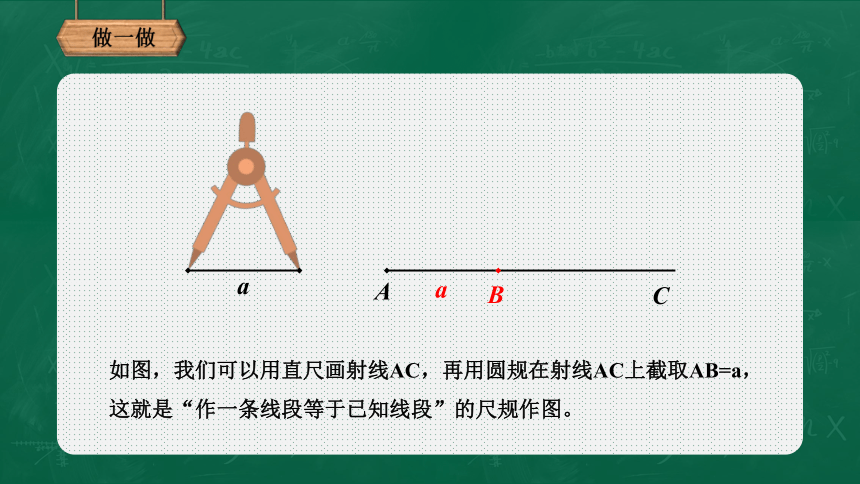
a
A
B
C
a
如图,我们可以用直尺画射线AC,再用圆规在射线AC上截取AB=a,这就是“作一条线段等于已知线段”的尺规作图。
做一做
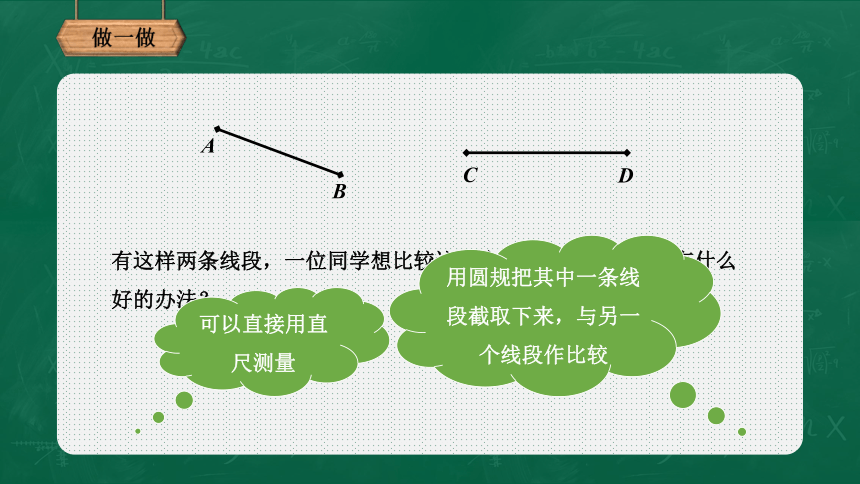
有这样两条线段,一位同学想比较这两个线段谁长谁短,你有什么好的办法?
可以直接用直尺测量
用圆规把其中一条线段截取下来,与另一个线段作比较
A
B
C
D
做一做
把其中的一条线段移到另一条上作比较:
A
B
C
D
B
(A)
做一做
点A与点C重合,点B落在C,D之间,这时我们说线段AB小于线段CD,记作AB
A
B
B
C
D
(A)
做一做
想一想:
什么情况下,线段AB大于线段CD,线段AB等于线段CD呢?
点B在点D的右侧时,AB>CD
点B与点D重合时,AB=CD
思考
做一做
如图,点P在线段AB上.
(1)在线段BA上,截取BQ=AP;
(2)延长AB至D,使BD=AP.
A
B
P
Q
D
如图,从A地到B地有四条道路,除它们外能否再修一条从A地到
B地的最短道路?如果能,请你联系以前所学的知识,在图上画出最短路。
距离
你能从中得出什么结论?
A
B
经过比较,我们可以得到一个关于线段的基本事实:
距离
连接两点间的线段的长度,叫做这两点的距离。
两点的所有连线中,线段最短。
你能举一些这条性质在生活中的实例吗?
下列四个生产生活现象,可以用基本事实“两点之间线段最短”来解释的是(
)
A.用两颗钉子就可以把木条钉在墙上
B.植树时,只要定出两棵树的位置,就能确定同一行树所在的直线
C.从A地到B地架设电线,总是尽可能沿着线段AB来架设
D.打靶的时候,眼睛要与枪上的准星、靶心在同一条直线上
C
练习
线段个数
A
B
在线段AB上增加1个点,则图中线段变为____________条;
在线段AB上增加2个点,则图中线段变为____________条;
在线段AB上增加3个点,则图中线段变为____________条;
在线段AB上增加n个点,则图中线段变为__________________条.
1+2
1+2+3
1+2+3+4
1+2+3+…+(n+1)
……
2.往返于A、B两地的客车,中途停靠C、D、E、F、G五个站,要准备______种车票.
1.如图:图中共有________条线段.
A
O
B
42
3
练习
1、如图,小明从家到学校分别有①、②、③三条路可走:①为折线段ABCDEFG,②为折线段AIG,③为折线段AJHG.三条路的长依次为a、b、c,则( )
A.a>b>c
B.a=b>c
C.a>c>b
D.a=b<c
B
基础巩固
2、如图,A、B两个村庄,在一条河
l(不计河的宽度)的两侧,现在要在河上建一座码头,使它到A、B两个村庄的距离之和最小,请你确定码头的位置,在图中用C点表示出来,并说明理由。
l
A
B
C
两点之间线段最短。
基础巩固
3、如图,AB+BC
AC,AC+BC
AB,AB+AC
BC(填“>”“<”或“=”).
其中蕴含的数学道理是___________________________.
>
>
>
两点之间线段最短
B
A
C
基础巩固
1、画线段:可通过直尺和圆规作已知长度的线段;
2、比较:度量法,可直接使用刻度尺测量线段的长度进行比较;叠合法,
将一线段“移动”,使其一端点与另一线段的一端点重合,两线段的另一端点均在同一射线上.
3、距离:两点之间,线段最短。
规律小结
运用尺规画已知长度的线段
知识
考点
线段的比较方法
课堂总结
两点间距离的定义
“两点之间,线段最短”的应用
线段的长短
1、学会运用尺规作已知长度的线段;
2、掌握线段的比较的方法;
3、了解两点间距离的定义。
学习目标
掌握线段的比较方法。
重点
灵活运用两点间最短距离的数学知识。
难点
重难点
从上节课的所学知识中得出,线段具有可度量的特点,那么,我们如何画出一条指定长度的线段?或者说,如何画出一条与已知线段长度相等的线段?
我们可以先用直尺量出已知线段的长度,再画一条等于这个长度的线段。
思考
从上节课的所学知识中得出,线段具有可度量的特点,那么,我们如何画出一条指定长度的线段?或者说,如何画出一条与已知线段长度相等的线段?
那如果给你一个无刻度的直尺,你还能画出来么?
再加一个圆规呢?
思考
在数学中,我们常限定用无刻度的直尺和圆规作图,这就是尺规作图。
请利用无刻度直尺和圆规画出一条与已知线段长度相等的线段。
做一做
无刻度直尺和圆规的作用分别是什么?
在数学中,我们常限定用无刻度的直尺和圆规作图,这就是尺规作图。
请利用无刻度直尺和圆规画出一条与已知线段长度相等的线段。
做一做
直尺可以画出直线、射线、线段
圆规可以画圆,画弧,也可截取长度
a
A
B
C
a
如图,我们可以用直尺画射线AC,再用圆规在射线AC上截取AB=a,这就是“作一条线段等于已知线段”的尺规作图。
做一做
有这样两条线段,一位同学想比较这两个线段谁长谁短,你有什么好的办法?
可以直接用直尺测量
用圆规把其中一条线段截取下来,与另一个线段作比较
A
B
C
D
做一做
把其中的一条线段移到另一条上作比较:
A
B
C
D
B
(A)
做一做
点A与点C重合,点B落在C,D之间,这时我们说线段AB小于线段CD,记作AB
A
B
B
C
D
(A)
做一做
想一想:
什么情况下,线段AB大于线段CD,线段AB等于线段CD呢?
点B在点D的右侧时,AB>CD
点B与点D重合时,AB=CD
思考
做一做
如图,点P在线段AB上.
(1)在线段BA上,截取BQ=AP;
(2)延长AB至D,使BD=AP.
A
B
P
Q
D
如图,从A地到B地有四条道路,除它们外能否再修一条从A地到
B地的最短道路?如果能,请你联系以前所学的知识,在图上画出最短路。
距离
你能从中得出什么结论?
A
B
经过比较,我们可以得到一个关于线段的基本事实:
距离
连接两点间的线段的长度,叫做这两点的距离。
两点的所有连线中,线段最短。
你能举一些这条性质在生活中的实例吗?
下列四个生产生活现象,可以用基本事实“两点之间线段最短”来解释的是(
)
A.用两颗钉子就可以把木条钉在墙上
B.植树时,只要定出两棵树的位置,就能确定同一行树所在的直线
C.从A地到B地架设电线,总是尽可能沿着线段AB来架设
D.打靶的时候,眼睛要与枪上的准星、靶心在同一条直线上
C
练习
线段个数
A
B
在线段AB上增加1个点,则图中线段变为____________条;
在线段AB上增加2个点,则图中线段变为____________条;
在线段AB上增加3个点,则图中线段变为____________条;
在线段AB上增加n个点,则图中线段变为__________________条.
1+2
1+2+3
1+2+3+4
1+2+3+…+(n+1)
……
2.往返于A、B两地的客车,中途停靠C、D、E、F、G五个站,要准备______种车票.
1.如图:图中共有________条线段.
A
O
B
42
3
练习
1、如图,小明从家到学校分别有①、②、③三条路可走:①为折线段ABCDEFG,②为折线段AIG,③为折线段AJHG.三条路的长依次为a、b、c,则( )
A.a>b>c
B.a=b>c
C.a>c>b
D.a=b<c
B
基础巩固
2、如图,A、B两个村庄,在一条河
l(不计河的宽度)的两侧,现在要在河上建一座码头,使它到A、B两个村庄的距离之和最小,请你确定码头的位置,在图中用C点表示出来,并说明理由。
l
A
B
C
两点之间线段最短。
基础巩固
3、如图,AB+BC
AC,AC+BC
AB,AB+AC
BC(填“>”“<”或“=”).
其中蕴含的数学道理是___________________________.
>
>
>
两点之间线段最短
B
A
C
基础巩固
1、画线段:可通过直尺和圆规作已知长度的线段;
2、比较:度量法,可直接使用刻度尺测量线段的长度进行比较;叠合法,
将一线段“移动”,使其一端点与另一线段的一端点重合,两线段的另一端点均在同一射线上.
3、距离:两点之间,线段最短。
规律小结
运用尺规画已知长度的线段
知识
考点
线段的比较方法
课堂总结
两点间距离的定义
“两点之间,线段最短”的应用
同课章节目录
- 第一章 有理数
- 1.1 正数和负数
- 1.2 数轴
- 1.3 绝对值与相反数
- 1.4 有理数的大小
- 1.5 有理数的加法
- 1.6 有理数的减法
- 1.7 有理数的加减混合运算
- 1.8 有理数的乘法
- 1.9 有理数的除法
- 1.10 有理数的乘方
- 1.11 有理数的混合运算
- 1.12 计算器的使用
- 第二章 几何图形的初步认识
- 2.1 从生活中认识几何图形
- 2.2 点和线
- 2.3 线段长短的比较
- 2.4 线段的和与差
- 2.5 角以及角的度量
- 2.6 角的大小
- 2.7 角的和与差
- 2.8 平面图形的旋转
- 第三章 代数式
- 3.1 用字母表示数
- 3.2 代数式
- 3.3 代数式的值
- 第四章 整式的加减
- 4.1 整式
- 4.2 合并同类项
- 4.3 去括号
- 4.4 整式的加减
- 第五章 一元一次方程
- 5.1一元一次方程
- 5.2 等式的基本性质
- 5.3 解一元一次方程
- 5.4 一元一次方程的应用
