2021-2022学年冀教版七年级数学上册2.7 角的和与差 课件(共25张PPT)
文档属性
| 名称 | 2021-2022学年冀教版七年级数学上册2.7 角的和与差 课件(共25张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 7.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-20 09:24:59 | ||
图片预览






文档简介
(共25张PPT)
角的和与差
1、理解角的和、差关系及角平分线的概念。
2、学会角的运算。
3、了解余角与补角的概念,理解余角与补角的性质并会进行运用
学习目标
角的和、差关系及角平分线的概念。
重点
角的运算。
难点
重难点
思考
如下图,图中共有几个角?它们之间有什么关系?
O
A
B
C
∠BOC
∠AOB
∠AOC
思考
O
A
B
C
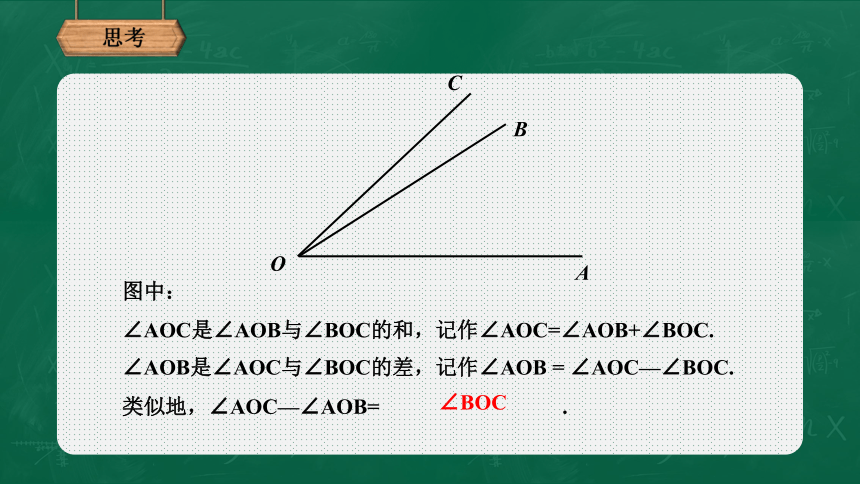
图中:
∠AOC是∠AOB与∠BOC的和,记作∠AOC=∠AOB+∠BOC.
∠AOB是∠AOC与∠BOC的差,记作∠AOB
=
∠AOC—∠BOC.
类似地,∠AOC—∠AOB=
.
∠BOC
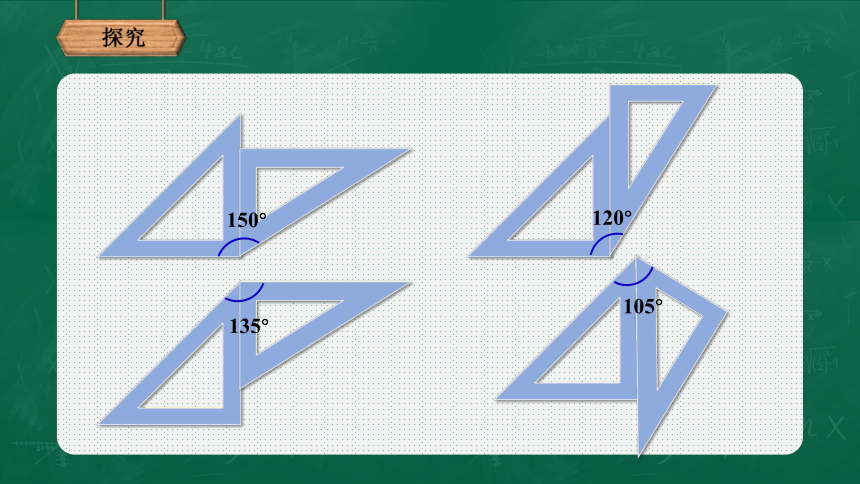
如下图,借助三角尺画出
15°、
75°的角。用一副三角尺,你还能画出哪些度数的角?试一试.
15°
75°
探究
135°
150°
120°
105°
探究
我们知道,线段的中点把线段分成相等的两条线段.
类似地,下图中,如果∠AOB=∠BOC,那么射线OB把∠AOC分成两个相等的角,这时有:
O
A
B
C
α
α
∠AOC
=
2∠AOB
=
2________,
∠AOB=∠BOC=
_________.
∠BOC
∠AOC
角平分线
O
A
B
C
α
α
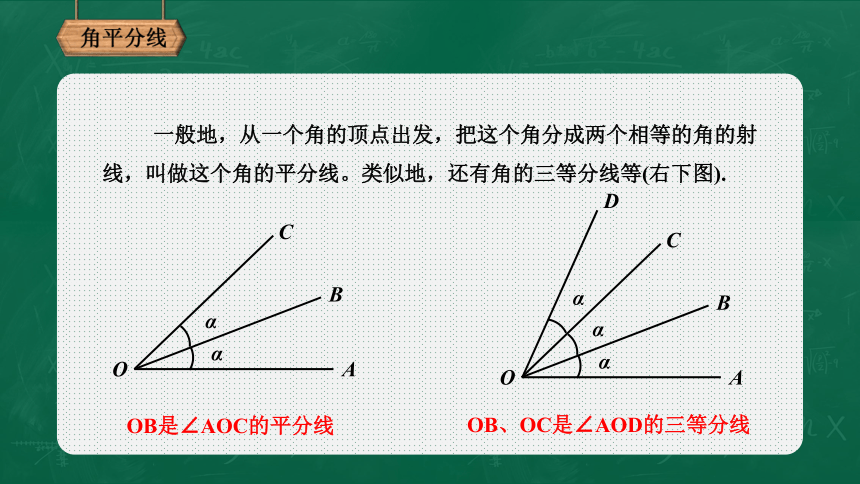
一般地,从一个角的顶点出发,把这个角分成两个相等的角的射线,叫做这个角的平分线。类似地,还有角的三等分线等(右下图).
O
A
B
C
α
α
α
D
OB是∠AOC的平分线
OB、OC是∠AOD的三等分线
角平分线
做一做
仿照下图,通过折纸作角平分线。
Q
P
R
Q
P
R
Q
P(R)
折痕即为角平分线
探究1
如图,如果∠AOC=∠DOB,那么∠AOD与∠COB相等吗?说明理由.
A
C
D
B
O
因为
∠AOC=∠DOB,
所以
∠AOC
+
∠COD
=∠DOB
+
∠COD
,
所以
∠AOD
=∠COB.
探究2
A
C
Q
B
O
P
如图,如果∠AOB=82°,OP是∠AOC的平分线,OQ是∠COB的平分线,请指明∠POQ的度数,说明理由。
∠POQ
=
∠POC
+
∠COQ
∠POQ
=
∠AOC
+
∠COB
∠POQ
=
(∠AOC
+
∠COB)
∠POQ
=
∠AOB
=
已知∠1=103°24′28″,∠2=30°54″,求∠1∠2和∠1∠2的度数。
∠1∠2
=
103°24′28″
+
30°54″
.
103°
24′
28″
30°
54″
+
133°
24′
82″
82″
=
1′22″
所以:∠1∠2
=
133°25′22″
例
已知∠1=103°24′28″,∠2=30°54″,求∠1∠2和∠1∠2的度数。
∠1∠2
=
103°24′28″
30°54″
.
103°
24′
28″
30°
54″
73°
23′
34″
24′28″
=
23′88″
所以:∠1∠2
=
73°23′34″
例
45°
45°
30°
60°
在一副三角尺中,每块都有一个角是90°,而其它两个角的和是90°。
一般地,如果两个角的和是90°,就说这两个角互为余角。
简称两角互余。
余角
1
2
1
2
∠1与∠2互为余角
其中∠1=18°,∠2=72°
∠1是∠2的余角;
∠2也是∠1的余角.
“互为”是什么意思?
这样的两角还是互为余角吗?
余角是表示角度的数量关系,与位置无关。
余角
如果两个角的和是180°(平角),就说这两个角互为补角。
简称两角互补。
补角
70°
110°
1
2
1
2
其中∠1=130°,∠2=50°
∠1与∠2互为补角
∠1是∠2的补角;
∠2也是∠1的补角.
这样的两角还是互为补角吗?
补角是表示角度的数量关系,与位置无关。
补角
互余
互补
相同点
都是表示角度的数量关系,与位置无关
不同点
两角互余,和为90°
两角互补,和为180°
对比
∠1与∠2,∠3都互为补角,∠2与∠3的大小有什么关系?
分析:∠1与∠2和∠3都互为补角,
所以∠2=∠3
由此,我们得到关于补角的一个性质:
那么∠2=180°-∠1,∠3=180°-∠1
同角(等角)的补角相等.
补角性质
若∠1与∠2,∠3都互为余角,∠2与∠3的大小有什么关系?
分析:∠1与∠2和∠3都互为余角,
所以∠2=∠3
由此,我们得到关于余角的一个性质:
同角(等角)的余角相等.
那么∠2=90°-∠1,∠3=90°-∠1
余角性质
基础巩固
1、一个角比它的余角大18°22′,则这个角的补角的度数为(
)
A.54°11′
B.125°49′
C.108°11′
D.35°49′
2、已知∠α和∠β互补,且∠α比∠β大70°,则∠α=______,∠β
=_______.
3、一个角的余角是补角的三分之一,则这个角的度数为________.
B
125°
55°
45°
随堂练习
4、如图,O是直线AB上一点,OC是∠AOB的平分线,∠COD
=
31°28′,
求∠AOD的度数.
=58°32′
A
B
O
D
C
解:由题意可知,∠AOB是平角,
由OC是∠AOB的平分线可知,
∠AOC=
∠AOB=
×180°
=
90°
由∠AOC=∠AOD+∠COD可知,
∠AOD=∠AOC—∠COD
=90°—31°28′
31°28′
余角和补角
知识
考点
利用角的运算及角平分线求角度
课堂总结
角的和、差关系及角平分线
利用余角和补角求角度
角的和与差
1、理解角的和、差关系及角平分线的概念。
2、学会角的运算。
3、了解余角与补角的概念,理解余角与补角的性质并会进行运用
学习目标
角的和、差关系及角平分线的概念。
重点
角的运算。
难点
重难点
思考
如下图,图中共有几个角?它们之间有什么关系?
O
A
B
C
∠BOC
∠AOB
∠AOC
思考
O
A
B
C
图中:
∠AOC是∠AOB与∠BOC的和,记作∠AOC=∠AOB+∠BOC.
∠AOB是∠AOC与∠BOC的差,记作∠AOB
=
∠AOC—∠BOC.
类似地,∠AOC—∠AOB=
.
∠BOC
如下图,借助三角尺画出
15°、
75°的角。用一副三角尺,你还能画出哪些度数的角?试一试.
15°
75°
探究
135°
150°
120°
105°
探究
我们知道,线段的中点把线段分成相等的两条线段.
类似地,下图中,如果∠AOB=∠BOC,那么射线OB把∠AOC分成两个相等的角,这时有:
O
A
B
C
α
α
∠AOC
=
2∠AOB
=
2________,
∠AOB=∠BOC=
_________.
∠BOC
∠AOC
角平分线
O
A
B
C
α
α
一般地,从一个角的顶点出发,把这个角分成两个相等的角的射线,叫做这个角的平分线。类似地,还有角的三等分线等(右下图).
O
A
B
C
α
α
α
D
OB是∠AOC的平分线
OB、OC是∠AOD的三等分线
角平分线
做一做
仿照下图,通过折纸作角平分线。
Q
P
R
Q
P
R
Q
P(R)
折痕即为角平分线
探究1
如图,如果∠AOC=∠DOB,那么∠AOD与∠COB相等吗?说明理由.
A
C
D
B
O
因为
∠AOC=∠DOB,
所以
∠AOC
+
∠COD
=∠DOB
+
∠COD
,
所以
∠AOD
=∠COB.
探究2
A
C
Q
B
O
P
如图,如果∠AOB=82°,OP是∠AOC的平分线,OQ是∠COB的平分线,请指明∠POQ的度数,说明理由。
∠POQ
=
∠POC
+
∠COQ
∠POQ
=
∠AOC
+
∠COB
∠POQ
=
(∠AOC
+
∠COB)
∠POQ
=
∠AOB
=
已知∠1=103°24′28″,∠2=30°54″,求∠1∠2和∠1∠2的度数。
∠1∠2
=
103°24′28″
+
30°54″
.
103°
24′
28″
30°
54″
+
133°
24′
82″
82″
=
1′22″
所以:∠1∠2
=
133°25′22″
例
已知∠1=103°24′28″,∠2=30°54″,求∠1∠2和∠1∠2的度数。
∠1∠2
=
103°24′28″
30°54″
.
103°
24′
28″
30°
54″
73°
23′
34″
24′28″
=
23′88″
所以:∠1∠2
=
73°23′34″
例
45°
45°
30°
60°
在一副三角尺中,每块都有一个角是90°,而其它两个角的和是90°。
一般地,如果两个角的和是90°,就说这两个角互为余角。
简称两角互余。
余角
1
2
1
2
∠1与∠2互为余角
其中∠1=18°,∠2=72°
∠1是∠2的余角;
∠2也是∠1的余角.
“互为”是什么意思?
这样的两角还是互为余角吗?
余角是表示角度的数量关系,与位置无关。
余角
如果两个角的和是180°(平角),就说这两个角互为补角。
简称两角互补。
补角
70°
110°
1
2
1
2
其中∠1=130°,∠2=50°
∠1与∠2互为补角
∠1是∠2的补角;
∠2也是∠1的补角.
这样的两角还是互为补角吗?
补角是表示角度的数量关系,与位置无关。
补角
互余
互补
相同点
都是表示角度的数量关系,与位置无关
不同点
两角互余,和为90°
两角互补,和为180°
对比
∠1与∠2,∠3都互为补角,∠2与∠3的大小有什么关系?
分析:∠1与∠2和∠3都互为补角,
所以∠2=∠3
由此,我们得到关于补角的一个性质:
那么∠2=180°-∠1,∠3=180°-∠1
同角(等角)的补角相等.
补角性质
若∠1与∠2,∠3都互为余角,∠2与∠3的大小有什么关系?
分析:∠1与∠2和∠3都互为余角,
所以∠2=∠3
由此,我们得到关于余角的一个性质:
同角(等角)的余角相等.
那么∠2=90°-∠1,∠3=90°-∠1
余角性质
基础巩固
1、一个角比它的余角大18°22′,则这个角的补角的度数为(
)
A.54°11′
B.125°49′
C.108°11′
D.35°49′
2、已知∠α和∠β互补,且∠α比∠β大70°,则∠α=______,∠β
=_______.
3、一个角的余角是补角的三分之一,则这个角的度数为________.
B
125°
55°
45°
随堂练习
4、如图,O是直线AB上一点,OC是∠AOB的平分线,∠COD
=
31°28′,
求∠AOD的度数.
=58°32′
A
B
O
D
C
解:由题意可知,∠AOB是平角,
由OC是∠AOB的平分线可知,
∠AOC=
∠AOB=
×180°
=
90°
由∠AOC=∠AOD+∠COD可知,
∠AOD=∠AOC—∠COD
=90°—31°28′
31°28′
余角和补角
知识
考点
利用角的运算及角平分线求角度
课堂总结
角的和、差关系及角平分线
利用余角和补角求角度
同课章节目录
- 第一章 有理数
- 1.1 正数和负数
- 1.2 数轴
- 1.3 绝对值与相反数
- 1.4 有理数的大小
- 1.5 有理数的加法
- 1.6 有理数的减法
- 1.7 有理数的加减混合运算
- 1.8 有理数的乘法
- 1.9 有理数的除法
- 1.10 有理数的乘方
- 1.11 有理数的混合运算
- 1.12 计算器的使用
- 第二章 几何图形的初步认识
- 2.1 从生活中认识几何图形
- 2.2 点和线
- 2.3 线段长短的比较
- 2.4 线段的和与差
- 2.5 角以及角的度量
- 2.6 角的大小
- 2.7 角的和与差
- 2.8 平面图形的旋转
- 第三章 代数式
- 3.1 用字母表示数
- 3.2 代数式
- 3.3 代数式的值
- 第四章 整式的加减
- 4.1 整式
- 4.2 合并同类项
- 4.3 去括号
- 4.4 整式的加减
- 第五章 一元一次方程
- 5.1一元一次方程
- 5.2 等式的基本性质
- 5.3 解一元一次方程
- 5.4 一元一次方程的应用
