2021-2022学年冀教版数学七年级上册第2章 几何图形初步认识 复习课件(共45张PPT)
文档属性
| 名称 | 2021-2022学年冀教版数学七年级上册第2章 几何图形初步认识 复习课件(共45张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 7.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-20 09:37:08 | ||
图片预览







文档简介
(共45张PPT)
几何初步
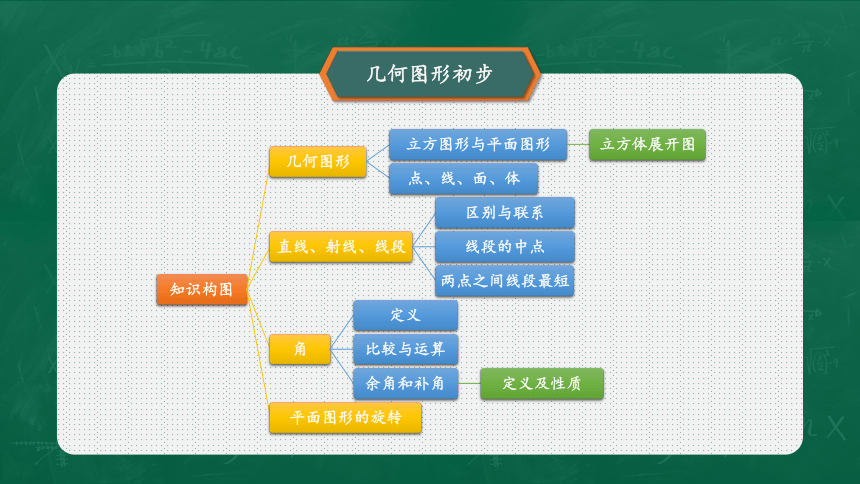
几何图形初步
几何图形
1、立体图形与平面图形
(1)像长方体、圆柱、圆锥、球等,都是立体图形.
(2)像线段、直线、三角形、长方形、圆等,都是平面图形.
2、几何图形的构成元素
(2)面与面相交成线,线分直线与曲线.
(1)包围着几何体的是面,面分平面和曲面.
(4)点、线、面是几何图形的基本要素.
(3)线与线相交成点.
几何图形
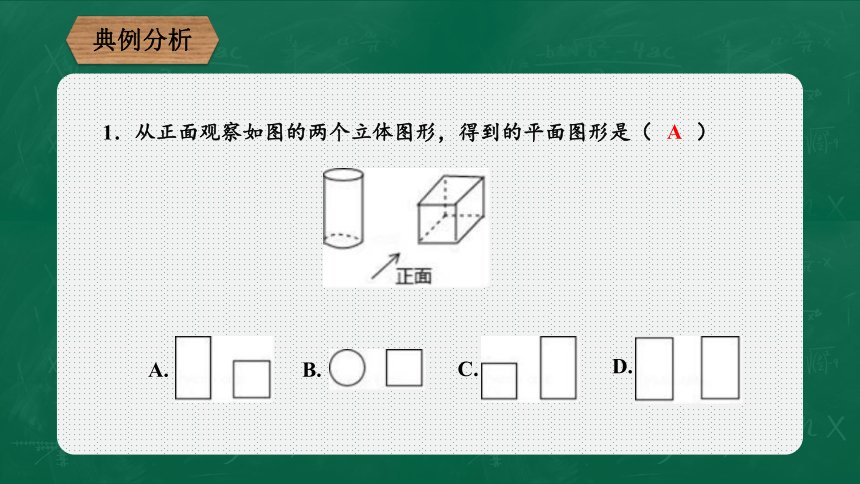
1.从正面观察如图的两个立体图形,得到的平面图形是( )
A.
B.
C.
D.
A
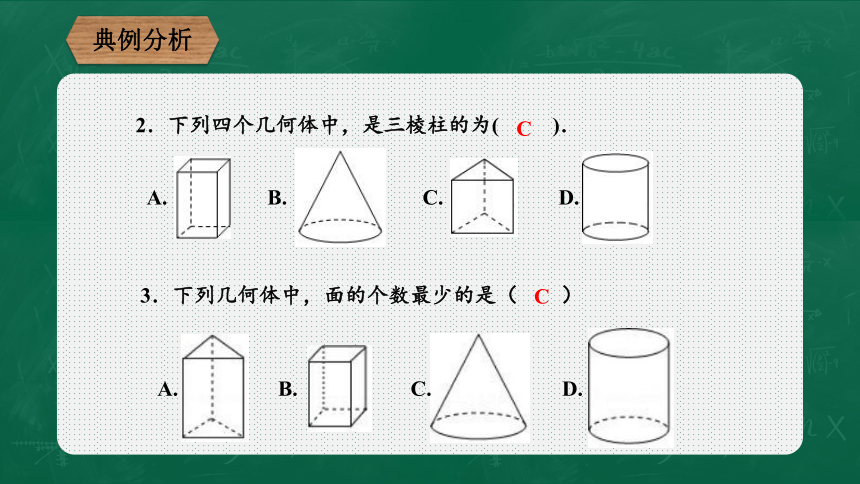
2.下列四个几何体中,是三棱柱的为(
).
A.
B.
C.
D.
3.下列几何体中,面的个数最少的是(
)
A.
B.
C.
D.
C
C
4.图中图形的周长是(
)米.
A.25.7
B.31.4
C.15.7
D.39.25
5.周长相等的圆、正方形和长方形,它们的面积比较(
).
A.正方形的面积大
B.圆的面积大
C.长方形的面积大
D.一样大
A
B
6.汽车的雨刷把玻璃上的雨水刷干净属于的实际应用是(
)
A.点动成线
B.线动成面
C.面动成体
D.以上答案都不对
B
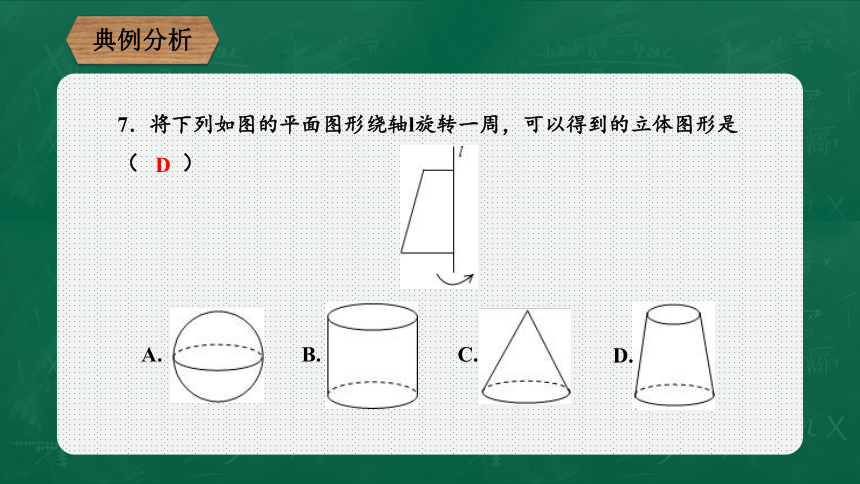
7.将下列如图的平面图形绕轴l旋转一周,可以得到的立体图形是( )
A.
B.
C.
D.
D
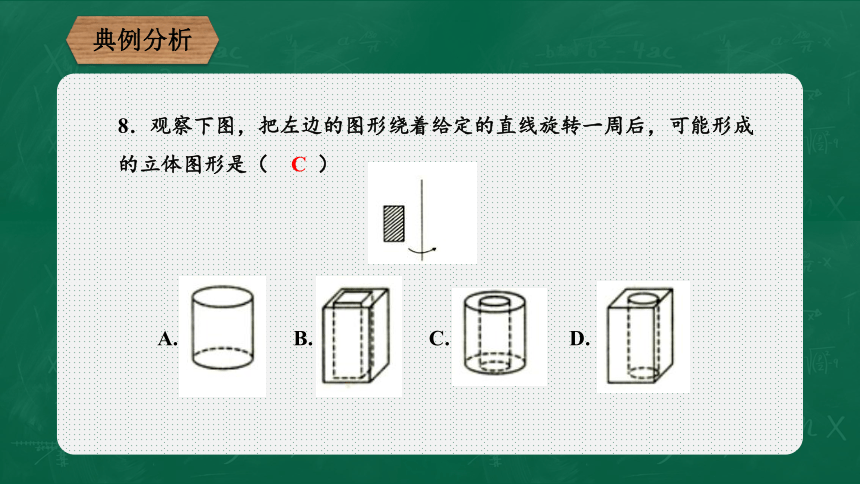
8.观察下图,把左边的图形绕着给定的直线旋转一周后,可能形成的立体图形是(?
?
)
A.
B.
C.
D.
C
10.如图,分割边长10cm的正方形,制作一副七巧板,图2是拼成的“小房子”,其中阴影部分的面积为_____cm2.
9.一个正方体中有一条棱是a,与a平行棱长有________?条,与a垂直并相交的棱长有________?条.
3
4
50
直线、射线、线段
1、线段、射线、直线的联系
名称
端点
延伸
表示
线段
线段有两个端点
可以向两个方向延伸
表示直线和线段的两个字母可以交换位置,而表示射线的两个字母不能交换位置.
射线
射线有一个端点
可以向一个方向延伸
直线
直线没有端点
直线不能再延伸
2、点与直线的两种位置关系
(2)点在直线外(直线不经过这个点).
(1)点在直线上(直线经过这个点);
3、直线的基本事实
经过两点有一条直线,并且只有一条直线.
4、线段的长短比较
(1)度量法;(2)叠合法.
5、线段的和差、中点
直线、射线、线段
6、线段的基本事实
8、尺规作图
两点之间的所有连线中,线段最短.
用圆规和没有刻度的直尺作图的方法叫做尺规作图.
7、两点之间线段的长度,叫做两点之间的距离.
直线、射线、线段
1.下列关于作图的语句中正确的是( )
A.画直线AB=10厘米
B.画射线OB=10厘米
C.已知A,B,C三点,过这三点画一条直线
D.过直线AB外一点画一条直线和直线AB平行
2.对于直线、射线、线段,在下列各图中能相交的是( )
A.
B.
C.
D.
D
B
3.下列说法中,正确的个数为(
)
①过同一平面内5点,最多可以确定9条直线;
②连接两点的线段叫做两点的距离;
③若,则点B是线段AC的中点;
④三条直线两两相交,一定有3个交点.
A.3个
B.2个
C.1个
D.0个
D
4.下列说法正确的个数是(
)
①射线MN与射线NM是同一条射线;
②两点确定一条直线;
③两点之间直线最短;
④若2AB=AC,则点B是AC的中点
A.1个
B.2个
C.3个
D.4个
A
5.如果点C在线段AB上,则下列各式中AC=AB,AC=CB,AB=2AC,AC+CB=AB,能说明C是线段AB中点的有(
)
A.1个
B.2个
C.3个
D.4个
6.两根木条,一根长20cm,另一根长30cm,将他们一端重合且放在同一条直线上,此时两根木条的中点之间的距离为(
)
A.5cm
B.10cm
C.5cm或25cm
D.10cm或50cm
C
C
7.已知线段AB,在AB的延长线上取一点C,使BC=AB;再在AB的反向延长线上取一点D,使DA=2AB,则下列结论错误的是( )
A.
C.
D.
B.
B
8.某工程队把一条弯曲的公路改为直道以达到缩短路程的目的,其道理用数学解释为(
)
A.两点之间,线段最短
B.两点确定一条直线
C.两点间的距离是指连接两点间的线段
D.点动成线
9.平面上A、B两点间的距离是指( )
A.经过A、B两点的直线
B.射线AB
C.A、B两点间的线段
D.A、B两点间线段长度
A
D
10.在同一平面内,若有4条直线,则最多有______个交点;若200条直线中恰好有且只有2m条直线互相平行,则这200条直线最多有_____________________个交点(用含有m的式子表示).
11.在线段AB上选取3种点,第1种是线段AB的中点,第2种是将线段AB三等分的点,第3种是将线段AB十等分的点.这些点连同线段AB的端点可组成线段的条数是_____.
6
78
12.如图,已知C,D为线段AB上顺次两点,点M,N分别为AC与BD的中点,若,则线段MN的长______.
24
13.如图,点C、D是线段AB上两点,点C分线段AD为1:3两部分,点D是线段CB的中点,
(1)求线段AC的长;
(2)求线段AB的长.
(1)AC=2;
(2)AB=14.
14.如图,点B在线段AC的延长线上,AC(1)若AC=8cm,CB=10cm,求线段MN的长;
(2)若AC=a,CB=b,求线段CD的长.
(1)9;
(2)
角
1、角的定义
(1)角是有公共端点的两条射线所组成的图形.这个公共端点叫做角的顶点,两条射线叫做角的边.
(2)角可以看做一条射线绕着端点旋转到另一个位置所形成的图形.
2、角的表示方法
表示方法
注意事项
用三个大写的字母表示
表示顶点的字母要写在中间
用一个顶点的字母来表示
只能是顶点只有两条射线时
用一个希腊字母(数字)表示
在靠近顶点处画上弧线,并写上希腊字母(数字)
角
3、角的度量与换算
把一个周角等分成360份,每份叫做1度,记做1°.
把1°的角等分成60份,每份叫做1分,记做1′;
再把1′的角等分成60份,每份叫做1秒,记做1″,
即1°=60′,1′=60″,1′=°,1″=′.
角
4、角的大小比较
(1)度量法;(2)叠合法.
5、角平分线
从一个角的顶点引出一条射线把这个角分成的两个角相等,那么这条射线叫这个角的平分线.
角
6、角的和与差
(1)余角:如果两个角的和等于____,那么说这两个角
互为余角(简称互余),也说其中一个角是另一个角的余角;
(2)补角:如果两个角的和等于____,那么说这两个角
互为补角(简称互补),也说其中一个角是另一个角的补角.
7、余角和补角的概念
8、余角和补角的性质
180°
90°
同角(或等角)的余角相等,同角(或等角)的补角相等.
角
9.平面图形的旋转
(1)在平面内,一个图形绕一个定点沿某个方向转过一个角度,这样的图形运动叫做旋转.这个定点叫做旋转中心,转过的这个角叫做旋转角.
角
(2)在平面内,一个图形旋转后得到的图形与原来的图形之间有如下结果:
①对应点到旋转中心的距离相等;
②每对对应点与旋转中心连线所成的角都是相等的角,它们都等于旋转角.
角
1.下列四个图中,能用∠1、∠AOB、∠O三种方法表示同一个角的是( )
A.
B.
C.
D.
D
2.有如下说法:①直线是一个平角;②如果线段AB=BC,则B是线段AC的中点;③射线AB与射线BA表示同一射线;④用一个扩大2倍的放大镜去看一个角,这个角扩大2倍;⑤两点之间,直线最短;⑥120.5°=120°30′,其中正确的有( )
A.1个
B.2个
C.3个
D.4个
A
3.将一副直角三角尺按如图所示摆放,图中锐角∠1的度数为(
)
A.58°
B.59°
C.60°
D.61°
C
4.如图,已知CO⊥AB于点O,∠AOD=5∠DOB+6°,则∠COD的度数(
)
A.58°
B.59°
C.60°
D.61°
5.若一个角为65°,则它的补角的度数为( )
A.25°
B.35°
C.115°
D.125°
D
C
6.已知:如图,,垂足为O,EF为过点O的一条直线,则与关系一定成立的是(
)
A.相等
B.互补
C.互余
D.互为对顶角
C
7.一副三角板按如图所示的方式摆放,且∠1比∠2大50°,则∠2的度数为( )
A.20°
B.50°
C.70°
D.30°
A
8.将一副直角三角尺如图放置,若∠BOC=160°,则∠AOD的大小为(
)
A.15°
B.20°
C.25°
D.30°
B
9.如图,小强从A处出发沿北偏东70°方向行走,走至B处,又沿着北偏西30°方向行走至C处,此时需把方向调整到与出发时一致,则方向的调整应是( )
A.左转
80°
B.右转80°
C.右转
100°
D.左转
100°
C
10.如图,OA方向是________________,∠AOB=________度.
北偏东60°
105
11.将一副直角三角板按图示方法放置(直角顶点重合),则___________________.
180°
12.将一副直角三角板ABC和DEF如图放置(其中∠A=60°,∠F=45°),使点E落在AC边上,且ED∥BC,则∠CEF的度数为_________.
15°
13.如图,过直线AB上一点O作射线OC,∠BOC=29°18′,则∠AOC的度数为_____________.
14.一个角的补角比它的余角的2倍还多20°,这个角的度数为__________.
150°42′
20°
15.如图,直线AB,CD相交于O,OE是∠AOD的平分线,∠AOC=28°,求∠AOE的度数.
∠AOE=76°
几何初步
几何图形初步
几何图形
1、立体图形与平面图形
(1)像长方体、圆柱、圆锥、球等,都是立体图形.
(2)像线段、直线、三角形、长方形、圆等,都是平面图形.
2、几何图形的构成元素
(2)面与面相交成线,线分直线与曲线.
(1)包围着几何体的是面,面分平面和曲面.
(4)点、线、面是几何图形的基本要素.
(3)线与线相交成点.
几何图形
1.从正面观察如图的两个立体图形,得到的平面图形是( )
A.
B.
C.
D.
A
2.下列四个几何体中,是三棱柱的为(
).
A.
B.
C.
D.
3.下列几何体中,面的个数最少的是(
)
A.
B.
C.
D.
C
C
4.图中图形的周长是(
)米.
A.25.7
B.31.4
C.15.7
D.39.25
5.周长相等的圆、正方形和长方形,它们的面积比较(
).
A.正方形的面积大
B.圆的面积大
C.长方形的面积大
D.一样大
A
B
6.汽车的雨刷把玻璃上的雨水刷干净属于的实际应用是(
)
A.点动成线
B.线动成面
C.面动成体
D.以上答案都不对
B
7.将下列如图的平面图形绕轴l旋转一周,可以得到的立体图形是( )
A.
B.
C.
D.
D
8.观察下图,把左边的图形绕着给定的直线旋转一周后,可能形成的立体图形是(?
?
)
A.
B.
C.
D.
C
10.如图,分割边长10cm的正方形,制作一副七巧板,图2是拼成的“小房子”,其中阴影部分的面积为_____cm2.
9.一个正方体中有一条棱是a,与a平行棱长有________?条,与a垂直并相交的棱长有________?条.
3
4
50
直线、射线、线段
1、线段、射线、直线的联系
名称
端点
延伸
表示
线段
线段有两个端点
可以向两个方向延伸
表示直线和线段的两个字母可以交换位置,而表示射线的两个字母不能交换位置.
射线
射线有一个端点
可以向一个方向延伸
直线
直线没有端点
直线不能再延伸
2、点与直线的两种位置关系
(2)点在直线外(直线不经过这个点).
(1)点在直线上(直线经过这个点);
3、直线的基本事实
经过两点有一条直线,并且只有一条直线.
4、线段的长短比较
(1)度量法;(2)叠合法.
5、线段的和差、中点
直线、射线、线段
6、线段的基本事实
8、尺规作图
两点之间的所有连线中,线段最短.
用圆规和没有刻度的直尺作图的方法叫做尺规作图.
7、两点之间线段的长度,叫做两点之间的距离.
直线、射线、线段
1.下列关于作图的语句中正确的是( )
A.画直线AB=10厘米
B.画射线OB=10厘米
C.已知A,B,C三点,过这三点画一条直线
D.过直线AB外一点画一条直线和直线AB平行
2.对于直线、射线、线段,在下列各图中能相交的是( )
A.
B.
C.
D.
D
B
3.下列说法中,正确的个数为(
)
①过同一平面内5点,最多可以确定9条直线;
②连接两点的线段叫做两点的距离;
③若,则点B是线段AC的中点;
④三条直线两两相交,一定有3个交点.
A.3个
B.2个
C.1个
D.0个
D
4.下列说法正确的个数是(
)
①射线MN与射线NM是同一条射线;
②两点确定一条直线;
③两点之间直线最短;
④若2AB=AC,则点B是AC的中点
A.1个
B.2个
C.3个
D.4个
A
5.如果点C在线段AB上,则下列各式中AC=AB,AC=CB,AB=2AC,AC+CB=AB,能说明C是线段AB中点的有(
)
A.1个
B.2个
C.3个
D.4个
6.两根木条,一根长20cm,另一根长30cm,将他们一端重合且放在同一条直线上,此时两根木条的中点之间的距离为(
)
A.5cm
B.10cm
C.5cm或25cm
D.10cm或50cm
C
C
7.已知线段AB,在AB的延长线上取一点C,使BC=AB;再在AB的反向延长线上取一点D,使DA=2AB,则下列结论错误的是( )
A.
C.
D.
B.
B
8.某工程队把一条弯曲的公路改为直道以达到缩短路程的目的,其道理用数学解释为(
)
A.两点之间,线段最短
B.两点确定一条直线
C.两点间的距离是指连接两点间的线段
D.点动成线
9.平面上A、B两点间的距离是指( )
A.经过A、B两点的直线
B.射线AB
C.A、B两点间的线段
D.A、B两点间线段长度
A
D
10.在同一平面内,若有4条直线,则最多有______个交点;若200条直线中恰好有且只有2m条直线互相平行,则这200条直线最多有_____________________个交点(用含有m的式子表示).
11.在线段AB上选取3种点,第1种是线段AB的中点,第2种是将线段AB三等分的点,第3种是将线段AB十等分的点.这些点连同线段AB的端点可组成线段的条数是_____.
6
78
12.如图,已知C,D为线段AB上顺次两点,点M,N分别为AC与BD的中点,若,则线段MN的长______.
24
13.如图,点C、D是线段AB上两点,点C分线段AD为1:3两部分,点D是线段CB的中点,
(1)求线段AC的长;
(2)求线段AB的长.
(1)AC=2;
(2)AB=14.
14.如图,点B在线段AC的延长线上,AC
(2)若AC=a,CB=b,求线段CD的长.
(1)9;
(2)
角
1、角的定义
(1)角是有公共端点的两条射线所组成的图形.这个公共端点叫做角的顶点,两条射线叫做角的边.
(2)角可以看做一条射线绕着端点旋转到另一个位置所形成的图形.
2、角的表示方法
表示方法
注意事项
用三个大写的字母表示
表示顶点的字母要写在中间
用一个顶点的字母来表示
只能是顶点只有两条射线时
用一个希腊字母(数字)表示
在靠近顶点处画上弧线,并写上希腊字母(数字)
角
3、角的度量与换算
把一个周角等分成360份,每份叫做1度,记做1°.
把1°的角等分成60份,每份叫做1分,记做1′;
再把1′的角等分成60份,每份叫做1秒,记做1″,
即1°=60′,1′=60″,1′=°,1″=′.
角
4、角的大小比较
(1)度量法;(2)叠合法.
5、角平分线
从一个角的顶点引出一条射线把这个角分成的两个角相等,那么这条射线叫这个角的平分线.
角
6、角的和与差
(1)余角:如果两个角的和等于____,那么说这两个角
互为余角(简称互余),也说其中一个角是另一个角的余角;
(2)补角:如果两个角的和等于____,那么说这两个角
互为补角(简称互补),也说其中一个角是另一个角的补角.
7、余角和补角的概念
8、余角和补角的性质
180°
90°
同角(或等角)的余角相等,同角(或等角)的补角相等.
角
9.平面图形的旋转
(1)在平面内,一个图形绕一个定点沿某个方向转过一个角度,这样的图形运动叫做旋转.这个定点叫做旋转中心,转过的这个角叫做旋转角.
角
(2)在平面内,一个图形旋转后得到的图形与原来的图形之间有如下结果:
①对应点到旋转中心的距离相等;
②每对对应点与旋转中心连线所成的角都是相等的角,它们都等于旋转角.
角
1.下列四个图中,能用∠1、∠AOB、∠O三种方法表示同一个角的是( )
A.
B.
C.
D.
D
2.有如下说法:①直线是一个平角;②如果线段AB=BC,则B是线段AC的中点;③射线AB与射线BA表示同一射线;④用一个扩大2倍的放大镜去看一个角,这个角扩大2倍;⑤两点之间,直线最短;⑥120.5°=120°30′,其中正确的有( )
A.1个
B.2个
C.3个
D.4个
A
3.将一副直角三角尺按如图所示摆放,图中锐角∠1的度数为(
)
A.58°
B.59°
C.60°
D.61°
C
4.如图,已知CO⊥AB于点O,∠AOD=5∠DOB+6°,则∠COD的度数(
)
A.58°
B.59°
C.60°
D.61°
5.若一个角为65°,则它的补角的度数为( )
A.25°
B.35°
C.115°
D.125°
D
C
6.已知:如图,,垂足为O,EF为过点O的一条直线,则与关系一定成立的是(
)
A.相等
B.互补
C.互余
D.互为对顶角
C
7.一副三角板按如图所示的方式摆放,且∠1比∠2大50°,则∠2的度数为( )
A.20°
B.50°
C.70°
D.30°
A
8.将一副直角三角尺如图放置,若∠BOC=160°,则∠AOD的大小为(
)
A.15°
B.20°
C.25°
D.30°
B
9.如图,小强从A处出发沿北偏东70°方向行走,走至B处,又沿着北偏西30°方向行走至C处,此时需把方向调整到与出发时一致,则方向的调整应是( )
A.左转
80°
B.右转80°
C.右转
100°
D.左转
100°
C
10.如图,OA方向是________________,∠AOB=________度.
北偏东60°
105
11.将一副直角三角板按图示方法放置(直角顶点重合),则___________________.
180°
12.将一副直角三角板ABC和DEF如图放置(其中∠A=60°,∠F=45°),使点E落在AC边上,且ED∥BC,则∠CEF的度数为_________.
15°
13.如图,过直线AB上一点O作射线OC,∠BOC=29°18′,则∠AOC的度数为_____________.
14.一个角的补角比它的余角的2倍还多20°,这个角的度数为__________.
150°42′
20°
15.如图,直线AB,CD相交于O,OE是∠AOD的平分线,∠AOC=28°,求∠AOE的度数.
∠AOE=76°
同课章节目录
- 第一章 有理数
- 1.1 正数和负数
- 1.2 数轴
- 1.3 绝对值与相反数
- 1.4 有理数的大小
- 1.5 有理数的加法
- 1.6 有理数的减法
- 1.7 有理数的加减混合运算
- 1.8 有理数的乘法
- 1.9 有理数的除法
- 1.10 有理数的乘方
- 1.11 有理数的混合运算
- 1.12 计算器的使用
- 第二章 几何图形的初步认识
- 2.1 从生活中认识几何图形
- 2.2 点和线
- 2.3 线段长短的比较
- 2.4 线段的和与差
- 2.5 角以及角的度量
- 2.6 角的大小
- 2.7 角的和与差
- 2.8 平面图形的旋转
- 第三章 代数式
- 3.1 用字母表示数
- 3.2 代数式
- 3.3 代数式的值
- 第四章 整式的加减
- 4.1 整式
- 4.2 合并同类项
- 4.3 去括号
- 4.4 整式的加减
- 第五章 一元一次方程
- 5.1一元一次方程
- 5.2 等式的基本性质
- 5.3 解一元一次方程
- 5.4 一元一次方程的应用
