2021—2022学年人教版九年级数学下册26.1.2反比例函数的图象和性质课件(第2课时,共26张PPT)
文档属性
| 名称 | 2021—2022学年人教版九年级数学下册26.1.2反比例函数的图象和性质课件(第2课时,共26张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 547.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-20 23:14:09 | ||
图片预览





文档简介
(共26张PPT)
第2课时
26.1.2
反比例函数的图象与性质
二四象限
一三象限
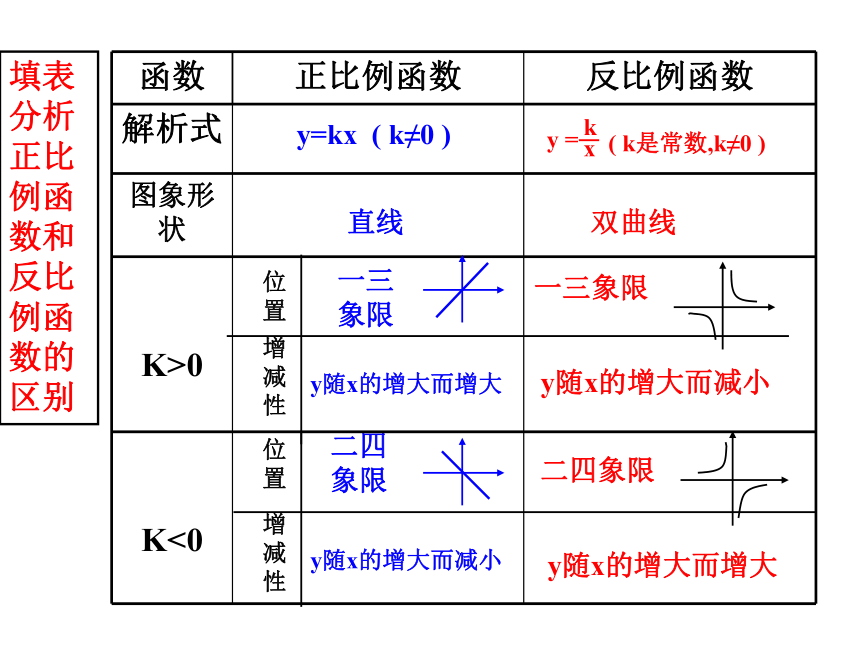
函数
正比例函数
反比例函数
解析式
图象形状
K>0
K<0
位置
增减性
位置
增减性
y=kx
(
k≠0
)
(
k是常数,k≠0
)
y
=
x
k
直线
双曲线
y随x的增大而增大
一三象限
y随x的增大而减小
二四象限
y随x的增大而减小
y随x的增大而增大
填表分析正比例函数和反比例函数的区别
例3:已知反比例函数的图象经过点A(2,6).
(1)这个函数的图象分布在哪些象限?y随x的增大如何变化?
(2)点B(3,4)、C(
)和D(2,5)是否在这个函数的图象上?
解:(1)设这个反比例函数为 ,
解得:
k=12
∴这个反比例函数的表达式为
∵k>0
∴这个函数的图象在第一、第三象限,
在每个象限内,y随x的增大而减小。
∵图象过点A(2,6)
(2)把点B、C和D的坐标代入 ,可知点B、
点C的坐标满足函数关系式,点D的坐标不满足函数关系式,
所以点B、点C在函数 的图象上,点D不在这个
函数的图象上。
例3:已知反比例函数的图象经过点A(2,6).
(1)这个函数的图象分布在哪些象限?y随x的增大如何变化?
(2)点B(3,4)、C(
)和D(2,5)是否在这个函数的图象上?
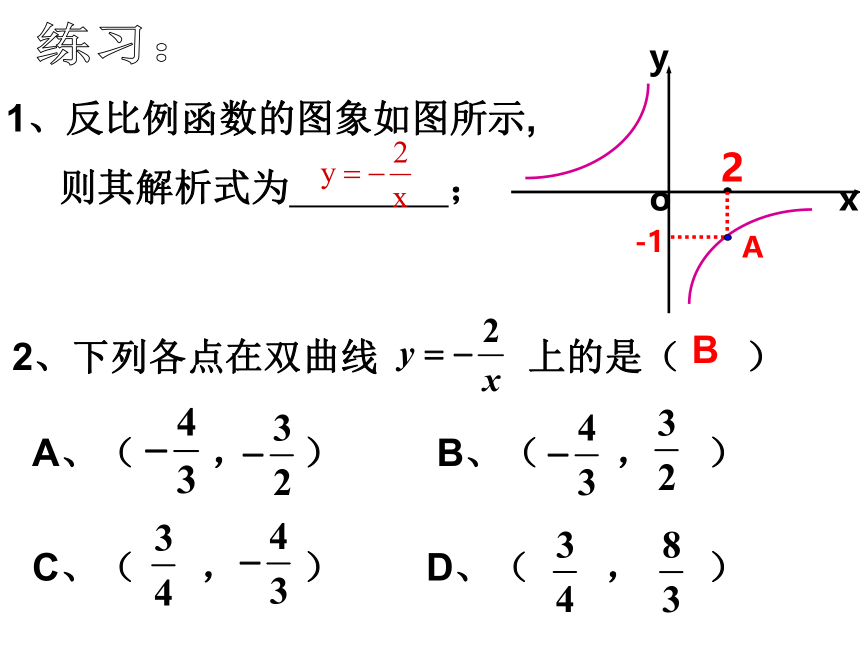
1、反比例函数的图象如图所示,
则其解析式为
;
y
x
o
2
-1
A
2、下列各点在双曲线
上的是(
)
A、(
,
)
B、(
,
)
C、(
,
)
D、(
,
)
B
3、反比例函数
的图象经过点(2,5),若点(1,n)在反比例函数图象上,则n等于(
)
A、10
B、5
C、2
D、-6
A
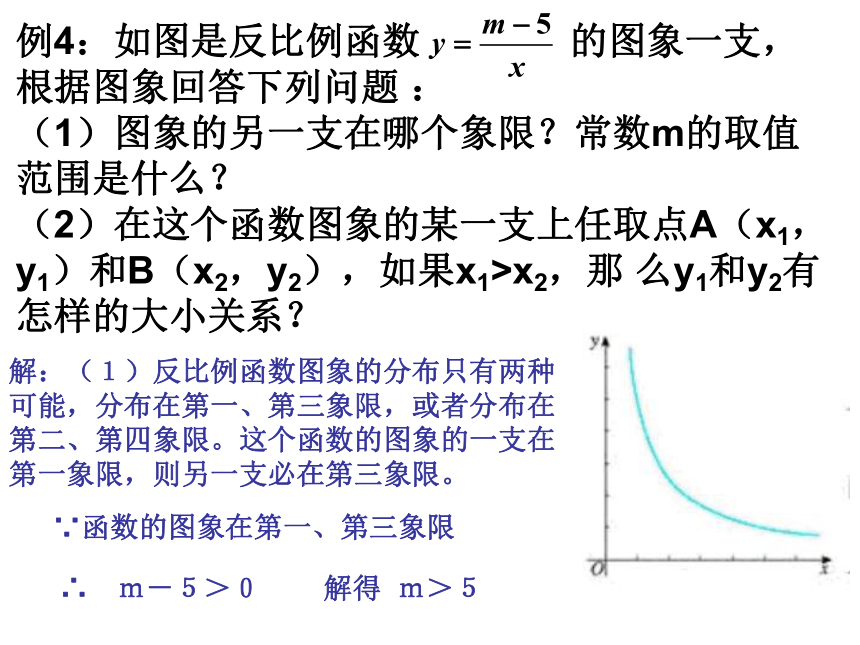
例4:如图是反比例函数
的图象一支,根据图象回答下列问题
:
(1)图象的另一支在哪个象限?常数m的取值范围是什么?
(2)在这个函数图象的某一支上任取点A(x1,y1)和B(x2,y2),如果x1>x2,那
么y1和y2有怎样的大小关系?
解:(1)反比例函数图象的分布只有两种可能,分布在第一、第三象限,或者分布在第二、第四象限。这个函数的图象的一支在第一象限,则另一支必在第三象限。
∵函数的图象在第一、第三象限
∴ m-5>0
解得
m>5
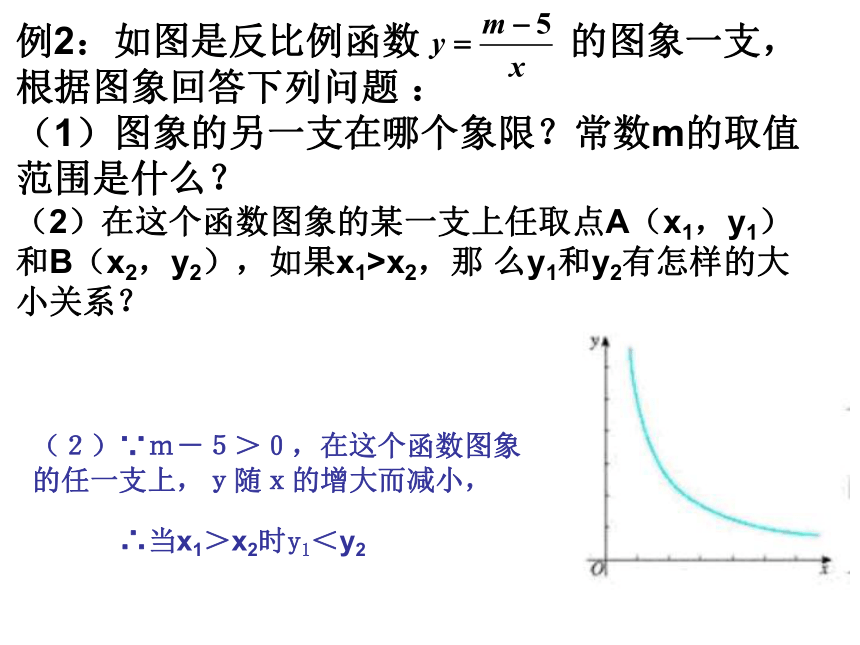
(2)∵m-5>0,在这个函数图象的任一支上,y随x的增大而减小,
∴当x1>x2时y1<y2
例2:如图是反比例函数
的图象一支,根据图象回答下列问题
:
(1)图象的另一支在哪个象限?常数m的取值范围是什么?
(2)在这个函数图象的某一支上任取点A(x1,y1)和B(x2,y2),如果x1>x2,那
么y1和y2有怎样的大小关系?
1.已知点A(-2,y1),B(-1,y2)
都在反比例函数
的图象上,则y1与
y2的大小关系为
.
(k>0)
y22.已知点
都在反比例函数
的图象上,则y1与y2的大小关系(从大到小)为
.
(k<0)
A(x1,y1),B(x2,y2)且x1<0<x2
y
x
o
x1
x2
A
y1
y2
B
y1
>0>y2
(1)反比例函数的增减性不是连续的,因此在
涉及反比例函数的增减性时,一般都是指在各自象限内的增减
情况.
(2)反比例函数图象的位置和函数的增减性,都是由反比例
系数
k
的符号决定的;反过来,由双曲线的位置和函数的增减
性,也可以推断出
k
的符号.
(3)解决反比例函数的相关问题时,往往我们需要画出函数
的大致图象(即草图)采用数形结合的方法,解决问题更直观.
P
D
o
y
x
1.如图,点P是反比例函数
图象上的一点,PD⊥x轴于D.则△POD的面积为
.
(m,n)
1
S△POD
= OD·PD
=
=
k
的几何意义(知识拓展)
2.如图,点P是反比例函数
图象上的一点,PA⊥x轴于A,
PB⊥y轴于B.则长方形PAOB的面积为
.
2
P(m,n)
A
o
y
x
B
S△POD
=OD·PD
=
=
P(m,n)
A
o
y
x
P(m,n)
A
o
y
x
归纳:面积性质(一)
P(m,n)
A
o
y
x
B
P(m,n)
A
o
y
x
B
面积性质(二)
1.如图,点P是反比例函数图象上的一点,过点P分别向x轴、y轴作垂线,若阴影部分面积为3,则这个反比例函数的
关系式是
.
x
y
o
M
N
p
2.
点P是反比例函数图象上的一点,过点P分别向x轴、y轴作垂线,若阴影部分面积为3,则这个反比例函数的
关系式是
.
3.一个反比例函数在第三象限如图所示,若A是图象上任意一点,AM⊥y轴于M,O是原点,如果△AOM的面积是3,那么这个反比例函数的解析式是什么?
o
y
x
A
M
S1
S2
如图:A、C是函数
的图象上任意两点,
A.S1>S2
B.S1C.S1
=
S2
D.S1和S2的大小关系不能确定.
C
A
B
o
y
x
C
D
D
S1
S2
A
A.S1
=
S2
=
S3
B.
S1
<
S2
<
S3
C.
S3
<
S1
<
S2
D.
S1
>
S2
>S3
B
A1
o
y
x
A
C
B1
C1
S1
S3
S2
4、如图,函数y=k/x和y=-kx+1(k≠0)在同一坐标系内的图象大致是
(
)
B
A
C
D
D
先假设某个函数
图象已经画好,
再确定另外的是否
符合条件.
若
,则函数
与
在同一平面直角坐标系中的图象大致是(
)
思维训练2
B
函数y=kx-k
与
在同一条直角坐标系中的
图象可能是
:
x
y
o
x
y
o
x
y
o
x
y
o
(A)
(B)
(C)
(D)
练一练
3
D
反比例函数的图象既是轴对称图形又是中心对称图形。
有两条对称轴:直线y=x和
y=-x。对称中心是:原点
x
y
0
1
2
y
=
—
k
x
y=x
y=-x
4、如图,已知反比例函数
的图象与一次函数
y=
kx+4的图象相交于P、Q两点,且P点的纵坐标
是6。
(1)求这个一次函数的解析式
(2)求三角形POQ的面积
x
y
o
P
Q
D
C
课外作业
课本第第9页第
6.7.8.9题.
第2课时
26.1.2
反比例函数的图象与性质
二四象限
一三象限
函数
正比例函数
反比例函数
解析式
图象形状
K>0
K<0
位置
增减性
位置
增减性
y=kx
(
k≠0
)
(
k是常数,k≠0
)
y
=
x
k
直线
双曲线
y随x的增大而增大
一三象限
y随x的增大而减小
二四象限
y随x的增大而减小
y随x的增大而增大
填表分析正比例函数和反比例函数的区别
例3:已知反比例函数的图象经过点A(2,6).
(1)这个函数的图象分布在哪些象限?y随x的增大如何变化?
(2)点B(3,4)、C(
)和D(2,5)是否在这个函数的图象上?
解:(1)设这个反比例函数为 ,
解得:
k=12
∴这个反比例函数的表达式为
∵k>0
∴这个函数的图象在第一、第三象限,
在每个象限内,y随x的增大而减小。
∵图象过点A(2,6)
(2)把点B、C和D的坐标代入 ,可知点B、
点C的坐标满足函数关系式,点D的坐标不满足函数关系式,
所以点B、点C在函数 的图象上,点D不在这个
函数的图象上。
例3:已知反比例函数的图象经过点A(2,6).
(1)这个函数的图象分布在哪些象限?y随x的增大如何变化?
(2)点B(3,4)、C(
)和D(2,5)是否在这个函数的图象上?
1、反比例函数的图象如图所示,
则其解析式为
;
y
x
o
2
-1
A
2、下列各点在双曲线
上的是(
)
A、(
,
)
B、(
,
)
C、(
,
)
D、(
,
)
B
3、反比例函数
的图象经过点(2,5),若点(1,n)在反比例函数图象上,则n等于(
)
A、10
B、5
C、2
D、-6
A
例4:如图是反比例函数
的图象一支,根据图象回答下列问题
:
(1)图象的另一支在哪个象限?常数m的取值范围是什么?
(2)在这个函数图象的某一支上任取点A(x1,y1)和B(x2,y2),如果x1>x2,那
么y1和y2有怎样的大小关系?
解:(1)反比例函数图象的分布只有两种可能,分布在第一、第三象限,或者分布在第二、第四象限。这个函数的图象的一支在第一象限,则另一支必在第三象限。
∵函数的图象在第一、第三象限
∴ m-5>0
解得
m>5
(2)∵m-5>0,在这个函数图象的任一支上,y随x的增大而减小,
∴当x1>x2时y1<y2
例2:如图是反比例函数
的图象一支,根据图象回答下列问题
:
(1)图象的另一支在哪个象限?常数m的取值范围是什么?
(2)在这个函数图象的某一支上任取点A(x1,y1)和B(x2,y2),如果x1>x2,那
么y1和y2有怎样的大小关系?
1.已知点A(-2,y1),B(-1,y2)
都在反比例函数
的图象上,则y1与
y2的大小关系为
.
(k>0)
y2
都在反比例函数
的图象上,则y1与y2的大小关系(从大到小)为
.
(k<0)
A(x1,y1),B(x2,y2)且x1<0<x2
y
x
o
x1
x2
A
y1
y2
B
y1
>0>y2
(1)反比例函数的增减性不是连续的,因此在
涉及反比例函数的增减性时,一般都是指在各自象限内的增减
情况.
(2)反比例函数图象的位置和函数的增减性,都是由反比例
系数
k
的符号决定的;反过来,由双曲线的位置和函数的增减
性,也可以推断出
k
的符号.
(3)解决反比例函数的相关问题时,往往我们需要画出函数
的大致图象(即草图)采用数形结合的方法,解决问题更直观.
P
D
o
y
x
1.如图,点P是反比例函数
图象上的一点,PD⊥x轴于D.则△POD的面积为
.
(m,n)
1
S△POD
= OD·PD
=
=
k
的几何意义(知识拓展)
2.如图,点P是反比例函数
图象上的一点,PA⊥x轴于A,
PB⊥y轴于B.则长方形PAOB的面积为
.
2
P(m,n)
A
o
y
x
B
S△POD
=OD·PD
=
=
P(m,n)
A
o
y
x
P(m,n)
A
o
y
x
归纳:面积性质(一)
P(m,n)
A
o
y
x
B
P(m,n)
A
o
y
x
B
面积性质(二)
1.如图,点P是反比例函数图象上的一点,过点P分别向x轴、y轴作垂线,若阴影部分面积为3,则这个反比例函数的
关系式是
.
x
y
o
M
N
p
2.
点P是反比例函数图象上的一点,过点P分别向x轴、y轴作垂线,若阴影部分面积为3,则这个反比例函数的
关系式是
.
3.一个反比例函数在第三象限如图所示,若A是图象上任意一点,AM⊥y轴于M,O是原点,如果△AOM的面积是3,那么这个反比例函数的解析式是什么?
o
y
x
A
M
S1
S2
如图:A、C是函数
的图象上任意两点,
A.S1>S2
B.S1
=
S2
D.S1和S2的大小关系不能确定.
C
A
B
o
y
x
C
D
D
S1
S2
A
A.S1
=
S2
=
S3
B.
S1
<
S2
<
S3
C.
S3
<
S1
<
S2
D.
S1
>
S2
>S3
B
A1
o
y
x
A
C
B1
C1
S1
S3
S2
4、如图,函数y=k/x和y=-kx+1(k≠0)在同一坐标系内的图象大致是
(
)
B
A
C
D
D
先假设某个函数
图象已经画好,
再确定另外的是否
符合条件.
若
,则函数
与
在同一平面直角坐标系中的图象大致是(
)
思维训练2
B
函数y=kx-k
与
在同一条直角坐标系中的
图象可能是
:
x
y
o
x
y
o
x
y
o
x
y
o
(A)
(B)
(C)
(D)
练一练
3
D
反比例函数的图象既是轴对称图形又是中心对称图形。
有两条对称轴:直线y=x和
y=-x。对称中心是:原点
x
y
0
1
2
y
=
—
k
x
y=x
y=-x
4、如图,已知反比例函数
的图象与一次函数
y=
kx+4的图象相交于P、Q两点,且P点的纵坐标
是6。
(1)求这个一次函数的解析式
(2)求三角形POQ的面积
x
y
o
P
Q
D
C
课外作业
课本第第9页第
6.7.8.9题.
