2021-2022学年湘教版七年级上数学1.4有理数的加法和减法 同步练习(word解析版)
文档属性
| 名称 | 2021-2022学年湘教版七年级上数学1.4有理数的加法和减法 同步练习(word解析版) |

|
|
| 格式 | docx | ||
| 文件大小 | 99.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-19 00:00:00 | ||
图片预览



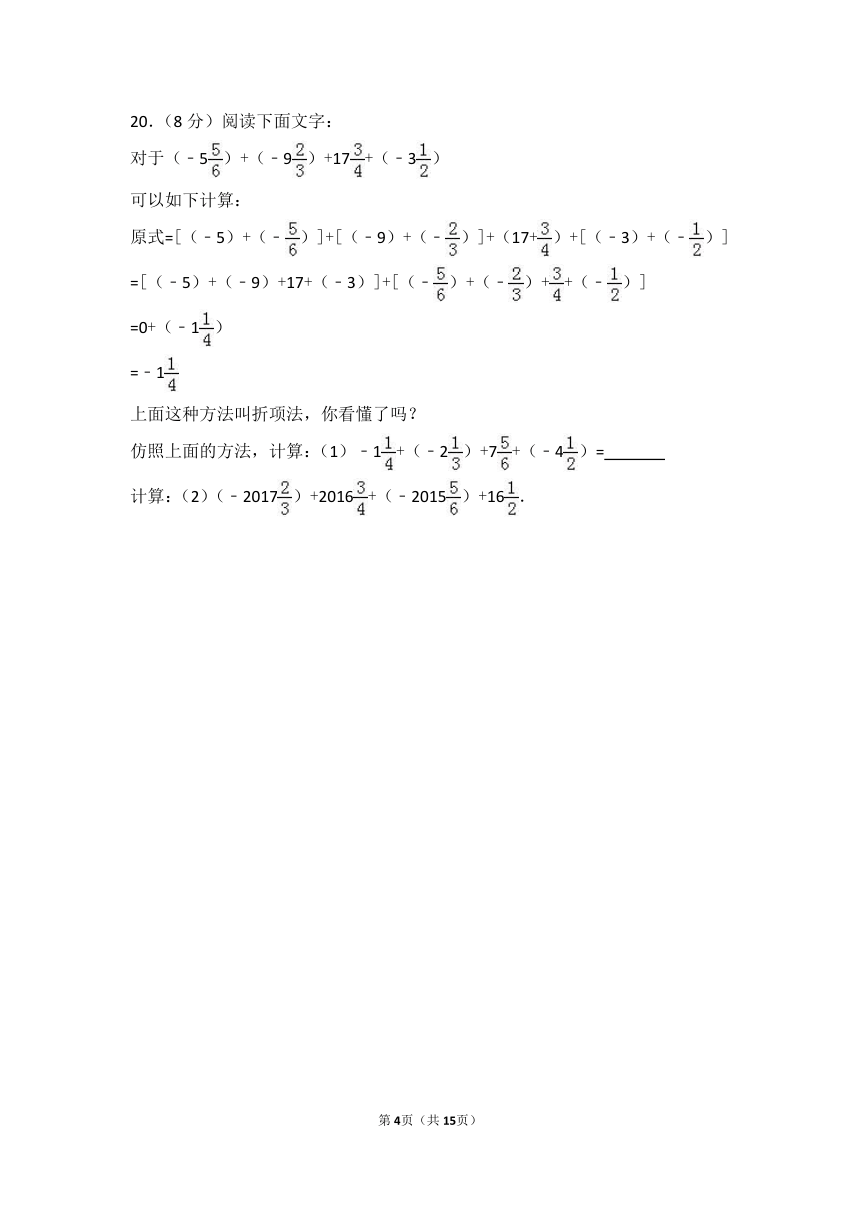

文档简介
《1.4有理数的加法和减法》同步练习
一、选择题(
本大题共10小题,共40.0分)
1.(4分)设a为最小的正整数,b为最大的负整数,c是绝对值最小的有理数,则a+b﹣c的值为( )
A.0
B.2
C.﹣2
D.2或﹣2
2.(4分)若a<0,b>0,且|a|<|b|,则a+b的值一定是( )
A.正数
B.负数
C.0
D.非负数
3.(4分)若|x|=3,|y|=4,则|x+y|的值为( )
A.7
B.﹣7
C.7或1
D.以上都不对
4.(4分)如果a+b+c=0,且|c|>|b|>|a|,则下列说法中可能成立的是( )
A.a、b为正数,c为负数
B.a、c为正数,b为负数
C.b、c为正数,a为负数
D.a、c为正数,b为负数
5.(4分)计算1﹣3+5﹣7+9=(1+5+9)+(﹣3﹣7)是应用了( )
A.加法交换律
B.加法结合律
C.分配律
D.加法交换律与结合律
6.(4分)|a|+|b|=|a+b|,则a,b关系是( )
A.a,b的绝对值相等
B.a,b异号
C.a+b的和是非负数
D.a、b同号或a、b其中一个为0
7.(4分)如表为蒙城县2018年某日天气预报信息,根据图表可知当天最高气温比最低气温高了( )
2018年1月6日蒙城天气预报
天气现象
气温
1月6日
星期六
白天
晴
高温7℃
夜间
晴
低温﹣5℃
A.2℃
B.﹣2℃
C.12℃
D.﹣12℃
8.(4分)已知x=1,|y|=2且x>y,则x﹣y的值是( )
A.﹣1
B.﹣3
C.1
D.3
9.(4分)如图表格是一个4×4的奇妙方阵;
从这个方阵中选四个数(其中任何两个既不在同一行,也不在同一列),虽然有很多种选法,但每次选出的四个数相加,其和是一个定值.则方阵中空白处的数是( )
A.5
B.6
C.7
D.8
10.(4分)如图,从左到右在每个小格子中填入一个整数,使得其中任意三个相邻格子中所填整数之和都相等.若前m个格子中所填整数之和是1684,则m的值可以是( )
A.1015
B.1010
C.1012
D.1018
二、填空题(
本大题共5小题,共20.0分)
11.(4分)已知,|a|=﹣a,=﹣1,|c|=c,化简|a+b|﹣|a﹣c|﹣|b﹣c|=
.
12.(4分)在数A的右端再加上一个数字6,则该数比原数增加2004,那么A=
.
13.(4分)若x2=9,|y|=4且x<y,则x+y=
.
14.(4分)若|a|=8,|b|=3,则当a与b异号时,a+b=
.
15.(4分)若|a|=6,|b|=2,且|a+b|=a+b,则a﹣b的值
.
三、解答题(
本大题共5小题,共40.0分)
16.(8分)观察下面的等式:
﹣1=﹣|﹣+2|+3;
3﹣1=﹣|﹣1+2|+3;
1﹣1=﹣|1+2|+3;
(﹣)﹣1=﹣|+2|+3;
(﹣2)﹣1=﹣|4+2|+3
回答下列问题:
(1)填空:
﹣1=﹣|5+2|+3;
(2)已知2﹣1=﹣|x+2|+3,则x的值是
;
(3)设满足上面特征的等式最左边的数为y,求y的最大值,并写出此时的等式.
17.(8分)在解决数学问题的过程中,我们常用到“分类讨论”的数学思想,下面是运用分类讨论的数学思想解决问题的过程,请仔细阅读,并解答题目后提出的【探究】.
【提出问题】两个有理数a、b满足a、b同号,求+的值.
【解决问题】
解:由a、b同号,可知a、b有两种可能:①当a,b都正数;②当a,b都是负数.①若a、b都是正数,即a>0,b>0,有|a|=a,|b|=b,则+=+=1+1=2;②若a、b都是负数,即a<0,b<0,有|a|=﹣a,|b|=﹣b,则+=+=(﹣1)+(﹣1)=﹣2,所以+的值为2或﹣2.
【探究】请根据上面的解题思路解答下面的问题:
(1)两个有理数a、b满足a、b异号,求+的值;
(2)已知|a|=3,|b|=7,且a<b,求a+b的值.
18.(8分)在一个3×3的方格中填写了9个数字,使得每行、每列、每条对角线上的三个数之和相等,得到的3×3的方格称为一个三阶幻方.
(1)在图1中空格处填上合适的数字,使它构成一个三阶幻方;
(2)如图2的方格中填写了一些数和字母,当x+y的值为多少时,它能构成一个三阶幻方.
19.(8分)已知a是最小的正整数,b是最大的负整数,c是绝对值最小的有理数,表示有理数d的点到原点的距离为4,求a﹣b﹣c+d的值.
20.(8分)阅读下面文字:
对于(﹣5)+(﹣9)+17+(﹣3)
可以如下计算:
原式=[(﹣5)+(﹣)]+[(﹣9)+(﹣)]+(17+)+[(﹣3)+(﹣)]
=[(﹣5)+(﹣9)+17+(﹣3)]+[(﹣)+(﹣)++(﹣)]
=0+(﹣1)
=﹣1
上面这种方法叫折项法,你看懂了吗?
仿照上面的方法,计算:(1)﹣1+(﹣2)+7+(﹣4)=
计算:(2)(﹣2017)+2016+(﹣2015)+16.
参考答案与试题解析
一、选择题(
本大题共10小题,共40.0分)
1.(4分)设a为最小的正整数,b为最大的负整数,c是绝对值最小的有理数,则a+b﹣c的值为( )
A.0
B.2
C.﹣2
D.2或﹣2
【分析】由a为最小的正整数,b为最大的负整数,c是绝对值最小的有理数,可分别得出a、b、c的值,代入计算可得结果.
【解答】解:根据题意知a=1,b=﹣1,c=0,
则a+b﹣c=1﹣1+0=0,
故选:A.
【点评】本题主要考查有理数的概念的理解,能正确判断有关有理数的概念是解题的关键.
2.(4分)若a<0,b>0,且|a|<|b|,则a+b的值一定是( )
A.正数
B.负数
C.0
D.非负数
【分析】根据题意,利用绝对值的代数意义,以及有理数的加法法则判断即可.
【解答】解:∵a<0,b>0,且|a|<|b|,
∴a+b的值一定是正数,
故选:A.
【点评】本题主要考查有理数的加法,在进行有理数加法运算时,首先判断两个加数的符号:是同号还是异号,是否有0.从而确定用那一条法则.在应用过程中,要牢记“先符号,后绝对值”.
3.(4分)若|x|=3,|y|=4,则|x+y|的值为( )
A.7
B.﹣7
C.7或1
D.以上都不对
【分析】根据绝对值的性质进行分类讨论计算即可.
【解答】解:由|x|=3,|y|=4
可得
x=±3,y=±4,
所以|x+y|=|3+4|=7,或|x+y|=|﹣3﹣4|=7,或|x+y|=|3﹣4|=1,或|x+y|=|﹣3+4|=1
综上所述|x+y|的值为7或1.
故选:C.
【点评】此题主要考查与绝对值有关的计算,根据绝对值的性质合理全面的进行分类是解题的关键.
4.(4分)如果a+b+c=0,且|c|>|b|>|a|,则下列说法中可能成立的是( )
A.a、b为正数,c为负数
B.a、c为正数,b为负数
C.b、c为正数,a为负数
D.a、c为正数,b为负数
【分析】根据有理数的加法,一对相反数的和为0,可得a、b、c中至少有一个为正数,至少有一个为负数,又|c|>|b|>|a|,那么|c|=|b|+|a|,进而得出可能存在的情况.
【解答】解:∵a+b+c=0,
∴a、b、c中至少有一个为正数,至少有一个为负数,
∵|c|>|b|>|a|,
∴|c|=|b|+|a|,
∴可能a、b为正数,c为负数;也可能a、b为负数,c为正数.
故选:A.
【点评】本题主要考查的是有理数的加法,绝对值的意义,掌握有理数的加法法则是解题的关键.
5.(4分)计算1﹣3+5﹣7+9=(1+5+9)+(﹣3﹣7)是应用了( )
A.加法交换律
B.加法结合律
C.分配律
D.加法交换律与结合律
【分析】根据加法交换律与结合律即可求解.
【解答】解:计算1﹣3+5﹣7+9=(1+5+9)+(﹣3﹣7)是应用了加法交换律与结合律.
故选:D.
【点评】考查了有理数的加减混合运算,方法指引:①在一个式子里,有加法也有减法,根据有理数减法法则,把减法都转化成加法,并写成省略括号的和的形式.
②转化成省略括号的代数和的形式,就可以应用加法的运算律,使计算简化.
6.(4分)|a|+|b|=|a+b|,则a,b关系是( )
A.a,b的绝对值相等
B.a,b异号
C.a+b的和是非负数
D.a、b同号或a、b其中一个为0
【分析】每一种情况都举出例子,再判断即可.
【解答】解:A、当a、b的绝对值相等时,如a=1,b=﹣1,|a|+|b|=2,|a+b|=0,即|a|+|b|≠|a+b|,故本选项不符合题意;
B、当a、b异号时,如a=1,b=﹣3,|a|+|b|=4,|a+b|=2,即|a|+|b|≠|a+b|,故本选项不符合题意;
C、当a+b的和是非负数时,如:a=﹣1,b=3,|a|+|b|=4,|a+b|=2,即即|a|+|b|≠|a+b|,故本选项不符合题意;
D、当a、b同号或a、b其中一个为0时,|a|+|b|=|a+b|,故本选项符合题意;
故选:D.
【点评】本题考查了绝对值、有理数的加法等知识点,能根据选项举出反例是解此题的关键.
7.(4分)如表为蒙城县2018年某日天气预报信息,根据图表可知当天最高气温比最低气温高了( )
2018年1月6日蒙城天气预报
天气现象
气温
1月6日
星期六
白天
晴
高温7℃
夜间
晴
低温﹣5℃
A.2℃
B.﹣2℃
C.12℃
D.﹣12℃
【分析】用最高气温减去最低气温,列出算式计算即可求解.
【解答】解:7﹣(﹣5)=12(℃).
故选:C.
【点评】此题主要考查了有理数的减法,关键是掌握有理数减法法则:减去一个数,等于加上这个数的相反数.
8.(4分)已知x=1,|y|=2且x>y,则x﹣y的值是( )
A.﹣1
B.﹣3
C.1
D.3
【分析】根据题意,利用绝对值的代数意义求出y的值,即可求出x﹣y的值.
【解答】解:∵x=1,|y|=2且x>y,
∴x=1,y=﹣2,
则x﹣y=3.
故选:D.
【点评】此题考查了代数式求值,绝对值,熟练掌握运算法则是解本题的关键.
9.(4分)如图表格是一个4×4的奇妙方阵;
从这个方阵中选四个数(其中任何两个既不在同一行,也不在同一列),虽然有很多种选法,但每次选出的四个数相加,其和是一个定值.则方阵中空白处的数是( )
A.5
B.6
C.7
D.8
【分析】设空白处的数为x,根据“每次选出的四个数相加,其和是一个定值”可得1﹣2+x+6=4﹣1+6+3,解之即可.
【解答】解:设空白处的数为x,
则1﹣2+x+6=4﹣1+6+3,
解得:x=7,
故选:C.
【点评】本题主要考查一元一次方程,解题的关键是理解题意列出关于空白处数字的方程.
10.(4分)如图,从左到右在每个小格子中填入一个整数,使得其中任意三个相邻格子中所填整数之和都相等.若前m个格子中所填整数之和是1684,则m的值可以是( )
A.1015
B.1010
C.1012
D.1018
【分析】根据题意可求得c=9,然后求得9+(﹣5)+1=5,然后按照规律可求得m的值.
【解答】解:由题意可知:9+a+b=a+b+c,
∴c=9.
∵9﹣5+1=5,
1684÷5=336…4,
且9﹣5=4,
∴m=336×3+2=1010.
故选:B.
【点评】此题考查数字的变化规律,找出数字之间的联系得出规律是解决问题的关键.
二、填空题(
本大题共5小题,共20.0分)
11.(4分)已知,|a|=﹣a,=﹣1,|c|=c,化简|a+b|﹣|a﹣c|﹣|b﹣c|= ﹣2c .
【分析】根据题意,利用绝对值的代数意义判断出a,b,c的正负,原式利用绝对值的代数意义化简即可得到结果.
【解答】解:∵|a|=﹣a,=﹣1,|c|=c,
∴a为非正数,b为负数,c为非负数,
∴a+b≤0,a﹣c≤0,b﹣c≤0,
则原式=﹣a﹣b+a﹣c+b﹣c=﹣2c,
故答案为:﹣2c
【点评】此题考查了有理数的减法,以及绝对值,熟练掌握绝对值的代数意义是解本题的关键.
12.(4分)在数A的右端再加上一个数字6,则该数比原数增加2004,那么A= 222 .
【分析】本题题意比较抽象,关键是根据题意判定数A是三位数,会设这个三位数,根据题意列方程,用整体观点解题.
【解答】解:在数A的右端再加上一个数字6,则该数比原数增加2004,可知这个数至少是一个三位数,
设这个数为100x+10y+z,在数A的右端再加上一个数字6之后,就变成了1000x+100y+10z+6,依题意列方程,得
1000x+100y+10z+6﹣(100x+10y+z)=2004,
整理得1:00x+10y+z=222.
【点评】本题主要考查了三位数的含义,注意做这道题时要把100x+10y+z当成一个整体.
13.(4分)若x2=9,|y|=4且x<y,则x+y= 7或1 .
【分析】根据绝对值和偶次方求出x、y,再根据x<y求出x、y,最后代入求出即可.
【解答】解:∵x2=9,|y|=4,
∴x=±3,y=±4,
∵x<y,
∴x=3,y=4或x=﹣3,y=4,
∴当x=3,y=4时,x+y=7;
当x=﹣3,y=4时,x+y=1,
故答案为:7或1.
【点评】本题考查了绝对值、偶次方、有理数的加法等知识点,能求出符合的所有情况是解此题的关键.
14.(4分)若|a|=8,|b|=3,则当a与b异号时,a+b= ﹣5或5 .
【分析】先根据绝对值和已知求出a、b的值,再代入求出即可.
【解答】解:∵|a|=8,|b|=3,
∴a=±8,b=±3,
∵a与b异号,
∴a=8,b=﹣3或a=﹣8,b=3,
当a=8,b=﹣3时,a+b=5,
当a=﹣8,b=3时,a+b=﹣5,
故答案为:﹣5或5.
【点评】本题考查了绝对值和有理数的加法,能求出符合的所有情况是解此题的关键.
15.(4分)若|a|=6,|b|=2,且|a+b|=a+b,则a﹣b的值 4或8 .
【分析】根据绝对值的意义,已知|a|=4,|b|=2,可以确定a,b的值,根据|a+b|=a+b知a=6,b=2或b=﹣2,再分别求解可得.
【解答】解:∵|a|=6,|b|=2,
∴a=±6,b=±2,
∵|a+b|=a+b,
∴a+b≥0,
则a=6,b=2或b=﹣2,
∴当a=6,b=2时,a﹣b=6﹣2=4;
当a=6,b=﹣2时,a﹣b=6﹣(﹣2)=8;
综上,a﹣b的值为4或8,
故答案为:4或8.
【点评】本题主要考查有理数的减法,根据绝对值的意义,准确确定a、b的值是解题的关键.
三、解答题(
本大题共5小题,共40.0分)
16.(8分)观察下面的等式:
﹣1=﹣|﹣+2|+3;
3﹣1=﹣|﹣1+2|+3;
1﹣1=﹣|1+2|+3;
(﹣)﹣1=﹣|+2|+3;
(﹣2)﹣1=﹣|4+2|+3
回答下列问题:
(1)填空: ﹣3 ﹣1=﹣|5+2|+3;
(2)已知2﹣1=﹣|x+2|+3,则x的值是 0 ;
(3)设满足上面特征的等式最左边的数为y,求y的最大值,并写出此时的等式.
【分析】(1)根据a﹣1=﹣|2﹣a+2|+3即可求解;
(2)由(1)的规律即可求解;
(3)由(1)可得|4﹣a|=4﹣a,根据非负数的性质即可求解.
【解答】解:观察可知:a﹣1=﹣|2﹣a+2|+3,
则(1)﹣3﹣1=﹣|5+2|+3;
(2)已知2﹣1=﹣|x+2|+3,则x的值是0;
(3)由a﹣1=﹣|2﹣a+2|+3,可得|4﹣a|=4﹣a,
则4﹣a≥0,解得a≤4,
即y的最大值是4,
此时的等式是4﹣1=﹣|﹣2+2|+3.
故答案为:﹣3;0.
【点评】考查了有理数的减法,非负数的性质,关键是得到算式的特征是a﹣1=﹣|2﹣a+2|+3.
17.(8分)在解决数学问题的过程中,我们常用到“分类讨论”的数学思想,下面是运用分类讨论的数学思想解决问题的过程,请仔细阅读,并解答题目后提出的【探究】.
【提出问题】两个有理数a、b满足a、b同号,求+的值.
【解决问题】
解:由a、b同号,可知a、b有两种可能:①当a,b都正数;②当a,b都是负数.①若a、b都是正数,即a>0,b>0,有|a|=a,|b|=b,则+=+=1+1=2;②若a、b都是负数,即a<0,b<0,有|a|=﹣a,|b|=﹣b,则+=+=(﹣1)+(﹣1)=﹣2,所以+的值为2或﹣2.
【探究】请根据上面的解题思路解答下面的问题:
(1)两个有理数a、b满足a、b异号,求+的值;
(2)已知|a|=3,|b|=7,且a<b,求a+b的值.
【分析】(1)直接利用①当a>0,b<0;②当b>0,a<0,进而得出答案;
(2)利用绝对值的性质分类讨论得出答案.
【解答】解:(1)∵两个有理数a、b满足a、b异号,
∴有两种可能,①a是正数,b是负数;②b是正数,a是负数;
①当a>0,b<0,则+=1﹣1=0;
②当b>0,a<0,则+=﹣1+1=0;
综上,+的值为0;
(2)∵|a|=3,|b|=7,且a<b,
∴a=3或﹣3,b=7或﹣7
①当a=﹣3,则b=7,此时a+b=4;
②当a=3,则b=7,此时a+b=10;
综上可得:a+b的值为4或10.
【点评】此题主要考查了绝对值,正确分类讨论是解题关键.
18.(8分)在一个3×3的方格中填写了9个数字,使得每行、每列、每条对角线上的三个数之和相等,得到的3×3的方格称为一个三阶幻方.
(1)在图1中空格处填上合适的数字,使它构成一个三阶幻方;
(2)如图2的方格中填写了一些数和字母,当x+y的值为多少时,它能构成一个三阶幻方.
【分析】(1)根据三个数的和为2+3+4=9,依次列式计算即可求解;
(2)先求出下面中间的数,进一步得到右上面的数,从而得到x、y的值,相加可求x+y的值.
【解答】解:(1)2+3+4=9,
9﹣6﹣4=﹣1,
9﹣6﹣2=1,
9﹣2﹣7=0,
9﹣4﹣0=5,
如图所示:
(2)﹣3+1﹣4=﹣6,
﹣6+1﹣(﹣3)=﹣2,
﹣2+1+4=3,
如图所示:
x=3﹣4﹣(﹣6)=5,
y=3﹣1﹣(﹣6)=8,
x+y=5+8=13.
【点评】本题考查了有理数的加法,根据表格,先求出三个数的和是解题的关键,也是本题的突破口.
19.(8分)已知a是最小的正整数,b是最大的负整数,c是绝对值最小的有理数,表示有理数d的点到原点的距离为4,求a﹣b﹣c+d的值.
【分析】根据最小的正整数为1,最大的负整数为﹣1,绝对值最小的有理数为0,以及点到原点的距离的定义,确定出a,b,c,d的值,即可求出a﹣b﹣c+d即可求出值.
【解答】解:∵a是最小的正整数,b是最大的负整数,c是绝对值最小的有理数,表示有理数d的点到原点的距离为4,
∴a=1,b=﹣1,c=0,d=±4,
则当a=1,b=﹣1,c=0,d=﹣4时,a﹣b﹣c+d=1+1﹣0﹣4=﹣2;
当a=1,b=﹣1,c=0,d=4时,a﹣b﹣c+d=1+1﹣0+4=6.
故a﹣b﹣c+d的值为﹣2或6.
【点评】此题考查了有理数的加减混合运算,有理数,绝对值,以及数轴,熟练掌握各自的定义是解本题的关键.
20.(8分)阅读下面文字:
对于(﹣5)+(﹣9)+17+(﹣3)
可以如下计算:
原式=[(﹣5)+(﹣)]+[(﹣9)+(﹣)]+(17+)+[(﹣3)+(﹣)]
=[(﹣5)+(﹣9)+17+(﹣3)]+[(﹣)+(﹣)++(﹣)]
=0+(﹣1)
=﹣1
上面这种方法叫折项法,你看懂了吗?
仿照上面的方法,计算:(1)﹣1+(﹣2)+7+(﹣4)=
计算:(2)(﹣2017)+2016+(﹣2015)+16.
【分析】(1)仿照题示解题过程,将整数部分相加减、分数部分相加减,再计算可得;
(2)仿照题示解题过程,将整数部分相加减、分数部分相加减,再计算可得
【解答】解:(1)原式=(﹣1﹣2+7﹣4)+(﹣﹣+﹣)=﹣,
故答案为:﹣;
(2)原式=(﹣2017+2016﹣2015+16)+(﹣+﹣+)
=﹣2000﹣
=﹣2000
【点评】本题主要考查有理数的加减混合运算,解题的关键是熟练掌握有理数的混合运算法则和运算律.
第17页(共17页)
一、选择题(
本大题共10小题,共40.0分)
1.(4分)设a为最小的正整数,b为最大的负整数,c是绝对值最小的有理数,则a+b﹣c的值为( )
A.0
B.2
C.﹣2
D.2或﹣2
2.(4分)若a<0,b>0,且|a|<|b|,则a+b的值一定是( )
A.正数
B.负数
C.0
D.非负数
3.(4分)若|x|=3,|y|=4,则|x+y|的值为( )
A.7
B.﹣7
C.7或1
D.以上都不对
4.(4分)如果a+b+c=0,且|c|>|b|>|a|,则下列说法中可能成立的是( )
A.a、b为正数,c为负数
B.a、c为正数,b为负数
C.b、c为正数,a为负数
D.a、c为正数,b为负数
5.(4分)计算1﹣3+5﹣7+9=(1+5+9)+(﹣3﹣7)是应用了( )
A.加法交换律
B.加法结合律
C.分配律
D.加法交换律与结合律
6.(4分)|a|+|b|=|a+b|,则a,b关系是( )
A.a,b的绝对值相等
B.a,b异号
C.a+b的和是非负数
D.a、b同号或a、b其中一个为0
7.(4分)如表为蒙城县2018年某日天气预报信息,根据图表可知当天最高气温比最低气温高了( )
2018年1月6日蒙城天气预报
天气现象
气温
1月6日
星期六
白天
晴
高温7℃
夜间
晴
低温﹣5℃
A.2℃
B.﹣2℃
C.12℃
D.﹣12℃
8.(4分)已知x=1,|y|=2且x>y,则x﹣y的值是( )
A.﹣1
B.﹣3
C.1
D.3
9.(4分)如图表格是一个4×4的奇妙方阵;
从这个方阵中选四个数(其中任何两个既不在同一行,也不在同一列),虽然有很多种选法,但每次选出的四个数相加,其和是一个定值.则方阵中空白处的数是( )
A.5
B.6
C.7
D.8
10.(4分)如图,从左到右在每个小格子中填入一个整数,使得其中任意三个相邻格子中所填整数之和都相等.若前m个格子中所填整数之和是1684,则m的值可以是( )
A.1015
B.1010
C.1012
D.1018
二、填空题(
本大题共5小题,共20.0分)
11.(4分)已知,|a|=﹣a,=﹣1,|c|=c,化简|a+b|﹣|a﹣c|﹣|b﹣c|=
.
12.(4分)在数A的右端再加上一个数字6,则该数比原数增加2004,那么A=
.
13.(4分)若x2=9,|y|=4且x<y,则x+y=
.
14.(4分)若|a|=8,|b|=3,则当a与b异号时,a+b=
.
15.(4分)若|a|=6,|b|=2,且|a+b|=a+b,则a﹣b的值
.
三、解答题(
本大题共5小题,共40.0分)
16.(8分)观察下面的等式:
﹣1=﹣|﹣+2|+3;
3﹣1=﹣|﹣1+2|+3;
1﹣1=﹣|1+2|+3;
(﹣)﹣1=﹣|+2|+3;
(﹣2)﹣1=﹣|4+2|+3
回答下列问题:
(1)填空:
﹣1=﹣|5+2|+3;
(2)已知2﹣1=﹣|x+2|+3,则x的值是
;
(3)设满足上面特征的等式最左边的数为y,求y的最大值,并写出此时的等式.
17.(8分)在解决数学问题的过程中,我们常用到“分类讨论”的数学思想,下面是运用分类讨论的数学思想解决问题的过程,请仔细阅读,并解答题目后提出的【探究】.
【提出问题】两个有理数a、b满足a、b同号,求+的值.
【解决问题】
解:由a、b同号,可知a、b有两种可能:①当a,b都正数;②当a,b都是负数.①若a、b都是正数,即a>0,b>0,有|a|=a,|b|=b,则+=+=1+1=2;②若a、b都是负数,即a<0,b<0,有|a|=﹣a,|b|=﹣b,则+=+=(﹣1)+(﹣1)=﹣2,所以+的值为2或﹣2.
【探究】请根据上面的解题思路解答下面的问题:
(1)两个有理数a、b满足a、b异号,求+的值;
(2)已知|a|=3,|b|=7,且a<b,求a+b的值.
18.(8分)在一个3×3的方格中填写了9个数字,使得每行、每列、每条对角线上的三个数之和相等,得到的3×3的方格称为一个三阶幻方.
(1)在图1中空格处填上合适的数字,使它构成一个三阶幻方;
(2)如图2的方格中填写了一些数和字母,当x+y的值为多少时,它能构成一个三阶幻方.
19.(8分)已知a是最小的正整数,b是最大的负整数,c是绝对值最小的有理数,表示有理数d的点到原点的距离为4,求a﹣b﹣c+d的值.
20.(8分)阅读下面文字:
对于(﹣5)+(﹣9)+17+(﹣3)
可以如下计算:
原式=[(﹣5)+(﹣)]+[(﹣9)+(﹣)]+(17+)+[(﹣3)+(﹣)]
=[(﹣5)+(﹣9)+17+(﹣3)]+[(﹣)+(﹣)++(﹣)]
=0+(﹣1)
=﹣1
上面这种方法叫折项法,你看懂了吗?
仿照上面的方法,计算:(1)﹣1+(﹣2)+7+(﹣4)=
计算:(2)(﹣2017)+2016+(﹣2015)+16.
参考答案与试题解析
一、选择题(
本大题共10小题,共40.0分)
1.(4分)设a为最小的正整数,b为最大的负整数,c是绝对值最小的有理数,则a+b﹣c的值为( )
A.0
B.2
C.﹣2
D.2或﹣2
【分析】由a为最小的正整数,b为最大的负整数,c是绝对值最小的有理数,可分别得出a、b、c的值,代入计算可得结果.
【解答】解:根据题意知a=1,b=﹣1,c=0,
则a+b﹣c=1﹣1+0=0,
故选:A.
【点评】本题主要考查有理数的概念的理解,能正确判断有关有理数的概念是解题的关键.
2.(4分)若a<0,b>0,且|a|<|b|,则a+b的值一定是( )
A.正数
B.负数
C.0
D.非负数
【分析】根据题意,利用绝对值的代数意义,以及有理数的加法法则判断即可.
【解答】解:∵a<0,b>0,且|a|<|b|,
∴a+b的值一定是正数,
故选:A.
【点评】本题主要考查有理数的加法,在进行有理数加法运算时,首先判断两个加数的符号:是同号还是异号,是否有0.从而确定用那一条法则.在应用过程中,要牢记“先符号,后绝对值”.
3.(4分)若|x|=3,|y|=4,则|x+y|的值为( )
A.7
B.﹣7
C.7或1
D.以上都不对
【分析】根据绝对值的性质进行分类讨论计算即可.
【解答】解:由|x|=3,|y|=4
可得
x=±3,y=±4,
所以|x+y|=|3+4|=7,或|x+y|=|﹣3﹣4|=7,或|x+y|=|3﹣4|=1,或|x+y|=|﹣3+4|=1
综上所述|x+y|的值为7或1.
故选:C.
【点评】此题主要考查与绝对值有关的计算,根据绝对值的性质合理全面的进行分类是解题的关键.
4.(4分)如果a+b+c=0,且|c|>|b|>|a|,则下列说法中可能成立的是( )
A.a、b为正数,c为负数
B.a、c为正数,b为负数
C.b、c为正数,a为负数
D.a、c为正数,b为负数
【分析】根据有理数的加法,一对相反数的和为0,可得a、b、c中至少有一个为正数,至少有一个为负数,又|c|>|b|>|a|,那么|c|=|b|+|a|,进而得出可能存在的情况.
【解答】解:∵a+b+c=0,
∴a、b、c中至少有一个为正数,至少有一个为负数,
∵|c|>|b|>|a|,
∴|c|=|b|+|a|,
∴可能a、b为正数,c为负数;也可能a、b为负数,c为正数.
故选:A.
【点评】本题主要考查的是有理数的加法,绝对值的意义,掌握有理数的加法法则是解题的关键.
5.(4分)计算1﹣3+5﹣7+9=(1+5+9)+(﹣3﹣7)是应用了( )
A.加法交换律
B.加法结合律
C.分配律
D.加法交换律与结合律
【分析】根据加法交换律与结合律即可求解.
【解答】解:计算1﹣3+5﹣7+9=(1+5+9)+(﹣3﹣7)是应用了加法交换律与结合律.
故选:D.
【点评】考查了有理数的加减混合运算,方法指引:①在一个式子里,有加法也有减法,根据有理数减法法则,把减法都转化成加法,并写成省略括号的和的形式.
②转化成省略括号的代数和的形式,就可以应用加法的运算律,使计算简化.
6.(4分)|a|+|b|=|a+b|,则a,b关系是( )
A.a,b的绝对值相等
B.a,b异号
C.a+b的和是非负数
D.a、b同号或a、b其中一个为0
【分析】每一种情况都举出例子,再判断即可.
【解答】解:A、当a、b的绝对值相等时,如a=1,b=﹣1,|a|+|b|=2,|a+b|=0,即|a|+|b|≠|a+b|,故本选项不符合题意;
B、当a、b异号时,如a=1,b=﹣3,|a|+|b|=4,|a+b|=2,即|a|+|b|≠|a+b|,故本选项不符合题意;
C、当a+b的和是非负数时,如:a=﹣1,b=3,|a|+|b|=4,|a+b|=2,即即|a|+|b|≠|a+b|,故本选项不符合题意;
D、当a、b同号或a、b其中一个为0时,|a|+|b|=|a+b|,故本选项符合题意;
故选:D.
【点评】本题考查了绝对值、有理数的加法等知识点,能根据选项举出反例是解此题的关键.
7.(4分)如表为蒙城县2018年某日天气预报信息,根据图表可知当天最高气温比最低气温高了( )
2018年1月6日蒙城天气预报
天气现象
气温
1月6日
星期六
白天
晴
高温7℃
夜间
晴
低温﹣5℃
A.2℃
B.﹣2℃
C.12℃
D.﹣12℃
【分析】用最高气温减去最低气温,列出算式计算即可求解.
【解答】解:7﹣(﹣5)=12(℃).
故选:C.
【点评】此题主要考查了有理数的减法,关键是掌握有理数减法法则:减去一个数,等于加上这个数的相反数.
8.(4分)已知x=1,|y|=2且x>y,则x﹣y的值是( )
A.﹣1
B.﹣3
C.1
D.3
【分析】根据题意,利用绝对值的代数意义求出y的值,即可求出x﹣y的值.
【解答】解:∵x=1,|y|=2且x>y,
∴x=1,y=﹣2,
则x﹣y=3.
故选:D.
【点评】此题考查了代数式求值,绝对值,熟练掌握运算法则是解本题的关键.
9.(4分)如图表格是一个4×4的奇妙方阵;
从这个方阵中选四个数(其中任何两个既不在同一行,也不在同一列),虽然有很多种选法,但每次选出的四个数相加,其和是一个定值.则方阵中空白处的数是( )
A.5
B.6
C.7
D.8
【分析】设空白处的数为x,根据“每次选出的四个数相加,其和是一个定值”可得1﹣2+x+6=4﹣1+6+3,解之即可.
【解答】解:设空白处的数为x,
则1﹣2+x+6=4﹣1+6+3,
解得:x=7,
故选:C.
【点评】本题主要考查一元一次方程,解题的关键是理解题意列出关于空白处数字的方程.
10.(4分)如图,从左到右在每个小格子中填入一个整数,使得其中任意三个相邻格子中所填整数之和都相等.若前m个格子中所填整数之和是1684,则m的值可以是( )
A.1015
B.1010
C.1012
D.1018
【分析】根据题意可求得c=9,然后求得9+(﹣5)+1=5,然后按照规律可求得m的值.
【解答】解:由题意可知:9+a+b=a+b+c,
∴c=9.
∵9﹣5+1=5,
1684÷5=336…4,
且9﹣5=4,
∴m=336×3+2=1010.
故选:B.
【点评】此题考查数字的变化规律,找出数字之间的联系得出规律是解决问题的关键.
二、填空题(
本大题共5小题,共20.0分)
11.(4分)已知,|a|=﹣a,=﹣1,|c|=c,化简|a+b|﹣|a﹣c|﹣|b﹣c|= ﹣2c .
【分析】根据题意,利用绝对值的代数意义判断出a,b,c的正负,原式利用绝对值的代数意义化简即可得到结果.
【解答】解:∵|a|=﹣a,=﹣1,|c|=c,
∴a为非正数,b为负数,c为非负数,
∴a+b≤0,a﹣c≤0,b﹣c≤0,
则原式=﹣a﹣b+a﹣c+b﹣c=﹣2c,
故答案为:﹣2c
【点评】此题考查了有理数的减法,以及绝对值,熟练掌握绝对值的代数意义是解本题的关键.
12.(4分)在数A的右端再加上一个数字6,则该数比原数增加2004,那么A= 222 .
【分析】本题题意比较抽象,关键是根据题意判定数A是三位数,会设这个三位数,根据题意列方程,用整体观点解题.
【解答】解:在数A的右端再加上一个数字6,则该数比原数增加2004,可知这个数至少是一个三位数,
设这个数为100x+10y+z,在数A的右端再加上一个数字6之后,就变成了1000x+100y+10z+6,依题意列方程,得
1000x+100y+10z+6﹣(100x+10y+z)=2004,
整理得1:00x+10y+z=222.
【点评】本题主要考查了三位数的含义,注意做这道题时要把100x+10y+z当成一个整体.
13.(4分)若x2=9,|y|=4且x<y,则x+y= 7或1 .
【分析】根据绝对值和偶次方求出x、y,再根据x<y求出x、y,最后代入求出即可.
【解答】解:∵x2=9,|y|=4,
∴x=±3,y=±4,
∵x<y,
∴x=3,y=4或x=﹣3,y=4,
∴当x=3,y=4时,x+y=7;
当x=﹣3,y=4时,x+y=1,
故答案为:7或1.
【点评】本题考查了绝对值、偶次方、有理数的加法等知识点,能求出符合的所有情况是解此题的关键.
14.(4分)若|a|=8,|b|=3,则当a与b异号时,a+b= ﹣5或5 .
【分析】先根据绝对值和已知求出a、b的值,再代入求出即可.
【解答】解:∵|a|=8,|b|=3,
∴a=±8,b=±3,
∵a与b异号,
∴a=8,b=﹣3或a=﹣8,b=3,
当a=8,b=﹣3时,a+b=5,
当a=﹣8,b=3时,a+b=﹣5,
故答案为:﹣5或5.
【点评】本题考查了绝对值和有理数的加法,能求出符合的所有情况是解此题的关键.
15.(4分)若|a|=6,|b|=2,且|a+b|=a+b,则a﹣b的值 4或8 .
【分析】根据绝对值的意义,已知|a|=4,|b|=2,可以确定a,b的值,根据|a+b|=a+b知a=6,b=2或b=﹣2,再分别求解可得.
【解答】解:∵|a|=6,|b|=2,
∴a=±6,b=±2,
∵|a+b|=a+b,
∴a+b≥0,
则a=6,b=2或b=﹣2,
∴当a=6,b=2时,a﹣b=6﹣2=4;
当a=6,b=﹣2时,a﹣b=6﹣(﹣2)=8;
综上,a﹣b的值为4或8,
故答案为:4或8.
【点评】本题主要考查有理数的减法,根据绝对值的意义,准确确定a、b的值是解题的关键.
三、解答题(
本大题共5小题,共40.0分)
16.(8分)观察下面的等式:
﹣1=﹣|﹣+2|+3;
3﹣1=﹣|﹣1+2|+3;
1﹣1=﹣|1+2|+3;
(﹣)﹣1=﹣|+2|+3;
(﹣2)﹣1=﹣|4+2|+3
回答下列问题:
(1)填空: ﹣3 ﹣1=﹣|5+2|+3;
(2)已知2﹣1=﹣|x+2|+3,则x的值是 0 ;
(3)设满足上面特征的等式最左边的数为y,求y的最大值,并写出此时的等式.
【分析】(1)根据a﹣1=﹣|2﹣a+2|+3即可求解;
(2)由(1)的规律即可求解;
(3)由(1)可得|4﹣a|=4﹣a,根据非负数的性质即可求解.
【解答】解:观察可知:a﹣1=﹣|2﹣a+2|+3,
则(1)﹣3﹣1=﹣|5+2|+3;
(2)已知2﹣1=﹣|x+2|+3,则x的值是0;
(3)由a﹣1=﹣|2﹣a+2|+3,可得|4﹣a|=4﹣a,
则4﹣a≥0,解得a≤4,
即y的最大值是4,
此时的等式是4﹣1=﹣|﹣2+2|+3.
故答案为:﹣3;0.
【点评】考查了有理数的减法,非负数的性质,关键是得到算式的特征是a﹣1=﹣|2﹣a+2|+3.
17.(8分)在解决数学问题的过程中,我们常用到“分类讨论”的数学思想,下面是运用分类讨论的数学思想解决问题的过程,请仔细阅读,并解答题目后提出的【探究】.
【提出问题】两个有理数a、b满足a、b同号,求+的值.
【解决问题】
解:由a、b同号,可知a、b有两种可能:①当a,b都正数;②当a,b都是负数.①若a、b都是正数,即a>0,b>0,有|a|=a,|b|=b,则+=+=1+1=2;②若a、b都是负数,即a<0,b<0,有|a|=﹣a,|b|=﹣b,则+=+=(﹣1)+(﹣1)=﹣2,所以+的值为2或﹣2.
【探究】请根据上面的解题思路解答下面的问题:
(1)两个有理数a、b满足a、b异号,求+的值;
(2)已知|a|=3,|b|=7,且a<b,求a+b的值.
【分析】(1)直接利用①当a>0,b<0;②当b>0,a<0,进而得出答案;
(2)利用绝对值的性质分类讨论得出答案.
【解答】解:(1)∵两个有理数a、b满足a、b异号,
∴有两种可能,①a是正数,b是负数;②b是正数,a是负数;
①当a>0,b<0,则+=1﹣1=0;
②当b>0,a<0,则+=﹣1+1=0;
综上,+的值为0;
(2)∵|a|=3,|b|=7,且a<b,
∴a=3或﹣3,b=7或﹣7
①当a=﹣3,则b=7,此时a+b=4;
②当a=3,则b=7,此时a+b=10;
综上可得:a+b的值为4或10.
【点评】此题主要考查了绝对值,正确分类讨论是解题关键.
18.(8分)在一个3×3的方格中填写了9个数字,使得每行、每列、每条对角线上的三个数之和相等,得到的3×3的方格称为一个三阶幻方.
(1)在图1中空格处填上合适的数字,使它构成一个三阶幻方;
(2)如图2的方格中填写了一些数和字母,当x+y的值为多少时,它能构成一个三阶幻方.
【分析】(1)根据三个数的和为2+3+4=9,依次列式计算即可求解;
(2)先求出下面中间的数,进一步得到右上面的数,从而得到x、y的值,相加可求x+y的值.
【解答】解:(1)2+3+4=9,
9﹣6﹣4=﹣1,
9﹣6﹣2=1,
9﹣2﹣7=0,
9﹣4﹣0=5,
如图所示:
(2)﹣3+1﹣4=﹣6,
﹣6+1﹣(﹣3)=﹣2,
﹣2+1+4=3,
如图所示:
x=3﹣4﹣(﹣6)=5,
y=3﹣1﹣(﹣6)=8,
x+y=5+8=13.
【点评】本题考查了有理数的加法,根据表格,先求出三个数的和是解题的关键,也是本题的突破口.
19.(8分)已知a是最小的正整数,b是最大的负整数,c是绝对值最小的有理数,表示有理数d的点到原点的距离为4,求a﹣b﹣c+d的值.
【分析】根据最小的正整数为1,最大的负整数为﹣1,绝对值最小的有理数为0,以及点到原点的距离的定义,确定出a,b,c,d的值,即可求出a﹣b﹣c+d即可求出值.
【解答】解:∵a是最小的正整数,b是最大的负整数,c是绝对值最小的有理数,表示有理数d的点到原点的距离为4,
∴a=1,b=﹣1,c=0,d=±4,
则当a=1,b=﹣1,c=0,d=﹣4时,a﹣b﹣c+d=1+1﹣0﹣4=﹣2;
当a=1,b=﹣1,c=0,d=4时,a﹣b﹣c+d=1+1﹣0+4=6.
故a﹣b﹣c+d的值为﹣2或6.
【点评】此题考查了有理数的加减混合运算,有理数,绝对值,以及数轴,熟练掌握各自的定义是解本题的关键.
20.(8分)阅读下面文字:
对于(﹣5)+(﹣9)+17+(﹣3)
可以如下计算:
原式=[(﹣5)+(﹣)]+[(﹣9)+(﹣)]+(17+)+[(﹣3)+(﹣)]
=[(﹣5)+(﹣9)+17+(﹣3)]+[(﹣)+(﹣)++(﹣)]
=0+(﹣1)
=﹣1
上面这种方法叫折项法,你看懂了吗?
仿照上面的方法,计算:(1)﹣1+(﹣2)+7+(﹣4)=
计算:(2)(﹣2017)+2016+(﹣2015)+16.
【分析】(1)仿照题示解题过程,将整数部分相加减、分数部分相加减,再计算可得;
(2)仿照题示解题过程,将整数部分相加减、分数部分相加减,再计算可得
【解答】解:(1)原式=(﹣1﹣2+7﹣4)+(﹣﹣+﹣)=﹣,
故答案为:﹣;
(2)原式=(﹣2017+2016﹣2015+16)+(﹣+﹣+)
=﹣2000﹣
=﹣2000
【点评】本题主要考查有理数的加减混合运算,解题的关键是熟练掌握有理数的混合运算法则和运算律.
第17页(共17页)
同课章节目录
