2021-2022学年湘教版七年级上数学1.6有理数的乘方 同步练习(word解析版)
文档属性
| 名称 | 2021-2022学年湘教版七年级上数学1.6有理数的乘方 同步练习(word解析版) |

|
|
| 格式 | docx | ||
| 文件大小 | 50.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-19 00:00:00 | ||
图片预览




文档简介
《1.6有理数的乘方》同步练习
一、选择题(
本大题共10小题,共40.0分)
1.(4分)若(b+1)2+3|a﹣2|=0,则a﹣2b的值是( )
A.﹣4
B.0
C.4
D.2
2.(4分)关于﹣(﹣a)2的相反数,有下列说法:①等于a2;②等于(﹣a)2;③值可能为0;④值一定是正数.其中正确的有( )
A.1个
B.2个
C.3个
D.4个
3.(4分)下列结论中,错误的个数为( )
﹣(﹣2)2=4;﹣5÷=﹣5;;=﹣3;﹣33=﹣9.
A.2个
B.3个
C.4个
D.5个
4.(4分)若a、b有理数,下列判断:
①a2+(b+1)2总是正数;
②a2+b2+1总是正数;
③9+(a﹣b)2的最小值为9;
④1﹣(ab+1)2的最大值是0
其中错误的个数是( )
A.1
B.2
C.3
D.4
5.(4分)当a<0时,下列式子成立的个数是( )
①|a|=a;②a2>0;③a3<0;④a2=(﹣a)2;⑤a3=﹣a3
A.1个
B.2个
C.3个
D.4个
6.(4分)已知x,y满足|x﹣3|+(y+4)2=0,则代数式(x+y)2018的值为( )
A.﹣1
B.1
C.2018
D.﹣2018
7.(4分)若|m﹣1|+n2+6n+9=0,那么m、n的值分别为( )
A.m=1,n=﹣3
B.m=﹣1,n=﹣3
C.m=﹣1,n=3
D.m=1,n=3
8.(4分)据慈利红网消息,今年“十一”假期,慈利县各景点共接待游客29.15万人次,将29.15万用科学记数法表示为( )
A.29.15×104
B.2.915×104
C.2.915×105
D.2.915×106
9.(4分)用百度搜索关键词“十九大”,百度为我们找到相关结果约18
600
000个,把18
600
000这个数用科学记数法表示为( )
A.0.186×108
B.1.86×107
C.18.6×106
D.186×105
10.(4分)据相关报道,开展精准扶贫户工作五年来,我国约有5500万人摆脱贫困,国家发放扶贫资金共375亿元.将375亿用科学记数法表示为( )
A.375×107
B.3.75×1010
C.3.75×109
D.37.5×108
二、填空题(
本大题共5小题,共20.0分)
11.(4分)若|a+1|+(b﹣2)2=0,则(a+b)3+a5的值为
.
12.(4分)《九章算术》是中国古代第一部数学专著,不仅最早提到分数问题,也首先记录了盈不足等问题,在第七章“盈不足”中有这样一个问题:“今有蒲生一日,长三尺;莞生一日,长一尺.蒲生日自半,莞生日自倍.问几何日而长等?”其意思是“有蒲和莞两种植物,蒲第一日长了3尺,莞第一日长了1尺,以后蒲每日生长的长度是前一日的一半,莞每日生长的长度是前一日的2倍,问几日蒲、莞上涨的长度相等.”
请计算出第三日后,蒲、莞的长度相差为
尺.
13.(4分)南海海域面积约为3500000平方千米,该面积用科学记数法应表示为
平方千米.
14.(4分)40.02万精确到
位,1.2349×105按四舍五入精确到千位得到的近似数为
.
15.(4分)一种电子计算机每秒可以进行3×108次运算,它工作2×102秒可进行
次运算.
三、解答题(
本大题共5小题,共40.0分)
16.(8分)阅读下列各式:(a×b)2=a2×b2,(a×b)3=a3×b3,(a×b)4=a4×b4(a×b)5=a5×b5……回答下列三个问题:
(1)猜想:(a×b)n=
.
(2)请用我们学过的知识说明上式成立的理由.
(3)请计算:(﹣0.125)2019×22018×42017
17.(8分)若有理数a、b、c满足:(a﹣1)2+(2a﹣b)4+|3c+1|=0.求(c﹣a)2+c3﹣b的值.
18.(8分)我们常用的数是十进制数,如4657=4×103+6×102+5×101+7×100,数要用10个数码(又叫数字):0、1、2、3、4、5、6、7、8、9,在电子计算机中用的二进制,只要两个数码:0和1,如二进制中110=1×22+1×21+0×20等于十进制的数6,110101=1×25+1×24+0×23+1×22+0×21+1×20等于十进制的数53.那么二进制中的数101011等于十进制中的哪个数?
19.(8分)小明爸爸给小明出了一道题,说明他本月炒股的盈亏情况(单位:元)
股票
每股净赚(元)
股票
招商银行
+23
500
浙江医药
﹣(﹣2.8)
1000
晨光文具
﹣1.5
1500
金龙汽车
﹣1
2000
请你也来计算一下,小明爸爸本月投资炒股到底是赔了还是赚了?赔了或赚了多少元?
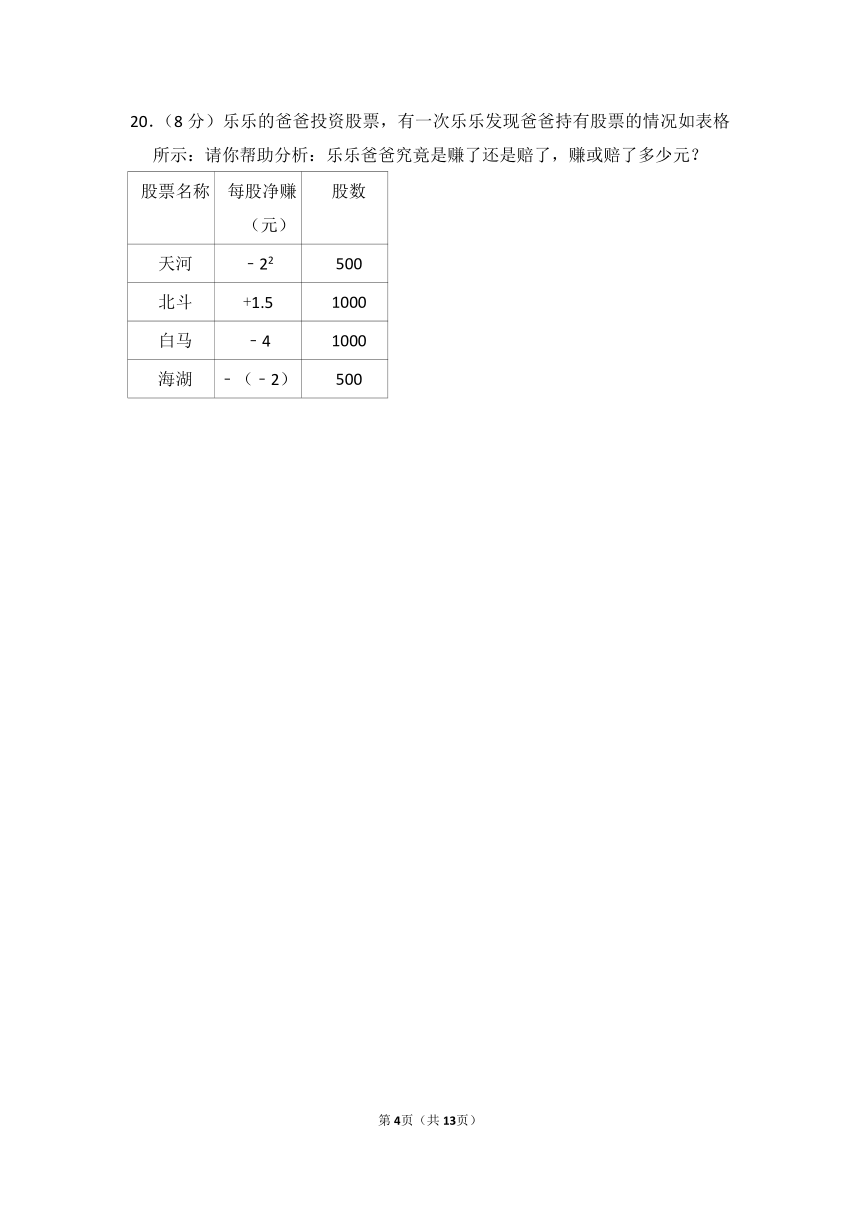
20.(8分)乐乐的爸爸投资股票,有一次乐乐发现爸爸持有股票的情况如表格所示:请你帮助分析:乐乐爸爸究竟是赚了还是赔了,赚或赔了多少元?
股票名称
每股净赚(元)
股数
天河
﹣22
500
北斗
+1.5
1000
白马
﹣4
1000
海湖
﹣(﹣2)
500
参考答案与试题解析
一、选择题(
本大题共10小题,共40.0分)
1.(4分)若(b+1)2+3|a﹣2|=0,则a﹣2b的值是( )
A.﹣4
B.0
C.4
D.2
【分析】首先根据非负数的性质可求出a、b的值,进而可求出a﹣2b的值.
【解答】解:∵(b+1)2+3|a﹣2|=0,
∴a﹣2=0,b+1=0,
解得a=2,b=﹣1;
∴a﹣2b=2﹣(﹣2)=4.
故选:C.
【点评】此题主要考查了非负数的性质,初中阶段有三种类型的非负数:绝对值、偶次方、二次根式(算术平方根).当它们相加和为0时,必须满足其中的每一项都等于0.
2.(4分)关于﹣(﹣a)2的相反数,有下列说法:①等于a2;②等于(﹣a)2;③值可能为0;④值一定是正数.其中正确的有( )
A.1个
B.2个
C.3个
D.4个
【解答】解:①∵﹣(﹣a)2=﹣a2,∴它的相反数是a2.显然是正确的.
②∵(﹣a)2=a2,∴也是正确的.
③当a=0时,a2=0,∴原式的值可能为0,也是正确的.
④是错误的,没有考虑0.
故有3个是正确的.
故选:C.
【点评】注意0既不是正数也不是负数,0的相反数是0.
3.(4分)下列结论中,错误的个数为( )
﹣(﹣2)2=4;﹣5÷=﹣5;;=﹣3;﹣33=﹣9.
A.2个
B.3个
C.4个
D.5个
【分析】根据有理数的乘方法则,乘法法则一一计算即可即可判断;
【解答】解:﹣(﹣2)2=4;错误,应该是﹣4;
﹣5÷=﹣5;错误,应该是﹣25;
;错误,应该是;
=﹣3;正确;
﹣33=﹣9.错误,应该是﹣27.
故选:C.
【点评】本题考查有理数的乘方,解题的关键是熟练掌握有理数的乘法法则,乘法法则,属于中考常考题型.
4.(4分)若a、b有理数,下列判断:
①a2+(b+1)2总是正数;
②a2+b2+1总是正数;
③9+(a﹣b)2的最小值为9;
④1﹣(ab+1)2的最大值是0
其中错误的个数是( )
A.1
B.2
C.3
D.4
【分析】直接利用偶次方的性质分别分析得出答案.
【解答】解:①a2+(b+1)2总是非负数,故此选错误;
②a2+b2+1总是正数,正确;
③9+(a﹣b)2的最小值为9,正确;
④1﹣(ab+1)2的最大值是1,故此选项错误.
故选:B.
【点评】此题主要考查了非负数的性质,正确掌握偶次方的性质是解题关键.
5.(4分)当a<0时,下列式子成立的个数是( )
①|a|=a;②a2>0;③a3<0;④a2=(﹣a)2;⑤a3=﹣a3
A.1个
B.2个
C.3个
D.4个
【分析】根据a<0,可以判断题目中各个小题中的结论是否成立,本题得以解决.
【解答】解:当a<0时,
|a|=﹣a,故①错误,
a2>0,故②正确,
a3<0,故③正确,
a2=(﹣a)2,故④正确,
﹣a3>0,a3≠﹣a3,故⑤错误,
故选:C.
【点评】本题考查有理数的乘方、非负数的性质,解答本题的关键是明确题意,可以判断各个小题中的结论是否成立.
6.(4分)已知x,y满足|x﹣3|+(y+4)2=0,则代数式(x+y)2018的值为( )
A.﹣1
B.1
C.2018
D.﹣2018
【分析】直接利用绝对值的性质以及偶次方的性质得出x,y的值,进而得出答案.
【解答】解:∵|x﹣3|+(y+4)2=0,
∴x=3,y=﹣4,
∴(x+y)2018=1.
故选:B.
【点评】此题主要考查了非负数的性质,正确把握相关定义是解题关键.
7.(4分)若|m﹣1|+n2+6n+9=0,那么m、n的值分别为( )
A.m=1,n=﹣3
B.m=﹣1,n=﹣3
C.m=﹣1,n=3
D.m=1,n=3
【分析】直接利用绝对值的性质以及非负数的性质得出m,n的值即可.
【解答】解:∵|m﹣1|+n2+6n+9=0,
∴m﹣1=0,n2+6n+9=0,
∴m=1,n=﹣3,
故选:A.
【点评】此题主要考查了非负数的性质,正确把握定义是解题关键.
8.(4分)据慈利红网消息,今年“十一”假期,慈利县各景点共接待游客29.15万人次,将29.15万用科学记数法表示为( )
A.29.15×104
B.2.915×104
C.2.915×105
D.2.915×106
【分析】科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值>10时,n是正数;当原数的绝对值<1时,n是负数.
【解答】解:29.15万=2.915×105,
故选:C.
【点评】此题考查科学记数法的表示方法.科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数,表示时关键要正确确定a的值以及n的值.
9.(4分)用百度搜索关键词“十九大”,百度为我们找到相关结果约18
600
000个,把18
600
000这个数用科学记数法表示为( )
A.0.186×108
B.1.86×107
C.18.6×106
D.186×105
【分析】根据科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值>10时,n是正数;当原数的绝对值<1时,n是负数.
【解答】解:18
600
000=1.86×107,
故选:B.
【点评】本题考查科学记数法的表示方法.科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数,表示时关键要正确确定a的值以及n的值.
10.(4分)据相关报道,开展精准扶贫户工作五年来,我国约有5500万人摆脱贫困,国家发放扶贫资金共375亿元.将375亿用科学记数法表示为( )
A.375×107
B.3.75×1010
C.3.75×109
D.37.5×108
【分析】科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值>1时,n是正数;当原数的绝对值<1时,n是负数.
【解答】解:将375亿用科学记数法表示为3.75×1010.
故选:B.
【点评】此题考查科学记数法的表示方法.科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数,表示时关键要正确确定a的值以及n的值.
二、填空题(
本大题共5小题,共20.0分)
11.(4分)若|a+1|+(b﹣2)2=0,则(a+b)3+a5的值为 0 .
【分析】先根据已知条件可求a、b的值,然后再把a、b的值代入所求代数式计算即可.
【解答】解:∵|a+1|+(b﹣2)2=0,
∴a+1=0,b﹣2=0,
∴a=﹣1,b=2,
∴a+b=1,
∴(a+b)3+a5=1+(﹣1)=0,
故答案为:0.
【点评】本题考查了非负数的性质、代数式求值.解题的关键是先求出a、b的值.当几个非负数相加和为0时,则其中的每一项都必须等于0.
12.(4分)《九章算术》是中国古代第一部数学专著,不仅最早提到分数问题,也首先记录了盈不足等问题,在第七章“盈不足”中有这样一个问题:“今有蒲生一日,长三尺;莞生一日,长一尺.蒲生日自半,莞生日自倍.问几何日而长等?”其意思是“有蒲和莞两种植物,蒲第一日长了3尺,莞第一日长了1尺,以后蒲每日生长的长度是前一日的一半,莞每日生长的长度是前一日的2倍,问几日蒲、莞上涨的长度相等.”
请计算出第三日后,蒲、莞的长度相差为 尺.
【分析】根据题意求出两种植物生长长度的规律即可求解.
【解答】解:(1)设:日蒲、莞上涨的长度相等
有题意得:蒲,第x日上涨长度为:3×21﹣x;莞,第x日上涨长度为:1×2x﹣1,
则:3×21﹣x=1×2x﹣1,解得:x≈2.6.
答:2.6日蒲、莞上涨的长度相等
(2)蒲第3日后上涨长度为:,
莞,第3日上涨长度为:7,
二者差为尺,
故答案是.
【点评】本题考查的是有理数的乘方,重点是要求出两种植物生长长度的规律,是一道难度较大的题目.
13.(4分)南海海域面积约为3500000平方千米,该面积用科学记数法应表示为 3.5×106 平方千米.
【分析】科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值>10时,n是正数;当原数的绝对值<1时,n是负数.
【解答】解:3500000用科学记数法表示为3.5×106,
故答案为:3.5×106.
【点评】此题考查科学记数法的表示方法.科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数,表示时关键要正确确定a的值以及n的值.
14.(4分)40.02万精确到 百 位,1.2349×105按四舍五入精确到千位得到的近似数为 1.23×105 .
【分析】根据近似数的精确度求解.
【解答】解:40.02万精确到百位,1.2349×105按四舍五入精确到千位得到的近似数为1.23×105,
故答案为:百,1.23×105.
【点评】本题考查了近似数和有效数字:近似数与精确数的接近程度,可以用精确度表示.一般有,精确到哪一位,保留几个有效数字等说法.从一个数的左边第一个不是0的数字起到末位数字止,所有的数字都是这个数的有效数字.
15.(4分)一种电子计算机每秒可以进行3×108次运算,它工作2×102秒可进行 6×1010 次运算.
【分析】根据同底数幂的乘法运算法则以及积的乘方运算得出即可.
【解答】解:∵一种电子计算机每秒可以进行3×108次运算,
∴它工作2×102秒可进行:3×108×2×102=6×1010(次).
故答案为:6×1010.
【点评】此题主要考查了科学记数法﹣表示较大的数,积的乘方以及同底数幂的乘法运算法则,熟练掌握预算法则是解题关键.
三、解答题(
本大题共5小题,共40.0分)
16.(8分)阅读下列各式:(a×b)2=a2×b2,(a×b)3=a3×b3,(a×b)4=a4×b4(a×b)5=a5×b5……回答下列三个问题:
(1)猜想:(a×b)n= an×bn .
(2)请用我们学过的知识说明上式成立的理由.
(3)请计算:(﹣0.125)2019×22018×42017
【分析】(1)根据材料中的各数的值找出规律即可解答;
(2)利用同底数幂的乘法定义进行证明;
(3)根据(2)中的规律计算出所求代数式的值即可.
【解答】解:(1)猜想:(a×b)n=an×bn.
故答案是:an×bn.
(2)理由:
(3)
【点评】本题考查的是有理数乘方的法则,解答此题的关键是根据材料中各数的特点找出规律,再根据此规律进行解答.
17.(8分)若有理数a、b、c满足:(a﹣1)2+(2a﹣b)4+|3c+1|=0.求(c﹣a)2+c3﹣b的值.
【分析】根据已知等式,利用非负数的性质求出a,b,c的值,即可确定出(c﹣a)2+c3﹣b的值.
【解答】解:∵(a﹣1)2+(2a﹣b)4+|3c+1|=0,
∴a﹣1=0,2a﹣b=0,3c+1=0,
∴a=1,b=2,c=﹣,
∴(c﹣a)2+c3﹣b=(﹣﹣1)2+(﹣﹣)3﹣2=﹣.
【点评】此题考查了代数式求值,以及非负数的性质,熟练掌握运算法则是解本题的关键.
18.(8分)我们常用的数是十进制数,如4657=4×103+6×102+5×101+7×100,数要用10个数码(又叫数字):0、1、2、3、4、5、6、7、8、9,在电子计算机中用的二进制,只要两个数码:0和1,如二进制中110=1×22+1×21+0×20等于十进制的数6,110101=1×25+1×24+0×23+1×22+0×21+1×20等于十进制的数53.那么二进制中的数101011等于十进制中的哪个数?
【分析】利用新定义得到101011=1×25+0×24+1×23+0×22+1×21+1×20,然后根据乘方的定义进行计算.
【解答】解:101011=1×25+0×24+1×23+0×22+1×21+1×20=43,
所以二进制中的数101011等于十进制中的43.
【点评】本题考查了有理数的乘方:有理数乘方的定义:求n个相同因数积的运算,叫做乘方.
19.(8分)小明爸爸给小明出了一道题,说明他本月炒股的盈亏情况(单位:元)
股票
每股净赚(元)
股票
招商银行
+23
500
浙江医药
﹣(﹣2.8)
1000
晨光文具
﹣1.5
1500
金龙汽车
﹣1
2000
请你也来计算一下,小明爸爸本月投资炒股到底是赔了还是赚了?赔了或赚了多少元?
【分析】首先分别求出招商银行、浙江医药、晨光文具、金龙汽车这4种股票分别赚了多少钱;然后把它们相加,判断出投资者到底是赔了还是赚了,赔了或赚了多少元即可.
【解答】解:天河:500×23
+2.8×1000﹣1.5×1500﹣1.8×2000
=4000+2800﹣2250﹣3600
=950(元)
答:赚了,赚了950元.
【点评】此题主要考查了有理数的乘方的含义和求法,以及有理数的加减法的运算方法,要熟练掌握.
20.(8分)乐乐的爸爸投资股票,有一次乐乐发现爸爸持有股票的情况如表格所示:请你帮助分析:乐乐爸爸究竟是赚了还是赔了,赚或赔了多少元?
股票名称
每股净赚(元)
股数
天河
﹣22
500
北斗
+1.5
1000
白马
﹣4
1000
海湖
﹣(﹣2)
500
【分析】根据题意列出算式﹣22×500+1.5×1000﹣4×1000﹣(﹣2)×500,计算可得.
【解答】解:﹣22×500+1.5×1000﹣4×1000﹣(﹣2)×500
=﹣2000+1500﹣4000+1000
=﹣3500,
答:乐乐的爸爸赔了,赔了3500元.
【点评】本题主要考查有理数的混合运算,解题的关键是根据题意列出算式并熟练掌握有理数混合运算顺序及其法则.
第14页(共14页)
一、选择题(
本大题共10小题,共40.0分)
1.(4分)若(b+1)2+3|a﹣2|=0,则a﹣2b的值是( )
A.﹣4
B.0
C.4
D.2
2.(4分)关于﹣(﹣a)2的相反数,有下列说法:①等于a2;②等于(﹣a)2;③值可能为0;④值一定是正数.其中正确的有( )
A.1个
B.2个
C.3个
D.4个
3.(4分)下列结论中,错误的个数为( )
﹣(﹣2)2=4;﹣5÷=﹣5;;=﹣3;﹣33=﹣9.
A.2个
B.3个
C.4个
D.5个
4.(4分)若a、b有理数,下列判断:
①a2+(b+1)2总是正数;
②a2+b2+1总是正数;
③9+(a﹣b)2的最小值为9;
④1﹣(ab+1)2的最大值是0
其中错误的个数是( )
A.1
B.2
C.3
D.4
5.(4分)当a<0时,下列式子成立的个数是( )
①|a|=a;②a2>0;③a3<0;④a2=(﹣a)2;⑤a3=﹣a3
A.1个
B.2个
C.3个
D.4个
6.(4分)已知x,y满足|x﹣3|+(y+4)2=0,则代数式(x+y)2018的值为( )
A.﹣1
B.1
C.2018
D.﹣2018
7.(4分)若|m﹣1|+n2+6n+9=0,那么m、n的值分别为( )
A.m=1,n=﹣3
B.m=﹣1,n=﹣3
C.m=﹣1,n=3
D.m=1,n=3
8.(4分)据慈利红网消息,今年“十一”假期,慈利县各景点共接待游客29.15万人次,将29.15万用科学记数法表示为( )
A.29.15×104
B.2.915×104
C.2.915×105
D.2.915×106
9.(4分)用百度搜索关键词“十九大”,百度为我们找到相关结果约18
600
000个,把18
600
000这个数用科学记数法表示为( )
A.0.186×108
B.1.86×107
C.18.6×106
D.186×105
10.(4分)据相关报道,开展精准扶贫户工作五年来,我国约有5500万人摆脱贫困,国家发放扶贫资金共375亿元.将375亿用科学记数法表示为( )
A.375×107
B.3.75×1010
C.3.75×109
D.37.5×108
二、填空题(
本大题共5小题,共20.0分)
11.(4分)若|a+1|+(b﹣2)2=0,则(a+b)3+a5的值为
.
12.(4分)《九章算术》是中国古代第一部数学专著,不仅最早提到分数问题,也首先记录了盈不足等问题,在第七章“盈不足”中有这样一个问题:“今有蒲生一日,长三尺;莞生一日,长一尺.蒲生日自半,莞生日自倍.问几何日而长等?”其意思是“有蒲和莞两种植物,蒲第一日长了3尺,莞第一日长了1尺,以后蒲每日生长的长度是前一日的一半,莞每日生长的长度是前一日的2倍,问几日蒲、莞上涨的长度相等.”
请计算出第三日后,蒲、莞的长度相差为
尺.
13.(4分)南海海域面积约为3500000平方千米,该面积用科学记数法应表示为
平方千米.
14.(4分)40.02万精确到
位,1.2349×105按四舍五入精确到千位得到的近似数为
.
15.(4分)一种电子计算机每秒可以进行3×108次运算,它工作2×102秒可进行
次运算.
三、解答题(
本大题共5小题,共40.0分)
16.(8分)阅读下列各式:(a×b)2=a2×b2,(a×b)3=a3×b3,(a×b)4=a4×b4(a×b)5=a5×b5……回答下列三个问题:
(1)猜想:(a×b)n=
.
(2)请用我们学过的知识说明上式成立的理由.
(3)请计算:(﹣0.125)2019×22018×42017
17.(8分)若有理数a、b、c满足:(a﹣1)2+(2a﹣b)4+|3c+1|=0.求(c﹣a)2+c3﹣b的值.
18.(8分)我们常用的数是十进制数,如4657=4×103+6×102+5×101+7×100,数要用10个数码(又叫数字):0、1、2、3、4、5、6、7、8、9,在电子计算机中用的二进制,只要两个数码:0和1,如二进制中110=1×22+1×21+0×20等于十进制的数6,110101=1×25+1×24+0×23+1×22+0×21+1×20等于十进制的数53.那么二进制中的数101011等于十进制中的哪个数?
19.(8分)小明爸爸给小明出了一道题,说明他本月炒股的盈亏情况(单位:元)
股票
每股净赚(元)
股票
招商银行
+23
500
浙江医药
﹣(﹣2.8)
1000
晨光文具
﹣1.5
1500
金龙汽车
﹣1
2000
请你也来计算一下,小明爸爸本月投资炒股到底是赔了还是赚了?赔了或赚了多少元?
20.(8分)乐乐的爸爸投资股票,有一次乐乐发现爸爸持有股票的情况如表格所示:请你帮助分析:乐乐爸爸究竟是赚了还是赔了,赚或赔了多少元?
股票名称
每股净赚(元)
股数
天河
﹣22
500
北斗
+1.5
1000
白马
﹣4
1000
海湖
﹣(﹣2)
500
参考答案与试题解析
一、选择题(
本大题共10小题,共40.0分)
1.(4分)若(b+1)2+3|a﹣2|=0,则a﹣2b的值是( )
A.﹣4
B.0
C.4
D.2
【分析】首先根据非负数的性质可求出a、b的值,进而可求出a﹣2b的值.
【解答】解:∵(b+1)2+3|a﹣2|=0,
∴a﹣2=0,b+1=0,
解得a=2,b=﹣1;
∴a﹣2b=2﹣(﹣2)=4.
故选:C.
【点评】此题主要考查了非负数的性质,初中阶段有三种类型的非负数:绝对值、偶次方、二次根式(算术平方根).当它们相加和为0时,必须满足其中的每一项都等于0.
2.(4分)关于﹣(﹣a)2的相反数,有下列说法:①等于a2;②等于(﹣a)2;③值可能为0;④值一定是正数.其中正确的有( )
A.1个
B.2个
C.3个
D.4个
【解答】解:①∵﹣(﹣a)2=﹣a2,∴它的相反数是a2.显然是正确的.
②∵(﹣a)2=a2,∴也是正确的.
③当a=0时,a2=0,∴原式的值可能为0,也是正确的.
④是错误的,没有考虑0.
故有3个是正确的.
故选:C.
【点评】注意0既不是正数也不是负数,0的相反数是0.
3.(4分)下列结论中,错误的个数为( )
﹣(﹣2)2=4;﹣5÷=﹣5;;=﹣3;﹣33=﹣9.
A.2个
B.3个
C.4个
D.5个
【分析】根据有理数的乘方法则,乘法法则一一计算即可即可判断;
【解答】解:﹣(﹣2)2=4;错误,应该是﹣4;
﹣5÷=﹣5;错误,应该是﹣25;
;错误,应该是;
=﹣3;正确;
﹣33=﹣9.错误,应该是﹣27.
故选:C.
【点评】本题考查有理数的乘方,解题的关键是熟练掌握有理数的乘法法则,乘法法则,属于中考常考题型.
4.(4分)若a、b有理数,下列判断:
①a2+(b+1)2总是正数;
②a2+b2+1总是正数;
③9+(a﹣b)2的最小值为9;
④1﹣(ab+1)2的最大值是0
其中错误的个数是( )
A.1
B.2
C.3
D.4
【分析】直接利用偶次方的性质分别分析得出答案.
【解答】解:①a2+(b+1)2总是非负数,故此选错误;
②a2+b2+1总是正数,正确;
③9+(a﹣b)2的最小值为9,正确;
④1﹣(ab+1)2的最大值是1,故此选项错误.
故选:B.
【点评】此题主要考查了非负数的性质,正确掌握偶次方的性质是解题关键.
5.(4分)当a<0时,下列式子成立的个数是( )
①|a|=a;②a2>0;③a3<0;④a2=(﹣a)2;⑤a3=﹣a3
A.1个
B.2个
C.3个
D.4个
【分析】根据a<0,可以判断题目中各个小题中的结论是否成立,本题得以解决.
【解答】解:当a<0时,
|a|=﹣a,故①错误,
a2>0,故②正确,
a3<0,故③正确,
a2=(﹣a)2,故④正确,
﹣a3>0,a3≠﹣a3,故⑤错误,
故选:C.
【点评】本题考查有理数的乘方、非负数的性质,解答本题的关键是明确题意,可以判断各个小题中的结论是否成立.
6.(4分)已知x,y满足|x﹣3|+(y+4)2=0,则代数式(x+y)2018的值为( )
A.﹣1
B.1
C.2018
D.﹣2018
【分析】直接利用绝对值的性质以及偶次方的性质得出x,y的值,进而得出答案.
【解答】解:∵|x﹣3|+(y+4)2=0,
∴x=3,y=﹣4,
∴(x+y)2018=1.
故选:B.
【点评】此题主要考查了非负数的性质,正确把握相关定义是解题关键.
7.(4分)若|m﹣1|+n2+6n+9=0,那么m、n的值分别为( )
A.m=1,n=﹣3
B.m=﹣1,n=﹣3
C.m=﹣1,n=3
D.m=1,n=3
【分析】直接利用绝对值的性质以及非负数的性质得出m,n的值即可.
【解答】解:∵|m﹣1|+n2+6n+9=0,
∴m﹣1=0,n2+6n+9=0,
∴m=1,n=﹣3,
故选:A.
【点评】此题主要考查了非负数的性质,正确把握定义是解题关键.
8.(4分)据慈利红网消息,今年“十一”假期,慈利县各景点共接待游客29.15万人次,将29.15万用科学记数法表示为( )
A.29.15×104
B.2.915×104
C.2.915×105
D.2.915×106
【分析】科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值>10时,n是正数;当原数的绝对值<1时,n是负数.
【解答】解:29.15万=2.915×105,
故选:C.
【点评】此题考查科学记数法的表示方法.科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数,表示时关键要正确确定a的值以及n的值.
9.(4分)用百度搜索关键词“十九大”,百度为我们找到相关结果约18
600
000个,把18
600
000这个数用科学记数法表示为( )
A.0.186×108
B.1.86×107
C.18.6×106
D.186×105
【分析】根据科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值>10时,n是正数;当原数的绝对值<1时,n是负数.
【解答】解:18
600
000=1.86×107,
故选:B.
【点评】本题考查科学记数法的表示方法.科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数,表示时关键要正确确定a的值以及n的值.
10.(4分)据相关报道,开展精准扶贫户工作五年来,我国约有5500万人摆脱贫困,国家发放扶贫资金共375亿元.将375亿用科学记数法表示为( )
A.375×107
B.3.75×1010
C.3.75×109
D.37.5×108
【分析】科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值>1时,n是正数;当原数的绝对值<1时,n是负数.
【解答】解:将375亿用科学记数法表示为3.75×1010.
故选:B.
【点评】此题考查科学记数法的表示方法.科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数,表示时关键要正确确定a的值以及n的值.
二、填空题(
本大题共5小题,共20.0分)
11.(4分)若|a+1|+(b﹣2)2=0,则(a+b)3+a5的值为 0 .
【分析】先根据已知条件可求a、b的值,然后再把a、b的值代入所求代数式计算即可.
【解答】解:∵|a+1|+(b﹣2)2=0,
∴a+1=0,b﹣2=0,
∴a=﹣1,b=2,
∴a+b=1,
∴(a+b)3+a5=1+(﹣1)=0,
故答案为:0.
【点评】本题考查了非负数的性质、代数式求值.解题的关键是先求出a、b的值.当几个非负数相加和为0时,则其中的每一项都必须等于0.
12.(4分)《九章算术》是中国古代第一部数学专著,不仅最早提到分数问题,也首先记录了盈不足等问题,在第七章“盈不足”中有这样一个问题:“今有蒲生一日,长三尺;莞生一日,长一尺.蒲生日自半,莞生日自倍.问几何日而长等?”其意思是“有蒲和莞两种植物,蒲第一日长了3尺,莞第一日长了1尺,以后蒲每日生长的长度是前一日的一半,莞每日生长的长度是前一日的2倍,问几日蒲、莞上涨的长度相等.”
请计算出第三日后,蒲、莞的长度相差为 尺.
【分析】根据题意求出两种植物生长长度的规律即可求解.
【解答】解:(1)设:日蒲、莞上涨的长度相等
有题意得:蒲,第x日上涨长度为:3×21﹣x;莞,第x日上涨长度为:1×2x﹣1,
则:3×21﹣x=1×2x﹣1,解得:x≈2.6.
答:2.6日蒲、莞上涨的长度相等
(2)蒲第3日后上涨长度为:,
莞,第3日上涨长度为:7,
二者差为尺,
故答案是.
【点评】本题考查的是有理数的乘方,重点是要求出两种植物生长长度的规律,是一道难度较大的题目.
13.(4分)南海海域面积约为3500000平方千米,该面积用科学记数法应表示为 3.5×106 平方千米.
【分析】科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值>10时,n是正数;当原数的绝对值<1时,n是负数.
【解答】解:3500000用科学记数法表示为3.5×106,
故答案为:3.5×106.
【点评】此题考查科学记数法的表示方法.科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数,表示时关键要正确确定a的值以及n的值.
14.(4分)40.02万精确到 百 位,1.2349×105按四舍五入精确到千位得到的近似数为 1.23×105 .
【分析】根据近似数的精确度求解.
【解答】解:40.02万精确到百位,1.2349×105按四舍五入精确到千位得到的近似数为1.23×105,
故答案为:百,1.23×105.
【点评】本题考查了近似数和有效数字:近似数与精确数的接近程度,可以用精确度表示.一般有,精确到哪一位,保留几个有效数字等说法.从一个数的左边第一个不是0的数字起到末位数字止,所有的数字都是这个数的有效数字.
15.(4分)一种电子计算机每秒可以进行3×108次运算,它工作2×102秒可进行 6×1010 次运算.
【分析】根据同底数幂的乘法运算法则以及积的乘方运算得出即可.
【解答】解:∵一种电子计算机每秒可以进行3×108次运算,
∴它工作2×102秒可进行:3×108×2×102=6×1010(次).
故答案为:6×1010.
【点评】此题主要考查了科学记数法﹣表示较大的数,积的乘方以及同底数幂的乘法运算法则,熟练掌握预算法则是解题关键.
三、解答题(
本大题共5小题,共40.0分)
16.(8分)阅读下列各式:(a×b)2=a2×b2,(a×b)3=a3×b3,(a×b)4=a4×b4(a×b)5=a5×b5……回答下列三个问题:
(1)猜想:(a×b)n= an×bn .
(2)请用我们学过的知识说明上式成立的理由.
(3)请计算:(﹣0.125)2019×22018×42017
【分析】(1)根据材料中的各数的值找出规律即可解答;
(2)利用同底数幂的乘法定义进行证明;
(3)根据(2)中的规律计算出所求代数式的值即可.
【解答】解:(1)猜想:(a×b)n=an×bn.
故答案是:an×bn.
(2)理由:
(3)
【点评】本题考查的是有理数乘方的法则,解答此题的关键是根据材料中各数的特点找出规律,再根据此规律进行解答.
17.(8分)若有理数a、b、c满足:(a﹣1)2+(2a﹣b)4+|3c+1|=0.求(c﹣a)2+c3﹣b的值.
【分析】根据已知等式,利用非负数的性质求出a,b,c的值,即可确定出(c﹣a)2+c3﹣b的值.
【解答】解:∵(a﹣1)2+(2a﹣b)4+|3c+1|=0,
∴a﹣1=0,2a﹣b=0,3c+1=0,
∴a=1,b=2,c=﹣,
∴(c﹣a)2+c3﹣b=(﹣﹣1)2+(﹣﹣)3﹣2=﹣.
【点评】此题考查了代数式求值,以及非负数的性质,熟练掌握运算法则是解本题的关键.
18.(8分)我们常用的数是十进制数,如4657=4×103+6×102+5×101+7×100,数要用10个数码(又叫数字):0、1、2、3、4、5、6、7、8、9,在电子计算机中用的二进制,只要两个数码:0和1,如二进制中110=1×22+1×21+0×20等于十进制的数6,110101=1×25+1×24+0×23+1×22+0×21+1×20等于十进制的数53.那么二进制中的数101011等于十进制中的哪个数?
【分析】利用新定义得到101011=1×25+0×24+1×23+0×22+1×21+1×20,然后根据乘方的定义进行计算.
【解答】解:101011=1×25+0×24+1×23+0×22+1×21+1×20=43,
所以二进制中的数101011等于十进制中的43.
【点评】本题考查了有理数的乘方:有理数乘方的定义:求n个相同因数积的运算,叫做乘方.
19.(8分)小明爸爸给小明出了一道题,说明他本月炒股的盈亏情况(单位:元)
股票
每股净赚(元)
股票
招商银行
+23
500
浙江医药
﹣(﹣2.8)
1000
晨光文具
﹣1.5
1500
金龙汽车
﹣1
2000
请你也来计算一下,小明爸爸本月投资炒股到底是赔了还是赚了?赔了或赚了多少元?
【分析】首先分别求出招商银行、浙江医药、晨光文具、金龙汽车这4种股票分别赚了多少钱;然后把它们相加,判断出投资者到底是赔了还是赚了,赔了或赚了多少元即可.
【解答】解:天河:500×23
+2.8×1000﹣1.5×1500﹣1.8×2000
=4000+2800﹣2250﹣3600
=950(元)
答:赚了,赚了950元.
【点评】此题主要考查了有理数的乘方的含义和求法,以及有理数的加减法的运算方法,要熟练掌握.
20.(8分)乐乐的爸爸投资股票,有一次乐乐发现爸爸持有股票的情况如表格所示:请你帮助分析:乐乐爸爸究竟是赚了还是赔了,赚或赔了多少元?
股票名称
每股净赚(元)
股数
天河
﹣22
500
北斗
+1.5
1000
白马
﹣4
1000
海湖
﹣(﹣2)
500
【分析】根据题意列出算式﹣22×500+1.5×1000﹣4×1000﹣(﹣2)×500,计算可得.
【解答】解:﹣22×500+1.5×1000﹣4×1000﹣(﹣2)×500
=﹣2000+1500﹣4000+1000
=﹣3500,
答:乐乐的爸爸赔了,赔了3500元.
【点评】本题主要考查有理数的混合运算,解题的关键是根据题意列出算式并熟练掌握有理数混合运算顺序及其法则.
第14页(共14页)
同课章节目录
