13讲.多边形的面积:梯形的面积(教师版同步讲义)-2021-2022学年数学五年级上册-人教版
文档属性
| 名称 | 13讲.多边形的面积:梯形的面积(教师版同步讲义)-2021-2022学年数学五年级上册-人教版 |
|
|
| 格式 | zip | ||
| 文件大小 | 324.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-20 09:31:11 | ||
图片预览





文档简介
多边形面积
第
2节
梯形的面积
【知识梳理】
梯形面积=(上底+下底)×高÷2
梯形上底=面积×2÷高-下底
梯形下底=面积×2÷高-上底
梯形高=面积×2÷底
【诊断自测】
求梯形面积公式的字母表示:
求梯形上底的公式是:
3、一个梯形的上底是9分米,下底是10分米,高是4分米,面积是( )平方分米。
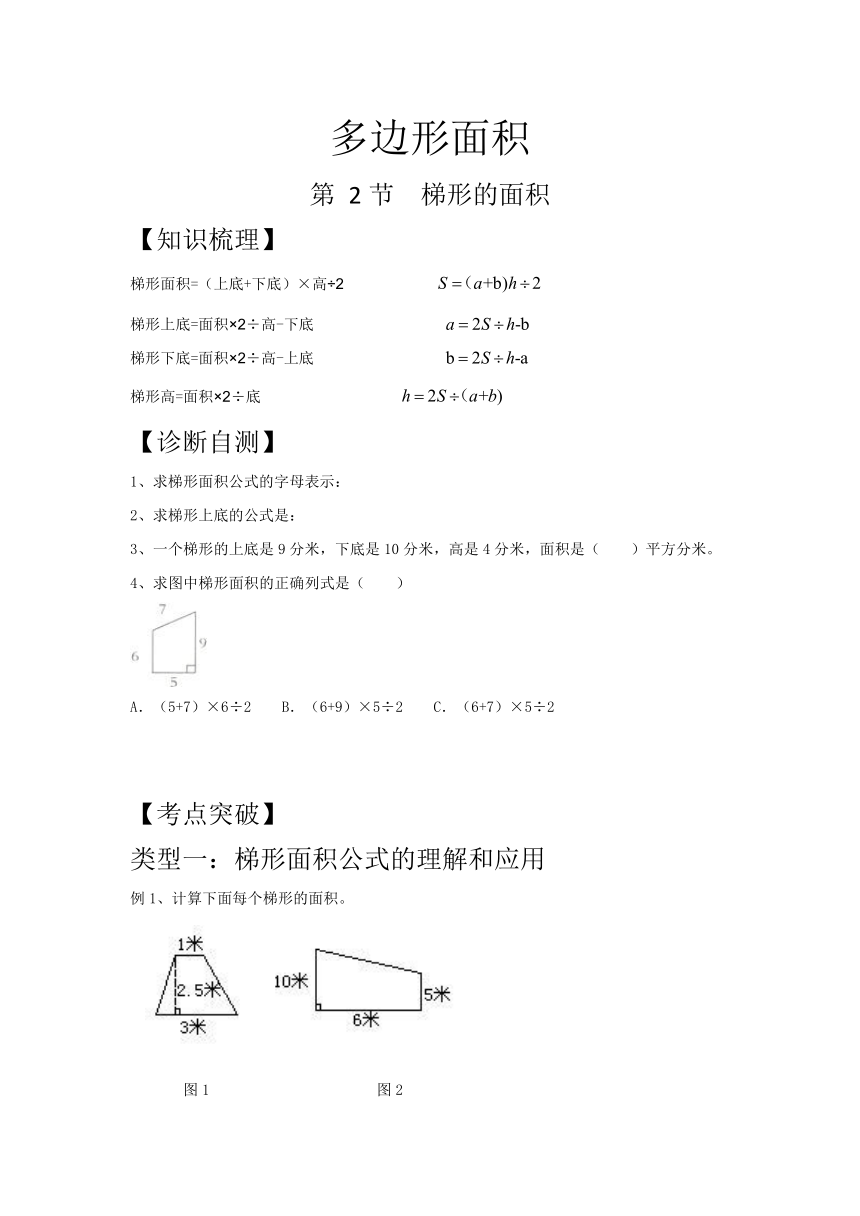
4、求图中梯形面积的正确列式是( )
A.(5+7)×6÷2
B.(6+9)×5÷2
C.(6+7)×5÷2
【考点突破】
类型一:梯形面积公式的理解和应用
例1、计算下面每个梯形的面积。
图1
图2
答案:5平方米、45平方米
解析:正确计算梯形的面积,要准确找出梯形的上底、下底和高,再根据梯形的面积计算进行计算。
图1的上底是1米,下底是3米,高是2.5米,面积是(1+3)×2.5÷2=5(平方米)
图2的上底是5米,下底是10米,高是6米,面积是(5+10)×6÷2=45(平方米)
类型二:应用梯形面积公式解决实际问题
例2、一条新挖的渠道,横截面是梯形(如下图)。渠口宽2.8米,渠底宽1.4米,渠深1.2
米。它的横截面积是多少平方米?
答案:2.52平方米
解析:这道题考查的是梯形的面积在实际中的运用。重点是要知道图中要计算的横截面的面
积是一个梯形,只要找到梯形的上底、下底和高就可以顺利计算出图中横截面的面积是
多少了。
例3、一个自选商店门口的装饰牌是等腰梯形(如图).油漆这块装饰牌,80千克油漆够不
够?(只油漆一面,每平方米需要用油漆1千克.)
(14+26)×4÷2×1=80(千克);
例4、如图:在一个梯形的果园上铺一条平行四边形小路,小路的底是3米,高是10米,
每3平方米种植一棵果树,这块地共种多少棵果树?
(15+23)×10÷2-3×10=160÷3≈53(棵),
例5、一块梯形麦田,上底是35m,下底是25m,面积是1140,高是多少米?
答案:38m
解析:梯形的面积计算公式是,利用乘除法各部分之间的关系,可以得出梯形的高=面积×2÷(上底+下底),即。
例6、有一块菜地为梯形,上底是13米,下底17米,高是20米,去年共收白菜6900千克,平均每平方米收白菜多少千克?
答案:23千克
解析:6900÷[(13+17)×20÷2]=23(千克)
类型三:梯形面积与其他图形的面积关系
例7、如右图,左边梯形和右边三角形的面积相等,求三角形的底是多少。(单位:cm)
答案:7cm
解析:从已知条件“左边梯形和右边三角形的面积相等”可以推出:三角形的面积等于整个图形面积的一半,这样三角形的面积可以直接求出。最后利用三角形面积公式求出三角形的底。
答:三角形的是7cm。
类型四:应用上底与下底的和整体直接求面积
例8、李奶奶利用一面墙围成了如下图所示的小菜园,篱笆长64m,求李奶奶家的小菜园的面积。
答案:315m2
解析:小菜园是一个梯形,就是求梯形的面积。梯形面积=(上底+下底)×高÷2。已知了梯形四边的长度和、高的长度和斜边的长度,用四边的长度和-高的长度-斜边的长度=上底+下底,再用梯形面积公式即可求得面积。
上底+下底=64-19=45(m)
菜园面积=45×14÷2=315()
类型五:综合理解与应用
例9、如图,求直角梯形的面积.
答案:200平方厘米
解析:20×20÷2=200(平方厘米)
例10、在图中,梯形的下底是17.5厘米,高是5厘米,两个底角都是45°,求梯形的面积.
答案:62.5平方厘米
解析:7.5-5×2=7.5(厘米),
(7.5+17.5×5÷2)=62.5(平方厘米)
【易错精选】
一个梯形的下底是上底的1.5倍,高是18厘米,面积是540平方厘米,则这个梯形的上底是多少厘米。
一个梯形高与两底的乘积分别是18平方厘米和25平方厘米.这个梯形的面积是多少平方厘米?
3、有一块梯形果园,下底80米,比上底长20米,高50米,平均每7平方米栽一棵果树,这块地共可栽多少棵果树?
一块梯形广告牌,上底8米,下底12米,高10米.现将它双面刷油漆,如果每平方米用油漆0.2千克,这块广告牌需要多少千克油漆?
5、下面平行线中的三个图形,它们的面积从大到小排列是(
)
【精华提炼】
【总结】
梯形的面积=(上底+下底)×高÷2。如果用a、b、h和S分别表示梯形的上底、下底、高的面积,那么梯形的面积计算公式可以写成S=(a+b)h÷2。已知四个变量中任意三个量就可以求得未知的量。
【本节训练】
训练【1】
一堆同样的钢管,最上层9根,最下层21根,共13层,这堆钢管共有( )根
训练【2】如图,李爷爷在自已的院墙边用篱笆围了一个牛栏,篱笆全长20.5米,求牛栏的占面积是多少?
训练【3】一条河的横截面是一个梯形,梯形的上底是3米,下底是10米,高是2米,求这个梯形横截面的面积是多少平方米?
训练【4】用56米长的篱笆在靠墙的地方围一块地(如图)种菜,这块菜地的面积是多少平方米?
基础巩固
一、填空。
1.
梯形有(
)条高。
2.
(
)和(
)可以拼成平行四边形。拼成的平行四边形的底等于梯形的(
),平行四边形的高等于梯形的(
),所以每个梯形的面积等于平行四边形面积的(
),因此,梯形的面积等于(
),字母表示为(
)。
二、判断。
1.
两个梯形一定能拼成一个平行四边形。(
)
2.
梯形的面积等于平行四边形面积的一半。(
)
3.
梯形只有一组对边平行。(
)
4.
梯形的高越大,面积就越大。
(
)
三、选择。
1.
两个完全一样的梯形一定能拼成一个(
)。
A.长方形
B.平行四边形
C.三角形
2.
求右面梯形的面积,正确的列式是(
)。
A.(4+8)×3÷2
B.(4+8)×5÷2
C.(3+5)×4÷2
3.
一个梯形的上底和下底分别扩大到原来的3倍,高不变,它的面积扩大到原来的(
)倍。
A.9
B.6
C.3
四、计算下面梯形的面积。(单位:cm)
五、
解决问题。(每题8分,共24分)
(1)“银苏号”滑翔机模型的尾翼是由两个完全相同的梯形组成的。它的面积是多少?
(2)
一个梯形的上底是10dm,比下底短2dm,比高长5dm,它的面积是多少平方分米?
(3)
一堆圆木,最上层有3根,最下层有10根,每相邻的两层相差一根,这堆圆木共有多少根?
六、综合能力练
1.【综合运用题】一块街头广告牌是个等腰梯形,上底是4m,下底是6m,高是
2.5
m。
(1)
在它的正、反面刷油漆,刷油漆的面积有多大?(6分)
(2)
每平方米要用油漆0.6
kg,每千克油漆18.5元,一共需要多少元钱?(6分)
2.【探究题】下列各图阴影部分面积占整个图形面积一半的有(
)。(7分)
①
②
③
④
3.【潜能开发题】一块木板是直角梯形,它的上底是25dm,如果下底减少15dm,它就变成了正方形。求这块木板的面积。(7分)
巅峰突破
1、一个梯形,如果上底延长6cm,就成了一个正方形,面积增加了30cm2。那么原来梯形的面积是多少?
2、如图,求梯形ABCD的面积.如果用虚线将梯形分成面积相等的两部分,那么AE的长度是多少厘米?
3、、如图,梯形的上底是3厘米,下底是5厘米,直角三角形(阴影)的面积是4.5平方厘米。求梯形的面积。
4、如图,在梯形ABCD中,BC=2AD,已知阴影部分面积为120cm2,求梯形ABCD的面积.
5、如图所示,E,F,G,H分别是四边形各边中点,EG与FH交于点O,s1,s2,s3及
S4分别表示四个小四边形的面积.试比较
s1+s3与
s2+s4的大小?
参考答案
【诊断自测】
1、;
2、;
3、38;
4、B
【本节训练】
练习1、(9+21)×13÷2=195(根)
练习2、(20.5-8.5)×8.5÷2=51(平方米)
练习3、(3+10)×2÷2=13(平方米)
练习4、(56-12)×12÷2=264(平方米)
【易错精选】
1、24厘米
2、(18+25)÷2=21.5(平方厘米)
3、(80-20+80)×50÷7=1000(棵)
4、(8+12)×10÷2×2×0.2=40(千克)
5、③>②>①
基础巩固
一、填空
1.(1)无数
(2)A
C
上底十下底
高
一半
(上底十下底)×高÷
2
二、判断
1.×
2.×
3.√
4.×
三、选择
1.B
2.A
3.C
四、(3.1+5.4)×1.6÷2=6.8()
五、(1)(4+8)×20÷2×2=240()
(2)(10+2+10)×(10-5)÷2=55()
(3)(3+10)×(10-3+1)÷2=52(根)
六、
1.(1)(6+4)×2.5÷2×2=25()
(2)25×0.6×18.5=277.5(元)
2.①②④
3.下底:25+15=40(dm)
面积:(25+40)×25÷2=812.5()
巅峰突破
如图:
直角梯形的高为:30×2÷6=10(厘米),
直角梯形的面积为:10×10-30=100-30=70(平方厘米)
2、12-(7+12)÷2=12-9.5=2.5(厘米)
3、4.5×2÷3=3(厘米);(3+5)×3÷2=12(平方厘米)
4、根据题干分析可得:空白处的两个三角形可以转化到三角形ABD中,因为三角形ABD与
阴影部分的三角形高相等,BC=2AD,所以三角形ABD的面积是:120÷2=60(平方厘米),
120+60=180(平方厘米),答:这个梯形的面积是180平方厘米。
5、连接OA,OB,OC,OD,
在△AOB中,因为E是AB的中点,
所以△AOE和△BOE面积相等,
同理可得,
△AOH与△DOH面积相等,
△COG与△DOG面积相等,
△COF与△BOF面积相等,
所以△AOE+△AOH+△COG+△COF=△BOE+△DOH+△DOG+△BOF,
即:S1+S3=S2+S4,
答:s1+s3与
s2+s4的大小相等.
第
2节
梯形的面积
【知识梳理】
梯形面积=(上底+下底)×高÷2
梯形上底=面积×2÷高-下底
梯形下底=面积×2÷高-上底
梯形高=面积×2÷底
【诊断自测】
求梯形面积公式的字母表示:
求梯形上底的公式是:
3、一个梯形的上底是9分米,下底是10分米,高是4分米,面积是( )平方分米。
4、求图中梯形面积的正确列式是( )
A.(5+7)×6÷2
B.(6+9)×5÷2
C.(6+7)×5÷2
【考点突破】
类型一:梯形面积公式的理解和应用
例1、计算下面每个梯形的面积。
图1
图2
答案:5平方米、45平方米
解析:正确计算梯形的面积,要准确找出梯形的上底、下底和高,再根据梯形的面积计算进行计算。
图1的上底是1米,下底是3米,高是2.5米,面积是(1+3)×2.5÷2=5(平方米)
图2的上底是5米,下底是10米,高是6米,面积是(5+10)×6÷2=45(平方米)
类型二:应用梯形面积公式解决实际问题
例2、一条新挖的渠道,横截面是梯形(如下图)。渠口宽2.8米,渠底宽1.4米,渠深1.2
米。它的横截面积是多少平方米?
答案:2.52平方米
解析:这道题考查的是梯形的面积在实际中的运用。重点是要知道图中要计算的横截面的面
积是一个梯形,只要找到梯形的上底、下底和高就可以顺利计算出图中横截面的面积是
多少了。
例3、一个自选商店门口的装饰牌是等腰梯形(如图).油漆这块装饰牌,80千克油漆够不
够?(只油漆一面,每平方米需要用油漆1千克.)
(14+26)×4÷2×1=80(千克);
例4、如图:在一个梯形的果园上铺一条平行四边形小路,小路的底是3米,高是10米,
每3平方米种植一棵果树,这块地共种多少棵果树?
(15+23)×10÷2-3×10=160÷3≈53(棵),
例5、一块梯形麦田,上底是35m,下底是25m,面积是1140,高是多少米?
答案:38m
解析:梯形的面积计算公式是,利用乘除法各部分之间的关系,可以得出梯形的高=面积×2÷(上底+下底),即。
例6、有一块菜地为梯形,上底是13米,下底17米,高是20米,去年共收白菜6900千克,平均每平方米收白菜多少千克?
答案:23千克
解析:6900÷[(13+17)×20÷2]=23(千克)
类型三:梯形面积与其他图形的面积关系
例7、如右图,左边梯形和右边三角形的面积相等,求三角形的底是多少。(单位:cm)
答案:7cm
解析:从已知条件“左边梯形和右边三角形的面积相等”可以推出:三角形的面积等于整个图形面积的一半,这样三角形的面积可以直接求出。最后利用三角形面积公式求出三角形的底。
答:三角形的是7cm。
类型四:应用上底与下底的和整体直接求面积
例8、李奶奶利用一面墙围成了如下图所示的小菜园,篱笆长64m,求李奶奶家的小菜园的面积。
答案:315m2
解析:小菜园是一个梯形,就是求梯形的面积。梯形面积=(上底+下底)×高÷2。已知了梯形四边的长度和、高的长度和斜边的长度,用四边的长度和-高的长度-斜边的长度=上底+下底,再用梯形面积公式即可求得面积。
上底+下底=64-19=45(m)
菜园面积=45×14÷2=315()
类型五:综合理解与应用
例9、如图,求直角梯形的面积.
答案:200平方厘米
解析:20×20÷2=200(平方厘米)
例10、在图中,梯形的下底是17.5厘米,高是5厘米,两个底角都是45°,求梯形的面积.
答案:62.5平方厘米
解析:7.5-5×2=7.5(厘米),
(7.5+17.5×5÷2)=62.5(平方厘米)
【易错精选】
一个梯形的下底是上底的1.5倍,高是18厘米,面积是540平方厘米,则这个梯形的上底是多少厘米。
一个梯形高与两底的乘积分别是18平方厘米和25平方厘米.这个梯形的面积是多少平方厘米?
3、有一块梯形果园,下底80米,比上底长20米,高50米,平均每7平方米栽一棵果树,这块地共可栽多少棵果树?
一块梯形广告牌,上底8米,下底12米,高10米.现将它双面刷油漆,如果每平方米用油漆0.2千克,这块广告牌需要多少千克油漆?
5、下面平行线中的三个图形,它们的面积从大到小排列是(
)
【精华提炼】
【总结】
梯形的面积=(上底+下底)×高÷2。如果用a、b、h和S分别表示梯形的上底、下底、高的面积,那么梯形的面积计算公式可以写成S=(a+b)h÷2。已知四个变量中任意三个量就可以求得未知的量。
【本节训练】
训练【1】
一堆同样的钢管,最上层9根,最下层21根,共13层,这堆钢管共有( )根
训练【2】如图,李爷爷在自已的院墙边用篱笆围了一个牛栏,篱笆全长20.5米,求牛栏的占面积是多少?
训练【3】一条河的横截面是一个梯形,梯形的上底是3米,下底是10米,高是2米,求这个梯形横截面的面积是多少平方米?
训练【4】用56米长的篱笆在靠墙的地方围一块地(如图)种菜,这块菜地的面积是多少平方米?
基础巩固
一、填空。
1.
梯形有(
)条高。
2.
(
)和(
)可以拼成平行四边形。拼成的平行四边形的底等于梯形的(
),平行四边形的高等于梯形的(
),所以每个梯形的面积等于平行四边形面积的(
),因此,梯形的面积等于(
),字母表示为(
)。
二、判断。
1.
两个梯形一定能拼成一个平行四边形。(
)
2.
梯形的面积等于平行四边形面积的一半。(
)
3.
梯形只有一组对边平行。(
)
4.
梯形的高越大,面积就越大。
(
)
三、选择。
1.
两个完全一样的梯形一定能拼成一个(
)。
A.长方形
B.平行四边形
C.三角形
2.
求右面梯形的面积,正确的列式是(
)。
A.(4+8)×3÷2
B.(4+8)×5÷2
C.(3+5)×4÷2
3.
一个梯形的上底和下底分别扩大到原来的3倍,高不变,它的面积扩大到原来的(
)倍。
A.9
B.6
C.3
四、计算下面梯形的面积。(单位:cm)
五、
解决问题。(每题8分,共24分)
(1)“银苏号”滑翔机模型的尾翼是由两个完全相同的梯形组成的。它的面积是多少?
(2)
一个梯形的上底是10dm,比下底短2dm,比高长5dm,它的面积是多少平方分米?
(3)
一堆圆木,最上层有3根,最下层有10根,每相邻的两层相差一根,这堆圆木共有多少根?
六、综合能力练
1.【综合运用题】一块街头广告牌是个等腰梯形,上底是4m,下底是6m,高是
2.5
m。
(1)
在它的正、反面刷油漆,刷油漆的面积有多大?(6分)
(2)
每平方米要用油漆0.6
kg,每千克油漆18.5元,一共需要多少元钱?(6分)
2.【探究题】下列各图阴影部分面积占整个图形面积一半的有(
)。(7分)
①
②
③
④
3.【潜能开发题】一块木板是直角梯形,它的上底是25dm,如果下底减少15dm,它就变成了正方形。求这块木板的面积。(7分)
巅峰突破
1、一个梯形,如果上底延长6cm,就成了一个正方形,面积增加了30cm2。那么原来梯形的面积是多少?
2、如图,求梯形ABCD的面积.如果用虚线将梯形分成面积相等的两部分,那么AE的长度是多少厘米?
3、、如图,梯形的上底是3厘米,下底是5厘米,直角三角形(阴影)的面积是4.5平方厘米。求梯形的面积。
4、如图,在梯形ABCD中,BC=2AD,已知阴影部分面积为120cm2,求梯形ABCD的面积.
5、如图所示,E,F,G,H分别是四边形各边中点,EG与FH交于点O,s1,s2,s3及
S4分别表示四个小四边形的面积.试比较
s1+s3与
s2+s4的大小?
参考答案
【诊断自测】
1、;
2、;
3、38;
4、B
【本节训练】
练习1、(9+21)×13÷2=195(根)
练习2、(20.5-8.5)×8.5÷2=51(平方米)
练习3、(3+10)×2÷2=13(平方米)
练习4、(56-12)×12÷2=264(平方米)
【易错精选】
1、24厘米
2、(18+25)÷2=21.5(平方厘米)
3、(80-20+80)×50÷7=1000(棵)
4、(8+12)×10÷2×2×0.2=40(千克)
5、③>②>①
基础巩固
一、填空
1.(1)无数
(2)A
C
上底十下底
高
一半
(上底十下底)×高÷
2
二、判断
1.×
2.×
3.√
4.×
三、选择
1.B
2.A
3.C
四、(3.1+5.4)×1.6÷2=6.8()
五、(1)(4+8)×20÷2×2=240()
(2)(10+2+10)×(10-5)÷2=55()
(3)(3+10)×(10-3+1)÷2=52(根)
六、
1.(1)(6+4)×2.5÷2×2=25()
(2)25×0.6×18.5=277.5(元)
2.①②④
3.下底:25+15=40(dm)
面积:(25+40)×25÷2=812.5()
巅峰突破
如图:
直角梯形的高为:30×2÷6=10(厘米),
直角梯形的面积为:10×10-30=100-30=70(平方厘米)
2、12-(7+12)÷2=12-9.5=2.5(厘米)
3、4.5×2÷3=3(厘米);(3+5)×3÷2=12(平方厘米)
4、根据题干分析可得:空白处的两个三角形可以转化到三角形ABD中,因为三角形ABD与
阴影部分的三角形高相等,BC=2AD,所以三角形ABD的面积是:120÷2=60(平方厘米),
120+60=180(平方厘米),答:这个梯形的面积是180平方厘米。
5、连接OA,OB,OC,OD,
在△AOB中,因为E是AB的中点,
所以△AOE和△BOE面积相等,
同理可得,
△AOH与△DOH面积相等,
△COG与△DOG面积相等,
△COF与△BOF面积相等,
所以△AOE+△AOH+△COG+△COF=△BOE+△DOH+△DOG+△BOF,
即:S1+S3=S2+S4,
答:s1+s3与
s2+s4的大小相等.
