14讲.多边形的面积:三角形的面积(教师版同步讲义)-2021-2022学年数学五年级上册-人教版
文档属性
| 名称 | 14讲.多边形的面积:三角形的面积(教师版同步讲义)-2021-2022学年数学五年级上册-人教版 | 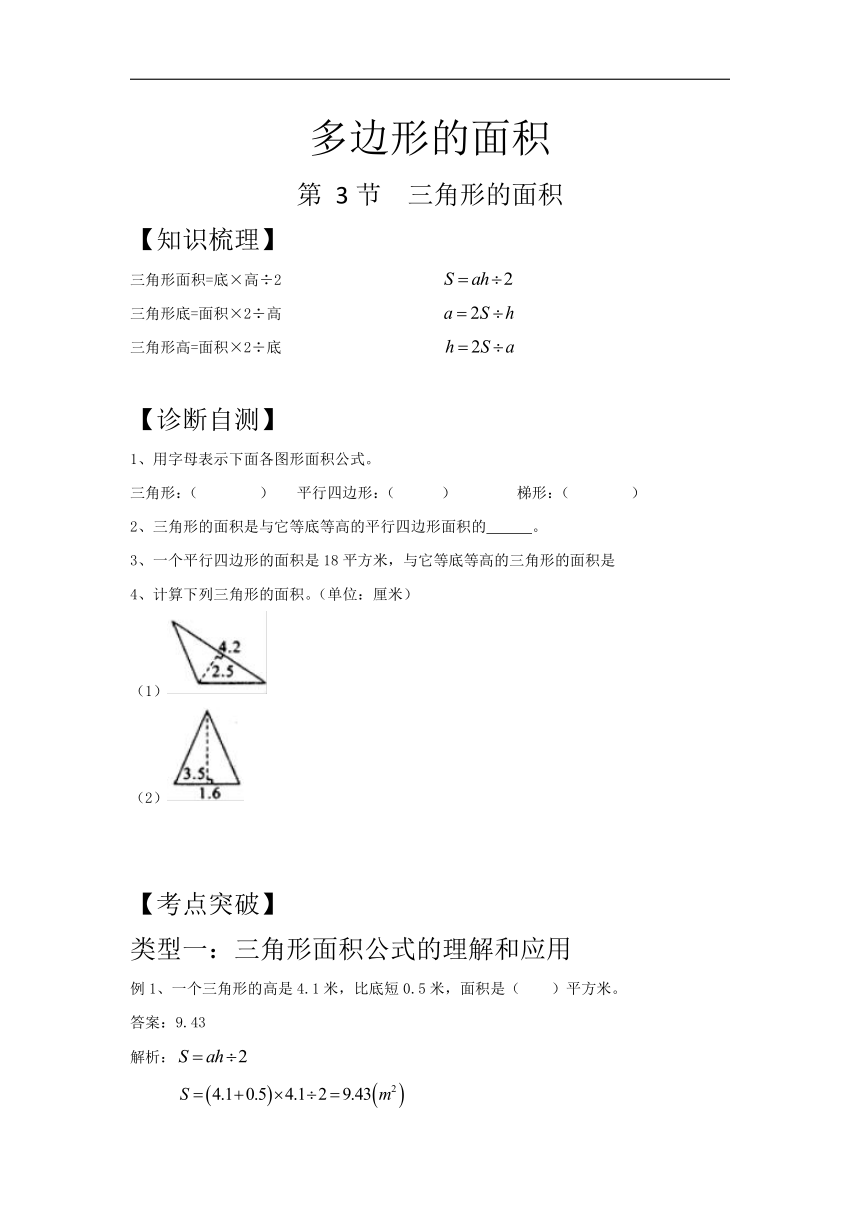 | |
| 格式 | zip | ||
| 文件大小 | 832.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-20 09:32:36 | ||
图片预览





文档简介
多边形的面积
第
3节
三角形的面积
【知识梳理】
三角形面积=底×高÷2
三角形底=面积×2÷高
三角形高=面积×2÷底
【诊断自测】
1、用字母表示下面各图形面积公式。?????
三角形:(????)?
平行四边形:(
)????梯形:(????)
2、三角形的面积是与它等底等高的平行四边形面积的
。
3、一个平行四边形的面积是18平方米,与它等底等高的三角形的面积是
4、计算下列三角形的面积。(单位:厘米)
(1)
(2)
【考点突破】
类型一:三角形面积公式的理解和应用
例1、一个三角形的高是4.1米,比底短0.5米,面积是(
)平方米。
答案:9.43
解析:
例2、一个三角形的面积是2.4平方分米,底是3分米,对应的高是(???
)。
答案:1.6dm
解析:
例3、一个等腰直角三角形,一条腰长3.5分米,这个三角形的面积是(
)平方分米。
答案:6.125
解析:直角三角形的两条直角边互为一组底和高,面积是直角边乘积的一半。
类型二:三角形面积相关解决问题
例4、一块长方形菜地,长60米,宽40米,在这块菜地中间有一个三角形水池,水池的底边长是16米,高是20米,这块菜地可以耕种的面积有多大?
答案:2240(平方米)
解析:
例5、一个梯形上底是5厘米,下底是8.2厘米,高是4.5厘米,如果在这个梯形中剪去一个最大的三角形,剩下的面积是多少平方厘米?
答案:11.25平方厘米
解析:画出图形,由题意可知,最大的三角形是以梯形下底的三角形,剩余部分是以梯形上底和高为底和高的三角形
S=
例6、一块三角形白菜地的面积是21.6平方米,它的底是5.4米,如果每棵白菜占地9平方分米,这块地一共有白菜(
)棵.
答案:240
解析:根据题目要求求解白菜的颗数。
(颗)
类型三:三角形面积与其他图形面积的关系
例7、下面梯形中两个阴影部分的面积相比,甲()乙。()应填(
)。
A.大于????B.小于????C.等于????D.无法确定
答案:C
解析:梯形的对角线将梯形分成的三角形,同底等高面积相等,减去重叠部分,得到甲乙面积相同。
类型四:三角形综合变形问题
例8、下图中正方形的边长为8厘米,CE为20厘米,梯形BCDF的面积是多少平方厘米?
答案:51.2平方厘米
解析:要求梯形的面积,关键是要求出上底FD的长度。连接FC后就能得到一个三角形EFC,用△EBC的面积减去△FBC的面积就能得到△EFC的面积:8×20÷2-8×8÷2=48(平方厘米)。FD=
48×2÷20=4.8(厘米)。所求梯形的面积就是
(4.8+8)×8÷2=51.2(平方厘米)。
答:梯形BCDF的面积是51.2平方厘米。
例9、右图是由八个边长是l厘米的小正方形拼成的长方形。求阴影部分的面积。
答案:5平方厘米
解析:阴影部分的面积是一个不能直接用公式求得的多边形,通过仔细观察可以发现,阴影部分的面积可以通过长方形的面积减去两个直角三角形的面积求得。阴影部分的面积=8×1-(3×1÷2)×2=5平方厘米
答:阴影部分的面积是5平方厘米。
例10、正方形ABCD的边长是8厘米,长方形DEFG的长DE是10厘米。问长方形的宽DG为多少厘米?
答案:6.4(厘米)
解析:求DG可以转化为求长方形的面积,题目已知正方形的边长和长方形的长的长度,可以得到正方形的面积,那如何利用正方形面积这个条件?观察发现正方形ABCD和长方形DEFG的重叠部分是一个多边形,这个多边形的面积无法求出,所以连结EC,既是正方形ABCD的一半,又是长方形EDGF的一半,就可以通过这个关系求出长方形的面积。
=8×8÷2=32(平方厘米)
=32×2=64(平方厘米)
DG=64÷10=6.4(厘米)
【易错精选】
下图阴影部分的面积是42平方分米,求梯形的面积。
2、判断:两个面积相等的三角形,底和高也相等.
(
)
3、一个三角形的底扩大2倍,高不变,它的面积扩大2倍。()
4、一个三角形和一个平行四边形的面积相等,底边也相等。已知平行四边形的高是6厘米,三角形的高是
(
)
A.3厘米
B.6厘米
C.12厘米
【精华提炼】
【总结】
1.三角形的面积等于它的底和该底上的高的积的一半。
2.同底(等底)同高(等高)的三角形面积相等,是与它等底等高的平行四边形面积的一半。
3.两个完全一样的三角形可以拼成一个平行四边形,两个完全一样的直角三角形可以拼成矩形和平行四边形,两个一样的等腰直角三角形可以拼成正方形和平行四边形。
【本节训练】
训练【1】一个三角形与一个平行四边形的面积和底都相等,平行四边形的高是3厘米,三角形的高是(
)厘米。
训练【2】求下图中阴影部分的面积。(单位:cm)
训练【3】求图中阴影部分的面积。(单位:厘米)
训练【4】在右图的梯形中剪下一个最大的三角形,剩下的图形是什么形状的?剩下的图形比剪下的图形小多少?
基础巩固
一、填空
1.
一个三角形的底是2.4米,高是27分米,同它等底等高的平行四边形面积是(
)平方分米。
2.
一个周长是92厘米的正方形,把它割补成一个平行四边形,它的面积是(
)。
3.
下图中的大正方形的边长是5厘米,小正方形的边长为4厘米,则阴影部分的面积为(
)平方厘米。
4.
一堆圆木,最底层有17根,最高层有5根,每相邻的两层间相差一根,这堆圆木共有(
)根。
5.
如下图是一个长方形,M是BC边中点,N是DC边中点,阴影部分占长方形面积的(
)。
一个三角形和一个平行四边形等底等高,这个三角形的面积是5.6平方米,平行四边形的面积是(
)平方米。
7.
三角形与平行四边形的面积相等,底也相等,平行四边形的高是5.8厘米,三角形的高是(
)分米。
8.
把一个边长是8分米的正方形拉成一个平行四边形,面积减少了4平方分米,这个平行四边形的高是(
)分米。
9.
两个完全相等的直角梯形正好拼成一个正方形,这个梯形的上底是8厘米,下底是12厘米,拼成后的正方形周长是(
)分米。
10.一个正方形的周长是20分米,它的面积与一个底是6.25分米的平行四边形的面积相等,这个平行四边形的高是(
)分米。
11.
用两个完全一样的梯形拼成一个面积是60平方厘米的平行四边形,如果梯形的上、下底之和是15厘米,高是(
)厘米。
12.
一个平行四边形分成一个三角形和一个梯形两部分(如图,单位:厘米)。已知它们的面积相差18.6平方厘米,则梯形的上底是(
)厘米。
13.一个周长是72厘米的正方形,把它割补成一个平行
四边形,它的面积是(
)平方厘米。
二、判断题
1.三角形的面积等于平行四边形面积的一半。
(
)
2.平行四边形的面积大于梯形面积。
(
)
3.任何一个梯形都可以分成两个等高的三角形。
(
)
4.两个面积相等的三角形一定能拼成一个平行四边形。
(
)
5.平行四边形的面积等于一个三角形面积的2倍。
(
)
6.
平行四边形的底是三角形的底的2倍,平行四边形的高是三角形的高的2倍,那么平行四边形的面积是三角形面积的4倍。
(
)
7.
梯形面积公式是“万能公式”。当上底和下底相等时,梯形公式就变成平行四边形公式;当上底为0时,又变成三角形公式;又因为平行四边形、长方形、正方形的特殊关系,因而又运用于长方形、正方形面积的计算。
(
)
8.
两个完全一样的直角梯形一定可以拼成一个(1)
平行四边形
(
)
(2)
长方形
(
)
(3)
等腰梯形
(
)
(4)
等腰三角形
(
)
(5)
直角梯形
(
)
三、计算面积
1.已知正方形ABCD的边长是7厘米,求正方形EFGH的面积。
2.有一个梯形,它的上底是5厘米,下底7厘米,如果只把上底增加3厘米,那么面积就增加4.5平方厘米。求原来梯形的面积。
3.如下图。已知大正方形的边长是12厘米,求中间最小正方形的面积。
巅峰突破
1.如图,正方形ABCD边长是6厘米,三角形AFD是正方形的一部分,三角形FCE的面积比三角形AFD大6平方厘米,求CE长多少厘米。
如图所示,三角形甲的面积与三角形乙的面积的关系是
A.大于??
B.小于??
C.等于
3、求下面组合图形的面积。(单位:cm)
如图,正方形ABCD
与正方形EFCH
的边长分别为3
和2
,若点B
、C
、F
在同一条直线上,点D
、C
、H
在同一条直线上,则三角形BDE
的面积为(????
)。
5、求图中四边形的面积。
参考答案
【诊断自测】
答案:1、;;
2、一半
3、9平方米
4、(1)4.2×2.5÷2=5.25(平方厘米)
(2)1.6×3.5÷2=2.8(平方厘米)
【本节训练】
1、6
2、8平方厘米
3、6厘米
4、解:从梯形的左下角到右上角剪下的三角形是最大的三角形,剩下的图形也是三角形;
25×12÷2﹣15×12÷2
=150﹣90
=60(平方厘米)
答:剩下的图形是三角形,剩下的图形比剪下的图形小60平方厘米.
【易错精选】
答案:1、60平方分米
2、错误
3、正确
4、C
基础巩固
一、填空
1.
648
2.
529平方厘米
提示:正方形与割补后的平行四边形的面积相同。
3.
8提示:两个正方形面积之和减去△ABC、△GBF、△CFE的面积。
4.
143
5.
6.
11.2
7.
1.16提示:三角形与平行四边形面积相等,底也相等,则三角形的高是平行四边形高的2倍。
8.
7.5提示:(8×8-4)÷8=7.5(分米)。
9.
8提示:(12+8)×4=80(厘米)=8(分米)。
10.
4提示:(分米)。
11.
4提示:60÷15=4(厘米),梯形上、下底之和即平行四边形的底。
12.
3提示:设梯形上底为,三角形的底为
=3。
13.
324提示:割补后正方形的面积与平行四边形面积相等。
二、判断
1.×
2.×
3.√
4.×
5.×
6.×
7.√
8.(1)
√
(2)
√
(3)√
(4)
×
(5)
×
三、计算面积
1.
7×7÷2=24.5(平方厘米)
2.
4.5×2÷3=3(厘米)
(5+7)×3÷2=18(平方厘米)
3.
12×12÷2÷2=36(平方厘米)
巅峰突破
1、解:设三角形AFD的面积为甲,三角形FCE的面积为乙,梯形ABCF的面积为丙。
乙=甲+6,丙+甲=6×6=36,可得
丙+乙=丙+甲+6=36+6=
42,即三角形ABE的面积等于42平方厘米。
BE=42×2÷6=14(厘米),CE=14-6=8(厘米)
C
4、答案:20平方厘米
解析:图中的这个多边形已知了两条边的长度和两个角度:90度和45度,要利用45度这个角度可以构造出以45度为内角的等腰直角三角形:通过切割或填补。
大等腰直角三角形的面积:7×7÷2=24.5(平方厘米)
小等腰直角三角形的面积:3×3÷2=4.5(平方厘米)
四边形的面积=24.5-4.5=20(平方厘米)
答:四边形的面积是20平方厘米。
第
3节
三角形的面积
【知识梳理】
三角形面积=底×高÷2
三角形底=面积×2÷高
三角形高=面积×2÷底
【诊断自测】
1、用字母表示下面各图形面积公式。?????
三角形:(????)?
平行四边形:(
)????梯形:(????)
2、三角形的面积是与它等底等高的平行四边形面积的
。
3、一个平行四边形的面积是18平方米,与它等底等高的三角形的面积是
4、计算下列三角形的面积。(单位:厘米)
(1)
(2)
【考点突破】
类型一:三角形面积公式的理解和应用
例1、一个三角形的高是4.1米,比底短0.5米,面积是(
)平方米。
答案:9.43
解析:
例2、一个三角形的面积是2.4平方分米,底是3分米,对应的高是(???
)。
答案:1.6dm
解析:
例3、一个等腰直角三角形,一条腰长3.5分米,这个三角形的面积是(
)平方分米。
答案:6.125
解析:直角三角形的两条直角边互为一组底和高,面积是直角边乘积的一半。
类型二:三角形面积相关解决问题
例4、一块长方形菜地,长60米,宽40米,在这块菜地中间有一个三角形水池,水池的底边长是16米,高是20米,这块菜地可以耕种的面积有多大?
答案:2240(平方米)
解析:
例5、一个梯形上底是5厘米,下底是8.2厘米,高是4.5厘米,如果在这个梯形中剪去一个最大的三角形,剩下的面积是多少平方厘米?
答案:11.25平方厘米
解析:画出图形,由题意可知,最大的三角形是以梯形下底的三角形,剩余部分是以梯形上底和高为底和高的三角形
S=
例6、一块三角形白菜地的面积是21.6平方米,它的底是5.4米,如果每棵白菜占地9平方分米,这块地一共有白菜(
)棵.
答案:240
解析:根据题目要求求解白菜的颗数。
(颗)
类型三:三角形面积与其他图形面积的关系
例7、下面梯形中两个阴影部分的面积相比,甲()乙。()应填(
)。
A.大于????B.小于????C.等于????D.无法确定
答案:C
解析:梯形的对角线将梯形分成的三角形,同底等高面积相等,减去重叠部分,得到甲乙面积相同。
类型四:三角形综合变形问题
例8、下图中正方形的边长为8厘米,CE为20厘米,梯形BCDF的面积是多少平方厘米?
答案:51.2平方厘米
解析:要求梯形的面积,关键是要求出上底FD的长度。连接FC后就能得到一个三角形EFC,用△EBC的面积减去△FBC的面积就能得到△EFC的面积:8×20÷2-8×8÷2=48(平方厘米)。FD=
48×2÷20=4.8(厘米)。所求梯形的面积就是
(4.8+8)×8÷2=51.2(平方厘米)。
答:梯形BCDF的面积是51.2平方厘米。
例9、右图是由八个边长是l厘米的小正方形拼成的长方形。求阴影部分的面积。
答案:5平方厘米
解析:阴影部分的面积是一个不能直接用公式求得的多边形,通过仔细观察可以发现,阴影部分的面积可以通过长方形的面积减去两个直角三角形的面积求得。阴影部分的面积=8×1-(3×1÷2)×2=5平方厘米
答:阴影部分的面积是5平方厘米。
例10、正方形ABCD的边长是8厘米,长方形DEFG的长DE是10厘米。问长方形的宽DG为多少厘米?
答案:6.4(厘米)
解析:求DG可以转化为求长方形的面积,题目已知正方形的边长和长方形的长的长度,可以得到正方形的面积,那如何利用正方形面积这个条件?观察发现正方形ABCD和长方形DEFG的重叠部分是一个多边形,这个多边形的面积无法求出,所以连结EC,既是正方形ABCD的一半,又是长方形EDGF的一半,就可以通过这个关系求出长方形的面积。
=8×8÷2=32(平方厘米)
=32×2=64(平方厘米)
DG=64÷10=6.4(厘米)
【易错精选】
下图阴影部分的面积是42平方分米,求梯形的面积。
2、判断:两个面积相等的三角形,底和高也相等.
(
)
3、一个三角形的底扩大2倍,高不变,它的面积扩大2倍。()
4、一个三角形和一个平行四边形的面积相等,底边也相等。已知平行四边形的高是6厘米,三角形的高是
(
)
A.3厘米
B.6厘米
C.12厘米
【精华提炼】
【总结】
1.三角形的面积等于它的底和该底上的高的积的一半。
2.同底(等底)同高(等高)的三角形面积相等,是与它等底等高的平行四边形面积的一半。
3.两个完全一样的三角形可以拼成一个平行四边形,两个完全一样的直角三角形可以拼成矩形和平行四边形,两个一样的等腰直角三角形可以拼成正方形和平行四边形。
【本节训练】
训练【1】一个三角形与一个平行四边形的面积和底都相等,平行四边形的高是3厘米,三角形的高是(
)厘米。
训练【2】求下图中阴影部分的面积。(单位:cm)
训练【3】求图中阴影部分的面积。(单位:厘米)
训练【4】在右图的梯形中剪下一个最大的三角形,剩下的图形是什么形状的?剩下的图形比剪下的图形小多少?
基础巩固
一、填空
1.
一个三角形的底是2.4米,高是27分米,同它等底等高的平行四边形面积是(
)平方分米。
2.
一个周长是92厘米的正方形,把它割补成一个平行四边形,它的面积是(
)。
3.
下图中的大正方形的边长是5厘米,小正方形的边长为4厘米,则阴影部分的面积为(
)平方厘米。
4.
一堆圆木,最底层有17根,最高层有5根,每相邻的两层间相差一根,这堆圆木共有(
)根。
5.
如下图是一个长方形,M是BC边中点,N是DC边中点,阴影部分占长方形面积的(
)。
一个三角形和一个平行四边形等底等高,这个三角形的面积是5.6平方米,平行四边形的面积是(
)平方米。
7.
三角形与平行四边形的面积相等,底也相等,平行四边形的高是5.8厘米,三角形的高是(
)分米。
8.
把一个边长是8分米的正方形拉成一个平行四边形,面积减少了4平方分米,这个平行四边形的高是(
)分米。
9.
两个完全相等的直角梯形正好拼成一个正方形,这个梯形的上底是8厘米,下底是12厘米,拼成后的正方形周长是(
)分米。
10.一个正方形的周长是20分米,它的面积与一个底是6.25分米的平行四边形的面积相等,这个平行四边形的高是(
)分米。
11.
用两个完全一样的梯形拼成一个面积是60平方厘米的平行四边形,如果梯形的上、下底之和是15厘米,高是(
)厘米。
12.
一个平行四边形分成一个三角形和一个梯形两部分(如图,单位:厘米)。已知它们的面积相差18.6平方厘米,则梯形的上底是(
)厘米。
13.一个周长是72厘米的正方形,把它割补成一个平行
四边形,它的面积是(
)平方厘米。
二、判断题
1.三角形的面积等于平行四边形面积的一半。
(
)
2.平行四边形的面积大于梯形面积。
(
)
3.任何一个梯形都可以分成两个等高的三角形。
(
)
4.两个面积相等的三角形一定能拼成一个平行四边形。
(
)
5.平行四边形的面积等于一个三角形面积的2倍。
(
)
6.
平行四边形的底是三角形的底的2倍,平行四边形的高是三角形的高的2倍,那么平行四边形的面积是三角形面积的4倍。
(
)
7.
梯形面积公式是“万能公式”。当上底和下底相等时,梯形公式就变成平行四边形公式;当上底为0时,又变成三角形公式;又因为平行四边形、长方形、正方形的特殊关系,因而又运用于长方形、正方形面积的计算。
(
)
8.
两个完全一样的直角梯形一定可以拼成一个(1)
平行四边形
(
)
(2)
长方形
(
)
(3)
等腰梯形
(
)
(4)
等腰三角形
(
)
(5)
直角梯形
(
)
三、计算面积
1.已知正方形ABCD的边长是7厘米,求正方形EFGH的面积。
2.有一个梯形,它的上底是5厘米,下底7厘米,如果只把上底增加3厘米,那么面积就增加4.5平方厘米。求原来梯形的面积。
3.如下图。已知大正方形的边长是12厘米,求中间最小正方形的面积。
巅峰突破
1.如图,正方形ABCD边长是6厘米,三角形AFD是正方形的一部分,三角形FCE的面积比三角形AFD大6平方厘米,求CE长多少厘米。
如图所示,三角形甲的面积与三角形乙的面积的关系是
A.大于??
B.小于??
C.等于
3、求下面组合图形的面积。(单位:cm)
如图,正方形ABCD
与正方形EFCH
的边长分别为3
和2
,若点B
、C
、F
在同一条直线上,点D
、C
、H
在同一条直线上,则三角形BDE
的面积为(????
)。
5、求图中四边形的面积。
参考答案
【诊断自测】
答案:1、;;
2、一半
3、9平方米
4、(1)4.2×2.5÷2=5.25(平方厘米)
(2)1.6×3.5÷2=2.8(平方厘米)
【本节训练】
1、6
2、8平方厘米
3、6厘米
4、解:从梯形的左下角到右上角剪下的三角形是最大的三角形,剩下的图形也是三角形;
25×12÷2﹣15×12÷2
=150﹣90
=60(平方厘米)
答:剩下的图形是三角形,剩下的图形比剪下的图形小60平方厘米.
【易错精选】
答案:1、60平方分米
2、错误
3、正确
4、C
基础巩固
一、填空
1.
648
2.
529平方厘米
提示:正方形与割补后的平行四边形的面积相同。
3.
8提示:两个正方形面积之和减去△ABC、△GBF、△CFE的面积。
4.
143
5.
6.
11.2
7.
1.16提示:三角形与平行四边形面积相等,底也相等,则三角形的高是平行四边形高的2倍。
8.
7.5提示:(8×8-4)÷8=7.5(分米)。
9.
8提示:(12+8)×4=80(厘米)=8(分米)。
10.
4提示:(分米)。
11.
4提示:60÷15=4(厘米),梯形上、下底之和即平行四边形的底。
12.
3提示:设梯形上底为,三角形的底为
=3。
13.
324提示:割补后正方形的面积与平行四边形面积相等。
二、判断
1.×
2.×
3.√
4.×
5.×
6.×
7.√
8.(1)
√
(2)
√
(3)√
(4)
×
(5)
×
三、计算面积
1.
7×7÷2=24.5(平方厘米)
2.
4.5×2÷3=3(厘米)
(5+7)×3÷2=18(平方厘米)
3.
12×12÷2÷2=36(平方厘米)
巅峰突破
1、解:设三角形AFD的面积为甲,三角形FCE的面积为乙,梯形ABCF的面积为丙。
乙=甲+6,丙+甲=6×6=36,可得
丙+乙=丙+甲+6=36+6=
42,即三角形ABE的面积等于42平方厘米。
BE=42×2÷6=14(厘米),CE=14-6=8(厘米)
C
4、答案:20平方厘米
解析:图中的这个多边形已知了两条边的长度和两个角度:90度和45度,要利用45度这个角度可以构造出以45度为内角的等腰直角三角形:通过切割或填补。
大等腰直角三角形的面积:7×7÷2=24.5(平方厘米)
小等腰直角三角形的面积:3×3÷2=4.5(平方厘米)
四边形的面积=24.5-4.5=20(平方厘米)
答:四边形的面积是20平方厘米。
