冀教版数学九年级上册25.4相似三角形的判定(一)课件 (共22张PPT)
文档属性
| 名称 | 冀教版数学九年级上册25.4相似三角形的判定(一)课件 (共22张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 922.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-20 20:07:06 | ||
图片预览


文档简介
(共22张PPT)
(图2)
E
B
C
D
A
B
C
A
D
E
(图1)
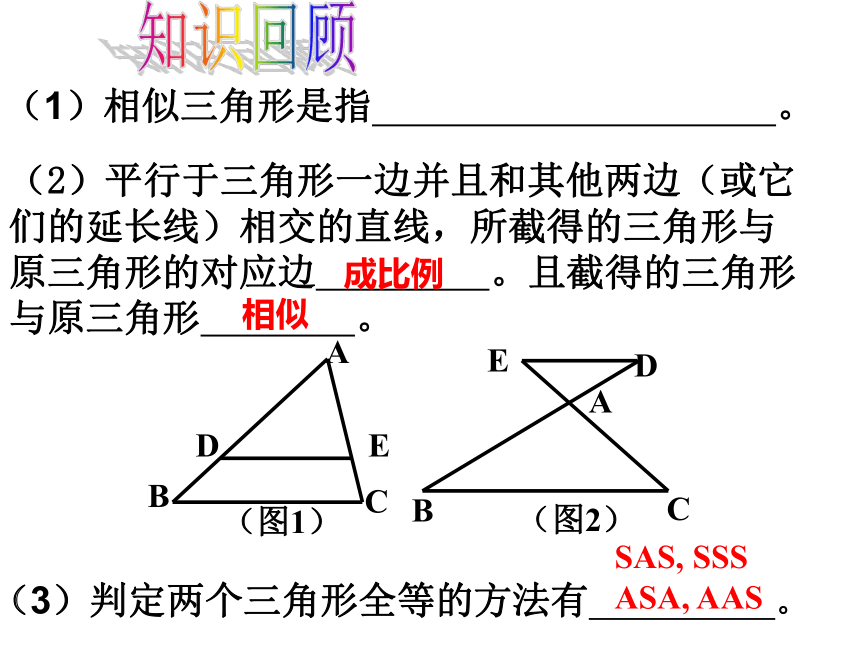
(3)判定两个三角形全等的方法有
。
(2)平行于三角形一边并且和其他两边(或它们的延长线)相交的直线,所截得的三角形与
原三角形的对应边
。且截得的三角形
与原三角形
。
(1)相似三角形是指
。
SAS,
SSS
ASA,
AAS
成比例
相似
45°
C
B
A
A′
C′
45°
B′
30°
C
B
A
30°
A′
C′
B′
图2
图1
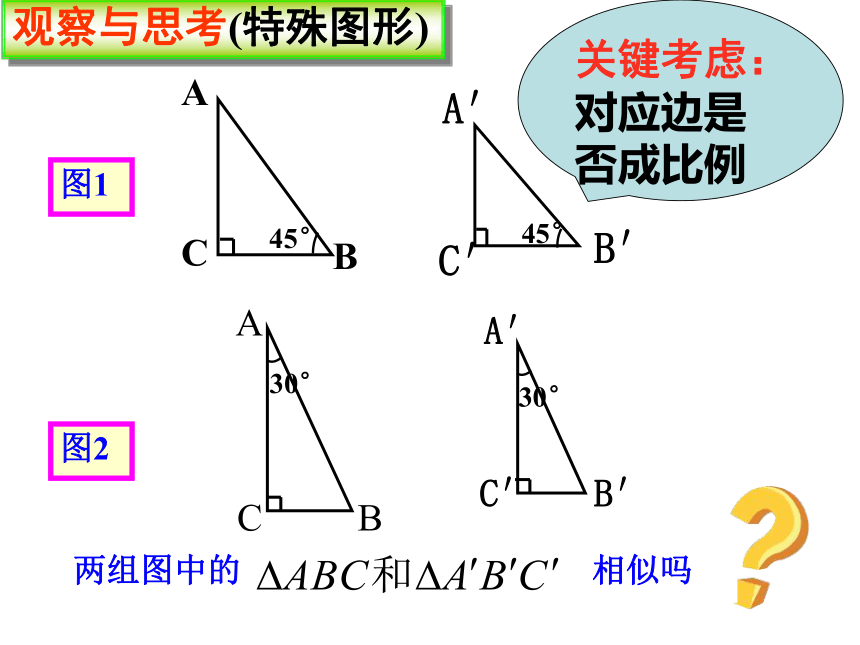
观察与思考(特殊图形)
两组图中的
相似吗
关键考虑:对应边是
否成比例
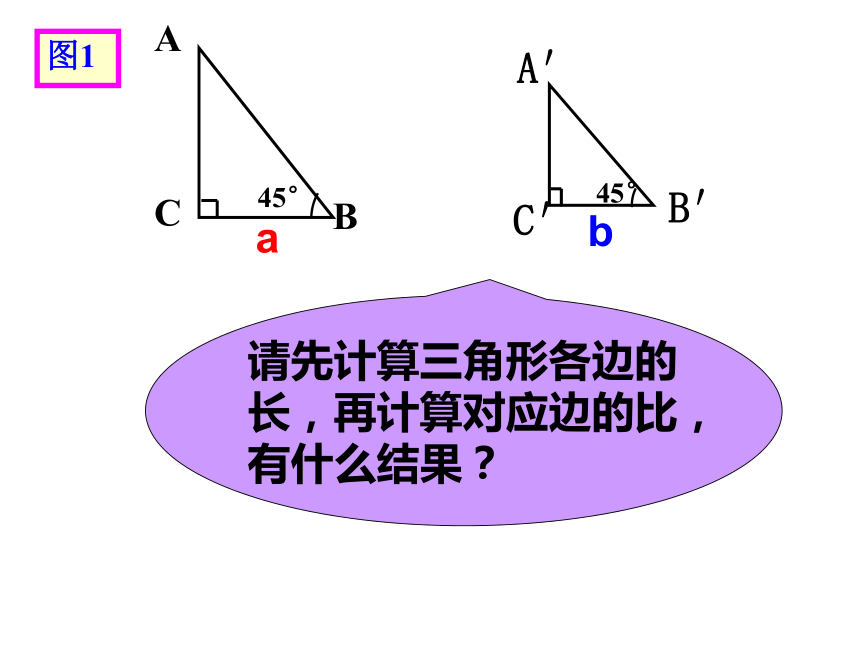
请先计算三角形各边的长,再计算对应边的比,有什么结果?
45°
C
B
A
A′
C′
45°
B′
a
b
图1
图2
又∵∠C=∠
C′∠A=∠
A′
∴∠B=∠
B′
30°
C
B
A
30°
A′
C′
B′
a
2b
2a
b
两角对应相等的两个直角三角形相似
=
=
∴
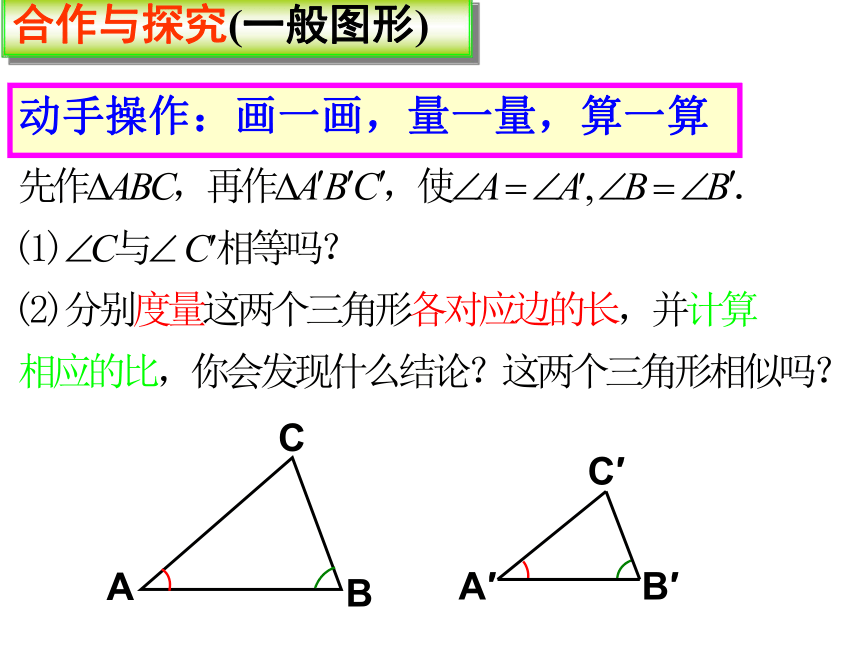
合作与探究(一般图形)
A
B
C
A′
B′
C′
动手操作:画一画,量一量,算一算
C
A
B
A′
B′
C
′
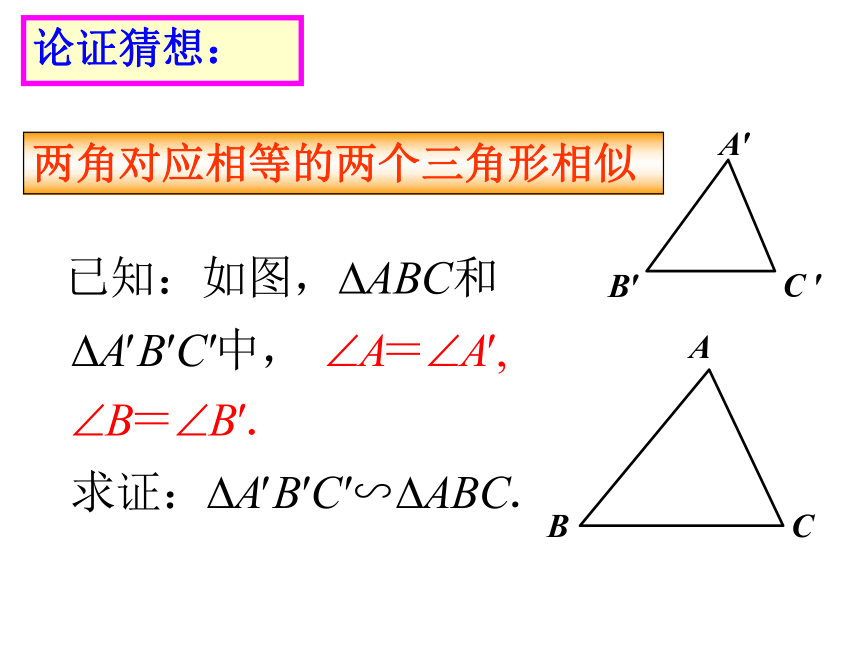
两角对应相等的两个三角形相似
论证猜想:
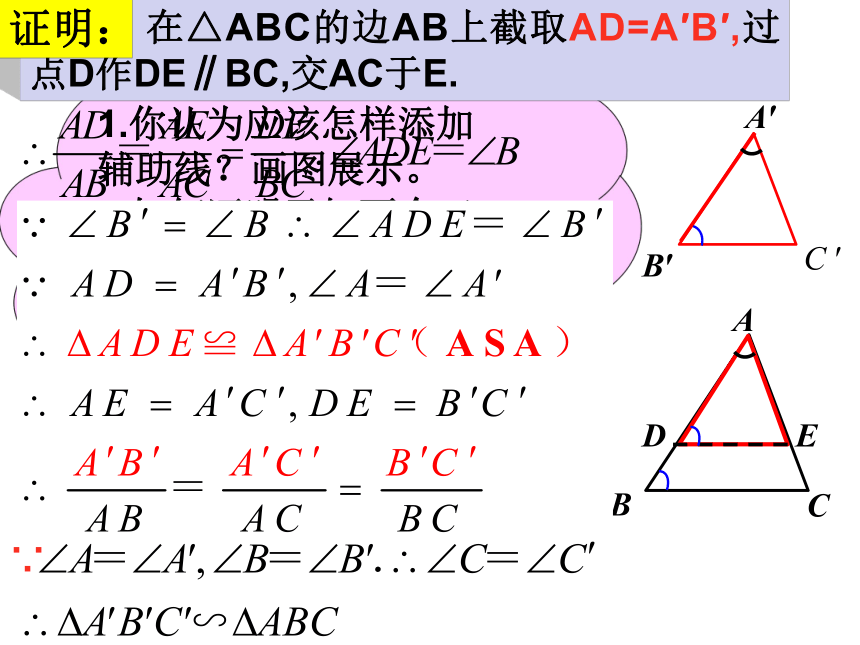
1.你认为应该怎样添加辅助线?画图展示。
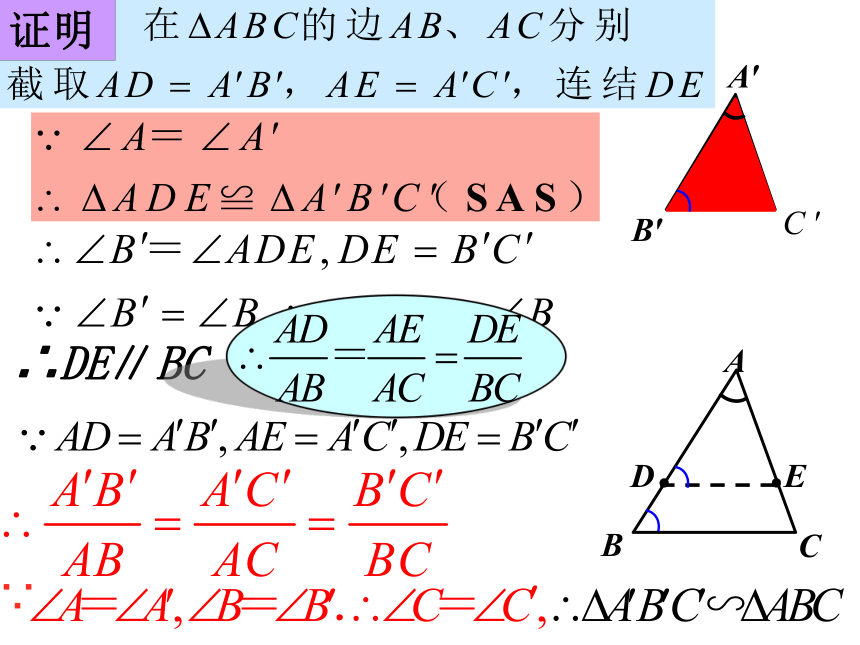
2.如何证明已知两个三角形的三边对应成比
例?进而得到三角形相似?
A
B
C
D
E
A′
B′
C
′
∵
在△ABC的边AB上截取AD=A′B′,过点D作DE∥BC,交AC于E.
证明:
A
B
C
A′
B′
C
′
∴DE∥BC
证明
∵
D
●
E
●
几何语言描述:
∵
A′
B′
C′
A
B
C
相似三角形判定定理1:
两角对应相等的两个三角形相似
B
C
A
E
D
证明
已知:如图在△ABC中,点D,E,F分别在边
AB,AC,BC上,且DE∥BC,
DF∥AC
求证:△ADE∽△DBF
E
D
C
B
A
F
想一想
1.已知条件含有平行线,能得到那些对应角相等?能找到两对对应角相等吗?
2.已知条件含有平行线,能否从预备定理证明?
相似三角形具有传递性
∥
∽
B
F
E
D
C
A
2
1
E
D
C
A
B
如图,AB⊥BD,
ED⊥BD,
C是线段BD的中点,AC⊥CE,
ED=1,BD=4,求AB的长。
证明:∵AC⊥CE
∴∠ACE=90°
∴∠1+∠2=90°
∵AB⊥BD
∴∠B=
90°
∴∠A+∠2=90°
∴∠A=∠1
∵ED⊥BD
∴∠B=∠D
∴△ABC∽
△CDE
1.本节课你学会了那些知识?
2.你哪方面的能力有所提高?
3.对你的师友想说些什么?
1.请将学案上所有题目的答案补充完整,做到查漏补缺。
2.完成课本第75页A组第1题和B组第2题。
3.预习相似三角形的判定二学案。
作业:
D
C
B
A
△ACD∽△ABC
△CBD∽△ABC
△CBD∽△ABC
△ACD∽△ABC∽
△CBD
D
C
B
A
3、已知:如图,点D在△ABC
的边AB上,
过点D作直线截△ABC,使截得的三角
形与原三角形相似你认为满足条件的
直线有几条?能把这些直线画出来吗?
2.要使△ACD∽△ABC,需添加的条件
是
。
D
C
B
A
E
C
B
D
A
第一种
B
C
D
A
G
第三种
C
D
B
A
F
第二种
A
C
B
D
H
第四种
请先计算三角形各边的长,再计算对应边的比,有什么结果?
45°
C
B
A
A′
C′
45°
B′
a
b
a
b
图1
=
=
∴
又∵∠C=∠
C′∠B=∠
B′
∴∠A=∠
A′
请先计算三角形各边的长,再计算对应边的比,有什么结果?
45°
C
B
A
A′
C′
45°
B′
a
b
图1
=
=
又∵∠C=∠
C′∠B=∠
B′
∴∠A=∠
A′
(图2)
E
B
C
D
A
B
C
A
D
E
(图1)
(3)判定两个三角形全等的方法有
。
(2)平行于三角形一边并且和其他两边(或它们的延长线)相交的直线,所截得的三角形与
原三角形的对应边
。且截得的三角形
与原三角形
。
(1)相似三角形是指
。
SAS,
SSS
ASA,
AAS
成比例
相似
45°
C
B
A
A′
C′
45°
B′
30°
C
B
A
30°
A′
C′
B′
图2
图1
观察与思考(特殊图形)
两组图中的
相似吗
关键考虑:对应边是
否成比例
请先计算三角形各边的长,再计算对应边的比,有什么结果?
45°
C
B
A
A′
C′
45°
B′
a
b
图1
图2
又∵∠C=∠
C′∠A=∠
A′
∴∠B=∠
B′
30°
C
B
A
30°
A′
C′
B′
a
2b
2a
b
两角对应相等的两个直角三角形相似
=
=
∴
合作与探究(一般图形)
A
B
C
A′
B′
C′
动手操作:画一画,量一量,算一算
C
A
B
A′
B′
C
′
两角对应相等的两个三角形相似
论证猜想:
1.你认为应该怎样添加辅助线?画图展示。
2.如何证明已知两个三角形的三边对应成比
例?进而得到三角形相似?
A
B
C
D
E
A′
B′
C
′
∵
在△ABC的边AB上截取AD=A′B′,过点D作DE∥BC,交AC于E.
证明:
A
B
C
A′
B′
C
′
∴DE∥BC
证明
∵
D
●
E
●
几何语言描述:
∵
A′
B′
C′
A
B
C
相似三角形判定定理1:
两角对应相等的两个三角形相似
B
C
A
E
D
证明
已知:如图在△ABC中,点D,E,F分别在边
AB,AC,BC上,且DE∥BC,
DF∥AC
求证:△ADE∽△DBF
E
D
C
B
A
F
想一想
1.已知条件含有平行线,能得到那些对应角相等?能找到两对对应角相等吗?
2.已知条件含有平行线,能否从预备定理证明?
相似三角形具有传递性
∥
∽
B
F
E
D
C
A
2
1
E
D
C
A
B
如图,AB⊥BD,
ED⊥BD,
C是线段BD的中点,AC⊥CE,
ED=1,BD=4,求AB的长。
证明:∵AC⊥CE
∴∠ACE=90°
∴∠1+∠2=90°
∵AB⊥BD
∴∠B=
90°
∴∠A+∠2=90°
∴∠A=∠1
∵ED⊥BD
∴∠B=∠D
∴△ABC∽
△CDE
1.本节课你学会了那些知识?
2.你哪方面的能力有所提高?
3.对你的师友想说些什么?
1.请将学案上所有题目的答案补充完整,做到查漏补缺。
2.完成课本第75页A组第1题和B组第2题。
3.预习相似三角形的判定二学案。
作业:
D
C
B
A
△ACD∽△ABC
△CBD∽△ABC
△CBD∽△ABC
△ACD∽△ABC∽
△CBD
D
C
B
A
3、已知:如图,点D在△ABC
的边AB上,
过点D作直线截△ABC,使截得的三角
形与原三角形相似你认为满足条件的
直线有几条?能把这些直线画出来吗?
2.要使△ACD∽△ABC,需添加的条件
是
。
D
C
B
A
E
C
B
D
A
第一种
B
C
D
A
G
第三种
C
D
B
A
F
第二种
A
C
B
D
H
第四种
请先计算三角形各边的长,再计算对应边的比,有什么结果?
45°
C
B
A
A′
C′
45°
B′
a
b
a
b
图1
=
=
∴
又∵∠C=∠
C′∠B=∠
B′
∴∠A=∠
A′
请先计算三角形各边的长,再计算对应边的比,有什么结果?
45°
C
B
A
A′
C′
45°
B′
a
b
图1
=
=
又∵∠C=∠
C′∠B=∠
B′
∴∠A=∠
A′
同课章节目录
- 第23章 数据分析
- 23.1 平均数与加权平均数
- 23.2 中位数与众数
- 23.3 方差
- 23.4 用样本估计总体
- 第24章 一元二次方程
- 24.1 一元二次方程
- 24.2 解一元二次方程
- 24.3 一元二次方程根与系数的关系
- 24.4 一元二次方程的应用
- 第25章 图形的相似
- 25.1 比例线段
- 25.2 平行线分线段成比例
- 25.3 相似三角形
- 25.4 相似三角形的判定
- 25.5 相似三角形的性质
- 25.6 相似三角形的应用
- 25.7 相似多边形和图形的位似
- 第26章 解直角三角形
- 26.1 锐角三角函数
- 26.2 锐角三角函数的计算
- 26.3 解直角三角形
- 26.4 解直角三角形的应用
- 第27章 反比例函数
- 27.1 反比例函数
- 27.2 反比例函数的图像和性质
- 27.3 反比例函数的应用
- 第28章 圆
- 28.1 圆的概念和性质
- 28.2 过三点的圆
- 28.3 圆心角和圆周角
- 28.4 垂径定理
- 28.5 弧长和扇形面积
