五年级上册数学表格式教案6.4组合图形的面积人教版
文档属性
| 名称 | 五年级上册数学表格式教案6.4组合图形的面积人教版 |
|
|
| 格式 | zip | ||
| 文件大小 | 60.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-20 09:39:11 | ||
图片预览


文档简介
教师姓名
单位名称
填写时间
2020/8/23
学科
数学
年级/册
五年级上册
教材版本
人教版
课题名称
第六单元
组合图形的面积
难点名称
组合图形的分解和整合
难点分析
从知识角度分析为什么难
本知识点是将学生所学的长方形、正方形、平行四边形、三角形、梯形面积计算进行整合,进行的一种由形象到抽象的学习,解题的基本理念是将组合图形转化为基本图形进行计算,需要发散学生的思维,会分析图形的构成,能够正确分析图形的隐含数据条件,注重将解决问题的思考策略渗透其中,提高学生的综合能力。
从学生角度分析为什么难
组合图形面积是由直观走向抽象的一节内容,重在方法的挖掘。学生空间思维能力较弱还处于初级阶段,只局限于对单一图形进行简单分析和面积计算,对于组合图形的面积还需要进一步认识和掌握,而本节课旨在提高学生综合实践能力,进一步发展学生的空间观念,是让学生在知识迁移、转化等数学思想方面及解决问题的策略方面有所发展。
难点教学方法
通过观察、拆分、运用推理迁移、转化的数学思想掌握组合图形的面积计算方法。
2、教师引导、自主探究,小组合作交流。
教学环节
教学过程
导入
复习学过的平面图形的面积计算公式。
揭示组合图形的定义。
3、引入新课。
知识讲解
(难点突破)
1、出示小明家地板平面图(PPT展示)
最近小明家搬了新家,需要铺木地板,请大家帮他算一算他家至少要买多少平米的木地板?
如何准确的计算出小明家的地板有多大面积?(将复杂的图形转化成基本图形)
2、请同学们试算。
3、展示学生的算法。
预设1:可以分成一个大长方形和小长方形。最后算出它们的面积和,就可以求出这个图形的面积。
算式:(6-3)×4+7×3=33(m?)
预设2:可以分成一个正方形和一个长方形。最后两个面积相加得到组合图形的面积。
算式:(6-3)×3+4×6=33(m?)
预设3:可以分成两个梯形相加得到组合图形的面积。
算式:7-4=3(m)(3+7)×3÷2=15(m?)
6-3=3(m)(3+6)×4÷2=18(m?)
15+18=33(m?)
师:这些都是将组合图形分隔成几个简单图形的方法,还有其他同学有不同的方法吗?
预设4:把这个组合图形“补成”一个大的长方形,最后再减去补的那一部分。
算式:7×6-(6-3)×(7-4)=33(m?)
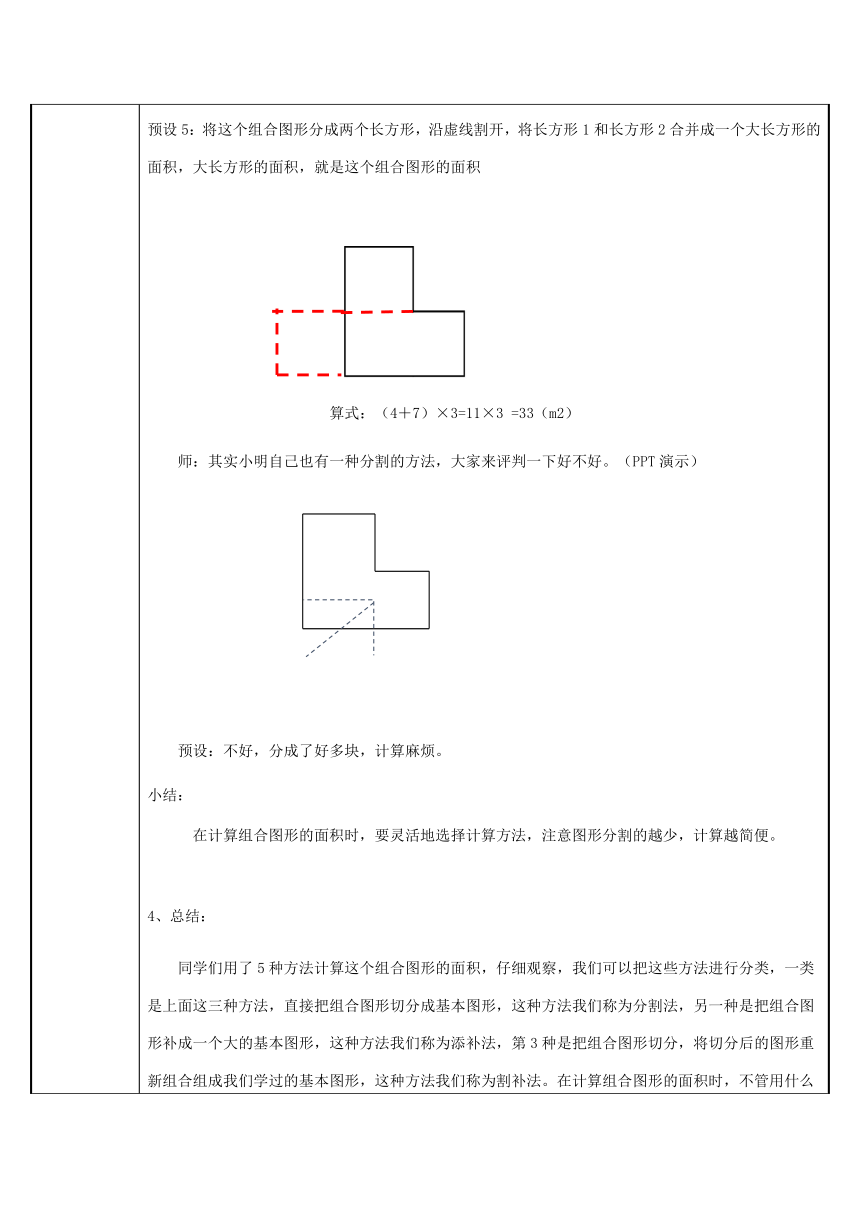
预设5:将这个组合图形分成两个长方形,沿虚线割开,将长方形1和长方形2合并成一个大长方形的面积,大长方形的面积,就是这个组合图形的面积
算式:(4+7)×3=11×3
=33(m2)
师:其实小明自己也有一种分割的方法,大家来评判一下好不好。(PPT演示)
预设:不好,分成了好多块,计算麻烦。
小结:
在计算组合图形的面积时,要灵活地选择计算方法,注意图形分割的越少,计算越简便。
4、总结:
同学们用了5种方法计算这个组合图形的面积,仔细观察,我们可以把这些方法进行分类,一类是上面这三种方法,直接把组合图形切分成基本图形,这种方法我们称为分割法,另一种是把组合图形补成一个大的基本图形,这种方法我们称为添补法,第3种是把组合图形切分,将切分后的图形重新组合组成我们学过的基本图形,这种方法我们称为割补法。在计算组合图形的面积时,不管用什么方法,都是将组合图形转化为基本图形来计算
课堂练习
(难点巩固)
灵活应用,巩固新知
出示教材第99页例4:师:刚才同学们帮小明算了客厅的面积,下图是房子侧面墙的形状?你能算出它的面积吗?你能想出几种方法?小组合作,讨论完成。(PPT展示)
预设1:用分割法把这个组合图形一分为二,一个是正方形,另一个是三角再分别算出正方形和三角形的面积,最后算出它们的面积和,就可以求出这个图形的面积。(PPT出示第一种方法)
5×5=25(m?)5×2÷2=5(m?)
25+5=30(m?)
预设2:用分割法,把这个图形分成两个梯形,这两个梯形面积是相等的,所以只要求出一个梯形的面积再乘以2,就得到这个组合图形的面积。(PPT出示第二种方法)
(5+7)×2.5÷2×2=30(m?)
预设3:用割补法先把这个图形补上两个三角形,看作一个长方形,先算出长方的面积后,再减去两个小三角形的面积。(PPT出示第三种方法)
5×(5+2)-2.5×2÷2×2=30(m?)
小结
这节课你有什么收获?
引导总结:
首先要确立转化思想,将组合图形,利用分割法、添补法,割补法转化为基本图形,总之我们在见到组合图形时,就要利用转化思想
尝试用学过的知识解决新问题,把复杂的问题分解成几个简单的问题逐一解决。
单位名称
填写时间
2020/8/23
学科
数学
年级/册
五年级上册
教材版本
人教版
课题名称
第六单元
组合图形的面积
难点名称
组合图形的分解和整合
难点分析
从知识角度分析为什么难
本知识点是将学生所学的长方形、正方形、平行四边形、三角形、梯形面积计算进行整合,进行的一种由形象到抽象的学习,解题的基本理念是将组合图形转化为基本图形进行计算,需要发散学生的思维,会分析图形的构成,能够正确分析图形的隐含数据条件,注重将解决问题的思考策略渗透其中,提高学生的综合能力。
从学生角度分析为什么难
组合图形面积是由直观走向抽象的一节内容,重在方法的挖掘。学生空间思维能力较弱还处于初级阶段,只局限于对单一图形进行简单分析和面积计算,对于组合图形的面积还需要进一步认识和掌握,而本节课旨在提高学生综合实践能力,进一步发展学生的空间观念,是让学生在知识迁移、转化等数学思想方面及解决问题的策略方面有所发展。
难点教学方法
通过观察、拆分、运用推理迁移、转化的数学思想掌握组合图形的面积计算方法。
2、教师引导、自主探究,小组合作交流。
教学环节
教学过程
导入
复习学过的平面图形的面积计算公式。
揭示组合图形的定义。
3、引入新课。
知识讲解
(难点突破)
1、出示小明家地板平面图(PPT展示)
最近小明家搬了新家,需要铺木地板,请大家帮他算一算他家至少要买多少平米的木地板?
如何准确的计算出小明家的地板有多大面积?(将复杂的图形转化成基本图形)
2、请同学们试算。
3、展示学生的算法。
预设1:可以分成一个大长方形和小长方形。最后算出它们的面积和,就可以求出这个图形的面积。
算式:(6-3)×4+7×3=33(m?)
预设2:可以分成一个正方形和一个长方形。最后两个面积相加得到组合图形的面积。
算式:(6-3)×3+4×6=33(m?)
预设3:可以分成两个梯形相加得到组合图形的面积。
算式:7-4=3(m)(3+7)×3÷2=15(m?)
6-3=3(m)(3+6)×4÷2=18(m?)
15+18=33(m?)
师:这些都是将组合图形分隔成几个简单图形的方法,还有其他同学有不同的方法吗?
预设4:把这个组合图形“补成”一个大的长方形,最后再减去补的那一部分。
算式:7×6-(6-3)×(7-4)=33(m?)
预设5:将这个组合图形分成两个长方形,沿虚线割开,将长方形1和长方形2合并成一个大长方形的面积,大长方形的面积,就是这个组合图形的面积
算式:(4+7)×3=11×3
=33(m2)
师:其实小明自己也有一种分割的方法,大家来评判一下好不好。(PPT演示)
预设:不好,分成了好多块,计算麻烦。
小结:
在计算组合图形的面积时,要灵活地选择计算方法,注意图形分割的越少,计算越简便。
4、总结:
同学们用了5种方法计算这个组合图形的面积,仔细观察,我们可以把这些方法进行分类,一类是上面这三种方法,直接把组合图形切分成基本图形,这种方法我们称为分割法,另一种是把组合图形补成一个大的基本图形,这种方法我们称为添补法,第3种是把组合图形切分,将切分后的图形重新组合组成我们学过的基本图形,这种方法我们称为割补法。在计算组合图形的面积时,不管用什么方法,都是将组合图形转化为基本图形来计算
课堂练习
(难点巩固)
灵活应用,巩固新知
出示教材第99页例4:师:刚才同学们帮小明算了客厅的面积,下图是房子侧面墙的形状?你能算出它的面积吗?你能想出几种方法?小组合作,讨论完成。(PPT展示)
预设1:用分割法把这个组合图形一分为二,一个是正方形,另一个是三角再分别算出正方形和三角形的面积,最后算出它们的面积和,就可以求出这个图形的面积。(PPT出示第一种方法)
5×5=25(m?)5×2÷2=5(m?)
25+5=30(m?)
预设2:用分割法,把这个图形分成两个梯形,这两个梯形面积是相等的,所以只要求出一个梯形的面积再乘以2,就得到这个组合图形的面积。(PPT出示第二种方法)
(5+7)×2.5÷2×2=30(m?)
预设3:用割补法先把这个图形补上两个三角形,看作一个长方形,先算出长方的面积后,再减去两个小三角形的面积。(PPT出示第三种方法)
5×(5+2)-2.5×2÷2×2=30(m?)
小结
这节课你有什么收获?
引导总结:
首先要确立转化思想,将组合图形,利用分割法、添补法,割补法转化为基本图形,总之我们在见到组合图形时,就要利用转化思想
尝试用学过的知识解决新问题,把复杂的问题分解成几个简单的问题逐一解决。
