25.5相似三角形法的性质 冀教版数学九年级上册 课件2(共25张PPT)
文档属性
| 名称 | 25.5相似三角形法的性质 冀教版数学九年级上册 课件2(共25张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-21 07:47:03 | ||
图片预览



文档简介
(共25张PPT)
25.5相似三角形的性质
相似三角形的识别
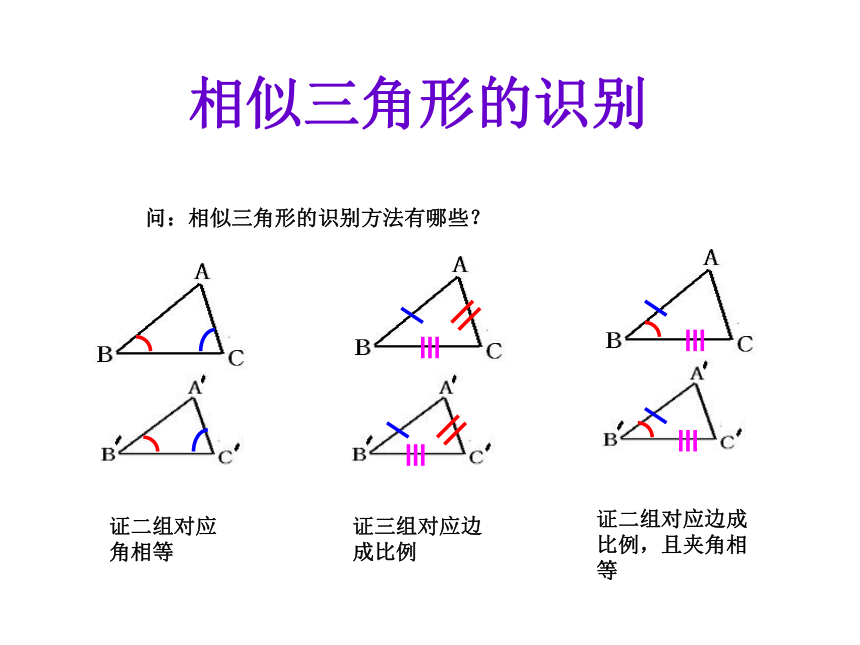
问:相似三角形的识别方法有哪些?
证二组对应角相等
证三组对应边成比例
证二组对应边成比例,且夹角相等
相似三角形的特征
问:你知道相似三角形的特征是什么吗?
角:对应角相等
边:对应边成比例
问:什么是相似比?
相似比=对应边的比值=
如右图,△A
B
C
∽△A′B′C′
A
B
C
A’
B’
C’
D
D’
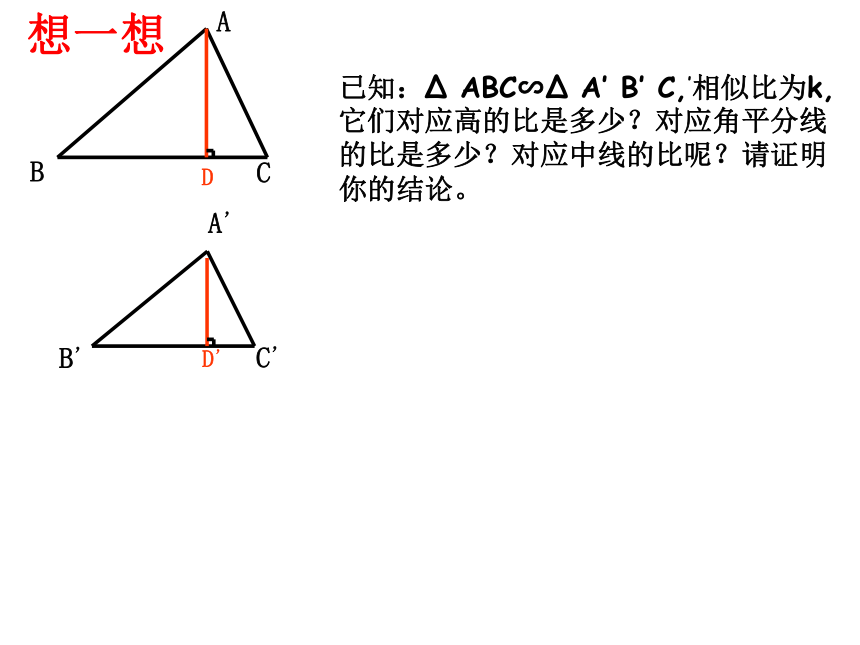
已知:Δ
ABC∽Δ
A’
B’
C,’相似比为k,它们对应高的比是多少?对应角平分线的比是多少?对应中线的比呢?请证明你的结论。
想一想
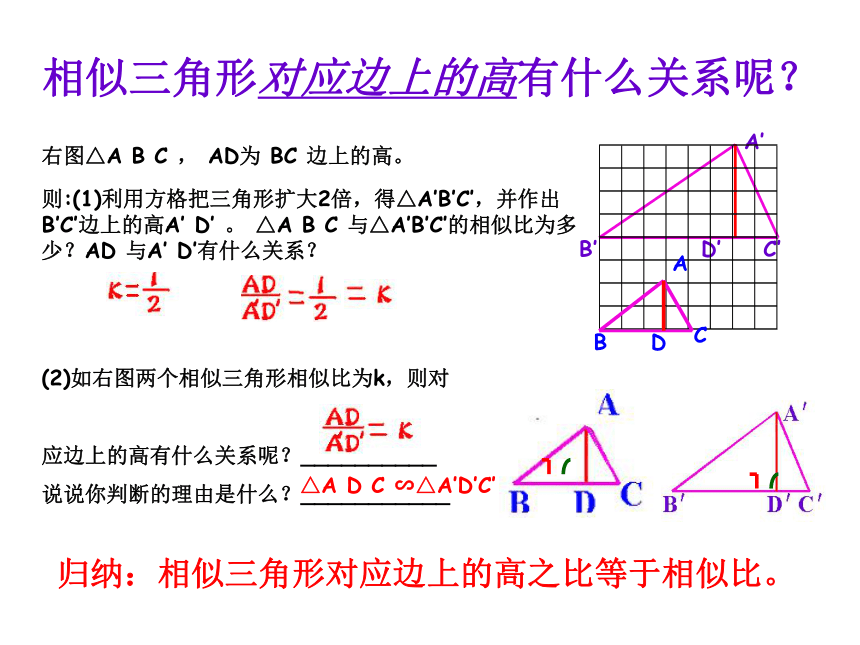
相似三角形对应边上的高有什么关系呢?
归纳:相似三角形对应边上的高之比等于相似比。
A′
B′
C′
D′
△A
D
C
∽△A′D′C′
则:(1)利用方格把三角形扩大2倍,得△A′B′C′,并作出B′C′边上的高A′
D′
。
△A
B
C
与△A′B′C′的相似比为多少?AD
与A′
D′有什么关系?
右图△A
B
C
,
AD为
BC
边上的高。
D
A
B
C
(2)如右图两个相似三角形相似比为k,则对
应边上的高有什么关系呢?__________
说说你判断的理由是什么?___________
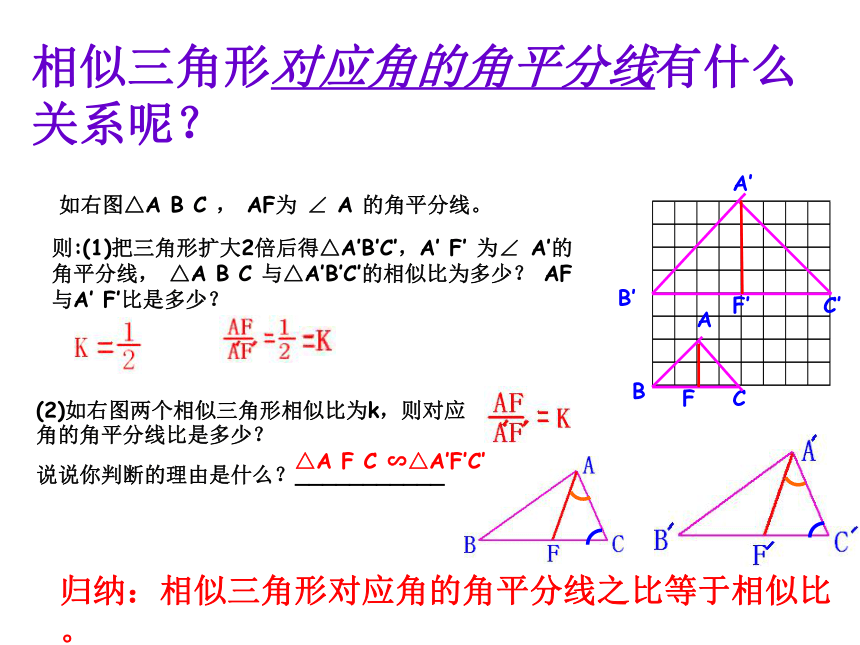
相似三角形对应角的角平分线有什么关系呢?
归纳:相似三角形对应角的角平分线之比等于相似比。
(2)如右图两个相似三角形相似比为k,则对应角的角平分线比是多少?
说说你判断的理由是什么?___________
△A
F
C
∽△A′F′C′
如右图△A
B
C
,
AF为
∠
A
的角平分线。
则:(1)把三角形扩大2倍后得△A′B′C′,A′
F′
为∠
A′的角平分线,
△A
B
C
与△A′B′C′的相似比为多少?
AF
与A′
F′比是多少?
A
B
C
F
A′
B′
C′
F′
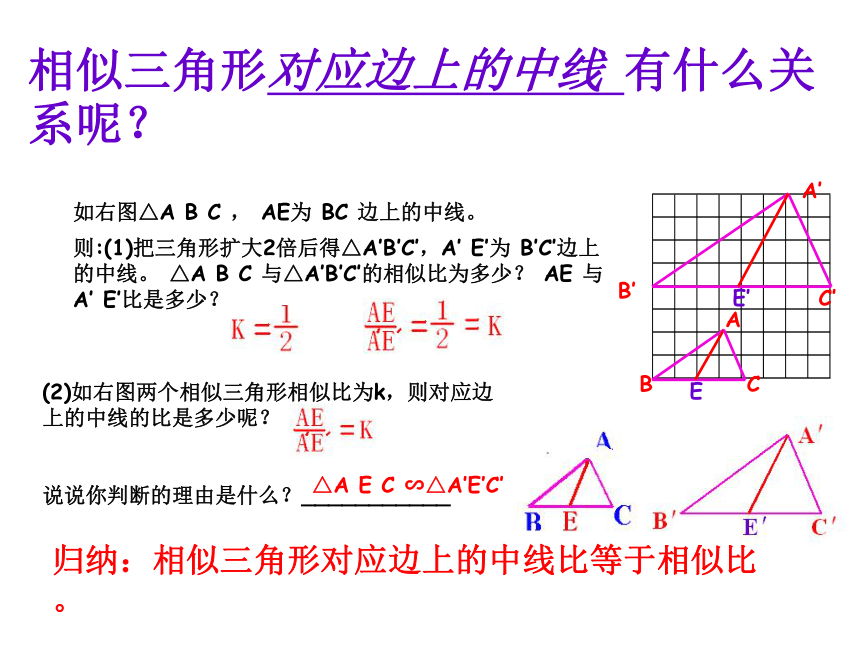
归纳:相似三角形对应边上的中线比等于相似比。
相似三角形对应边上的中线
有什么关系呢?
如右图△A
B
C
,
AE为
BC
边上的中线。
则:(1)把三角形扩大2倍后得△A′B′C′,A′
E′为
B′C′边上的中线。
△A
B
C
与△A′B′C′的相似比为多少?
AE
与A′
E′比是多少?
A
B
C
E
A′
B′
C′
E′
△A
E
C
∽△A′E′C′
(2)如右图两个相似三角形相似比为k,则对应边上的中线的比是多少呢?
说说你判断的理由是什么?___________
课堂练习:
填空:
(1)两个三角形的对应边的比为3:4,则这两个三角形的对应角平分线的比为_____
,对应边上的高的比为____,对应边上的中线的比为____
(2)相似三角形对应角平分线比为0.2,则相似比为_________,对应中线的比等于______;
相似三角形对应高的比,对应中线的比、对应角平分线的比都等于相似比.
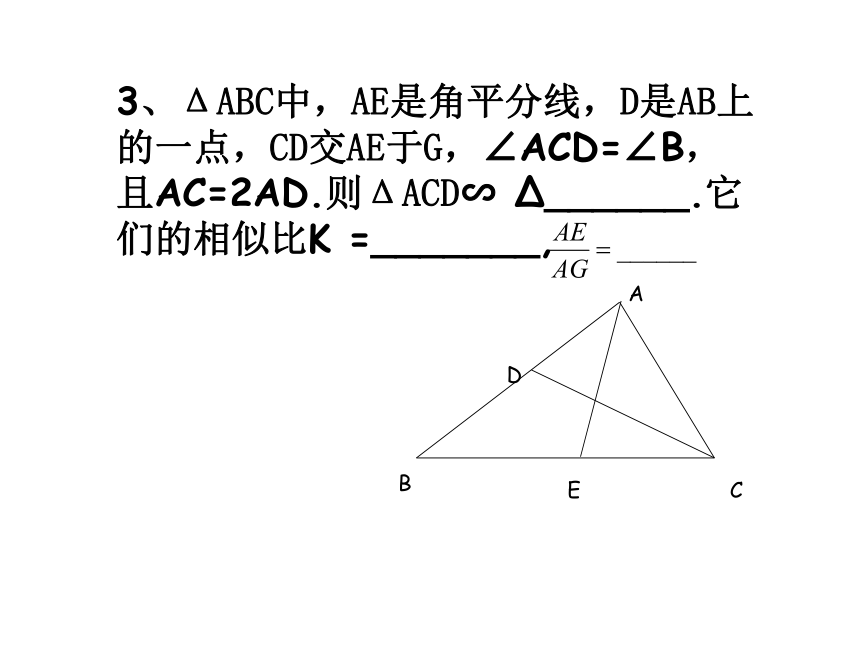
3、ΔABC中,AE是角平分线,D是AB上的一点,CD交AE于G,∠ACD=∠B,且AC=2AD.则ΔACD∽
Δ______.它们的相似比K
=_______,
A
B
C
E
D
S
B
C
R
E
D
A
例1,如图,
AD是△ABC的高AD=h,点R在AC边上,SR⊥AD垂足为
E,当SR=
BC时,求DE的长。如果SR=
BC呢?
解:
∵SR⊥AD
BC⊥AD
∴
即
∴
∴SR//BC
∴∠ASR=∠B,∠ARS=∠C
Δ
ASR∽Δ
ABC
当SR=
BC时
当SR=
BC时
1.已知△ABC∽△A′B′C′,BD和B′D′是它们的对应中线,
求BD的长?
小试牛刀
2、△ABC∽△A′B′C′,AD和
A′D′是它们的对应角平分线,已知AD=8cm,A′D′=3cm,求△ABC和△A′B′C′对应高的比.
你会应用吗?
3、△ABC∽△A′B′C′,BD和B′D′是它们的对应中线,已知
,B′D′=4cm,求BD的长.
解:∵
△ABC∽△A′B′C′,
BD和B′D′是它们的对应中线
∴
(相似三角形对应中线的比都等于相似比)
∴
BD=6
∴
4.如图是一个照相机成像的示意图,如果底片XY宽35mm,焦距是50mm,能拍摄5m外的景物有多宽?
拓广应用空间:
35mm
50mm
5m
X
Y
A
B
L
相似三角形的周长有什么关系呢?
归纳:相似三角形的周长比等于相似比。
右图(1)(2)(3)分别是边长为1、2、3的等边三角形,它们都相似.
(2)与(1)的相似比=________________,
(2)与(1)的周长比=________________;
(3)与(1)的相似比=________________,
(3)与(1)的周长比=________________.
2:1
2:1
3:1
3:1
从上面可以看出当相似比=k时,周长比=______
k
相似三角形的面积有什么关系呢?
2:1
归纳:相似三角形的面积比等于相似比的平方。
右图(1)(2)(3)分别是边长为1、2、3的等边三角形,它们都相似.
(2)与(1)的相似比=________________,
(2)与(1)的面积比=________________;
(3)与(1)的相似比=________________,
(3)与(1)的面积比=________________.
4:1
3:1
9:1
从上面可以看出当相似比=k时,面积比=______
k2
算一算:
ΔABC与ΔA’B’C’的相似比是
多少?
ΔABC与ΔA’B’C’的周长比是多少?
面积比是多少?
4×4正方形网格
看一看:
ΔABC与ΔA’B’C’有什么关系?
为什么?
想一想:
你发现上面两个相似三角形的周长比与相似比
有什么关系?面积比与相似比又有什么关系?
(相似)
√2
2
√2
周长比等于相似比,面积比等于相似比的平方
√10
2
√2
1
√5
√2
A
B
C
A’
C’
B’
已知两个三角形相似,请完成下列表格
相似比
周长比
面积比
注:周长比等于相似比,已知相似比或周长比,
求面积比要平方,
而已知面积比,求相似比或周长比则要开方。
2
4
100
100
10000
1
9
1
3
1
3
2
...
...
...
D
B
C
例2:如图将Δ
ABC沿BC方向平移得到△DEF。△ABC与△DEF重叠部分(图中阴影部分)的面积是△ABC面积的一半已知BC=2,求△ABC平移的距离。
A
E
F
△GEC∽△
ABC
解:根据题意,EG//AB
∠GEC=∠B,∠EGC=∠A
G
∴
∴
∴
即△ABC平移的距离为2-
B
A
C
D
E
如图,已知DE//BC,AB=30m,BD=18m,
ΔABC的周长为80m,面积为100m2,
求ΔADE的周长和面积
30m
18m
1、在△ABC中,DE??BC,E、D分别在AC、AB上,EC=2AE,则S
△ADE:S
△ABC的比为______
练习
2、如图,
△ABC中,DE??FG??BC,AD=DF=FB,则
S△ADE:S四边形DFGE:S四边形FBCG=____
A
B
C
D
E
S
△ADE:S四边形DBCE的比为______
1/9
1/8
1、把
一个三角形变成和它相似的三角形,则如果边长扩大为原来的100倍,那么面积扩大为原来的_____________倍;
如果面积扩大为原来的100倍,那么边长扩大为原来的_______________倍。
课堂练习
10000
10
2、已知△ABC∽△A′B′C′,AC:
A′
C′=4:3。
(1)若△ABC的周长为24cm,则△A′B′C′的周长为
cm;
(2)若△ABC的面积为32
cm2
,则△A′B′C′的面积为
cm2。
18
18
课堂练习
3、已知,在△A
B
C
中,DE||BC,
DE:BC=3:5
则(1)AD:DB=
(2)△ADE的面积:梯形DECB的面积=
(3)△A
B
C的面积为25,则△A
DE的面积=___
。
3:2
9:16
9
4、如图,已知DE∥BC,BD=3AD,S△ABC
=48,求:△ADE的面积。
课堂练习
解:因为DE∥BC
所以∠ADE=∠ABC,
∠AED=∠ACB
所以△A
DE
∽△ABC
又因为BD=3AD
可得相似比k=AD:AB=1:2
所以S△ADE
=1/4
S△ABC
=12
小结
相似三角形的性质
对应角相等、对应边成比例
对应高之比、对应中线之比、对应角平分线之比都等于相似比
周长之比等于相似比
面积之比等于相似比的平方
(你学到了什么呢?)
谢谢!
25.5相似三角形的性质
相似三角形的识别
问:相似三角形的识别方法有哪些?
证二组对应角相等
证三组对应边成比例
证二组对应边成比例,且夹角相等
相似三角形的特征
问:你知道相似三角形的特征是什么吗?
角:对应角相等
边:对应边成比例
问:什么是相似比?
相似比=对应边的比值=
如右图,△A
B
C
∽△A′B′C′
A
B
C
A’
B’
C’
D
D’
已知:Δ
ABC∽Δ
A’
B’
C,’相似比为k,它们对应高的比是多少?对应角平分线的比是多少?对应中线的比呢?请证明你的结论。
想一想
相似三角形对应边上的高有什么关系呢?
归纳:相似三角形对应边上的高之比等于相似比。
A′
B′
C′
D′
△A
D
C
∽△A′D′C′
则:(1)利用方格把三角形扩大2倍,得△A′B′C′,并作出B′C′边上的高A′
D′
。
△A
B
C
与△A′B′C′的相似比为多少?AD
与A′
D′有什么关系?
右图△A
B
C
,
AD为
BC
边上的高。
D
A
B
C
(2)如右图两个相似三角形相似比为k,则对
应边上的高有什么关系呢?__________
说说你判断的理由是什么?___________
相似三角形对应角的角平分线有什么关系呢?
归纳:相似三角形对应角的角平分线之比等于相似比。
(2)如右图两个相似三角形相似比为k,则对应角的角平分线比是多少?
说说你判断的理由是什么?___________
△A
F
C
∽△A′F′C′
如右图△A
B
C
,
AF为
∠
A
的角平分线。
则:(1)把三角形扩大2倍后得△A′B′C′,A′
F′
为∠
A′的角平分线,
△A
B
C
与△A′B′C′的相似比为多少?
AF
与A′
F′比是多少?
A
B
C
F
A′
B′
C′
F′
归纳:相似三角形对应边上的中线比等于相似比。
相似三角形对应边上的中线
有什么关系呢?
如右图△A
B
C
,
AE为
BC
边上的中线。
则:(1)把三角形扩大2倍后得△A′B′C′,A′
E′为
B′C′边上的中线。
△A
B
C
与△A′B′C′的相似比为多少?
AE
与A′
E′比是多少?
A
B
C
E
A′
B′
C′
E′
△A
E
C
∽△A′E′C′
(2)如右图两个相似三角形相似比为k,则对应边上的中线的比是多少呢?
说说你判断的理由是什么?___________
课堂练习:
填空:
(1)两个三角形的对应边的比为3:4,则这两个三角形的对应角平分线的比为_____
,对应边上的高的比为____,对应边上的中线的比为____
(2)相似三角形对应角平分线比为0.2,则相似比为_________,对应中线的比等于______;
相似三角形对应高的比,对应中线的比、对应角平分线的比都等于相似比.
3、ΔABC中,AE是角平分线,D是AB上的一点,CD交AE于G,∠ACD=∠B,且AC=2AD.则ΔACD∽
Δ______.它们的相似比K
=_______,
A
B
C
E
D
S
B
C
R
E
D
A
例1,如图,
AD是△ABC的高AD=h,点R在AC边上,SR⊥AD垂足为
E,当SR=
BC时,求DE的长。如果SR=
BC呢?
解:
∵SR⊥AD
BC⊥AD
∴
即
∴
∴SR//BC
∴∠ASR=∠B,∠ARS=∠C
Δ
ASR∽Δ
ABC
当SR=
BC时
当SR=
BC时
1.已知△ABC∽△A′B′C′,BD和B′D′是它们的对应中线,
求BD的长?
小试牛刀
2、△ABC∽△A′B′C′,AD和
A′D′是它们的对应角平分线,已知AD=8cm,A′D′=3cm,求△ABC和△A′B′C′对应高的比.
你会应用吗?
3、△ABC∽△A′B′C′,BD和B′D′是它们的对应中线,已知
,B′D′=4cm,求BD的长.
解:∵
△ABC∽△A′B′C′,
BD和B′D′是它们的对应中线
∴
(相似三角形对应中线的比都等于相似比)
∴
BD=6
∴
4.如图是一个照相机成像的示意图,如果底片XY宽35mm,焦距是50mm,能拍摄5m外的景物有多宽?
拓广应用空间:
35mm
50mm
5m
X
Y
A
B
L
相似三角形的周长有什么关系呢?
归纳:相似三角形的周长比等于相似比。
右图(1)(2)(3)分别是边长为1、2、3的等边三角形,它们都相似.
(2)与(1)的相似比=________________,
(2)与(1)的周长比=________________;
(3)与(1)的相似比=________________,
(3)与(1)的周长比=________________.
2:1
2:1
3:1
3:1
从上面可以看出当相似比=k时,周长比=______
k
相似三角形的面积有什么关系呢?
2:1
归纳:相似三角形的面积比等于相似比的平方。
右图(1)(2)(3)分别是边长为1、2、3的等边三角形,它们都相似.
(2)与(1)的相似比=________________,
(2)与(1)的面积比=________________;
(3)与(1)的相似比=________________,
(3)与(1)的面积比=________________.
4:1
3:1
9:1
从上面可以看出当相似比=k时,面积比=______
k2
算一算:
ΔABC与ΔA’B’C’的相似比是
多少?
ΔABC与ΔA’B’C’的周长比是多少?
面积比是多少?
4×4正方形网格
看一看:
ΔABC与ΔA’B’C’有什么关系?
为什么?
想一想:
你发现上面两个相似三角形的周长比与相似比
有什么关系?面积比与相似比又有什么关系?
(相似)
√2
2
√2
周长比等于相似比,面积比等于相似比的平方
√10
2
√2
1
√5
√2
A
B
C
A’
C’
B’
已知两个三角形相似,请完成下列表格
相似比
周长比
面积比
注:周长比等于相似比,已知相似比或周长比,
求面积比要平方,
而已知面积比,求相似比或周长比则要开方。
2
4
100
100
10000
1
9
1
3
1
3
2
...
...
...
D
B
C
例2:如图将Δ
ABC沿BC方向平移得到△DEF。△ABC与△DEF重叠部分(图中阴影部分)的面积是△ABC面积的一半已知BC=2,求△ABC平移的距离。
A
E
F
△GEC∽△
ABC
解:根据题意,EG//AB
∠GEC=∠B,∠EGC=∠A
G
∴
∴
∴
即△ABC平移的距离为2-
B
A
C
D
E
如图,已知DE//BC,AB=30m,BD=18m,
ΔABC的周长为80m,面积为100m2,
求ΔADE的周长和面积
30m
18m
1、在△ABC中,DE??BC,E、D分别在AC、AB上,EC=2AE,则S
△ADE:S
△ABC的比为______
练习
2、如图,
△ABC中,DE??FG??BC,AD=DF=FB,则
S△ADE:S四边形DFGE:S四边形FBCG=____
A
B
C
D
E
S
△ADE:S四边形DBCE的比为______
1/9
1/8
1、把
一个三角形变成和它相似的三角形,则如果边长扩大为原来的100倍,那么面积扩大为原来的_____________倍;
如果面积扩大为原来的100倍,那么边长扩大为原来的_______________倍。
课堂练习
10000
10
2、已知△ABC∽△A′B′C′,AC:
A′
C′=4:3。
(1)若△ABC的周长为24cm,则△A′B′C′的周长为
cm;
(2)若△ABC的面积为32
cm2
,则△A′B′C′的面积为
cm2。
18
18
课堂练习
3、已知,在△A
B
C
中,DE||BC,
DE:BC=3:5
则(1)AD:DB=
(2)△ADE的面积:梯形DECB的面积=
(3)△A
B
C的面积为25,则△A
DE的面积=___
。
3:2
9:16
9
4、如图,已知DE∥BC,BD=3AD,S△ABC
=48,求:△ADE的面积。
课堂练习
解:因为DE∥BC
所以∠ADE=∠ABC,
∠AED=∠ACB
所以△A
DE
∽△ABC
又因为BD=3AD
可得相似比k=AD:AB=1:2
所以S△ADE
=1/4
S△ABC
=12
小结
相似三角形的性质
对应角相等、对应边成比例
对应高之比、对应中线之比、对应角平分线之比都等于相似比
周长之比等于相似比
面积之比等于相似比的平方
(你学到了什么呢?)
谢谢!
同课章节目录
- 第23章 数据分析
- 23.1 平均数与加权平均数
- 23.2 中位数与众数
- 23.3 方差
- 23.4 用样本估计总体
- 第24章 一元二次方程
- 24.1 一元二次方程
- 24.2 解一元二次方程
- 24.3 一元二次方程根与系数的关系
- 24.4 一元二次方程的应用
- 第25章 图形的相似
- 25.1 比例线段
- 25.2 平行线分线段成比例
- 25.3 相似三角形
- 25.4 相似三角形的判定
- 25.5 相似三角形的性质
- 25.6 相似三角形的应用
- 25.7 相似多边形和图形的位似
- 第26章 解直角三角形
- 26.1 锐角三角函数
- 26.2 锐角三角函数的计算
- 26.3 解直角三角形
- 26.4 解直角三角形的应用
- 第27章 反比例函数
- 27.1 反比例函数
- 27.2 反比例函数的图像和性质
- 27.3 反比例函数的应用
- 第28章 圆
- 28.1 圆的概念和性质
- 28.2 过三点的圆
- 28.3 圆心角和圆周角
- 28.4 垂径定理
- 28.5 弧长和扇形面积
