2021-2022学年人教版八年级数学上册11.3.2 多边形的内角和 课后练习(word版、含答案解析)
文档属性
| 名称 | 2021-2022学年人教版八年级数学上册11.3.2 多边形的内角和 课后练习(word版、含答案解析) |

|
|
| 格式 | zip | ||
| 文件大小 | 314.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-21 09:38:53 | ||
图片预览



文档简介
多边形的内角和
一、单选题
1.若正多边形的一个外角是,则该正多边形的边数是(
)
A.3
B.4
C.5
D.6
2.已知一个多边形的内角和等于外角和,则这个多边形是( )
A.三角形
B.四边形
C.五边形
D.六边形
3.如图,在四边形中,,,将沿翻折,得到.若,,则的度数为(
)
A.
B.
C.
D.
4.如图,在四边形中,,与,相邻的外角都是110°,则的外角的度数是(
)
A.90°
B.85°
C.80°
D.70°
5.一个多边形每个外角都等于,则从这个多边形的某个顶点画对角线,最多可以画出几条(
)
A.7条
B.8条
C.9条
D.10条
6.如图,的结果为(
)
A.300°
B.360°
C.400°
D.480°
7.一个正五边形和一个正六边形按如图所示方式摆放,它们都有一边在直线上,且有一个公共顶点,则的度数是(
)
A.75°
B.80°
C.84°
D.90°
8.如果一个四边形四个内角度数之比是1:2:3:4,那么这四个内角中( ).
A.只有一个直角
B.只有一个锐角
C.有两个直角
D.有两个钝角
9.若一个多边形的内角和是它的外角和的3倍,则经过这个多边形的一个顶点最多可以画对角线的条数是(
)
A.8条
B.7条
C.6条
D.5条
10.若一个多边形的内角和是720°,则这个多边形的边数为( )
A.4
B.5
C.6
D.7
11.在现实生活中,铺地最常见的是用正方形地板砖,某小区广场准备用多种地板砖组合铺设,则能够选择的组合是( )
A.正六边形,正八边形
B.正方形,正七边形
C.正五边形,正六边形
D.正三角形,正方形
二、填空题
12.已知正n边形的一个内角为,则n的值是_____________.
13.如果一个多边形的每个内角都相等,且内角的度数是与它相邻的外角度数的2倍,那么这个边形是________边形.
14.如图,五边形ABCDE中x的值为_______.
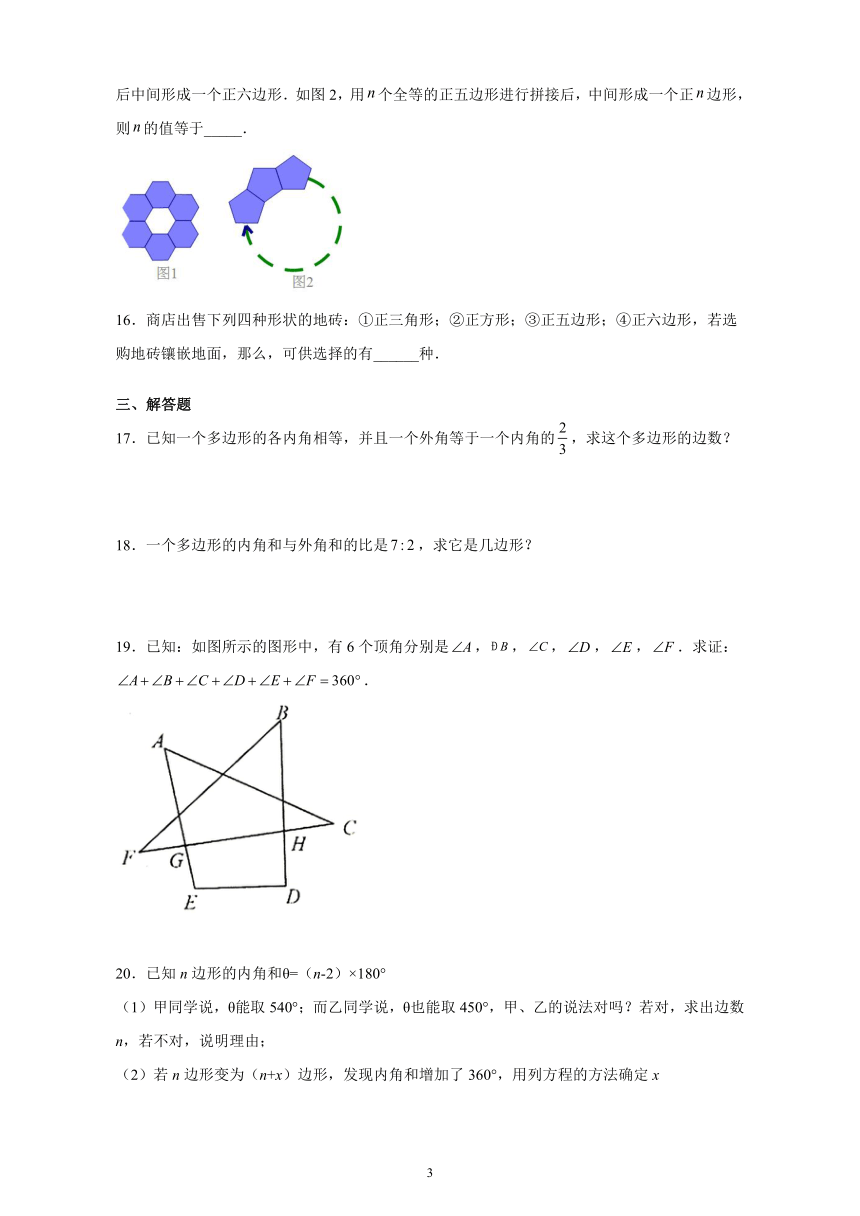
15.如图1,用6个全等的正六边形进行拼接,使相等的两个正六边形有一条公共边,围成一圈后中间形成一个正六边形.如图2,用个全等的正五边形进行拼接后,中间形成一个正边形,则的值等于_____.
16.商店出售下列四种形状的地砖:①正三角形;②正方形;③正五边形;④正六边形,若选购地砖镶嵌地面,那么,可供选择的有______种.
三、解答题
17.已知一个多边形的各内角相等,并且一个外角等于一个内角的,求这个多边形的边数?
18.一个多边形的内角和与外角和的比是,求它是几边形?
19.已知:如图所示的图形中,有6个顶角分别是,,,,,.求证:.
20.已知n边形的内角和θ=(n-2)×180°
(1)甲同学说,θ能取540°;而乙同学说,θ也能取450°,甲、乙的说法对吗?若对,求出边数n,若不对,说明理由;
(2)若n边形变为(n+x)边形,发现内角和增加了360°,用列方程的方法确定x
参考答案
1.D
解:360°÷60°=6.
故该正多边形的边数为6.
故选:D.
2.B
解:设这个多边形边数为,
由题意得,,
解得,
所以,这个多边形是四边形.
故选:B.
3.B
解:∵MF∥AD,FN∥DC,∠A=110°,∠C=80°,
∴∠BMF=110°,∠FNB=80°,
∵将△BMN沿MN翻折得△FMN,
∴∠FMN=∠BMN=55°,∠FNM=∠MNB=40°,
∴∠D=∠B=180°?55°?40°=85°,
故选:B.
4.D
解:在四边形中,,
相邻的外角度数为:,
.
故选:.
5.A
解:根据题意可知多边形为正多边形,设边数为
则由多边形外角和的性质可得,解得
则从一个顶点最多可以画10-3=7条对角线
故选:A
6.B
解:因为,
,
四边形的外角和是,
故选:B.
7.C
解:由题意:∠AOE=108°,∠BOF=120°,∠OEF=72°,∠OFE=60°,
∴∠EOF=180°?72°?60°=48°,
∴∠AOB=360°?108°?48°?120°=84°,
故选C.
8.D
解:一个四边形四个内角的度数之比为,
∴四个内角的度数分别为:;
;
;
.
∴这个四边形的内角中有两个钝角.
故选:D.
9.D
解:设这个多边形有条边,由题意得:
,
解得,
从这个多边形的一个顶点出发的对角线的条数是,
故选:.
10.C
解:(n?2)×180°=720°,
∴n?2=4,
∴n=6.
∴这个多边形的边数为6.
故选:C.
11.D
解:∵正三角形的每个内角60°,
正方形的每个内角是90°,
正五边形的每个内角是108°,
正六边形的每个内角是120°,
正七边形的每个内角是
正八边形每个内角是180°-360°÷8=135°,
∴能够组合是正三角形,正方形,
故选:D.
12.8
解:∵正n边形的一个内角为,
∴,
解得:;
故答案是8.
13.六
解:设多边形的外角的度数是x,则内角是2x,
则x+2x=180°,
解得:x=60°,
则这个多边形的边数是:360°÷60°=6.
故答案为:六
14.
解:
.
故答案为:.
15.10
解:正五边形的每一个内角为
则正五边形围成的多边形的一个内角的度数为:
解得
故答案为:
16.3
解:①正三角形的每个内角是60°,能整除360°,6个能组成镶嵌
②正方形的每个内角是90°,4个能组成镶嵌;
③正五边形每个内角是180°?360°÷5=108°,不能整除360°,不能镶嵌;
④正六边形的每个内角是120°,能整除360°,3个能组成镶嵌;
故若只选购其中某一种地砖镶嵌地面,可供选择的地砖共有3种.
故答案为:3.
17.这个多边形的边数为5
解:设多边形的一个内角为度,则一个外角为度,依题意得:
,
,
解得:,
.
答:这个多边形的边数为5.
18.九边形
解:设这个多边形的边数为,
则有,
解得:.
这个多边形的边数为9,
故它是九边形.
19.见解析
解:证明:∵是的一个外角,
∴(三角形的一个外角等于和它不相邻的两个内角的和).
同理,.
∴(四边形的内角和等于360°).
20.(1)甲对,乙不对,理由见解析;(2)x=2.
解:(1)甲对,乙不对.理由如下:
∵当θ取540°时,540°=(n-2)×180°,
解得n=5;
当θ取450°时,450°=(n-2)×180°,
解得n=;
∵n为整数,
∴θ不能取450°;
(2)依题意得,
(n-2)×180°+360°=(n+x-2)×180°,
解得x=2.
一、单选题
1.若正多边形的一个外角是,则该正多边形的边数是(
)
A.3
B.4
C.5
D.6
2.已知一个多边形的内角和等于外角和,则这个多边形是( )
A.三角形
B.四边形
C.五边形
D.六边形
3.如图,在四边形中,,,将沿翻折,得到.若,,则的度数为(
)
A.
B.
C.
D.
4.如图,在四边形中,,与,相邻的外角都是110°,则的外角的度数是(
)
A.90°
B.85°
C.80°
D.70°
5.一个多边形每个外角都等于,则从这个多边形的某个顶点画对角线,最多可以画出几条(
)
A.7条
B.8条
C.9条
D.10条
6.如图,的结果为(
)
A.300°
B.360°
C.400°
D.480°
7.一个正五边形和一个正六边形按如图所示方式摆放,它们都有一边在直线上,且有一个公共顶点,则的度数是(
)
A.75°
B.80°
C.84°
D.90°
8.如果一个四边形四个内角度数之比是1:2:3:4,那么这四个内角中( ).
A.只有一个直角
B.只有一个锐角
C.有两个直角
D.有两个钝角
9.若一个多边形的内角和是它的外角和的3倍,则经过这个多边形的一个顶点最多可以画对角线的条数是(
)
A.8条
B.7条
C.6条
D.5条
10.若一个多边形的内角和是720°,则这个多边形的边数为( )
A.4
B.5
C.6
D.7
11.在现实生活中,铺地最常见的是用正方形地板砖,某小区广场准备用多种地板砖组合铺设,则能够选择的组合是( )
A.正六边形,正八边形
B.正方形,正七边形
C.正五边形,正六边形
D.正三角形,正方形
二、填空题
12.已知正n边形的一个内角为,则n的值是_____________.
13.如果一个多边形的每个内角都相等,且内角的度数是与它相邻的外角度数的2倍,那么这个边形是________边形.
14.如图,五边形ABCDE中x的值为_______.
15.如图1,用6个全等的正六边形进行拼接,使相等的两个正六边形有一条公共边,围成一圈后中间形成一个正六边形.如图2,用个全等的正五边形进行拼接后,中间形成一个正边形,则的值等于_____.
16.商店出售下列四种形状的地砖:①正三角形;②正方形;③正五边形;④正六边形,若选购地砖镶嵌地面,那么,可供选择的有______种.
三、解答题
17.已知一个多边形的各内角相等,并且一个外角等于一个内角的,求这个多边形的边数?
18.一个多边形的内角和与外角和的比是,求它是几边形?
19.已知:如图所示的图形中,有6个顶角分别是,,,,,.求证:.
20.已知n边形的内角和θ=(n-2)×180°
(1)甲同学说,θ能取540°;而乙同学说,θ也能取450°,甲、乙的说法对吗?若对,求出边数n,若不对,说明理由;
(2)若n边形变为(n+x)边形,发现内角和增加了360°,用列方程的方法确定x
参考答案
1.D
解:360°÷60°=6.
故该正多边形的边数为6.
故选:D.
2.B
解:设这个多边形边数为,
由题意得,,
解得,
所以,这个多边形是四边形.
故选:B.
3.B
解:∵MF∥AD,FN∥DC,∠A=110°,∠C=80°,
∴∠BMF=110°,∠FNB=80°,
∵将△BMN沿MN翻折得△FMN,
∴∠FMN=∠BMN=55°,∠FNM=∠MNB=40°,
∴∠D=∠B=180°?55°?40°=85°,
故选:B.
4.D
解:在四边形中,,
相邻的外角度数为:,
.
故选:.
5.A
解:根据题意可知多边形为正多边形,设边数为
则由多边形外角和的性质可得,解得
则从一个顶点最多可以画10-3=7条对角线
故选:A
6.B
解:因为,
,
四边形的外角和是,
故选:B.
7.C
解:由题意:∠AOE=108°,∠BOF=120°,∠OEF=72°,∠OFE=60°,
∴∠EOF=180°?72°?60°=48°,
∴∠AOB=360°?108°?48°?120°=84°,
故选C.
8.D
解:一个四边形四个内角的度数之比为,
∴四个内角的度数分别为:;
;
;
.
∴这个四边形的内角中有两个钝角.
故选:D.
9.D
解:设这个多边形有条边,由题意得:
,
解得,
从这个多边形的一个顶点出发的对角线的条数是,
故选:.
10.C
解:(n?2)×180°=720°,
∴n?2=4,
∴n=6.
∴这个多边形的边数为6.
故选:C.
11.D
解:∵正三角形的每个内角60°,
正方形的每个内角是90°,
正五边形的每个内角是108°,
正六边形的每个内角是120°,
正七边形的每个内角是
正八边形每个内角是180°-360°÷8=135°,
∴能够组合是正三角形,正方形,
故选:D.
12.8
解:∵正n边形的一个内角为,
∴,
解得:;
故答案是8.
13.六
解:设多边形的外角的度数是x,则内角是2x,
则x+2x=180°,
解得:x=60°,
则这个多边形的边数是:360°÷60°=6.
故答案为:六
14.
解:
.
故答案为:.
15.10
解:正五边形的每一个内角为
则正五边形围成的多边形的一个内角的度数为:
解得
故答案为:
16.3
解:①正三角形的每个内角是60°,能整除360°,6个能组成镶嵌
②正方形的每个内角是90°,4个能组成镶嵌;
③正五边形每个内角是180°?360°÷5=108°,不能整除360°,不能镶嵌;
④正六边形的每个内角是120°,能整除360°,3个能组成镶嵌;
故若只选购其中某一种地砖镶嵌地面,可供选择的地砖共有3种.
故答案为:3.
17.这个多边形的边数为5
解:设多边形的一个内角为度,则一个外角为度,依题意得:
,
,
解得:,
.
答:这个多边形的边数为5.
18.九边形
解:设这个多边形的边数为,
则有,
解得:.
这个多边形的边数为9,
故它是九边形.
19.见解析
解:证明:∵是的一个外角,
∴(三角形的一个外角等于和它不相邻的两个内角的和).
同理,.
∴(四边形的内角和等于360°).
20.(1)甲对,乙不对,理由见解析;(2)x=2.
解:(1)甲对,乙不对.理由如下:
∵当θ取540°时,540°=(n-2)×180°,
解得n=5;
当θ取450°时,450°=(n-2)×180°,
解得n=;
∵n为整数,
∴θ不能取450°;
(2)依题意得,
(n-2)×180°+360°=(n+x-2)×180°,
解得x=2.
