2021-2022学年人教版数学八年级上册12.2三角形全等的判定课后练习 (word版、含解析)
文档属性
| 名称 | 2021-2022学年人教版数学八年级上册12.2三角形全等的判定课后练习 (word版、含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 585.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-21 09:40:57 | ||
图片预览


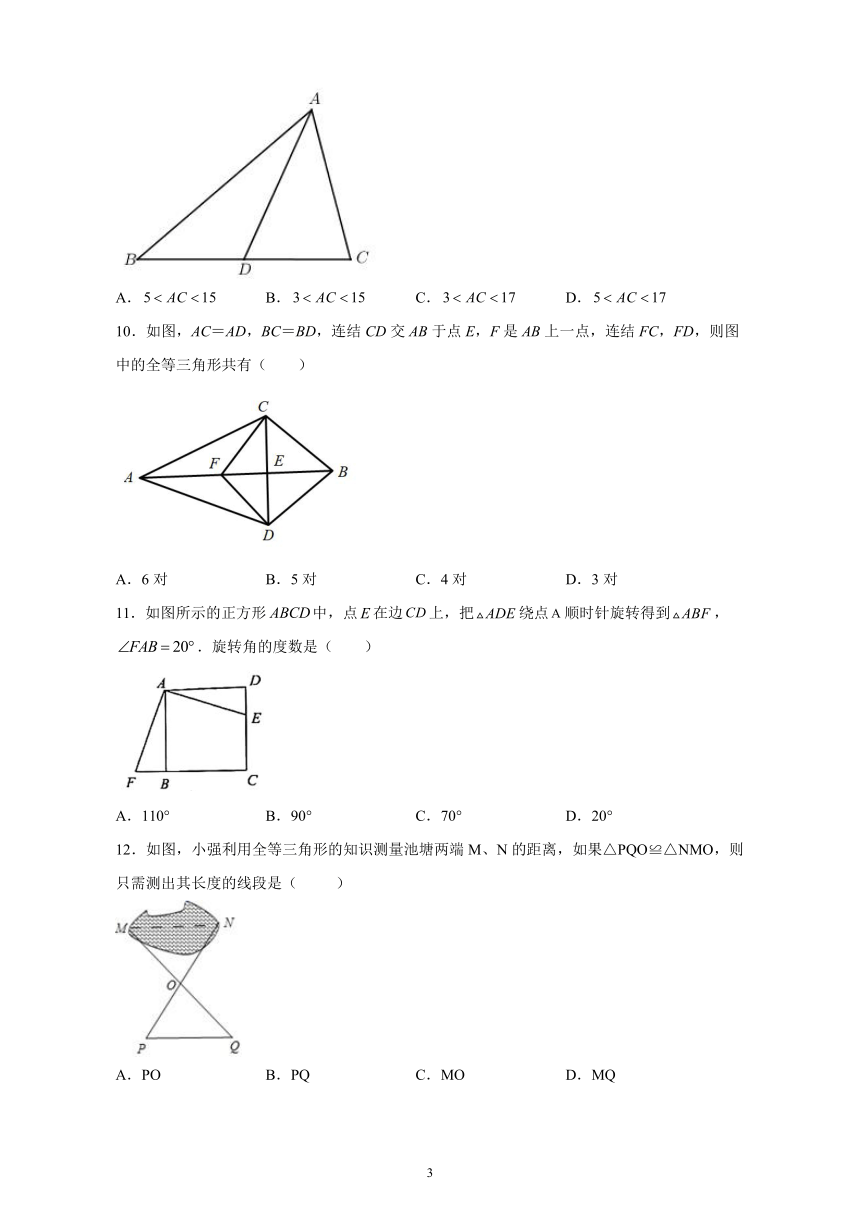
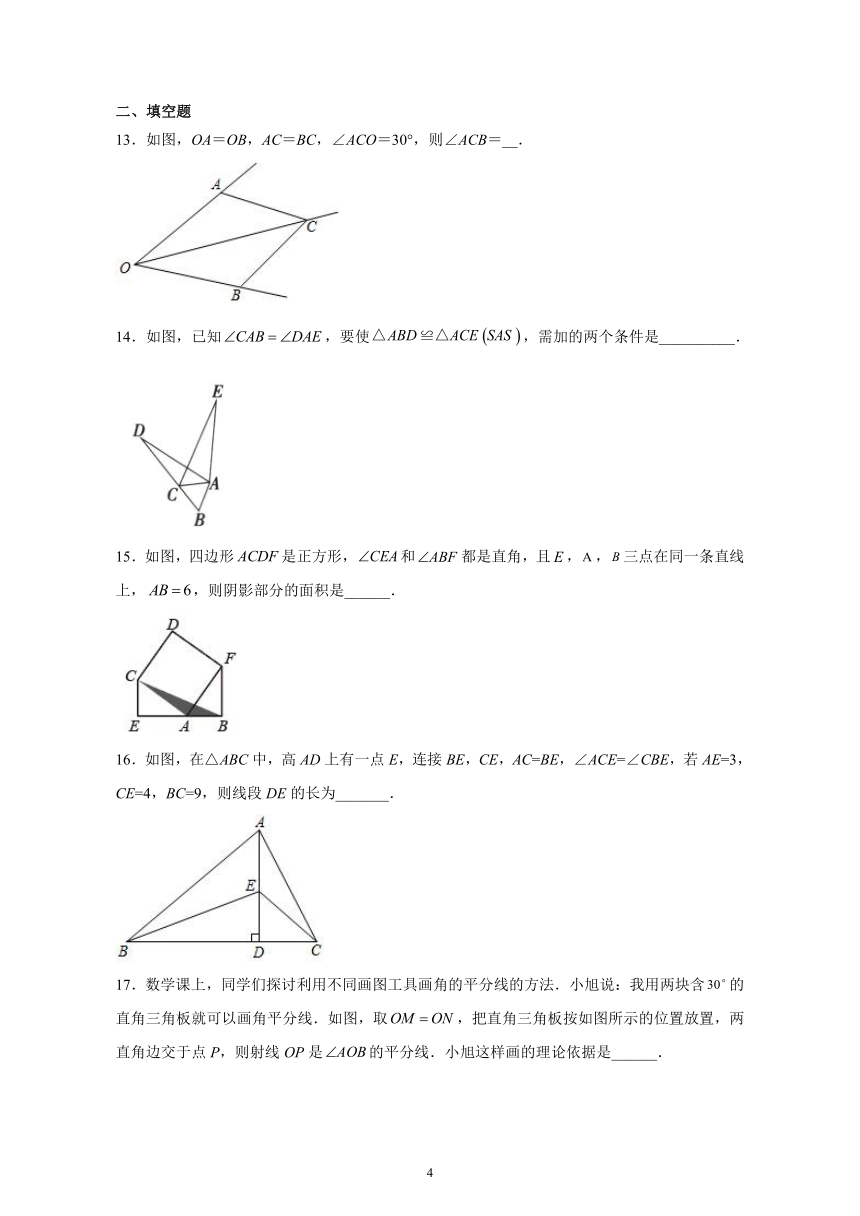
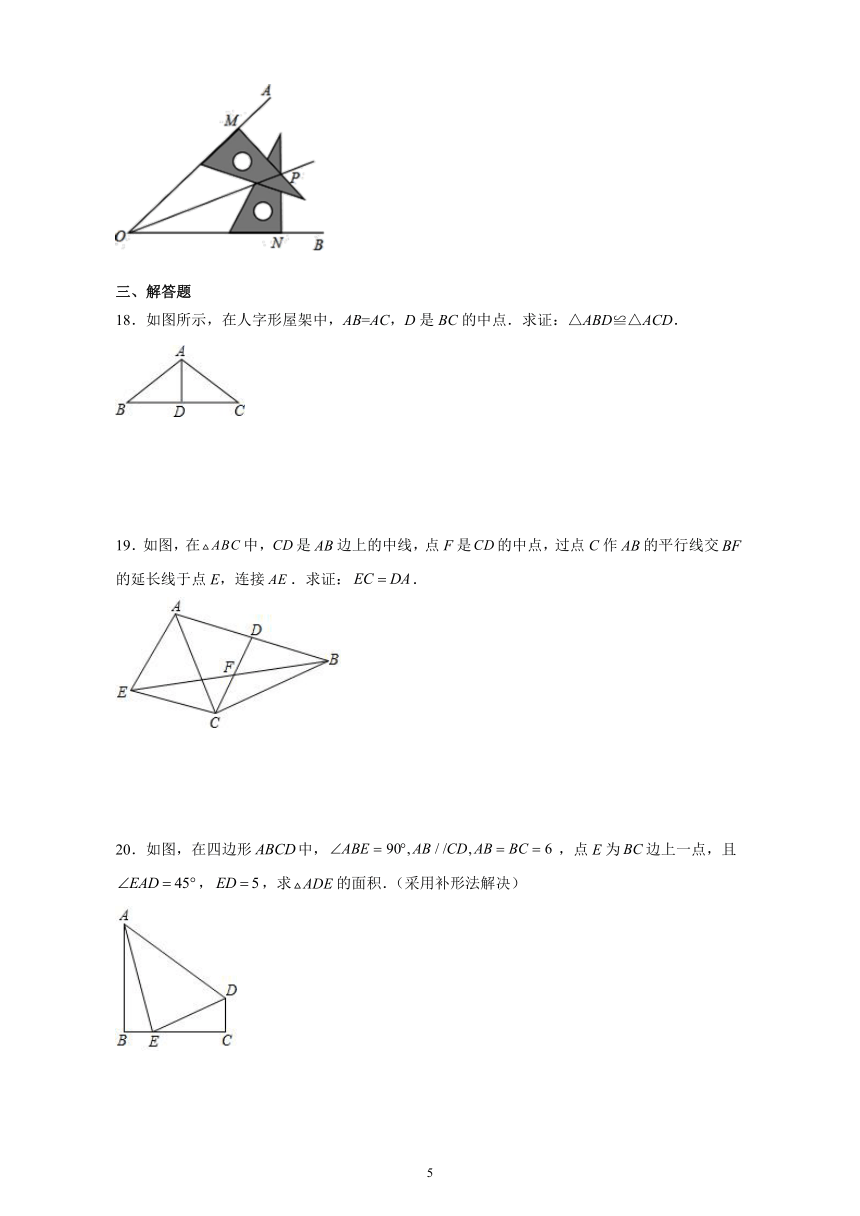
文档简介
三角形全等的判定
一、单选题
1.如图,在中,,中线和相交于点F,,则图中可用证出的全等三角形共有(
)
A.1对
B.2对
C.3对
D.4对
2.如图,在△ABC中,AB=AC,D为BC的中点,则下列结论中:①△ABD≌△ACD;②∠B=∠C;③AD平分∠BAC;④AD⊥BC,其中正确的个数为(
)
A.1个
B.2个
C.3个
D.4个
3.如图,已知平分,那么就可以证明,理由是(
)
A.
B.
C.
D.
4.如图,在△ABC与△EMN中,,,∠C=∠M=54°,若∠A=66°,则下列结论正确的是(
)
A.
B.EN=a
C.∠E=60°
D.∠N=66°
5.如图,,判定的理由是(
)
A.
B.
C.
D.无法确定
6.如图,在中,于点D,于点E,与相交于点F,若,则与相等的线段是(
)
A.
B.
C.
D.
7.如图,是等腰直角三角形,,若,垂足分别是点D、E则图中全等的三角形共有(
)
A.2对
B.3对
C.4对
D.5对
8.如图,,,,则能证明的判定法是
A.
B.
C.
D.
9.如图,是的边上的中线,,则的取值范围为(
)
A.
B.
C.
D.
10.如图,AC=AD,BC=BD,连结CD交AB于点E,F是AB上一点,连结FC,FD,则图中的全等三角形共有( )
A.6对
B.5对
C.4对
D.3对
11.如图所示的正方形中,点在边上,把绕点顺时针旋转得到,.旋转角的度数是(
)
A.110°
B.90°
C.70°
D.20°
12.如图,小强利用全等三角形的知识测量池塘两端M、N的距离,如果△PQO≌△NMO,则只需测出其长度的线段是(
)
A.PO
B.PQ
C.MO
D.MQ
二、填空题
13.如图,OA=OB,AC=BC,∠ACO=30°,则∠ACB=__.
14.如图,已知,要使,需加的两个条件是__________.
15.如图,四边形是正方形,和都是直角,且,,三点在同一条直线上,,则阴影部分的面积是______.
16.如图,在△ABC中,高AD上有一点E,连接BE,CE,AC=BE,∠ACE=∠CBE,若AE=3,CE=4,BC=9,则线段DE的长为_______.
17.数学课上,同学们探讨利用不同画图工具画角的平分线的方法.小旭说:我用两块含的直角三角板就可以画角平分线.如图,取,把直角三角板按如图所示的位置放置,两直角边交于点P,则射线OP是的平分线.小旭这样画的理论依据是______.
三、解答题
18.如图所示,在人字形屋架中,AB=AC,D是BC的中点.求证:△ABD≌△ACD.
19.如图,在中,是边上的中线,点F是的中点,过点C作的平行线交的延长线于点E,连接.求证:.
20.如图,在四边形中,,点E为边上一点,且,,求的面积.(采用补形法解决)
21.如图,已知.求证:.
22.如图,在五边形中,.
(1)求证:;(时,)
(2)当时,求的度数.(五边形的内角和是)
参考答案
1.C
解:∵分别是中线,
∴,
∵,
∴.
在和中,
∵
∴;
在和中,
∵
∴
∴∠DBC=∠ECB,
∴FB=FC,
∴EF=EC-FC=BD-FB=FD,
在和中,
∵
∴≌(SSS)
故可由证出3对全等三角形.
故选择C.
2.D
解:∵D为BC的中点,
∴BD=CD,
又∵AB=AC,AD为公共边
∴△ABD≌△ACD(SSS),故①正确,
∴∠B=∠C,∠BAD=∠CAD,∠ADB=∠ADC,
∵∠ADB+∠ADC=180°,
∴∠ADB=∠ADC=90°,即AD⊥BC,故②③④正确.
综上所述:正确的结论有①②③④共4个,
故选D.
3.C
解:∵平分,
∴,
在和中,
∴
故选C
4.A
解:在与中,
所以:
所以B,C,D,都错误,A正确.
故选A.
5.A
解:∵,
∴,
∵和为对顶角,
∴,
又∵,
∴.
故选:A.
6.B
解:∵于点D,于点E,,
∴,
∵,∴,
在和中,
,
∴,
∴.
7.A
解:∵,,,,
∴,
同理可证明.
故选A.
8.D
解:∵,,
∴与均为直角三角形,
又,,
∴,
故选:D.
9.C
解:如图,延长至点E,使,连接.
∵为的边上的中线,
∴,
在和中,
∴,
∴.
在中,,
即,
∴,
故选:C.
10.A
解:在△ACB和ADB中,
,
∴△ACB≌ADB,
∴∠CAB=∠DAB,∠CBA=∠DBA,
∵AC=AD,∠CAB=∠DAB,AF=AF
∴△CAF≌△DAF,CF=DF,
∵AC=AD,∠CAB=∠DAB,AE=AE
∴△ACE≌△ADE,CE=DE,
∵BC=BD,∠CBA=∠DBA,BE=BE
∴△CBE≌△DBE,
∵BC=BD,∠CBA=∠DBA,BF=BF
∴△FCB≌△FDB,
∵CF=DF,CE=DE,EF=EF,
∴△CEF≌△DEF,
∴图中全等的三角形有6对,
故选:A.
11.B
解:∵四边形ABCD是正方形,
∴AB=AD,∠BAD=,
由旋转得≌,
∴∠FAB=∠EAD,
∴∠FAB+∠∠BAE=∠EAD+∠BAE,
∴∠FAE=∠BAD=,
∴旋转角的度数是,
故选:B.
12.B
解:要想利用△PQO≌△NMO求得MN的长,只需求得线段PQ的长,故选B.
13.60°
解:在△ACO和△BCO中,
,
∴△AOC≌△BOC(SSS),
∴∠BCO=∠ACO=30°,
∴∠ACB=∠BCO+∠ACO=60°,
故答案为:60°.
14.
解:∵,
∴,
当时,得到;
故答案是:.
15.18
解:∵四边形ACDF是正方形,
∴AC=AF,∠CAF=90°,
∴∠CAE+∠FAB=90°,∠ACE+∠CAE=90°,
∴∠ACE=∠FAB,且∠E=∠ABF,AC=AF,
∴△ACE≌△FAB(AAS),
∴CE=AB=6,
∴S阴影=×AB×CE=18,
故答案为:18.
16.
解:过点作交于点,如图,
,
,
,
,
,
,
,
,
,
(ASA),
,,
,
,
,
,
故答案为:.
17.HL
解:∵∠OMP=∠ONP=90°,且OM=ON,OP=OP,
∴Rt△OMP≌Rt△ONP(HL),
∴∠MOP=∠NOP,
∴OP是∠AOB的平分线.
故答案为:HL.
18.见解析
解:证明:∵D是的中点,
∴,
在和中,
∵,
∴.
19.见解析
解:证明:∵,
∴,
∵点F是的中点,
∴,
在和中,
∴,
∴,
∵是边上的中线,
∴,
∴.
20.15
解:如图,过点A作交的延长线于点F,
∴∠AFC=90°,
∵∠ABE=90°,AB∥CD,
∴∠ABE=∠BCD=90°,即∠AFC=∠ABE=∠BCD=90°,
∴四边形ABCF是矩形,
∵AB=BC=6,
∴四边形ABCF是正方形,
延长到点G,使,连接.
在△AGB和△ADF中,
∴△AGB≌△ADF(SAS),
∴,
,
∵,
∴,
∵,
∴,
在△ADE和△AGE中,
∴△ADE≌△AGE(SAS),
∴,
∴.
21.见解析
解:证明:∵,
∴,
又∵,
∴,
∴,
∴.
22.(1)见解析;(2)80°
解:(1)证明:∵,
∴,
又∵,
∴,
在和中,
,
∴;
(2)解:∵,,
∴,
又∵,
∴在五边形中,.
一、单选题
1.如图,在中,,中线和相交于点F,,则图中可用证出的全等三角形共有(
)
A.1对
B.2对
C.3对
D.4对
2.如图,在△ABC中,AB=AC,D为BC的中点,则下列结论中:①△ABD≌△ACD;②∠B=∠C;③AD平分∠BAC;④AD⊥BC,其中正确的个数为(
)
A.1个
B.2个
C.3个
D.4个
3.如图,已知平分,那么就可以证明,理由是(
)
A.
B.
C.
D.
4.如图,在△ABC与△EMN中,,,∠C=∠M=54°,若∠A=66°,则下列结论正确的是(
)
A.
B.EN=a
C.∠E=60°
D.∠N=66°
5.如图,,判定的理由是(
)
A.
B.
C.
D.无法确定
6.如图,在中,于点D,于点E,与相交于点F,若,则与相等的线段是(
)
A.
B.
C.
D.
7.如图,是等腰直角三角形,,若,垂足分别是点D、E则图中全等的三角形共有(
)
A.2对
B.3对
C.4对
D.5对
8.如图,,,,则能证明的判定法是
A.
B.
C.
D.
9.如图,是的边上的中线,,则的取值范围为(
)
A.
B.
C.
D.
10.如图,AC=AD,BC=BD,连结CD交AB于点E,F是AB上一点,连结FC,FD,则图中的全等三角形共有( )
A.6对
B.5对
C.4对
D.3对
11.如图所示的正方形中,点在边上,把绕点顺时针旋转得到,.旋转角的度数是(
)
A.110°
B.90°
C.70°
D.20°
12.如图,小强利用全等三角形的知识测量池塘两端M、N的距离,如果△PQO≌△NMO,则只需测出其长度的线段是(
)
A.PO
B.PQ
C.MO
D.MQ
二、填空题
13.如图,OA=OB,AC=BC,∠ACO=30°,则∠ACB=__.
14.如图,已知,要使,需加的两个条件是__________.
15.如图,四边形是正方形,和都是直角,且,,三点在同一条直线上,,则阴影部分的面积是______.
16.如图,在△ABC中,高AD上有一点E,连接BE,CE,AC=BE,∠ACE=∠CBE,若AE=3,CE=4,BC=9,则线段DE的长为_______.
17.数学课上,同学们探讨利用不同画图工具画角的平分线的方法.小旭说:我用两块含的直角三角板就可以画角平分线.如图,取,把直角三角板按如图所示的位置放置,两直角边交于点P,则射线OP是的平分线.小旭这样画的理论依据是______.
三、解答题
18.如图所示,在人字形屋架中,AB=AC,D是BC的中点.求证:△ABD≌△ACD.
19.如图,在中,是边上的中线,点F是的中点,过点C作的平行线交的延长线于点E,连接.求证:.
20.如图,在四边形中,,点E为边上一点,且,,求的面积.(采用补形法解决)
21.如图,已知.求证:.
22.如图,在五边形中,.
(1)求证:;(时,)
(2)当时,求的度数.(五边形的内角和是)
参考答案
1.C
解:∵分别是中线,
∴,
∵,
∴.
在和中,
∵
∴;
在和中,
∵
∴
∴∠DBC=∠ECB,
∴FB=FC,
∴EF=EC-FC=BD-FB=FD,
在和中,
∵
∴≌(SSS)
故可由证出3对全等三角形.
故选择C.
2.D
解:∵D为BC的中点,
∴BD=CD,
又∵AB=AC,AD为公共边
∴△ABD≌△ACD(SSS),故①正确,
∴∠B=∠C,∠BAD=∠CAD,∠ADB=∠ADC,
∵∠ADB+∠ADC=180°,
∴∠ADB=∠ADC=90°,即AD⊥BC,故②③④正确.
综上所述:正确的结论有①②③④共4个,
故选D.
3.C
解:∵平分,
∴,
在和中,
∴
故选C
4.A
解:在与中,
所以:
所以B,C,D,都错误,A正确.
故选A.
5.A
解:∵,
∴,
∵和为对顶角,
∴,
又∵,
∴.
故选:A.
6.B
解:∵于点D,于点E,,
∴,
∵,∴,
在和中,
,
∴,
∴.
7.A
解:∵,,,,
∴,
同理可证明.
故选A.
8.D
解:∵,,
∴与均为直角三角形,
又,,
∴,
故选:D.
9.C
解:如图,延长至点E,使,连接.
∵为的边上的中线,
∴,
在和中,
∴,
∴.
在中,,
即,
∴,
故选:C.
10.A
解:在△ACB和ADB中,
,
∴△ACB≌ADB,
∴∠CAB=∠DAB,∠CBA=∠DBA,
∵AC=AD,∠CAB=∠DAB,AF=AF
∴△CAF≌△DAF,CF=DF,
∵AC=AD,∠CAB=∠DAB,AE=AE
∴△ACE≌△ADE,CE=DE,
∵BC=BD,∠CBA=∠DBA,BE=BE
∴△CBE≌△DBE,
∵BC=BD,∠CBA=∠DBA,BF=BF
∴△FCB≌△FDB,
∵CF=DF,CE=DE,EF=EF,
∴△CEF≌△DEF,
∴图中全等的三角形有6对,
故选:A.
11.B
解:∵四边形ABCD是正方形,
∴AB=AD,∠BAD=,
由旋转得≌,
∴∠FAB=∠EAD,
∴∠FAB+∠∠BAE=∠EAD+∠BAE,
∴∠FAE=∠BAD=,
∴旋转角的度数是,
故选:B.
12.B
解:要想利用△PQO≌△NMO求得MN的长,只需求得线段PQ的长,故选B.
13.60°
解:在△ACO和△BCO中,
,
∴△AOC≌△BOC(SSS),
∴∠BCO=∠ACO=30°,
∴∠ACB=∠BCO+∠ACO=60°,
故答案为:60°.
14.
解:∵,
∴,
当时,得到;
故答案是:.
15.18
解:∵四边形ACDF是正方形,
∴AC=AF,∠CAF=90°,
∴∠CAE+∠FAB=90°,∠ACE+∠CAE=90°,
∴∠ACE=∠FAB,且∠E=∠ABF,AC=AF,
∴△ACE≌△FAB(AAS),
∴CE=AB=6,
∴S阴影=×AB×CE=18,
故答案为:18.
16.
解:过点作交于点,如图,
,
,
,
,
,
,
,
,
,
(ASA),
,,
,
,
,
,
故答案为:.
17.HL
解:∵∠OMP=∠ONP=90°,且OM=ON,OP=OP,
∴Rt△OMP≌Rt△ONP(HL),
∴∠MOP=∠NOP,
∴OP是∠AOB的平分线.
故答案为:HL.
18.见解析
解:证明:∵D是的中点,
∴,
在和中,
∵,
∴.
19.见解析
解:证明:∵,
∴,
∵点F是的中点,
∴,
在和中,
∴,
∴,
∵是边上的中线,
∴,
∴.
20.15
解:如图,过点A作交的延长线于点F,
∴∠AFC=90°,
∵∠ABE=90°,AB∥CD,
∴∠ABE=∠BCD=90°,即∠AFC=∠ABE=∠BCD=90°,
∴四边形ABCF是矩形,
∵AB=BC=6,
∴四边形ABCF是正方形,
延长到点G,使,连接.
在△AGB和△ADF中,
∴△AGB≌△ADF(SAS),
∴,
,
∵,
∴,
∵,
∴,
在△ADE和△AGE中,
∴△ADE≌△AGE(SAS),
∴,
∴.
21.见解析
解:证明:∵,
∴,
又∵,
∴,
∴,
∴.
22.(1)见解析;(2)80°
解:(1)证明:∵,
∴,
又∵,
∴,
在和中,
,
∴;
(2)解:∵,,
∴,
又∵,
∴在五边形中,.
