2021-2022学年八年级数学人教版上册12.2三角形全等的判定 优生辅导训练(word版、含解析)
文档属性
| 名称 | 2021-2022学年八年级数学人教版上册12.2三角形全等的判定 优生辅导训练(word版、含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 338.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-21 09:54:32 | ||
图片预览

文档简介
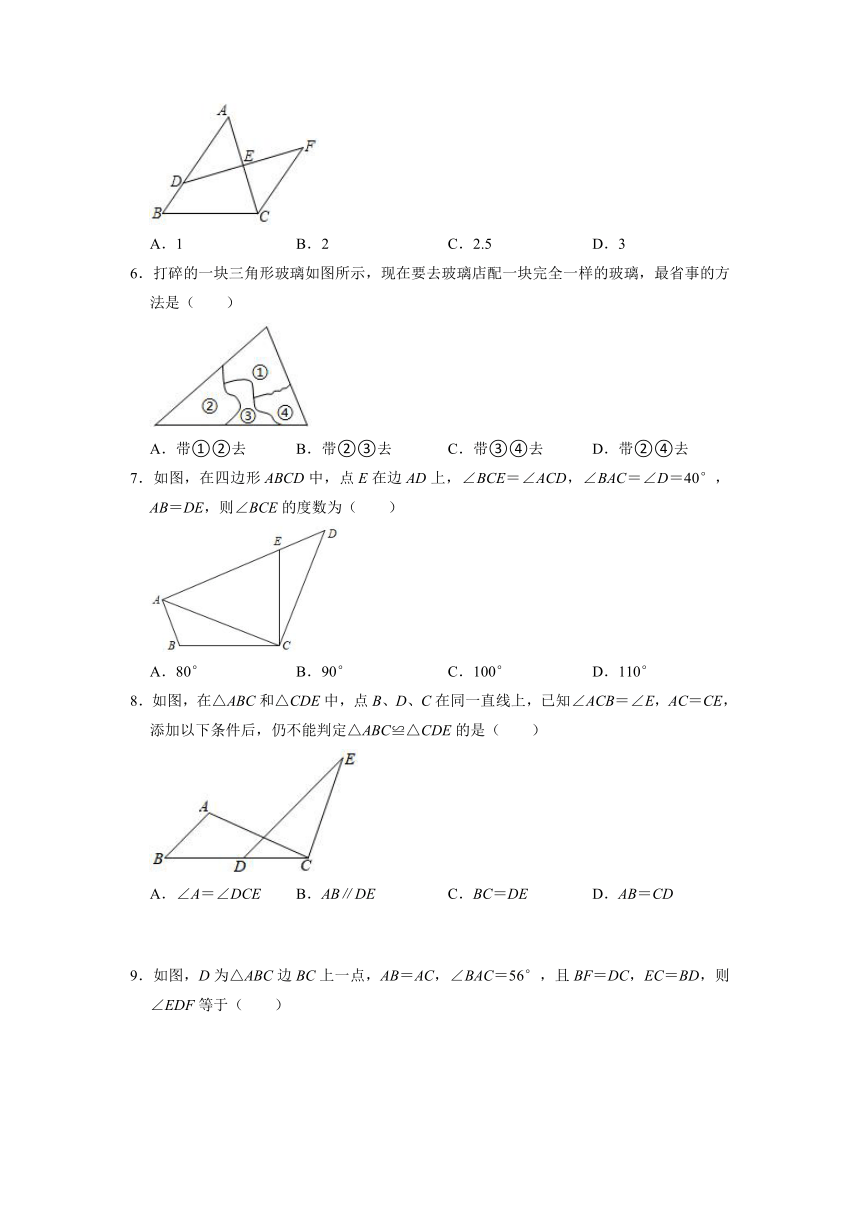
2021-2022学年人教版八年级数学上册《12.2三角形全等的判定》优生辅导训练(附答案)
1.如图,方格中△ABC的三个顶点分别在正方形的顶点(格点上),这样的三角形叫格点三角形,图中可以画出与△ABC全等的格点三角形共有( )个.(不含△ABC)
A.28
B.29
C.30
D.31
2.如图,AD是△ABC的角平分线,∠C=2∠B,F是BC的中点,EF∥AD交AB于点E,且BE=4AE,若CD=4,则AB的长为( )
A.10
B.9
C.8
D.6
3.如图,∠ACB=90°,AC=CD,过点D作AB的垂线交AB的延长线于点E.若AB=2DE,则∠BAC的度数为( )
A.45°
B.30°
C.22.5°
D.15°
4.如图,在△ABC和△DEF中,点B、F、C、D在同一条直线上,已知∠A=∠D,AB=DE,添加以下条件,不能判定△ABC≌△DEF的是( )
A.∠B=∠E
B.AC=DF
C.∠ACD=∠BFE
D.BF=CD
5.如图,E是△ABC的边AC的中点,过点C作CF∥AB,过点E作直线DF交AB于D,交CF于F,若AB=9,CF=6.5,则BD的长为( )
A.1
B.2
C.2.5
D.3
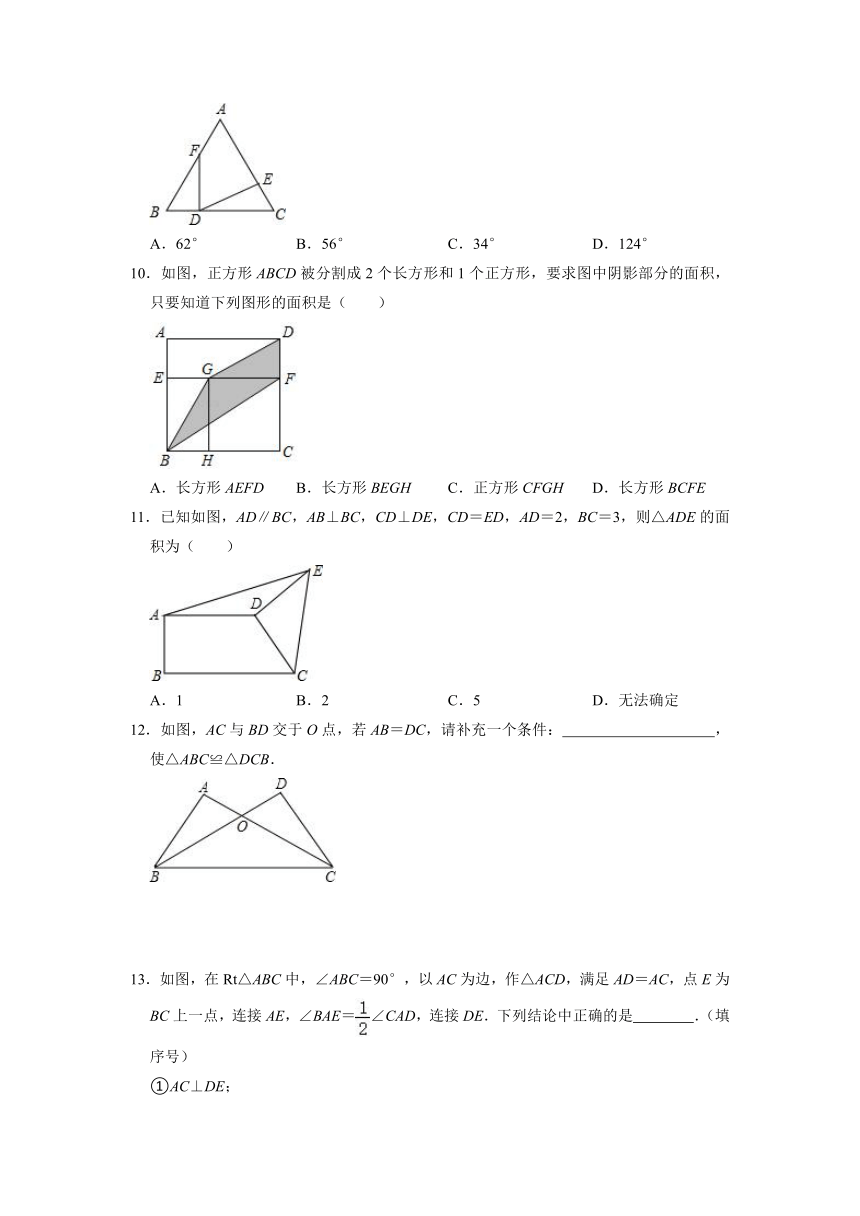
6.打碎的一块三角形玻璃如图所示,现在要去玻璃店配一块完全一样的玻璃,最省事的方法是( )
A.带①②去
B.带②③去
C.带③④去
D.带②④去
7.如图,在四边形ABCD中,点E在边AD上,∠BCE=∠ACD,∠BAC=∠D=40°,AB=DE,则∠BCE的度数为( )
A.80°
B.90°
C.100°
D.110°
8.如图,在△ABC和△CDE中,点B、D、C在同一直线上,已知∠ACB=∠E,AC=CE,添加以下条件后,仍不能判定△ABC≌△CDE的是( )
A.∠A=∠DCE
B.AB∥DE
C.BC=DE
D.AB=CD
9.如图,D为△ABC边BC上一点,AB=AC,∠BAC=56°,且BF=DC,EC=BD,则∠EDF等于( )
A.62°
B.56°
C.34°
D.124°
10.如图,正方形ABCD被分割成2个长方形和1个正方形,要求图中阴影部分的面积,只要知道下列图形的面积是( )
A.长方形AEFD
B.长方形BEGH
C.正方形CFGH
D.长方形BCFE
11.已知如图,AD∥BC,AB⊥BC,CD⊥DE,CD=ED,AD=2,BC=3,则△ADE的面积为( )
A.1
B.2
C.5
D.无法确定
12.如图,AC与BD交于O点,若AB=DC,请补充一个条件:
,使△ABC≌△DCB.
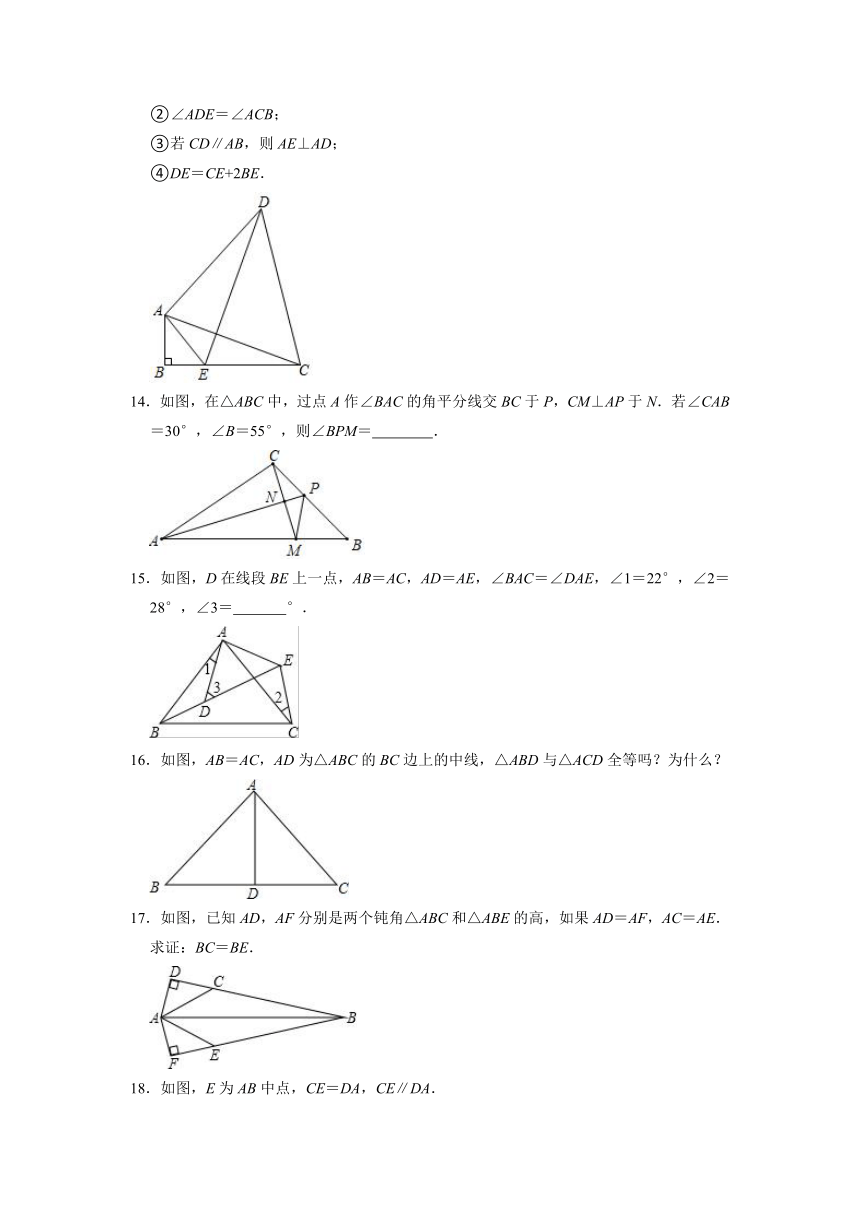
13.如图,在Rt△ABC中,∠ABC=90°,以AC为边,作△ACD,满足AD=AC,点E为BC上一点,连接AE,∠BAE=∠CAD,连接DE.下列结论中正确的是
.(填序号)
①AC⊥DE;
②∠ADE=∠ACB;
③若CD∥AB,则AE⊥AD;
④DE=CE+2BE.
14.如图,在△ABC中,过点A作∠BAC的角平分线交BC于P,CM⊥AP于N.若∠CAB=30°,∠B=55°,则∠BPM=
.
15.如图,D在线段BE上一点,AB=AC,AD=AE,∠BAC=∠DAE,∠1=22°,∠2=28°,∠3=
°.
16.如图,AB=AC,AD为△ABC的BC边上的中线,△ABD与△ACD全等吗?为什么?
17.如图,已知AD,AF分别是两个钝角△ABC和△ABE的高,如果AD=AF,AC=AE.
求证:BC=BE.
18.如图,E为AB中点,CE=DA,CE∥DA.
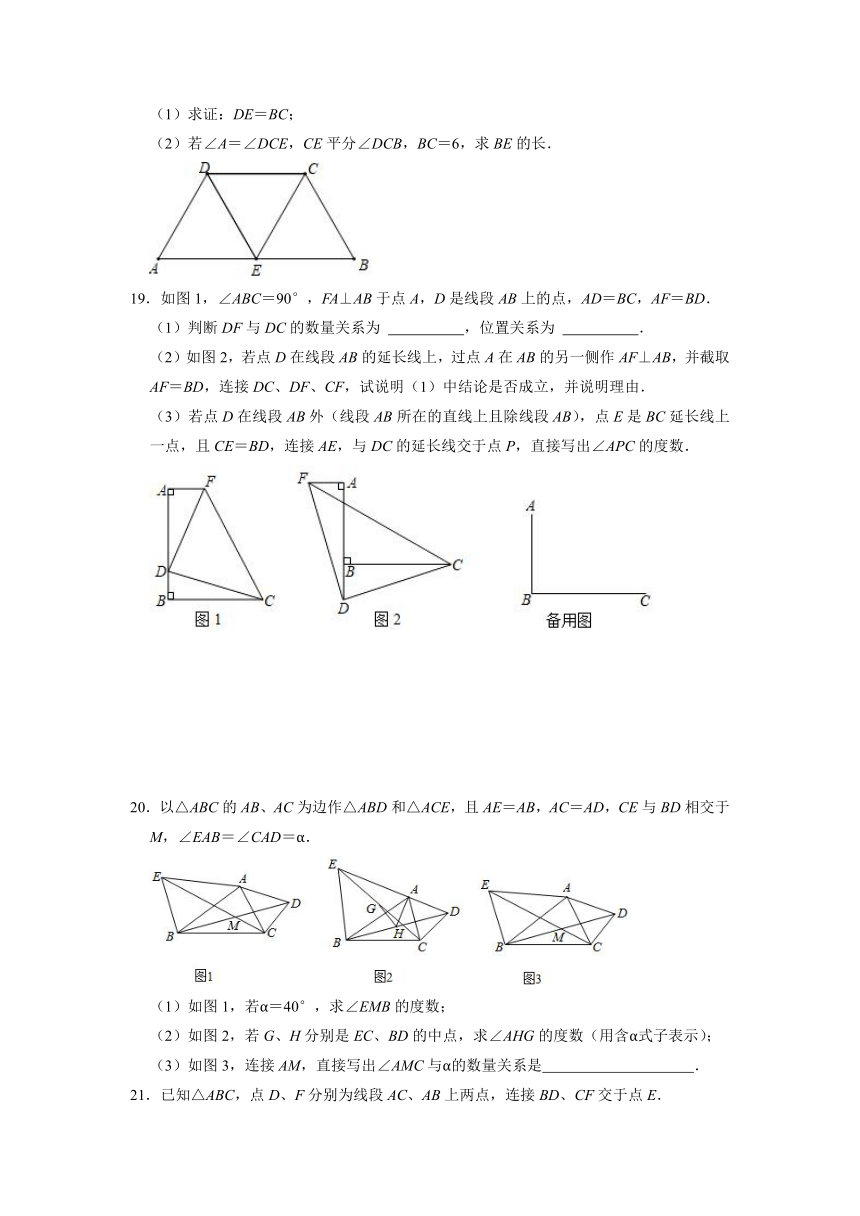
(1)求证:DE=BC;
(2)若∠A=∠DCE,CE平分∠DCB,BC=6,求BE的长.
19.如图1,∠ABC=90°,FA⊥AB于点A,D是线段AB上的点,AD=BC,AF=BD.
(1)判断DF与DC的数量关系为
,位置关系为
.
(2)如图2,若点D在线段AB的延长线上,过点A在AB的另一侧作AF⊥AB,并截取AF=BD,连接DC、DF、CF,试说明(1)中结论是否成立,并说明理由.
(3)若点D在线段AB外(线段AB所在的直线上且除线段AB),点E是BC延长线上一点,且CE=BD,连接AE,与DC的延长线交于点P,直接写出∠APC的度数.
20.以△ABC的AB、AC为边作△ABD和△ACE,且AE=AB,AC=AD,CE与BD相交于M,∠EAB=∠CAD=α.
(1)如图1,若α=40°,求∠EMB的度数;
(2)如图2,若G、H分别是EC、BD的中点,求∠AHG的度数(用含α式子表示);
(3)如图3,连接AM,直接写出∠AMC与α的数量关系是
.
21.已知△ABC,点D、F分别为线段AC、AB上两点,连接BD、CF交于点E.
(1)若BD⊥AC,CF⊥AB,如图1所示,试说明∠BAC+∠BEC=180°;
(2)若BD平分∠ABC,CF平分∠ACB,如图2所示,试说明此时∠BAC与∠BEC的数量关系;
(3)在(2)的条件下,若∠BAC=60°,试说明:EF=ED.
22.如图,AE与BD相交于点C,AC=EC,BC=DC,AB=6cm,点P从点A出发,沿A→B→A方向以3cm/s的速度运动,点Q从点D出发,沿D→E方向以1cm/s的速度运动,P、Q两点同时出发.当点P到达点A时,P、Q两点同时停止运动.设点P的运动时间为t(s).
(1)求证:AB∥DE.
(2)写出线段BP的长(用含t的式子表示).
(3)连接PQ,当线段PQ经过点C时,求t的值.
参考答案
1.解:当点B在下面时,根据平移,对称,可得与△ABC全等的三角形有8个,包括△ABC,
当点B在其它3条边上时,有3×8=24(个)三角形与△ABC全等,
∴一共有:8+24﹣1=31(个)三角形与△ABC全等,
故选:D.
2.解:如图作DG⊥AC于G,DH⊥AB于H,在AB上截取AM=AC,
∵DA平分∠BAC,
∴DG=DH,
∴===,
设BF=FC=4a,
∵EF∥AD,
∴FD=a,CD=3a=4,
∴a=,BD=5a=,
在△ADM和△ADC中,
,
∴△DAM≌△DAC(SAS),
∴DM=DC,∠AMD=∠C,
∵∠C=2∠B,
∴∠AMD=∠B+∠MDB=2∠B,
∴∠B=∠MDB,
∴BM=MD=CD=4,设AC=AM=x,
∴x=6,
∴AB=BM+AC=4+6=10,
故选:A.
3.解:连接AD,延长AC、DE交于M,
∵∠ACB=90°,AC=CD,
∴∠DAC=∠ADC=45°,
∵∠ACB=90°,DE⊥AB,
∴∠DEB=90°=∠ACB=∠DCM,
∵∠ABC=∠DBE,
∴由三角形内角和定理得:∠CAB=∠CDM,
在△ACB和△DCM中
∴△ACB≌△DCM(ASA),
∴AB=DM,
∵AB=2DE,
∴DM=2DE,
∴DE=EM,
∵DE⊥AB,
∴AD=AM,
∴∠BAC=∠DAE=∠DAC==22.5°,
故选:C.
4.解:A.符合全等三角形的判定定理ASA,能推出△ABC≌△DEF,故本选项不符合题意;
B.符合全等三角形的判定定理SAS,能推出△ABC≌△DEF,故本选项不符合题意;
C.∵∠ACD=∠BFE,∠ACD=∠A+∠ABC,∠BFE=∠E+∠D,∠A=∠D,
∴∠B=∠E,
即符合全等三角形的判定定理ASA,能推出△ABC≌△DEF,故本选项不符合题意;
D.∵BF=CD,
∴BF+CF=CD+CF,
即BC=DF,
∵∠A=∠D,AB=DE,
∴不符合全等三角形的判定定理,不能推出△ABC≌△DEF,故本选项符合题意;
故选:D.
5.证明:∵CF∥AB,
∴∠1=∠F,∠2=∠A,
∵点E为AC的中点,
∴AE=EC,
在△ADE和△CFE中
,
∴△ADE≌△CFE(AAS),
∴AD=CF=6.5,
∵AB=9,
∴BD=AB﹣AD=9﹣6.5=2.5,
故选:C.
6.解:A、带①②去,符合ASA判定,选项符合题意;
B、带②③去,仅保留了原三角形的一个角和部分边,不符合任何判定方法,选项不符合题意;
C、带③④去,仅保留了原三角形的一个角和部分边,不符合任何判定方法,选项不符合题意;
D、带②④去,仅保留了原三角形的两个角和部分边,不符合任何判定方法,选项不符合题意;
故选:A.
7.解:∵∠BCE=∠ACD,
又∵∠BCE=∠BCA+∠ACE,∠ACD=∠DCE+∠ACE,
∴∠BCA=∠DCE,
在△BAC和△EDC中,
,
∴△BAC≌△EDC(AAS),
∴AC=CD,
∴∠CAE=∠D,
∵∠D=40°,
∴∠CAD=40,
∴∠ACD=180°﹣∠CAD﹣∠D=180°﹣40°﹣40°=100°,
∴∠BCE=∠ACD=100°.
故选:C.
8.解:A.∠A=∠DCE,AC=CE,∠ACB=∠E,符合全等三角形的判定定理ASA,能推出△ABC≌△CDE,故本选项不符合题意;
B.∵AB∥DE,
∴∠B=∠EDC,
∠B=∠EDC,∠ACB=∠E,AC=CE,符合全等三角形的判定定理AAS,能推出△ABC≌△CDE,故本选项不符合题意;
C.BC=DE,∠ACB=∠E,AC=CE,符合全等三角形的判定定理SAS,能推出△ABC≌△CDE,故本选项不符合题意;
D.AB=DC,AC=CE,∠ACB=∠E,不符合全等三角形的判定定理ASA,不能推出△ABC≌△CDE,故本选项符合题意;
故选:D.
9.解:∵AB=AC,
∴∠B=∠C=(180°﹣∠BAC)=(180°﹣56°)=62°,
在△BFD和△EDC中,,
∴△BFD≌△EDC(SAS),
∴∠BFD=∠EDC,
∴∠FDB+∠EDC=∠FDB+∠BFD=180°﹣∠B=180°﹣62°=118°,
则∠EDF=180°﹣(∠FDB+∠EDC)=180°﹣118°=62°.
故选:A.
10.解:如图所示:在△GDF与△BGE中,
,
∴△GDF≌△BGE(SAS).
∴S△GDF=S△BEG,
则S阴影=S△EFB=S矩形BCFE.
所以只要知道长方形BCFE的面积即可求得答案.
故选:D.
11.解:过D作BC的垂线交BC于G,过E作AD的垂线交AD的延长线于F,
∵∠EDF+∠FDC=90°,
∠GDC+∠FDC=90°,
∴∠EDF=∠GDC,
于是在Rt△EDF和Rt△CDG中,
,
∴△DEF≌△DCG,
∴EF=CG=BC﹣BG=BC﹣AD=3﹣2=1,
所以,S△ADE=(AD×EF)÷2=(2×1)÷2=1.
故选:A.
12.解:∵AB=DC,BC=BC,
∴当AC=BD(SSS)或∠ABC=∠DCB(SAS)时,
∴△ABC≌△DCB.
故答案为:AC=BD(或∠ABC=∠DCB等)
13.解:如图,延长EB至G,使BE=BG,设AC与DE交于点M,
∵∠ABC=90°,
∴AB⊥GE,
∴AB垂直平分GE,
∴AG=AE,∠GAB=∠BAE=∠DAC,
∵∠BAE=∠GAE,
∴∠GAE=∠CAD,
∴∠GAE+∠EAC=∠CAD+∠EAC,
∴∠GAC=∠EAD,
在△GAC与△EAD中,
,
∴△GAC≌△EAD(SAS),
∴∠G=∠AED,∠ACB=∠ADE,
∴②是正确的;
∵AG=AE,
∴∠G=∠AEG=∠AED,
∴AE平分∠BED,
当∠BAE=∠EAC时,∠AME=∠ABE=90°,则AC⊥DE,
当∠BAE≠∠EAC时,∠AME≠∠ABE,则无法说明AC⊥DE,
∴①是不正确的;
设∠BAE=x,则∠CAD=2x,
∴∠ACD=∠ADC==90°﹣x,
∵AB∥CD,
∴∠BAC=∠ACD=90°﹣x,
∴∠CAE=∠BAC﹣∠EAB=90°﹣x﹣x=90°﹣2x,
∴∠DAE=∠CAE+∠DAC=90°﹣2x+2x=90°,
∴AE⊥AD,
∴③是正确的;
∵△GAC≌△EAD,
∴CG=DE,
∵CG=CE+GE=CE+2BE,
∴DE=CE+2BE,
∴④是正确的,
故答案为:②③④.
14.解:∵AP是∠BAC的角平分线,
∴∠MAP=∠CAP=∠CAB=30°=15°,
∵CM⊥AP,
∴∠ANC=∠ANM=90°,
∴∠ACN=∠AMN=90°﹣15°=75°,
∵∠B=55°,
∴∠MCB=∠AMN﹣∠B=75°﹣55°=20°,
在△ACN和△AMN中,
,
∴△ACN≌△AMN(ASA),
∴CN=MN,
∴PC=PM,
∴∠PMC=∠PCM=20°,
∴∠BPM=∠PMC+∠PCM=40°.
故答案为:40°.
15.解:在△ABD与△ACE中,
∵∠1+∠CAD=∠CAE+∠CAD,
∴∠1=∠CAE;
∴,
∴△ABD≌△ACE(SAS);
∴∠2=∠ABE(对应角相等);
∵∠3=∠1+∠2,∠1=22°,∠2=28°,
∴∠3=50°.
故答案为:50.
16.解:全等,理由如下:
∵AB=AC,AD为△ABC的BC边上的中线,
∴BD=CD,
在△ABD与△ACD中,
,
∴△ABD≌△ACD(SSS).
17.证明:∵AD,AF分别是两个钝角△ABC和△ABE的高,且AD=AF,AC=AE,
∴Rt△ADC≌Rt△AFE(HL).
∴CD=EF.
∵AD=AF,AB=AB,
∴Rt△ABD≌Rt△ABF(HL).
∴BD=BF.
∴BD﹣CD=BF﹣EF.
即BC=BE.
18.(1)证明:∵CE∥DA,
∴∠ADE=∠DEC,
在△ADE和△CED中,
,
∴△ADE≌△CED(SAS),
∴CD=AE,∠A=∠DCE,
∵E为AB中点,
∴AE=BE,
∴CD=BE,
∵CE∥DA,
∴∠A=∠CEB,
∴∠DCE=∠CEB,
在△CDE和△EBC中,
,
∴△CDE≌△EBC(SAS),
∴DE=BC;
(2)解:∵CE平分∠DCB,
∴∠DCE=∠BCE,
∵∠A=∠DCE,
∴∠BCE=∠A,
∵CE∥DA,
∴∠A=∠CEB,
∴∠BCE=∠CEB,
∴BC=BE,
∵BC=6,
∴BE=6.
19.解:(1)∵AF⊥AB,
∴∠DAF=90°,
在△ADF和△BCD中,
,
∴△ADF≌△BCD(SAS),
∴DF=CD,∠ADF=∠BCD,
∵∠BCD+∠CDB=90°,
∴∠ADF+∠CDB=90°,即∠CDF=90°,
∴CD⊥DF.
故答案为:DF=CD,CD⊥DF;
(2)成立,理由如下:
∵AF⊥AB,
∴∠DAF=90°,
在△ADF和△BCD中,
,
∴△ADF≌△BCD(SAS),
∴DF=CD,∠ADF=∠BCD,
∵∠BCD+∠CDB=90°,
∴∠ADF+∠CDB=90°,即∠CDF=90°,
∴CD⊥DF;
(3)如图,由题意,过点A作AF⊥AB,并截取AF=BD,连接DF、CF,
∵∠ABC=90°,AF⊥AB,
∴AF∥CE,
∵AF=BD,CE=BD,
∴AF=CE,
∴四边形AFCE是平行四边形,
∴FC∥AE,
∴∠APD=∠FCD,
∵DF=DC,∠FDC=90°.
∴∠FCD=45°,
∴∠APC=45°.
20.解:(1)∵∠EAB=∠CAD=α,
∴∠EAC=∠BAD,
在△AEC和△ABD中,
,
∴△AEC≌△ABD(SAS),
∴∠AEC=∠ABD,
∵∠AEC+∠EAB=∠ABD+∠EMB,
∴∠EMB=∠EAB=40°;
(2)连接AG,AH,
由(1)可得:EC=BD,∠ACE=∠ADB,
∵G、H分别是EC、BD的中点,
∴DH=CG,
在△ACG和△ADH中,
,
∴△ACG≌△ADH(SAS),
∴AG=AH,∠CAG=∠DAH,
∴∠AGH=∠AHG,∠CAG﹣∠CAH=∠DAH﹣∠CAH,
∴∠GAH=∠DAC,
∵∠DAC=α,
∴∠GAH=α,
∵∠GAH+∠AHG+∠AGH=180°,
∴∠AHG=90°﹣α;
(3)如图3,连接AM,过点A作AP⊥EC于P,AN⊥BD于N,
∵△ACE≌△ADB,
∴S△ACE=S△ADB,EC=BD,
∵EC×AP=×BD×AN,
∴AP=AN,
又∵AP⊥EC,AN⊥BD,
∴∠AME=∠AMD=,
∴∠AMC=∠AMD+∠DMC=90°+α,
故答案为:90°+α.
21.解:(1)∵BD⊥AC,CF⊥AB,
∴∠DCE+∠DEC=∠DCE+∠FAC=90°,
∴∠DEC=∠BAC,∠DEC+∠BEC=180°,
∴∠BAC+∠BEC=180°;
(2)∵BD平分∠ABC,CF平分∠ACB,
∴∠EBC=ABC,∠ECB=ACB,∠BEC=180°﹣(∠EBC+∠ECB)=180°﹣(∠ABC+∠ACB)=180°﹣(180°﹣∠BAC)=90°∠BAC;
(3)作∠BEC的平分线EM交BC于M,
∵∠BAC=60°,
∴∠BEC=90°+BAC=120°,
∴∠FEB=∠DEC=60°,
∵EM平分∠BEC,
∴∠BEM=60°,
在△FBE与△EBM中,
,
∴△FBE≌△EBM(ASA),
∴EF=EM,同理DE=EM,
∴EF=DE.
22.(1)证明:在△ABC和△EDC中,
,
∴△ABC≌△EDC(SAS),
∴∠A=∠E,
∴AB∥DE;
(2)当0≤t≤2时,BP=(6﹣3t)
cm,
当2<t≤4时,BP=(3t﹣6)cm,
综上所述,线段BP的长为(6﹣3t)
cm或(3t﹣6)cm;
(3)由(1)得:∠A=∠E,ED=AB=4cm,
在△ACP和△ECQ中,
,
∴△ACP≌△ECQ(ASA),
∴AP=EQ,
当0≤t≤2时,3t=6﹣t,
解得:t=1.5;
当2<t≤4时,12﹣3t=6﹣t,
解得:t=3;
综上所述,当线段PQ经过点C时,t的值为1.5s或3s.
1.如图,方格中△ABC的三个顶点分别在正方形的顶点(格点上),这样的三角形叫格点三角形,图中可以画出与△ABC全等的格点三角形共有( )个.(不含△ABC)
A.28
B.29
C.30
D.31
2.如图,AD是△ABC的角平分线,∠C=2∠B,F是BC的中点,EF∥AD交AB于点E,且BE=4AE,若CD=4,则AB的长为( )
A.10
B.9
C.8
D.6
3.如图,∠ACB=90°,AC=CD,过点D作AB的垂线交AB的延长线于点E.若AB=2DE,则∠BAC的度数为( )
A.45°
B.30°
C.22.5°
D.15°
4.如图,在△ABC和△DEF中,点B、F、C、D在同一条直线上,已知∠A=∠D,AB=DE,添加以下条件,不能判定△ABC≌△DEF的是( )
A.∠B=∠E
B.AC=DF
C.∠ACD=∠BFE
D.BF=CD
5.如图,E是△ABC的边AC的中点,过点C作CF∥AB,过点E作直线DF交AB于D,交CF于F,若AB=9,CF=6.5,则BD的长为( )
A.1
B.2
C.2.5
D.3
6.打碎的一块三角形玻璃如图所示,现在要去玻璃店配一块完全一样的玻璃,最省事的方法是( )
A.带①②去
B.带②③去
C.带③④去
D.带②④去
7.如图,在四边形ABCD中,点E在边AD上,∠BCE=∠ACD,∠BAC=∠D=40°,AB=DE,则∠BCE的度数为( )
A.80°
B.90°
C.100°
D.110°
8.如图,在△ABC和△CDE中,点B、D、C在同一直线上,已知∠ACB=∠E,AC=CE,添加以下条件后,仍不能判定△ABC≌△CDE的是( )
A.∠A=∠DCE
B.AB∥DE
C.BC=DE
D.AB=CD
9.如图,D为△ABC边BC上一点,AB=AC,∠BAC=56°,且BF=DC,EC=BD,则∠EDF等于( )
A.62°
B.56°
C.34°
D.124°
10.如图,正方形ABCD被分割成2个长方形和1个正方形,要求图中阴影部分的面积,只要知道下列图形的面积是( )
A.长方形AEFD
B.长方形BEGH
C.正方形CFGH
D.长方形BCFE
11.已知如图,AD∥BC,AB⊥BC,CD⊥DE,CD=ED,AD=2,BC=3,则△ADE的面积为( )
A.1
B.2
C.5
D.无法确定
12.如图,AC与BD交于O点,若AB=DC,请补充一个条件:
,使△ABC≌△DCB.
13.如图,在Rt△ABC中,∠ABC=90°,以AC为边,作△ACD,满足AD=AC,点E为BC上一点,连接AE,∠BAE=∠CAD,连接DE.下列结论中正确的是
.(填序号)
①AC⊥DE;
②∠ADE=∠ACB;
③若CD∥AB,则AE⊥AD;
④DE=CE+2BE.
14.如图,在△ABC中,过点A作∠BAC的角平分线交BC于P,CM⊥AP于N.若∠CAB=30°,∠B=55°,则∠BPM=
.
15.如图,D在线段BE上一点,AB=AC,AD=AE,∠BAC=∠DAE,∠1=22°,∠2=28°,∠3=
°.
16.如图,AB=AC,AD为△ABC的BC边上的中线,△ABD与△ACD全等吗?为什么?
17.如图,已知AD,AF分别是两个钝角△ABC和△ABE的高,如果AD=AF,AC=AE.
求证:BC=BE.
18.如图,E为AB中点,CE=DA,CE∥DA.
(1)求证:DE=BC;
(2)若∠A=∠DCE,CE平分∠DCB,BC=6,求BE的长.
19.如图1,∠ABC=90°,FA⊥AB于点A,D是线段AB上的点,AD=BC,AF=BD.
(1)判断DF与DC的数量关系为
,位置关系为
.
(2)如图2,若点D在线段AB的延长线上,过点A在AB的另一侧作AF⊥AB,并截取AF=BD,连接DC、DF、CF,试说明(1)中结论是否成立,并说明理由.
(3)若点D在线段AB外(线段AB所在的直线上且除线段AB),点E是BC延长线上一点,且CE=BD,连接AE,与DC的延长线交于点P,直接写出∠APC的度数.
20.以△ABC的AB、AC为边作△ABD和△ACE,且AE=AB,AC=AD,CE与BD相交于M,∠EAB=∠CAD=α.
(1)如图1,若α=40°,求∠EMB的度数;
(2)如图2,若G、H分别是EC、BD的中点,求∠AHG的度数(用含α式子表示);
(3)如图3,连接AM,直接写出∠AMC与α的数量关系是
.
21.已知△ABC,点D、F分别为线段AC、AB上两点,连接BD、CF交于点E.
(1)若BD⊥AC,CF⊥AB,如图1所示,试说明∠BAC+∠BEC=180°;
(2)若BD平分∠ABC,CF平分∠ACB,如图2所示,试说明此时∠BAC与∠BEC的数量关系;
(3)在(2)的条件下,若∠BAC=60°,试说明:EF=ED.
22.如图,AE与BD相交于点C,AC=EC,BC=DC,AB=6cm,点P从点A出发,沿A→B→A方向以3cm/s的速度运动,点Q从点D出发,沿D→E方向以1cm/s的速度运动,P、Q两点同时出发.当点P到达点A时,P、Q两点同时停止运动.设点P的运动时间为t(s).
(1)求证:AB∥DE.
(2)写出线段BP的长(用含t的式子表示).
(3)连接PQ,当线段PQ经过点C时,求t的值.
参考答案
1.解:当点B在下面时,根据平移,对称,可得与△ABC全等的三角形有8个,包括△ABC,
当点B在其它3条边上时,有3×8=24(个)三角形与△ABC全等,
∴一共有:8+24﹣1=31(个)三角形与△ABC全等,
故选:D.
2.解:如图作DG⊥AC于G,DH⊥AB于H,在AB上截取AM=AC,
∵DA平分∠BAC,
∴DG=DH,
∴===,
设BF=FC=4a,
∵EF∥AD,
∴FD=a,CD=3a=4,
∴a=,BD=5a=,
在△ADM和△ADC中,
,
∴△DAM≌△DAC(SAS),
∴DM=DC,∠AMD=∠C,
∵∠C=2∠B,
∴∠AMD=∠B+∠MDB=2∠B,
∴∠B=∠MDB,
∴BM=MD=CD=4,设AC=AM=x,
∴x=6,
∴AB=BM+AC=4+6=10,
故选:A.
3.解:连接AD,延长AC、DE交于M,
∵∠ACB=90°,AC=CD,
∴∠DAC=∠ADC=45°,
∵∠ACB=90°,DE⊥AB,
∴∠DEB=90°=∠ACB=∠DCM,
∵∠ABC=∠DBE,
∴由三角形内角和定理得:∠CAB=∠CDM,
在△ACB和△DCM中
∴△ACB≌△DCM(ASA),
∴AB=DM,
∵AB=2DE,
∴DM=2DE,
∴DE=EM,
∵DE⊥AB,
∴AD=AM,
∴∠BAC=∠DAE=∠DAC==22.5°,
故选:C.
4.解:A.符合全等三角形的判定定理ASA,能推出△ABC≌△DEF,故本选项不符合题意;
B.符合全等三角形的判定定理SAS,能推出△ABC≌△DEF,故本选项不符合题意;
C.∵∠ACD=∠BFE,∠ACD=∠A+∠ABC,∠BFE=∠E+∠D,∠A=∠D,
∴∠B=∠E,
即符合全等三角形的判定定理ASA,能推出△ABC≌△DEF,故本选项不符合题意;
D.∵BF=CD,
∴BF+CF=CD+CF,
即BC=DF,
∵∠A=∠D,AB=DE,
∴不符合全等三角形的判定定理,不能推出△ABC≌△DEF,故本选项符合题意;
故选:D.
5.证明:∵CF∥AB,
∴∠1=∠F,∠2=∠A,
∵点E为AC的中点,
∴AE=EC,
在△ADE和△CFE中
,
∴△ADE≌△CFE(AAS),
∴AD=CF=6.5,
∵AB=9,
∴BD=AB﹣AD=9﹣6.5=2.5,
故选:C.
6.解:A、带①②去,符合ASA判定,选项符合题意;
B、带②③去,仅保留了原三角形的一个角和部分边,不符合任何判定方法,选项不符合题意;
C、带③④去,仅保留了原三角形的一个角和部分边,不符合任何判定方法,选项不符合题意;
D、带②④去,仅保留了原三角形的两个角和部分边,不符合任何判定方法,选项不符合题意;
故选:A.
7.解:∵∠BCE=∠ACD,
又∵∠BCE=∠BCA+∠ACE,∠ACD=∠DCE+∠ACE,
∴∠BCA=∠DCE,
在△BAC和△EDC中,
,
∴△BAC≌△EDC(AAS),
∴AC=CD,
∴∠CAE=∠D,
∵∠D=40°,
∴∠CAD=40,
∴∠ACD=180°﹣∠CAD﹣∠D=180°﹣40°﹣40°=100°,
∴∠BCE=∠ACD=100°.
故选:C.
8.解:A.∠A=∠DCE,AC=CE,∠ACB=∠E,符合全等三角形的判定定理ASA,能推出△ABC≌△CDE,故本选项不符合题意;
B.∵AB∥DE,
∴∠B=∠EDC,
∠B=∠EDC,∠ACB=∠E,AC=CE,符合全等三角形的判定定理AAS,能推出△ABC≌△CDE,故本选项不符合题意;
C.BC=DE,∠ACB=∠E,AC=CE,符合全等三角形的判定定理SAS,能推出△ABC≌△CDE,故本选项不符合题意;
D.AB=DC,AC=CE,∠ACB=∠E,不符合全等三角形的判定定理ASA,不能推出△ABC≌△CDE,故本选项符合题意;
故选:D.
9.解:∵AB=AC,
∴∠B=∠C=(180°﹣∠BAC)=(180°﹣56°)=62°,
在△BFD和△EDC中,,
∴△BFD≌△EDC(SAS),
∴∠BFD=∠EDC,
∴∠FDB+∠EDC=∠FDB+∠BFD=180°﹣∠B=180°﹣62°=118°,
则∠EDF=180°﹣(∠FDB+∠EDC)=180°﹣118°=62°.
故选:A.
10.解:如图所示:在△GDF与△BGE中,
,
∴△GDF≌△BGE(SAS).
∴S△GDF=S△BEG,
则S阴影=S△EFB=S矩形BCFE.
所以只要知道长方形BCFE的面积即可求得答案.
故选:D.
11.解:过D作BC的垂线交BC于G,过E作AD的垂线交AD的延长线于F,
∵∠EDF+∠FDC=90°,
∠GDC+∠FDC=90°,
∴∠EDF=∠GDC,
于是在Rt△EDF和Rt△CDG中,
,
∴△DEF≌△DCG,
∴EF=CG=BC﹣BG=BC﹣AD=3﹣2=1,
所以,S△ADE=(AD×EF)÷2=(2×1)÷2=1.
故选:A.
12.解:∵AB=DC,BC=BC,
∴当AC=BD(SSS)或∠ABC=∠DCB(SAS)时,
∴△ABC≌△DCB.
故答案为:AC=BD(或∠ABC=∠DCB等)
13.解:如图,延长EB至G,使BE=BG,设AC与DE交于点M,
∵∠ABC=90°,
∴AB⊥GE,
∴AB垂直平分GE,
∴AG=AE,∠GAB=∠BAE=∠DAC,
∵∠BAE=∠GAE,
∴∠GAE=∠CAD,
∴∠GAE+∠EAC=∠CAD+∠EAC,
∴∠GAC=∠EAD,
在△GAC与△EAD中,
,
∴△GAC≌△EAD(SAS),
∴∠G=∠AED,∠ACB=∠ADE,
∴②是正确的;
∵AG=AE,
∴∠G=∠AEG=∠AED,
∴AE平分∠BED,
当∠BAE=∠EAC时,∠AME=∠ABE=90°,则AC⊥DE,
当∠BAE≠∠EAC时,∠AME≠∠ABE,则无法说明AC⊥DE,
∴①是不正确的;
设∠BAE=x,则∠CAD=2x,
∴∠ACD=∠ADC==90°﹣x,
∵AB∥CD,
∴∠BAC=∠ACD=90°﹣x,
∴∠CAE=∠BAC﹣∠EAB=90°﹣x﹣x=90°﹣2x,
∴∠DAE=∠CAE+∠DAC=90°﹣2x+2x=90°,
∴AE⊥AD,
∴③是正确的;
∵△GAC≌△EAD,
∴CG=DE,
∵CG=CE+GE=CE+2BE,
∴DE=CE+2BE,
∴④是正确的,
故答案为:②③④.
14.解:∵AP是∠BAC的角平分线,
∴∠MAP=∠CAP=∠CAB=30°=15°,
∵CM⊥AP,
∴∠ANC=∠ANM=90°,
∴∠ACN=∠AMN=90°﹣15°=75°,
∵∠B=55°,
∴∠MCB=∠AMN﹣∠B=75°﹣55°=20°,
在△ACN和△AMN中,
,
∴△ACN≌△AMN(ASA),
∴CN=MN,
∴PC=PM,
∴∠PMC=∠PCM=20°,
∴∠BPM=∠PMC+∠PCM=40°.
故答案为:40°.
15.解:在△ABD与△ACE中,
∵∠1+∠CAD=∠CAE+∠CAD,
∴∠1=∠CAE;
∴,
∴△ABD≌△ACE(SAS);
∴∠2=∠ABE(对应角相等);
∵∠3=∠1+∠2,∠1=22°,∠2=28°,
∴∠3=50°.
故答案为:50.
16.解:全等,理由如下:
∵AB=AC,AD为△ABC的BC边上的中线,
∴BD=CD,
在△ABD与△ACD中,
,
∴△ABD≌△ACD(SSS).
17.证明:∵AD,AF分别是两个钝角△ABC和△ABE的高,且AD=AF,AC=AE,
∴Rt△ADC≌Rt△AFE(HL).
∴CD=EF.
∵AD=AF,AB=AB,
∴Rt△ABD≌Rt△ABF(HL).
∴BD=BF.
∴BD﹣CD=BF﹣EF.
即BC=BE.
18.(1)证明:∵CE∥DA,
∴∠ADE=∠DEC,
在△ADE和△CED中,
,
∴△ADE≌△CED(SAS),
∴CD=AE,∠A=∠DCE,
∵E为AB中点,
∴AE=BE,
∴CD=BE,
∵CE∥DA,
∴∠A=∠CEB,
∴∠DCE=∠CEB,
在△CDE和△EBC中,
,
∴△CDE≌△EBC(SAS),
∴DE=BC;
(2)解:∵CE平分∠DCB,
∴∠DCE=∠BCE,
∵∠A=∠DCE,
∴∠BCE=∠A,
∵CE∥DA,
∴∠A=∠CEB,
∴∠BCE=∠CEB,
∴BC=BE,
∵BC=6,
∴BE=6.
19.解:(1)∵AF⊥AB,
∴∠DAF=90°,
在△ADF和△BCD中,
,
∴△ADF≌△BCD(SAS),
∴DF=CD,∠ADF=∠BCD,
∵∠BCD+∠CDB=90°,
∴∠ADF+∠CDB=90°,即∠CDF=90°,
∴CD⊥DF.
故答案为:DF=CD,CD⊥DF;
(2)成立,理由如下:
∵AF⊥AB,
∴∠DAF=90°,
在△ADF和△BCD中,
,
∴△ADF≌△BCD(SAS),
∴DF=CD,∠ADF=∠BCD,
∵∠BCD+∠CDB=90°,
∴∠ADF+∠CDB=90°,即∠CDF=90°,
∴CD⊥DF;
(3)如图,由题意,过点A作AF⊥AB,并截取AF=BD,连接DF、CF,
∵∠ABC=90°,AF⊥AB,
∴AF∥CE,
∵AF=BD,CE=BD,
∴AF=CE,
∴四边形AFCE是平行四边形,
∴FC∥AE,
∴∠APD=∠FCD,
∵DF=DC,∠FDC=90°.
∴∠FCD=45°,
∴∠APC=45°.
20.解:(1)∵∠EAB=∠CAD=α,
∴∠EAC=∠BAD,
在△AEC和△ABD中,
,
∴△AEC≌△ABD(SAS),
∴∠AEC=∠ABD,
∵∠AEC+∠EAB=∠ABD+∠EMB,
∴∠EMB=∠EAB=40°;
(2)连接AG,AH,
由(1)可得:EC=BD,∠ACE=∠ADB,
∵G、H分别是EC、BD的中点,
∴DH=CG,
在△ACG和△ADH中,
,
∴△ACG≌△ADH(SAS),
∴AG=AH,∠CAG=∠DAH,
∴∠AGH=∠AHG,∠CAG﹣∠CAH=∠DAH﹣∠CAH,
∴∠GAH=∠DAC,
∵∠DAC=α,
∴∠GAH=α,
∵∠GAH+∠AHG+∠AGH=180°,
∴∠AHG=90°﹣α;
(3)如图3,连接AM,过点A作AP⊥EC于P,AN⊥BD于N,
∵△ACE≌△ADB,
∴S△ACE=S△ADB,EC=BD,
∵EC×AP=×BD×AN,
∴AP=AN,
又∵AP⊥EC,AN⊥BD,
∴∠AME=∠AMD=,
∴∠AMC=∠AMD+∠DMC=90°+α,
故答案为:90°+α.
21.解:(1)∵BD⊥AC,CF⊥AB,
∴∠DCE+∠DEC=∠DCE+∠FAC=90°,
∴∠DEC=∠BAC,∠DEC+∠BEC=180°,
∴∠BAC+∠BEC=180°;
(2)∵BD平分∠ABC,CF平分∠ACB,
∴∠EBC=ABC,∠ECB=ACB,∠BEC=180°﹣(∠EBC+∠ECB)=180°﹣(∠ABC+∠ACB)=180°﹣(180°﹣∠BAC)=90°∠BAC;
(3)作∠BEC的平分线EM交BC于M,
∵∠BAC=60°,
∴∠BEC=90°+BAC=120°,
∴∠FEB=∠DEC=60°,
∵EM平分∠BEC,
∴∠BEM=60°,
在△FBE与△EBM中,
,
∴△FBE≌△EBM(ASA),
∴EF=EM,同理DE=EM,
∴EF=DE.
22.(1)证明:在△ABC和△EDC中,
,
∴△ABC≌△EDC(SAS),
∴∠A=∠E,
∴AB∥DE;
(2)当0≤t≤2时,BP=(6﹣3t)
cm,
当2<t≤4时,BP=(3t﹣6)cm,
综上所述,线段BP的长为(6﹣3t)
cm或(3t﹣6)cm;
(3)由(1)得:∠A=∠E,ED=AB=4cm,
在△ACP和△ECQ中,
,
∴△ACP≌△ECQ(ASA),
∴AP=EQ,
当0≤t≤2时,3t=6﹣t,
解得:t=1.5;
当2<t≤4时,12﹣3t=6﹣t,
解得:t=3;
综上所述,当线段PQ经过点C时,t的值为1.5s或3s.
