2019-2020学年湖南省张家界市永定区八年级(上)期中数学试卷(Word版 含解析)
文档属性
| 名称 | 2019-2020学年湖南省张家界市永定区八年级(上)期中数学试卷(Word版 含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 635.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-20 06:38:02 | ||
图片预览




文档简介
2019-2020学年湖南省张家界市永定区八年级第一学期期中数学试卷
一、选择题(本大题共8个小题,每小题3分,满分24分.请将正确答案的字母代号填在下表中.)
1.下列代数式,不是分式的是( )
A.
B.
C.
D.
2.已知三角形的两边长分别是4和8,那么这个三角形第三边长可能是( )
A.2
B.4
C.9
D.13
3.若代数式有意义,则实数x的取值范围是( )
A.x=0
B.x=3
C.x≠0
D.x≠3
4.下列计算正确的是( )
A.(﹣1)﹣1=1
B.(﹣1)0=0
C.|﹣1|=﹣1
D.﹣(﹣1)﹣1=1
5.下列各图中,正确画出AC边上的高的是( )
A.
B.
C.
D.
6.如图,在△ABC中,点D在BC上,AB=AD=DC,∠B=80°,则∠C的度数为( )
A.30°
B.40°
C.45°
D.60°
7.下列计算正确的有几个( )
=﹣1;=﹣1;=x+y;=2.
A.4个
B.3个
C.2个
D.1个
8.下列命题的逆命题一定成立的是( )
①对顶角相等;
②同位角相等,两直线平行;
③全等三角形的周长相等;
④能够完全重合的两个三角形全等.
A.①②③
B.①④
C.②④
D.②
二、填空题(共6小题,每小题3分,满分18分)
9.如果分式的值为零,那么x=
.
10.医学家发现了一种病毒,其长度约为0.00000029mm,用科学记数法表示为
mm.
11.如图,等腰三角形ABC中,AB=AC,∠A=44°,CD⊥AB于D,则∠DCB等于
.
12.若解分式方程产生增根,则m=
.
13.如图,在△ABC中,∠ABC=116°,若DE、FG分别垂直平分AB、BC,那么∠EBF的度数为
度.
14.观察下列各等式:,,,…根据你发现的规律,计算:=
(n为正整数).
三、解答题(本大题共9道小题,合计58分)
15.(1);
(2)+.
16.解方程:﹣=1.
17.先化简,然后从0,1,2,3中选取一个你认为符合题意的x的值代入求值.
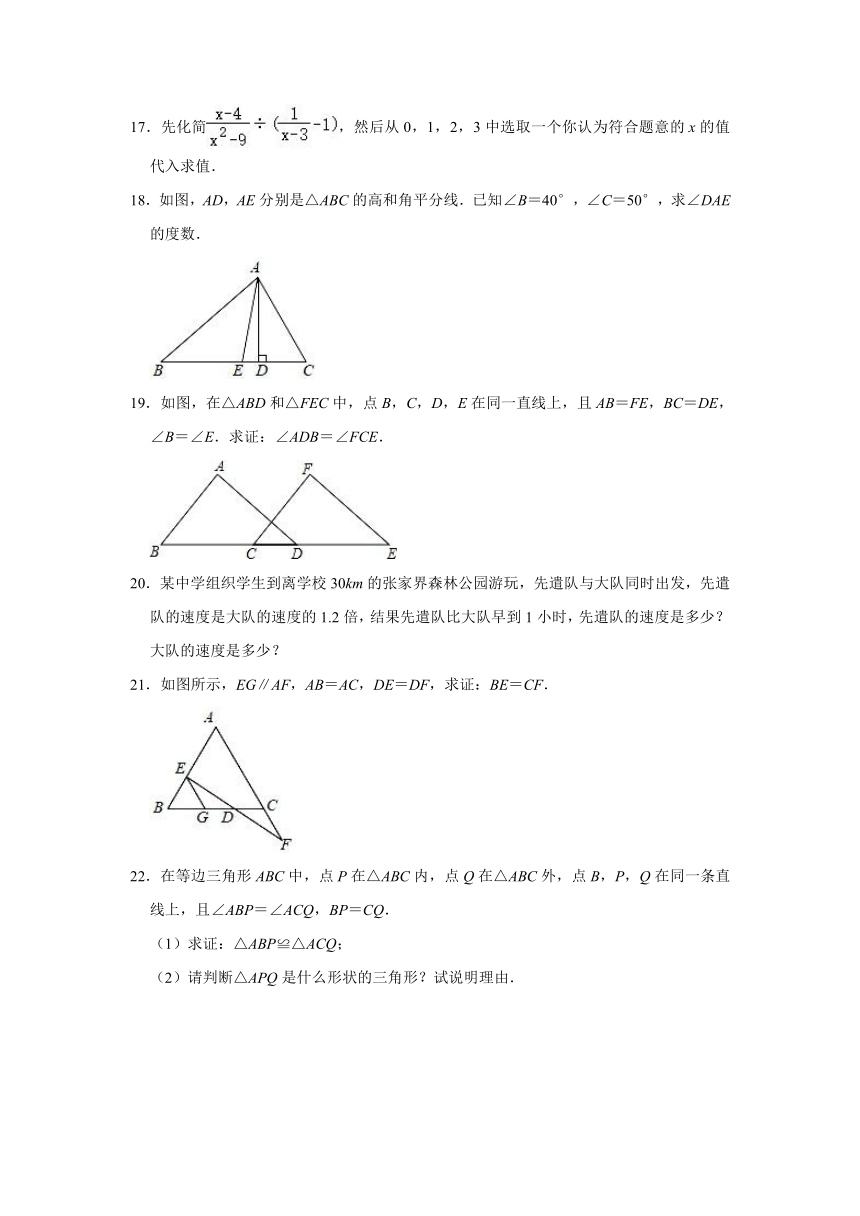
18.如图,AD,AE分别是△ABC的高和角平分线.已知∠B=40°,∠C=50°,求∠DAE的度数.
19.如图,在△ABD和△FEC中,点B,C,D,E在同一直线上,且AB=FE,BC=DE,∠B=∠E.求证:∠ADB=∠FCE.
20.某中学组织学生到离学校30km的张家界森林公园游玩,先遣队与大队同时出发,先遣队的速度是大队的速度的1.2倍,结果先遣队比大队早到1小时,先遣队的速度是多少?大队的速度是多少?
21.如图所示,EG∥AF,AB=AC,DE=DF,求证:BE=CF.
22.在等边三角形ABC中,点P在△ABC内,点Q在△ABC外,点B,P,Q在同一条直线上,且∠ABP=∠ACQ,BP=CQ.
(1)求证:△ABP≌△ACQ;
(2)请判断△APQ是什么形状的三角形?试说明理由.
23.如图,在△ABC中,∠ACB=90°,以AC为边在△ABC外作等边三角形ACD,过点D作AC的垂线,垂足为F,延长DF交AB于点E,连接CE.
(1)求证:CE=BE.
(2)若AB=15cm,P是直线DE上的一点.则当P在何处时,PB+PC最小?并求出此时PB+PC的值.
参考答案
一、选择题(本大题共8个小题,每小题3分,满分24分.请将正确答案的字母代号填在下表中.)
1.下列代数式,不是分式的是( )
A.
B.
C.
D.
【分析】根据分式的定义判断即可.
解:一般地,如果A,B表示两个整式,并且B中含有字母,那么式子叫做分式,
∴不是分式,
故选:A.
2.已知三角形的两边长分别是4和8,那么这个三角形第三边长可能是( )
A.2
B.4
C.9
D.13
【分析】根据三角形的三边关系可得8﹣4<x<8+4,解不等式,确定x的取值范围,然后可得答案.
解:设第三边长为x,由题意得:8﹣4<x<8+4,
即4<x<12,
故选:C.
3.若代数式有意义,则实数x的取值范围是( )
A.x=0
B.x=3
C.x≠0
D.x≠3
【分析】根据分式有意义的条件列出不等式解不等式即可.
解:由题意得,x﹣3≠0,
解得,x≠3,
故选:D.
4.下列计算正确的是( )
A.(﹣1)﹣1=1
B.(﹣1)0=0
C.|﹣1|=﹣1
D.﹣(﹣1)﹣1=1
【分析】根据负整数指数幂计算A,D选项,根据零指数幂计算B选项,根据绝对值的性质计算C选项.
解:A选项,原式==﹣1,故该选项不符合题意;
B选项,(﹣1)0=1,故该选项不符合题意;
C选项,|﹣1|=1,故该选项不符合题意;
D选项,﹣(﹣1)﹣1=﹣=1,故该选项符合题意;
故选:D.
5.下列各图中,正确画出AC边上的高的是( )
A.
B.
C.
D.
【分析】根据三角形高的定义,过点B与AC边垂直,且垂足在边AC上,然后结合各选项图形解答.
解:根据三角形高线的定义,只有D选项中的BE是边AC上的高.
故选:D.
6.如图,在△ABC中,点D在BC上,AB=AD=DC,∠B=80°,则∠C的度数为( )
A.30°
B.40°
C.45°
D.60°
【分析】先根据等腰三角形的性质求出∠ADB的度数,再由平角的定义得出∠ADC的度数,根据等腰三角形的性质即可得出结论.
解:∵△ABD中,AB=AD,∠B=80°,
∴∠B=∠ADB=80°,
∴∠ADC=180°﹣∠ADB=100°,
∵AD=CD,
∴∠C===40°.
故选:B.
7.下列计算正确的有几个( )
=﹣1;=﹣1;=x+y;=2.
A.4个
B.3个
C.2个
D.1个
【分析】根据分式的基本性质判断即可.
解:根据分式的基本性质,知道前三个都不正确,
=
=
=2,
综上,正确的有1个,
故选:D.
8.下列命题的逆命题一定成立的是( )
①对顶角相等;
②同位角相等,两直线平行;
③全等三角形的周长相等;
④能够完全重合的两个三角形全等.
A.①②③
B.①④
C.②④
D.②
【分析】写出原命题的逆命题后判断正误即可.
解:①对顶角相等的逆命题为相等的角为对顶角,不成立,不符合题意;
②同位角相等,两直线平行的逆命题为两直线平行,同位角相等,成立,符合题意;
③全等三角形的周长相等的逆命题为周长相等的三角形全等,不成立,不符合题意;
④能够完全重合的两个三角形全等的逆命题为全等三角形能够完全重合,成立,符合题意,
故选:C.
二、填空题(共6小题,每小题3分,满分18分)
9.如果分式的值为零,那么x= ﹣1 .
【分析】分式的值为0的条件是:分子为0,分母不为0,两个条件需同时具备,缺一不可.据此可以解答本题.
解:如果分式的值为零,则|x|﹣1=0.
解得x=1或﹣1.
x﹣1≠0,解得x≠1,
∴x=﹣1.
故答案为﹣1.
10.医学家发现了一种病毒,其长度约为0.00000029mm,用科学记数法表示为 2.9×10﹣7 mm.
【分析】绝对值小于1的正数也可以利用科学记数法表示,一般形式为a×10﹣n,与较大数的科学记数法不同的是其所使用的是负指数幂,指数由原数左边起第一个不为零的数字前面的0的个数所决定.
解:0.00000029=2.9×10﹣7,
故答案为:2.9×10﹣7.
11.如图,等腰三角形ABC中,AB=AC,∠A=44°,CD⊥AB于D,则∠DCB等于 22° .
【分析】由等腰三角形ABC中,AB=AC,∠A=44°,根据等边对等角的性质,即可求得∠ACB的度数,又由CD⊥AB,可求得∠ACD的度数,继而求得答案.
解:∵等腰三角形ABC中,AB=AC,∠A=44°,
∴∠ACB=∠B==68°,
∵CD⊥AB,
∴∠ACD=90°﹣∠A=46°,
∴∠DCB=∠ACB﹣∠ACD=68°﹣46°=22°.
故答案为:22°.
12.若解分式方程产生增根,则m= ﹣5 .
【分析】分式方程去分母后转化为整式方程,由分式方程无解得到x=﹣4,代入整式方程即可求出m的值.
解:方程去分母得:x﹣1=m,
由题意将x=﹣4代入方程得:﹣4﹣1=m,
解得:m=﹣5.
故答案为:﹣5.
13.如图,在△ABC中,∠ABC=116°,若DE、FG分别垂直平分AB、BC,那么∠EBF的度数为
52 度.
【分析】根据三角形内角和定理求出∠A+∠C,根据线段垂直平分线的性质得到EA=EB,FB=FC,进而得出∠EBA=∠A,∠FBC=∠C,结合图形计算,得到答案.
解:在△ABC中,∠ABC=116°,
则∠A+∠C=180°﹣116°=64°,
∵DE、FG分别垂直平分AB、BC,
∴EA=EB,FB=FC,
∴∠EBA=∠A,∠FBC=∠C,
∴∠EBA+∠FBC=∠A+∠C=64°,
∴∠EBF=116°﹣64°=52°,
故答案为:52.
14.观察下列各等式:,,,…根据你发现的规律,计算:= (n为正整数).
【分析】根据题目中给出的等式,先对所求式子提出公因数2019,然后将括号内的式子分解,再加减即可.
解:
=2019×[+++…+]
=2019×(1﹣+++…+)
=2019×(1﹣)
=2019×
=,
故答案为:.
三、解答题(本大题共9道小题,合计58分)
15.(1);
(2)+.
【分析】(1)先化简有理数的乘方,零指数幂,负整数指数幂,然后再计算;
(2)先通分,然后按照同分母分式加法运算法则进行计算.
解:(1)原式=﹣(﹣1)﹣1+4
=1﹣1+4
=4;
(2)原式=+
=
=
=.
16.解方程:﹣=1.
【分析】分式方程去分母转化为整式方程,求出整式方程的解得到x的值,经检验即可得到分式方程的解.
解:去分母得:x(x+2)﹣2=x2﹣4,
去括号得:x2+2x﹣2=x2﹣4,
解得:x=﹣1,
经检验x=﹣1是分式方程的解.
17.先化简,然后从0,1,2,3中选取一个你认为符合题意的x的值代入求值.
【分析】根据分式的减法和除法可以化简题目中的式子,然后从0,1,2,3中选取一个使得原分式有意义的值代入化简后的式子即可解答本题.
解:
=÷
=
=﹣,
∵(x+3)(x﹣3)≠0,4﹣x≠0,
∴x≠±3,4,
∴x=0,1,2,
当x=0时,原式=﹣=﹣.
18.如图,AD,AE分别是△ABC的高和角平分线.已知∠B=40°,∠C=50°,求∠DAE的度数.
【分析】根据三角形的内角和可求解∠BAC的度数,结合角平分线的定义可求解∠BAE的度数,由三角形高线可求解∠BAD的度数,进而可求解.
解:(1)∵∠B=40°,∠C=50°,
∴∠BAC=180°﹣∠B﹣∠C=180°﹣40°﹣50°=90°,
∵AE是角平分线,
∴∠BAE=∠BAC=×90°=45°,
∵AD是△ABC的高,
∴∠BAD=90°﹣∠B=90°﹣40°=50°,
∴∠DAE=∠BAD﹣∠BAE=50°﹣45°=5°.
19.如图,在△ABD和△FEC中,点B,C,D,E在同一直线上,且AB=FE,BC=DE,∠B=∠E.求证:∠ADB=∠FCE.
【分析】根据等式的性质得出BD=CE,再利用SAS得出:△ABD与△FEC全等,进而得出∠ADB=∠FCE.
【解答】证明:∵BC=DE,
∴BC+CD=DE+CD,
即BD=CE,
在△ABD与△FEC中,
,
∴△ABD≌△FEC(SAS),
∴∠ADB=∠FCE.
20.某中学组织学生到离学校30km的张家界森林公园游玩,先遣队与大队同时出发,先遣队的速度是大队的速度的1.2倍,结果先遣队比大队早到1小时,先遣队的速度是多少?大队的速度是多少?
【分析】设大队的速度为xkm/h,则先遣队的速度是1.2xkm/h,利用时间=路程÷速度,结合先遣队比大队早到1小时,即可得出关于x的分式方程,解之经检验后即可得出大队的速度,再将其代入1.2x中可求出先遣队的速度.
解:设大队的速度为xkm/h,则先遣队的速度是1.2xkm/h,
依题意得:﹣=1,
解得:x=5,
经检验,x=5是原分式方程的解且符合实际,
∴1.2x=1.2×5=6.
答:先遣队的速度是6km/h,大队的速度是5km/h.
21.如图所示,EG∥AF,AB=AC,DE=DF,求证:BE=CF.
【分析】由平行线的性质得出∠GED=∠F,∠BGE=∠BCA,证出BE=EG,证明△DEG≌△DFC(ASA),由全等三角形的性质可得出EG=CF,则可得出结论.
【解答】证明:∵EG∥AF,
∴∠GED=∠F,∠BGE=∠BCA,
∵AB=AC,
∴∠B=∠BCA,
∴∠B=∠BGE,
∴BE=EG.
在△DEG和△DFC中,
,
∴△DEG≌△DFC(ASA),
∴EG=CF,
∴BE=CF.
22.在等边三角形ABC中,点P在△ABC内,点Q在△ABC外,点B,P,Q在同一条直线上,且∠ABP=∠ACQ,BP=CQ.
(1)求证:△ABP≌△ACQ;
(2)请判断△APQ是什么形状的三角形?试说明理由.
【分析】(1)根据等边三角形的性质可得AB=AC,再根据SAS证明△ABP≌△ACQ;
(2)根据全等三角形的性质得到AP=AQ,再证∠PAQ=60°,从而得出△APQ是等边三角形.
【解答】证明:(1)∵△ABC为等边三角形,
∴AB=AC,∠BAC=60°,
在△ABP和△ACQ中,
,
∴△ABP≌△ACQ(SAS),
(2)∵△ABP≌△ACQ,
∴∠BAP=∠CAQ,AP=AQ,
∵∠BAP+∠CAP=60°,
∴∠PAQ=∠CAQ+∠CAP=60°,
∴△APQ是等边三角形.
23.如图,在△ABC中,∠ACB=90°,以AC为边在△ABC外作等边三角形ACD,过点D作AC的垂线,垂足为F,延长DF交AB于点E,连接CE.
(1)求证:CE=BE.
(2)若AB=15cm,P是直线DE上的一点.则当P在何处时,PB+PC最小?并求出此时PB+PC的值.
【分析】(1)先证明DE是AC的垂直平分线,再证明DE∥BC,最后由∠ECB=∠EBC,即可证得CE=BE;
(2)连接PA,PC,由垂直平分线的性质可得PC=PA,再由两点之间线段最短即可得到所求PA+PB最小为AB的长.
解:(1)∵△ACD为等边三角形,DE⊥AC,
∴DE垂直平分AC,
∴∠AEF=∠FEC,
∵∠ACB=∠AFE=90°,
∴DE∥BC,
∴∠AEF=∠EBC,∠FEC=∠ECB,
∴∠ECB=∠EBC,
∴CE=BE;
(2)连接PA,PC,
∵DE垂直平分AC,P在DE上,
∴PC=PA,
∵两点之间线段最短,
∴当P与E重合时PA+PB最小为15
cm,
∴PB+PC最小为15
cm.
一、选择题(本大题共8个小题,每小题3分,满分24分.请将正确答案的字母代号填在下表中.)
1.下列代数式,不是分式的是( )
A.
B.
C.
D.
2.已知三角形的两边长分别是4和8,那么这个三角形第三边长可能是( )
A.2
B.4
C.9
D.13
3.若代数式有意义,则实数x的取值范围是( )
A.x=0
B.x=3
C.x≠0
D.x≠3
4.下列计算正确的是( )
A.(﹣1)﹣1=1
B.(﹣1)0=0
C.|﹣1|=﹣1
D.﹣(﹣1)﹣1=1
5.下列各图中,正确画出AC边上的高的是( )
A.
B.
C.
D.
6.如图,在△ABC中,点D在BC上,AB=AD=DC,∠B=80°,则∠C的度数为( )
A.30°
B.40°
C.45°
D.60°
7.下列计算正确的有几个( )
=﹣1;=﹣1;=x+y;=2.
A.4个
B.3个
C.2个
D.1个
8.下列命题的逆命题一定成立的是( )
①对顶角相等;
②同位角相等,两直线平行;
③全等三角形的周长相等;
④能够完全重合的两个三角形全等.
A.①②③
B.①④
C.②④
D.②
二、填空题(共6小题,每小题3分,满分18分)
9.如果分式的值为零,那么x=
.
10.医学家发现了一种病毒,其长度约为0.00000029mm,用科学记数法表示为
mm.
11.如图,等腰三角形ABC中,AB=AC,∠A=44°,CD⊥AB于D,则∠DCB等于
.
12.若解分式方程产生增根,则m=
.
13.如图,在△ABC中,∠ABC=116°,若DE、FG分别垂直平分AB、BC,那么∠EBF的度数为
度.
14.观察下列各等式:,,,…根据你发现的规律,计算:=
(n为正整数).
三、解答题(本大题共9道小题,合计58分)
15.(1);
(2)+.
16.解方程:﹣=1.
17.先化简,然后从0,1,2,3中选取一个你认为符合题意的x的值代入求值.
18.如图,AD,AE分别是△ABC的高和角平分线.已知∠B=40°,∠C=50°,求∠DAE的度数.
19.如图,在△ABD和△FEC中,点B,C,D,E在同一直线上,且AB=FE,BC=DE,∠B=∠E.求证:∠ADB=∠FCE.
20.某中学组织学生到离学校30km的张家界森林公园游玩,先遣队与大队同时出发,先遣队的速度是大队的速度的1.2倍,结果先遣队比大队早到1小时,先遣队的速度是多少?大队的速度是多少?
21.如图所示,EG∥AF,AB=AC,DE=DF,求证:BE=CF.
22.在等边三角形ABC中,点P在△ABC内,点Q在△ABC外,点B,P,Q在同一条直线上,且∠ABP=∠ACQ,BP=CQ.
(1)求证:△ABP≌△ACQ;
(2)请判断△APQ是什么形状的三角形?试说明理由.
23.如图,在△ABC中,∠ACB=90°,以AC为边在△ABC外作等边三角形ACD,过点D作AC的垂线,垂足为F,延长DF交AB于点E,连接CE.
(1)求证:CE=BE.
(2)若AB=15cm,P是直线DE上的一点.则当P在何处时,PB+PC最小?并求出此时PB+PC的值.
参考答案
一、选择题(本大题共8个小题,每小题3分,满分24分.请将正确答案的字母代号填在下表中.)
1.下列代数式,不是分式的是( )
A.
B.
C.
D.
【分析】根据分式的定义判断即可.
解:一般地,如果A,B表示两个整式,并且B中含有字母,那么式子叫做分式,
∴不是分式,
故选:A.
2.已知三角形的两边长分别是4和8,那么这个三角形第三边长可能是( )
A.2
B.4
C.9
D.13
【分析】根据三角形的三边关系可得8﹣4<x<8+4,解不等式,确定x的取值范围,然后可得答案.
解:设第三边长为x,由题意得:8﹣4<x<8+4,
即4<x<12,
故选:C.
3.若代数式有意义,则实数x的取值范围是( )
A.x=0
B.x=3
C.x≠0
D.x≠3
【分析】根据分式有意义的条件列出不等式解不等式即可.
解:由题意得,x﹣3≠0,
解得,x≠3,
故选:D.
4.下列计算正确的是( )
A.(﹣1)﹣1=1
B.(﹣1)0=0
C.|﹣1|=﹣1
D.﹣(﹣1)﹣1=1
【分析】根据负整数指数幂计算A,D选项,根据零指数幂计算B选项,根据绝对值的性质计算C选项.
解:A选项,原式==﹣1,故该选项不符合题意;
B选项,(﹣1)0=1,故该选项不符合题意;
C选项,|﹣1|=1,故该选项不符合题意;
D选项,﹣(﹣1)﹣1=﹣=1,故该选项符合题意;
故选:D.
5.下列各图中,正确画出AC边上的高的是( )
A.
B.
C.
D.
【分析】根据三角形高的定义,过点B与AC边垂直,且垂足在边AC上,然后结合各选项图形解答.
解:根据三角形高线的定义,只有D选项中的BE是边AC上的高.
故选:D.
6.如图,在△ABC中,点D在BC上,AB=AD=DC,∠B=80°,则∠C的度数为( )
A.30°
B.40°
C.45°
D.60°
【分析】先根据等腰三角形的性质求出∠ADB的度数,再由平角的定义得出∠ADC的度数,根据等腰三角形的性质即可得出结论.
解:∵△ABD中,AB=AD,∠B=80°,
∴∠B=∠ADB=80°,
∴∠ADC=180°﹣∠ADB=100°,
∵AD=CD,
∴∠C===40°.
故选:B.
7.下列计算正确的有几个( )
=﹣1;=﹣1;=x+y;=2.
A.4个
B.3个
C.2个
D.1个
【分析】根据分式的基本性质判断即可.
解:根据分式的基本性质,知道前三个都不正确,
=
=
=2,
综上,正确的有1个,
故选:D.
8.下列命题的逆命题一定成立的是( )
①对顶角相等;
②同位角相等,两直线平行;
③全等三角形的周长相等;
④能够完全重合的两个三角形全等.
A.①②③
B.①④
C.②④
D.②
【分析】写出原命题的逆命题后判断正误即可.
解:①对顶角相等的逆命题为相等的角为对顶角,不成立,不符合题意;
②同位角相等,两直线平行的逆命题为两直线平行,同位角相等,成立,符合题意;
③全等三角形的周长相等的逆命题为周长相等的三角形全等,不成立,不符合题意;
④能够完全重合的两个三角形全等的逆命题为全等三角形能够完全重合,成立,符合题意,
故选:C.
二、填空题(共6小题,每小题3分,满分18分)
9.如果分式的值为零,那么x= ﹣1 .
【分析】分式的值为0的条件是:分子为0,分母不为0,两个条件需同时具备,缺一不可.据此可以解答本题.
解:如果分式的值为零,则|x|﹣1=0.
解得x=1或﹣1.
x﹣1≠0,解得x≠1,
∴x=﹣1.
故答案为﹣1.
10.医学家发现了一种病毒,其长度约为0.00000029mm,用科学记数法表示为 2.9×10﹣7 mm.
【分析】绝对值小于1的正数也可以利用科学记数法表示,一般形式为a×10﹣n,与较大数的科学记数法不同的是其所使用的是负指数幂,指数由原数左边起第一个不为零的数字前面的0的个数所决定.
解:0.00000029=2.9×10﹣7,
故答案为:2.9×10﹣7.
11.如图,等腰三角形ABC中,AB=AC,∠A=44°,CD⊥AB于D,则∠DCB等于 22° .
【分析】由等腰三角形ABC中,AB=AC,∠A=44°,根据等边对等角的性质,即可求得∠ACB的度数,又由CD⊥AB,可求得∠ACD的度数,继而求得答案.
解:∵等腰三角形ABC中,AB=AC,∠A=44°,
∴∠ACB=∠B==68°,
∵CD⊥AB,
∴∠ACD=90°﹣∠A=46°,
∴∠DCB=∠ACB﹣∠ACD=68°﹣46°=22°.
故答案为:22°.
12.若解分式方程产生增根,则m= ﹣5 .
【分析】分式方程去分母后转化为整式方程,由分式方程无解得到x=﹣4,代入整式方程即可求出m的值.
解:方程去分母得:x﹣1=m,
由题意将x=﹣4代入方程得:﹣4﹣1=m,
解得:m=﹣5.
故答案为:﹣5.
13.如图,在△ABC中,∠ABC=116°,若DE、FG分别垂直平分AB、BC,那么∠EBF的度数为
52 度.
【分析】根据三角形内角和定理求出∠A+∠C,根据线段垂直平分线的性质得到EA=EB,FB=FC,进而得出∠EBA=∠A,∠FBC=∠C,结合图形计算,得到答案.
解:在△ABC中,∠ABC=116°,
则∠A+∠C=180°﹣116°=64°,
∵DE、FG分别垂直平分AB、BC,
∴EA=EB,FB=FC,
∴∠EBA=∠A,∠FBC=∠C,
∴∠EBA+∠FBC=∠A+∠C=64°,
∴∠EBF=116°﹣64°=52°,
故答案为:52.
14.观察下列各等式:,,,…根据你发现的规律,计算:= (n为正整数).
【分析】根据题目中给出的等式,先对所求式子提出公因数2019,然后将括号内的式子分解,再加减即可.
解:
=2019×[+++…+]
=2019×(1﹣+++…+)
=2019×(1﹣)
=2019×
=,
故答案为:.
三、解答题(本大题共9道小题,合计58分)
15.(1);
(2)+.
【分析】(1)先化简有理数的乘方,零指数幂,负整数指数幂,然后再计算;
(2)先通分,然后按照同分母分式加法运算法则进行计算.
解:(1)原式=﹣(﹣1)﹣1+4
=1﹣1+4
=4;
(2)原式=+
=
=
=.
16.解方程:﹣=1.
【分析】分式方程去分母转化为整式方程,求出整式方程的解得到x的值,经检验即可得到分式方程的解.
解:去分母得:x(x+2)﹣2=x2﹣4,
去括号得:x2+2x﹣2=x2﹣4,
解得:x=﹣1,
经检验x=﹣1是分式方程的解.
17.先化简,然后从0,1,2,3中选取一个你认为符合题意的x的值代入求值.
【分析】根据分式的减法和除法可以化简题目中的式子,然后从0,1,2,3中选取一个使得原分式有意义的值代入化简后的式子即可解答本题.
解:
=÷
=
=﹣,
∵(x+3)(x﹣3)≠0,4﹣x≠0,
∴x≠±3,4,
∴x=0,1,2,
当x=0时,原式=﹣=﹣.
18.如图,AD,AE分别是△ABC的高和角平分线.已知∠B=40°,∠C=50°,求∠DAE的度数.
【分析】根据三角形的内角和可求解∠BAC的度数,结合角平分线的定义可求解∠BAE的度数,由三角形高线可求解∠BAD的度数,进而可求解.
解:(1)∵∠B=40°,∠C=50°,
∴∠BAC=180°﹣∠B﹣∠C=180°﹣40°﹣50°=90°,
∵AE是角平分线,
∴∠BAE=∠BAC=×90°=45°,
∵AD是△ABC的高,
∴∠BAD=90°﹣∠B=90°﹣40°=50°,
∴∠DAE=∠BAD﹣∠BAE=50°﹣45°=5°.
19.如图,在△ABD和△FEC中,点B,C,D,E在同一直线上,且AB=FE,BC=DE,∠B=∠E.求证:∠ADB=∠FCE.
【分析】根据等式的性质得出BD=CE,再利用SAS得出:△ABD与△FEC全等,进而得出∠ADB=∠FCE.
【解答】证明:∵BC=DE,
∴BC+CD=DE+CD,
即BD=CE,
在△ABD与△FEC中,
,
∴△ABD≌△FEC(SAS),
∴∠ADB=∠FCE.
20.某中学组织学生到离学校30km的张家界森林公园游玩,先遣队与大队同时出发,先遣队的速度是大队的速度的1.2倍,结果先遣队比大队早到1小时,先遣队的速度是多少?大队的速度是多少?
【分析】设大队的速度为xkm/h,则先遣队的速度是1.2xkm/h,利用时间=路程÷速度,结合先遣队比大队早到1小时,即可得出关于x的分式方程,解之经检验后即可得出大队的速度,再将其代入1.2x中可求出先遣队的速度.
解:设大队的速度为xkm/h,则先遣队的速度是1.2xkm/h,
依题意得:﹣=1,
解得:x=5,
经检验,x=5是原分式方程的解且符合实际,
∴1.2x=1.2×5=6.
答:先遣队的速度是6km/h,大队的速度是5km/h.
21.如图所示,EG∥AF,AB=AC,DE=DF,求证:BE=CF.
【分析】由平行线的性质得出∠GED=∠F,∠BGE=∠BCA,证出BE=EG,证明△DEG≌△DFC(ASA),由全等三角形的性质可得出EG=CF,则可得出结论.
【解答】证明:∵EG∥AF,
∴∠GED=∠F,∠BGE=∠BCA,
∵AB=AC,
∴∠B=∠BCA,
∴∠B=∠BGE,
∴BE=EG.
在△DEG和△DFC中,
,
∴△DEG≌△DFC(ASA),
∴EG=CF,
∴BE=CF.
22.在等边三角形ABC中,点P在△ABC内,点Q在△ABC外,点B,P,Q在同一条直线上,且∠ABP=∠ACQ,BP=CQ.
(1)求证:△ABP≌△ACQ;
(2)请判断△APQ是什么形状的三角形?试说明理由.
【分析】(1)根据等边三角形的性质可得AB=AC,再根据SAS证明△ABP≌△ACQ;
(2)根据全等三角形的性质得到AP=AQ,再证∠PAQ=60°,从而得出△APQ是等边三角形.
【解答】证明:(1)∵△ABC为等边三角形,
∴AB=AC,∠BAC=60°,
在△ABP和△ACQ中,
,
∴△ABP≌△ACQ(SAS),
(2)∵△ABP≌△ACQ,
∴∠BAP=∠CAQ,AP=AQ,
∵∠BAP+∠CAP=60°,
∴∠PAQ=∠CAQ+∠CAP=60°,
∴△APQ是等边三角形.
23.如图,在△ABC中,∠ACB=90°,以AC为边在△ABC外作等边三角形ACD,过点D作AC的垂线,垂足为F,延长DF交AB于点E,连接CE.
(1)求证:CE=BE.
(2)若AB=15cm,P是直线DE上的一点.则当P在何处时,PB+PC最小?并求出此时PB+PC的值.
【分析】(1)先证明DE是AC的垂直平分线,再证明DE∥BC,最后由∠ECB=∠EBC,即可证得CE=BE;
(2)连接PA,PC,由垂直平分线的性质可得PC=PA,再由两点之间线段最短即可得到所求PA+PB最小为AB的长.
解:(1)∵△ACD为等边三角形,DE⊥AC,
∴DE垂直平分AC,
∴∠AEF=∠FEC,
∵∠ACB=∠AFE=90°,
∴DE∥BC,
∴∠AEF=∠EBC,∠FEC=∠ECB,
∴∠ECB=∠EBC,
∴CE=BE;
(2)连接PA,PC,
∵DE垂直平分AC,P在DE上,
∴PC=PA,
∵两点之间线段最短,
∴当P与E重合时PA+PB最小为15
cm,
∴PB+PC最小为15
cm.
同课章节目录
