第一章 空间向量与立体几何基础达标训练 -2021-2022学年高二上学期数学人教A版(2019)选择性必修第一册(word版 含答案解析)
文档属性
| 名称 | 第一章 空间向量与立体几何基础达标训练 -2021-2022学年高二上学期数学人教A版(2019)选择性必修第一册(word版 含答案解析) |  | |
| 格式 | docx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-22 11:00:56 | ||
图片预览




文档简介
第一章
空间向量与立体几何基本达标训练题
一.选择题(共8小题)
1.若两异面直线与的方向向量分别是,0,,,,,则直线与的夹角为
A.
B.
C.
D.
2.已知向量,若,则的值为
A.1
B.
C.
D.3
3.空间点,,,,0,,,若,则的最小值为
A.1
B.2
C.3
D.4
4.已知空间向量,0,,,1,,且,则向量与的夹角为
A.
B.
C.
D.
5.设,1,,,2,,,1,,则线段的中点到点的距离为
A.
B.
C.
D.
6.在空间直角坐标系中,点是,3,在坐标平面内的射影,为坐标原点,则等于
A.
B.
C.
D.5
7.已知,,,,,,若,则实数,的值分别是
A.1,
B.,
C.1,2
D.,2
8.已知直线的一个方向向量,,,且直线过,,和,2,两点,则
A.0
B.1
C.
D.3
二.多选题(共4小题)
9.已知直线、的方向向量分别是,4,,,,,若且,则的值可以是
A.
B.
C.1
D.3
10.若,,与的夹角为,则的值为
A.17
B.
C.
D.1
11.如图,在长方体中,,,,以直线,,分别为轴、轴、轴,建立空间直角坐标系,则
A.点的坐标为,5,
B.点关于点对称的点为,8,
C.点关于直线对称的点为,5,
D.点关于平面对称的点为,5,
12.设动点在正方体上(含内部),且,当为锐角时,实数可能的取值是
A.
B.
C.
D.
三.填空题(共4小题)
13.设空间向量,2,,,,,若,则 .
14.已知空间向量分别是,的方向向量,则 ;向量与的夹角为 .
15.已知,1,,,,,则, .
16.17世纪,笛卡尔在《几何学》中,通过建立坐标系,引入点的坐标的概念,将代数对象与几何对象建立关系,从而实现了代数问题与几何问题的转化,打开了数学发展的新局面,创立了新分支——解析几何.我们知道,方程在一维空间中,表示一个点;在二维空间中,它表示一条直线,那么在三维空间中,它表示
,过点,,且法向量为的平面的方程是
.
四.解答题(共6小题)
17.如图,在四棱锥中,底面为矩形,侧棱底面,,,,为的中点.
(1)求,的值;
(2)在侧面内找一点,使平面,并求出到和的距离.
18.已知,1,,,5,,求:
(1)线段的中点坐标和长度;
(2)到,两点距离相等的点,,的坐标,,满足的条件.
19.已知:,4,,,,,,,,,,求:
(1),,;
(2)与所成角的余弦值.
20.如图,直三棱柱底面中,,,棱,是的中点.
(1)求,的值;
(2)求证:.
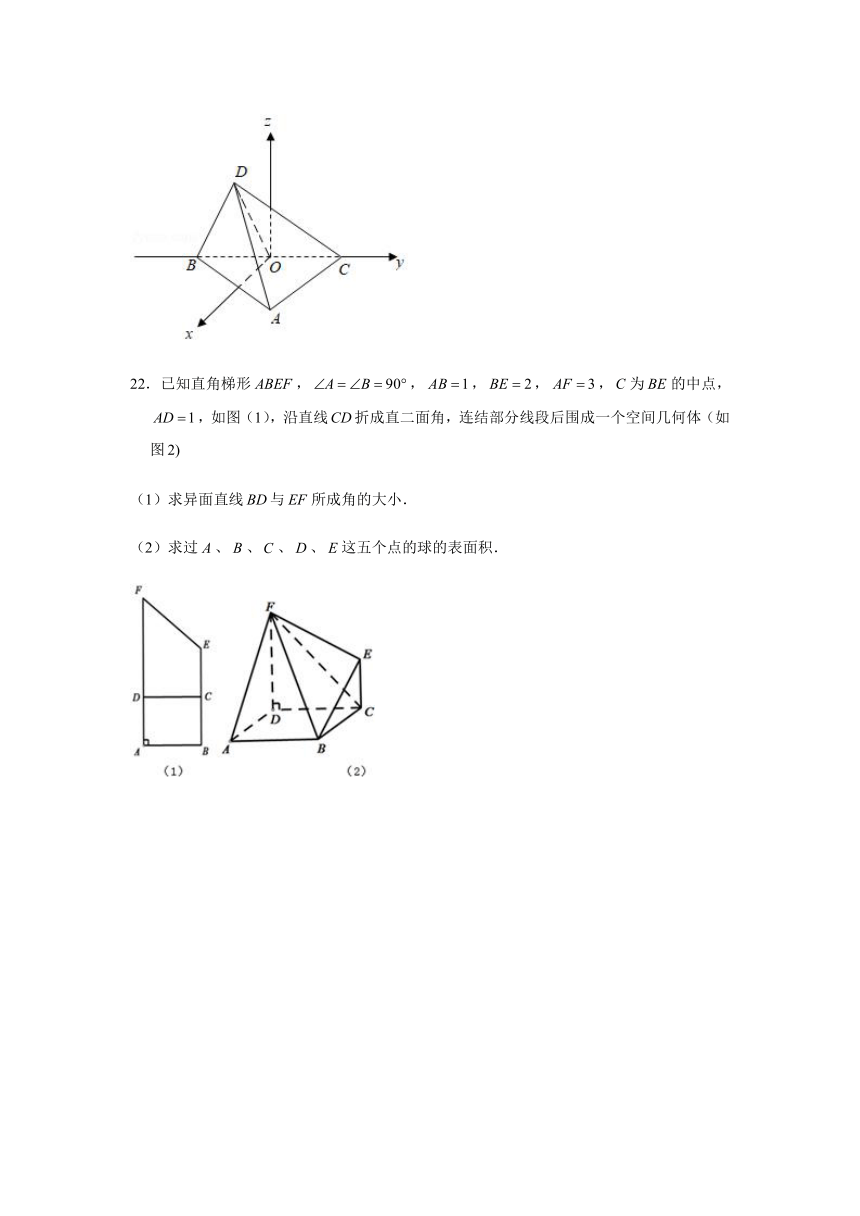
21.如图,,原点是的中点,点的坐标为,,,点在平面上,且,.
(1)求向量的坐标.
(2)求与的夹角的余弦值.
22.已知直角梯形,,,,,为的中点,,如图(1),沿直线折成直二面角,连结部分线段后围成一个空间几何体(如图
(1)求异面直线与所成角的大小.
(2)求过、、、、这五个点的球的表面积.
参考答案与试题解析
一.选择题(共8小题)
1.若两异面直线与的方向向量分别是,0,,,,,则直线与的夹角为
A.
B.
C.
D.
解:,0,,,,,
可得,
,,
则,,
由,,可得,,
可得直线与的夹角为,
故选:.
2.已知向量,若,则的值为
A.1
B.
C.
D.3
解:,
,解得.
故选:.
3.空间点,,,,0,,,若,则的最小值为
A.1
B.2
C.3
D.4
解:空间点,,,,0,,,,
是以为球心,1为半径的球上的点,
,.
的最小值为:.
故选:.
4.已知空间向量,0,,,1,,且,则向量与的夹角为
A.
B.
C.
D.
解:,
解得;
又,,1,,
,,
且,,,
与的夹角为.
故选:.
5.设,1,,,2,,,1,,则线段的中点到点的距离为
A.
B.
C.
D.
解:.
.
.
故选:.
6.在空间直角坐标系中,点是,3,在坐标平面内的射影,为坐标原点,则等于
A.
B.
C.
D.5
解:空间直角坐标系中,则点,3,在坐标平面内的射影是,3,,
所以.
故选:.
7.已知,,,,,,若,则实数,的值分别是
A.1,
B.,
C.1,2
D.,2
解:,,,,,,
若,则,
解得,.
故选:.
8.已知直线的一个方向向量,,,且直线过,,和,2,两点,则
A.0
B.1
C.
D.3
解:,,.
.
,,.
解得,.
.
故选:.
二.多选题(共4小题)
9.已知直线、的方向向量分别是,4,,,,,若且,则的值可以是
A.
B.
C.1
D.3
解:直线、的方向向量分别是,4,,,,,且,
,解得,
或,
或.
故选:.
10.若,,与的夹角为,则的值为
A.17
B.
C.
D.1
解:,,与的夹角为,
,
解得或.
故选:.
11.如图,在长方体中,,,,以直线,,分别为轴、轴、轴,建立空间直角坐标系,则
A.点的坐标为,5,
B.点关于点对称的点为,8,
C.点关于直线对称的点为,5,
D.点关于平面对称的点为,5,
解:由图形及其已知可得:点的坐标为,5,,点,5,关于点对称的点为,5,,
点关于直线对称的点为,5,,
点,5,关于平面对称的点为,5,.
因此正确.
故选:.
12.设动点在正方体上(含内部),且,当为锐角时,实数可能的取值是
A.
B.
C.
D.
解:由题设可知,建立如图所示的空间直角坐标系,设正方体的棱长为1,
则,0,,,1,,,1,,,0,
由,1,,得,,,
所以,,,0,,,,
,,,1,,,,
所以为锐角等价于,
则等价于,
即,
又由,解可得
因此,的取值范围是,,
分析选项:,,,,
故选:.
三.填空题(共4小题)
13.设空间向量,2,,,,,若,则 .
解:因为空间向量,2,,,,,且,
所以,
即,,,2,,
可得,解得,,
所以,2,,,,,
则,6,,
所以.
故答案为:9.
14.已知空间向量分别是,的方向向量,则 ;向量与的夹角为 .
解:根据题意,空间向量,
则,0,,则,
,,,
则,,
又由,,则,,
故答案为:,.
15.已知,1,,,,,则, .
解:,1,,,,,
,.
故答案为:.
16.17世纪,笛卡尔在《几何学》中,通过建立坐标系,引入点的坐标的概念,将代数对象与几何对象建立关系,从而实现了代数问题与几何问题的转化,打开了数学发展的新局面,创立了新分支——解析几何.我们知道,方程在一维空间中,表示一个点;在二维空间中,它表示一条直线,那么在三维空间中,它表示
,过点,,且法向量为的平面的方程是
.
解:在三维空间中,表示过,0,且与平面平行的平面.
设平面上任意一点的坐标为,,,则.
由得,整理得.
故答案为:平面;.
四.解答题(共6小题)
17.如图,在四棱锥中,底面为矩形,侧棱底面,,,,为的中点.
(1)求,的值;
(2)在侧面内找一点,使平面,并求出到和的距离.
解:(1)在四棱锥中,底面为矩形
侧棱底面,,,,为的中点.
以为原点,为轴,为轴,为轴,建立空间直角坐标系,
则,0,,,1,,,0,,,0,,
,,
.
(2)设在侧面内找一点,0,,使平面,
,1,,,,,,,,
,0,,,
,解得,,
,0,,
到的距离为1,
到的距离为.
18.已知,1,,,5,,求:
(1)线段的中点坐标和长度;
(2)到,两点距离相等的点,,的坐标,,满足的条件.
解:(1),1,,,5,,
中点坐标,3,.,4,,
.
(2),1,,,5,,,,,
由得:
,
整理得:.
19.已知:,4,,,,,,,,,,求:
(1),,;
(2)与所成角的余弦值.
解:(1),
,
解得,,
故,4,,,,,
又因为,所以,即,解得,
故,,
(2)由(1)可得,2,,,,,
设向量与所成的角为,
则
20.如图,直三棱柱底面中,,,棱,是的中点.
(1)求,的值;
(2)求证:.
解:(1)以为原点,,,所在直线分别为,,轴,建立空间直角坐标系,
,0,,,1,,,0,,,1,,
,,,,1,,
,.
证明:(2),0,,,1,,,0,,,
,1,,,,
,
.
21.如图,,原点是的中点,点的坐标为,,,点在平面上,且,.
(1)求向量的坐标.
(2)求与的夹角的余弦值.
解:(1)过作于,则,
,
的坐标为,,,
又,1,,,,.
(2)依题设有点坐标为,,,
,,2,,
则与的夹角的余弦值:
.
22.已知直角梯形,,,,,为的中点,,如图(1),沿直线折成直二面角,连结部分线段后围成一个空间几何体(如图
(1)求异面直线与所成角的大小.
(2)求过、、、、这五个点的球的表面积.
解:(1)以点为坐标原点,分别以,,所在直线为轴,轴,轴建立空间直角坐标系,
,0,,,0,,,1,,,1,,,1,,,0,
,1,,,,,
设异面直线与所成角为,
则,
,
异面直线与所成角的大小为.
(2)连结,取中点为,连结,,,,,
由已知得,
所以长为所求球的半径,
,,,,
.
过、、、、这五个点的球的表面积:
.
空间向量与立体几何基本达标训练题
一.选择题(共8小题)
1.若两异面直线与的方向向量分别是,0,,,,,则直线与的夹角为
A.
B.
C.
D.
2.已知向量,若,则的值为
A.1
B.
C.
D.3
3.空间点,,,,0,,,若,则的最小值为
A.1
B.2
C.3
D.4
4.已知空间向量,0,,,1,,且,则向量与的夹角为
A.
B.
C.
D.
5.设,1,,,2,,,1,,则线段的中点到点的距离为
A.
B.
C.
D.
6.在空间直角坐标系中,点是,3,在坐标平面内的射影,为坐标原点,则等于
A.
B.
C.
D.5
7.已知,,,,,,若,则实数,的值分别是
A.1,
B.,
C.1,2
D.,2
8.已知直线的一个方向向量,,,且直线过,,和,2,两点,则
A.0
B.1
C.
D.3
二.多选题(共4小题)
9.已知直线、的方向向量分别是,4,,,,,若且,则的值可以是
A.
B.
C.1
D.3
10.若,,与的夹角为,则的值为
A.17
B.
C.
D.1
11.如图,在长方体中,,,,以直线,,分别为轴、轴、轴,建立空间直角坐标系,则
A.点的坐标为,5,
B.点关于点对称的点为,8,
C.点关于直线对称的点为,5,
D.点关于平面对称的点为,5,
12.设动点在正方体上(含内部),且,当为锐角时,实数可能的取值是
A.
B.
C.
D.
三.填空题(共4小题)
13.设空间向量,2,,,,,若,则 .
14.已知空间向量分别是,的方向向量,则 ;向量与的夹角为 .
15.已知,1,,,,,则, .
16.17世纪,笛卡尔在《几何学》中,通过建立坐标系,引入点的坐标的概念,将代数对象与几何对象建立关系,从而实现了代数问题与几何问题的转化,打开了数学发展的新局面,创立了新分支——解析几何.我们知道,方程在一维空间中,表示一个点;在二维空间中,它表示一条直线,那么在三维空间中,它表示
,过点,,且法向量为的平面的方程是
.
四.解答题(共6小题)
17.如图,在四棱锥中,底面为矩形,侧棱底面,,,,为的中点.
(1)求,的值;
(2)在侧面内找一点,使平面,并求出到和的距离.
18.已知,1,,,5,,求:
(1)线段的中点坐标和长度;
(2)到,两点距离相等的点,,的坐标,,满足的条件.
19.已知:,4,,,,,,,,,,求:
(1),,;
(2)与所成角的余弦值.
20.如图,直三棱柱底面中,,,棱,是的中点.
(1)求,的值;
(2)求证:.
21.如图,,原点是的中点,点的坐标为,,,点在平面上,且,.
(1)求向量的坐标.
(2)求与的夹角的余弦值.
22.已知直角梯形,,,,,为的中点,,如图(1),沿直线折成直二面角,连结部分线段后围成一个空间几何体(如图
(1)求异面直线与所成角的大小.
(2)求过、、、、这五个点的球的表面积.
参考答案与试题解析
一.选择题(共8小题)
1.若两异面直线与的方向向量分别是,0,,,,,则直线与的夹角为
A.
B.
C.
D.
解:,0,,,,,
可得,
,,
则,,
由,,可得,,
可得直线与的夹角为,
故选:.
2.已知向量,若,则的值为
A.1
B.
C.
D.3
解:,
,解得.
故选:.
3.空间点,,,,0,,,若,则的最小值为
A.1
B.2
C.3
D.4
解:空间点,,,,0,,,,
是以为球心,1为半径的球上的点,
,.
的最小值为:.
故选:.
4.已知空间向量,0,,,1,,且,则向量与的夹角为
A.
B.
C.
D.
解:,
解得;
又,,1,,
,,
且,,,
与的夹角为.
故选:.
5.设,1,,,2,,,1,,则线段的中点到点的距离为
A.
B.
C.
D.
解:.
.
.
故选:.
6.在空间直角坐标系中,点是,3,在坐标平面内的射影,为坐标原点,则等于
A.
B.
C.
D.5
解:空间直角坐标系中,则点,3,在坐标平面内的射影是,3,,
所以.
故选:.
7.已知,,,,,,若,则实数,的值分别是
A.1,
B.,
C.1,2
D.,2
解:,,,,,,
若,则,
解得,.
故选:.
8.已知直线的一个方向向量,,,且直线过,,和,2,两点,则
A.0
B.1
C.
D.3
解:,,.
.
,,.
解得,.
.
故选:.
二.多选题(共4小题)
9.已知直线、的方向向量分别是,4,,,,,若且,则的值可以是
A.
B.
C.1
D.3
解:直线、的方向向量分别是,4,,,,,且,
,解得,
或,
或.
故选:.
10.若,,与的夹角为,则的值为
A.17
B.
C.
D.1
解:,,与的夹角为,
,
解得或.
故选:.
11.如图,在长方体中,,,,以直线,,分别为轴、轴、轴,建立空间直角坐标系,则
A.点的坐标为,5,
B.点关于点对称的点为,8,
C.点关于直线对称的点为,5,
D.点关于平面对称的点为,5,
解:由图形及其已知可得:点的坐标为,5,,点,5,关于点对称的点为,5,,
点关于直线对称的点为,5,,
点,5,关于平面对称的点为,5,.
因此正确.
故选:.
12.设动点在正方体上(含内部),且,当为锐角时,实数可能的取值是
A.
B.
C.
D.
解:由题设可知,建立如图所示的空间直角坐标系,设正方体的棱长为1,
则,0,,,1,,,1,,,0,
由,1,,得,,,
所以,,,0,,,,
,,,1,,,,
所以为锐角等价于,
则等价于,
即,
又由,解可得
因此,的取值范围是,,
分析选项:,,,,
故选:.
三.填空题(共4小题)
13.设空间向量,2,,,,,若,则 .
解:因为空间向量,2,,,,,且,
所以,
即,,,2,,
可得,解得,,
所以,2,,,,,
则,6,,
所以.
故答案为:9.
14.已知空间向量分别是,的方向向量,则 ;向量与的夹角为 .
解:根据题意,空间向量,
则,0,,则,
,,,
则,,
又由,,则,,
故答案为:,.
15.已知,1,,,,,则, .
解:,1,,,,,
,.
故答案为:.
16.17世纪,笛卡尔在《几何学》中,通过建立坐标系,引入点的坐标的概念,将代数对象与几何对象建立关系,从而实现了代数问题与几何问题的转化,打开了数学发展的新局面,创立了新分支——解析几何.我们知道,方程在一维空间中,表示一个点;在二维空间中,它表示一条直线,那么在三维空间中,它表示
,过点,,且法向量为的平面的方程是
.
解:在三维空间中,表示过,0,且与平面平行的平面.
设平面上任意一点的坐标为,,,则.
由得,整理得.
故答案为:平面;.
四.解答题(共6小题)
17.如图,在四棱锥中,底面为矩形,侧棱底面,,,,为的中点.
(1)求,的值;
(2)在侧面内找一点,使平面,并求出到和的距离.
解:(1)在四棱锥中,底面为矩形
侧棱底面,,,,为的中点.
以为原点,为轴,为轴,为轴,建立空间直角坐标系,
则,0,,,1,,,0,,,0,,
,,
.
(2)设在侧面内找一点,0,,使平面,
,1,,,,,,,,
,0,,,
,解得,,
,0,,
到的距离为1,
到的距离为.
18.已知,1,,,5,,求:
(1)线段的中点坐标和长度;
(2)到,两点距离相等的点,,的坐标,,满足的条件.
解:(1),1,,,5,,
中点坐标,3,.,4,,
.
(2),1,,,5,,,,,
由得:
,
整理得:.
19.已知:,4,,,,,,,,,,求:
(1),,;
(2)与所成角的余弦值.
解:(1),
,
解得,,
故,4,,,,,
又因为,所以,即,解得,
故,,
(2)由(1)可得,2,,,,,
设向量与所成的角为,
则
20.如图,直三棱柱底面中,,,棱,是的中点.
(1)求,的值;
(2)求证:.
解:(1)以为原点,,,所在直线分别为,,轴,建立空间直角坐标系,
,0,,,1,,,0,,,1,,
,,,,1,,
,.
证明:(2),0,,,1,,,0,,,
,1,,,,
,
.
21.如图,,原点是的中点,点的坐标为,,,点在平面上,且,.
(1)求向量的坐标.
(2)求与的夹角的余弦值.
解:(1)过作于,则,
,
的坐标为,,,
又,1,,,,.
(2)依题设有点坐标为,,,
,,2,,
则与的夹角的余弦值:
.
22.已知直角梯形,,,,,为的中点,,如图(1),沿直线折成直二面角,连结部分线段后围成一个空间几何体(如图
(1)求异面直线与所成角的大小.
(2)求过、、、、这五个点的球的表面积.
解:(1)以点为坐标原点,分别以,,所在直线为轴,轴,轴建立空间直角坐标系,
,0,,,0,,,1,,,1,,,1,,,0,
,1,,,,,
设异面直线与所成角为,
则,
,
异面直线与所成角的大小为.
(2)连结,取中点为,连结,,,,,
由已知得,
所以长为所求球的半径,
,,,,
.
过、、、、这五个点的球的表面积:
.
