2021-2022学年九年级数学人教版上册22.2一元二次方程与二次函数综合能力提升习题(word版、含图片答案)
文档属性
| 名称 | 2021-2022学年九年级数学人教版上册22.2一元二次方程与二次函数综合能力提升习题(word版、含图片答案) |  | |
| 格式 | zip | ||
| 文件大小 | 897.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-21 09:29:25 | ||
图片预览

文档简介
二次函数与一元二次方程
1.关于的函数图象若与轴仅有一个公共点,则的取值是
;若与轴有公共点,则的取值范围是
.
2.关于的函数图象若与轴只有一个公共点,则的值是
;若与轴没有公共点,则的范围是
.
3.抛物线在直线上裁得的线段长度为
;抛物线的图象在直线的图象上方的部分(不含交点)所对应的的范围是
;抛物线的图象在直线的图象下方的部分(不含交点)所对应的范围是
.
4.已知抛物线的图象与轴交于,两点,则关于的方程的解为
;关于的不等式的解集是
;关于的不等式的解集是
.
5.已知抛物线()的对称轴为,与轴的一个交点为.若关于的一元二次方程有整数根,则的值有
.
A.
2个
B.
3个
C.
4个
D.
5个
6.如图,一次函数与二次函数的图象相交于,两点,则关于的不等式解集为
;关于的不等式解集为
.
7.如图,已知二次函数()与一次函数()图象相交于点,,则能使成立的的取值范围是
.
8.如图,抛物线的图象与轴交于两点,顶点为点.当为等腰直角三角形时,的值为
;当为等边三角形时,的值为
.
9.已知抛物线与轴交于两点,若线段,则的取值范围为
.
10.已知抛物线与直线相交于两点,当时,的取值范围
.
11.已知抛物线与轴的一个交点在和两点之间(不含
两点),则的取值范围是
.
12.已知关于的一元二次方程的两实根分别满足,则的取值范围是
.
13.已知关于的一元二次方程的两实根分别满足,,则的取值范围是
.
14.已知点为抛物线的顶点,直线分别交轴正半轴,轴于点.
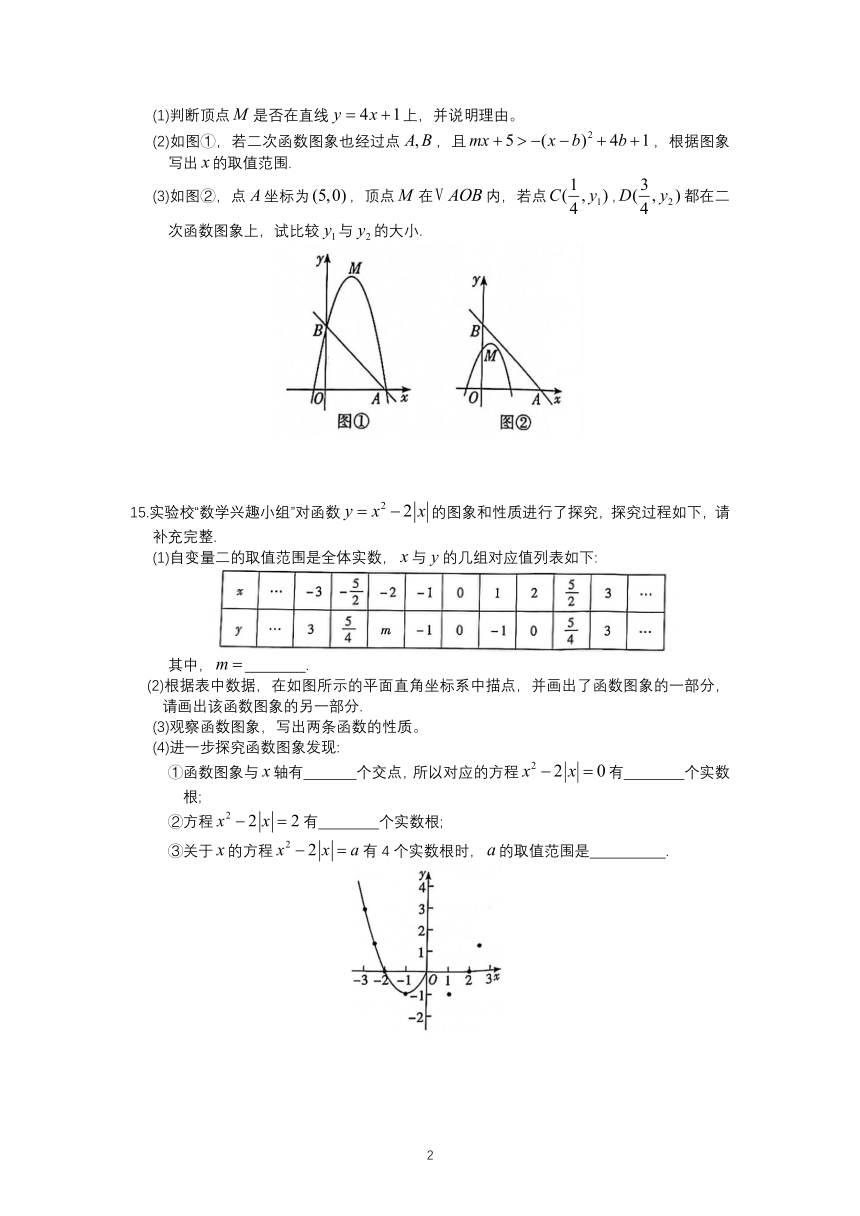
(1)判断顶点是否在直线上,并说明理由。
(2)如图①,若二次函数图象也经过点,且,根据图象写出的取值范围.
(3)如图②,点坐标为,顶点在内,若点,都在二次函数图象上,试比较与的大小.
15.实验校“数学兴趣小组”对函数的图象和性质进行了探究,探究过程如下,请补充完整.
(1)自变量二的取值范围是全体实数,与的几组对应值列表如下:
其中,
.
(2)根据表中数据,在如图所示的平面直角坐标系中描点,并画出了函数图象的一部分,请画出该函数图象的另一部分.
(3)观察函数图象,写出两条函数的性质。
(4)进一步探究函数图象发现:
①函数图象与轴有
个交点,所以对应的方程有
个实数根;
②方程有
个实数根;
③关于的方程有4个实数根时,的取值范围是
.
2
1.关于的函数图象若与轴仅有一个公共点,则的取值是
;若与轴有公共点,则的取值范围是
.
2.关于的函数图象若与轴只有一个公共点,则的值是
;若与轴没有公共点,则的范围是
.
3.抛物线在直线上裁得的线段长度为
;抛物线的图象在直线的图象上方的部分(不含交点)所对应的的范围是
;抛物线的图象在直线的图象下方的部分(不含交点)所对应的范围是
.
4.已知抛物线的图象与轴交于,两点,则关于的方程的解为
;关于的不等式的解集是
;关于的不等式的解集是
.
5.已知抛物线()的对称轴为,与轴的一个交点为.若关于的一元二次方程有整数根,则的值有
.
A.
2个
B.
3个
C.
4个
D.
5个
6.如图,一次函数与二次函数的图象相交于,两点,则关于的不等式解集为
;关于的不等式解集为
.
7.如图,已知二次函数()与一次函数()图象相交于点,,则能使成立的的取值范围是
.
8.如图,抛物线的图象与轴交于两点,顶点为点.当为等腰直角三角形时,的值为
;当为等边三角形时,的值为
.
9.已知抛物线与轴交于两点,若线段,则的取值范围为
.
10.已知抛物线与直线相交于两点,当时,的取值范围
.
11.已知抛物线与轴的一个交点在和两点之间(不含
两点),则的取值范围是
.
12.已知关于的一元二次方程的两实根分别满足,则的取值范围是
.
13.已知关于的一元二次方程的两实根分别满足,,则的取值范围是
.
14.已知点为抛物线的顶点,直线分别交轴正半轴,轴于点.
(1)判断顶点是否在直线上,并说明理由。
(2)如图①,若二次函数图象也经过点,且,根据图象写出的取值范围.
(3)如图②,点坐标为,顶点在内,若点,都在二次函数图象上,试比较与的大小.
15.实验校“数学兴趣小组”对函数的图象和性质进行了探究,探究过程如下,请补充完整.
(1)自变量二的取值范围是全体实数,与的几组对应值列表如下:
其中,
.
(2)根据表中数据,在如图所示的平面直角坐标系中描点,并画出了函数图象的一部分,请画出该函数图象的另一部分.
(3)观察函数图象,写出两条函数的性质。
(4)进一步探究函数图象发现:
①函数图象与轴有
个交点,所以对应的方程有
个实数根;
②方程有
个实数根;
③关于的方程有4个实数根时,的取值范围是
.
2
同课章节目录
