人教版七年级数学1.5.1有理数的乘方
文档属性
| 名称 | 人教版七年级数学1.5.1有理数的乘方 |  | |
| 格式 | zip | ||
| 文件大小 | 652.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-07-09 15:04:39 | ||
图片预览






文档简介
(共18张PPT)
练习一(课前测评)
1、边长为 的正方形的面积为 ;
2、棱长为 的正方体的体积为 ;
3、(-2)×(-2)×(-2)= ;
4、(-1)×(-2)×(-3)×(-4)×5= ;
5、(-1)×(-1)×(-1)×(-1)×(-1)= 。
返回
下一张
上一张
退出
-8
120
-1
把一张纸
返回
下一张
上一张
退出
若对折100次,算式中有几个2相乘?
对折2次可裁成4张,即2×2张;
对折3次可裁成8张,即2×2×2张;
问题:
若对折10次可裁成几张?请用一个算式表示(不用算出结果)
对折10次裁成的张数用以下算式计算2×2×2×2×2×2×2×2×2×2
是一个有10个2相乘的乘积式;
对折100次裁成的张数,可用算式
计算,在这个积中有100个2相乘。这么长的算式有简单的记法吗?
返回
下一张
上一张
退出
2×2×2×……×2×2×2
{
100个
2个 相加可记为:
3个 相加可为:
4个 相加可为:
个 相加可记为:
边长为 的正方形的面积可记为:
那么4个 相乘可记为:
棱长为 的正方体的体积可记为:
个 相乘又可记为:
返回
下一张
上一张
退出
{
n个
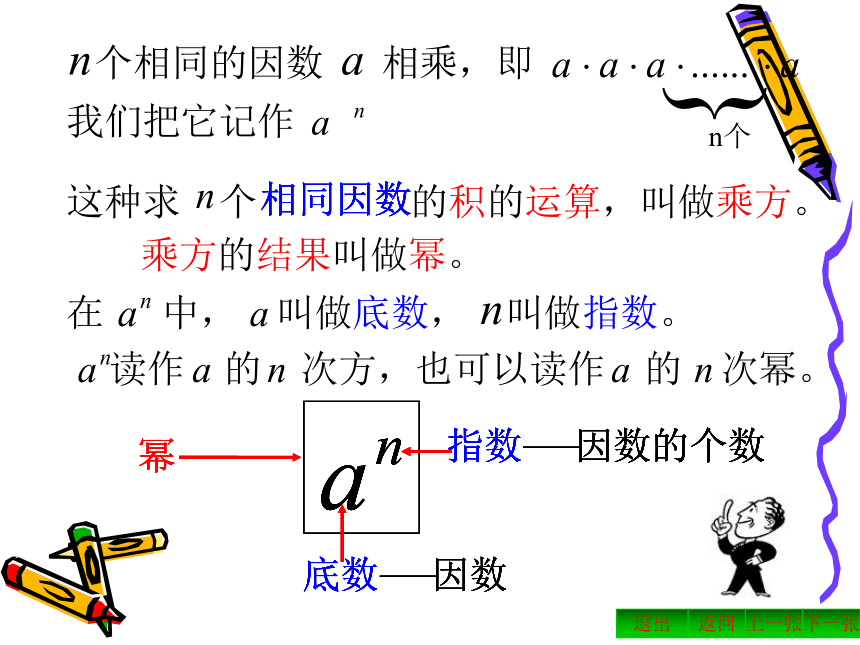
这种求 个 的积的运算,叫做乘方。
乘方的结果叫做幂。
在 中, 叫做底数, 叫做指数。
幂
底数
因数
指数
因数的个数
读作 的 次方,也可以读作 的 次幂。
幂
幂
幂
幂
幂
指数
因数的个数
指数
因数的个数
指数
因数的个数
指数
因数的个数
指数
因数的个数
底数
因数
底数
因数
底数
因数
底数
因数
底数
因数
相同因数
相同因数
相同因数
相同因数
相同因数
返回
下一张
上一张
退出
个相同的因数 相乘,即
我们把它记作
{
n个
口答练习一
1)在 中,12是 数,10是
数,读作 ;
2) 的底数是 ,指数是 ,读作 ;
返回
下一张
上一张
退出
7
的7次方
底
指
12的10次方
3)在 中,-3是 数,16是 数,读作 ; 4)在 中,底数是 ;指数是 ;读作 ;
底
指
-3的16次方
17
返回
下一张
上一张
退出
的17次方
5)5看成幂的话,底数是 ,指数是 ,可读作 ; 6) 看成幂的话,底数是 ,指数是 ,可读作 ;
幂
指数
底数
返回
下一张
上一张
退出
5
1
5的一次方
1
的一次方
1
a
幂
指数
底数
练习二
一、把下列乘法式子写成乘方的形式:
1、1×1×1×1×1×1×1= ;
2、3×3×3×3×3= ;
3、(-3)×(-3)×(-3)×(-3)= ;
4、 = ;
返回
下一张
上一张
退出
二、把下列乘方写成乘法的形式:
1、 = ;
2、 = ;
3、 = ;
返回
下一张
上一张
退出
思考:用乘方式子怎么表示 的相反数?
-
答案:
练习三
判断下列各题是否正确:
( )① ;
( )② ;
( )③ ;
( )④
返回
下一张
上一张
退出
对
错
错
错
例1计算:
解:
思考:例1的两个幂,底数都是负数,为什么这两个幂一个是正数而另一个是负数呢?是由什么数来确定它们的正负呢?
当底数是负数时,幂的正负由指数确定,指数是偶数时,幂是正数;指数是奇数时,幂是负数。
如果幂的底数正数,那么这个幂有可能是负数吗?
不可能!正数的任何次幂是都是正数
返回
下一张
上一张
退出
幂的性质:正数的任何次幂都是正数;负数的奇次幂是负数,负数的偶次幂是正数。0的任何次幂是0。
返回
下一张
上一张
退出
正
负
口答练习二
1) 是 (填“正”或“负”)数;
2) 是 (填“正”或“负”)数;
3) = ;
4) = ;
1
1
练习四
计算:(7~8选做)
1、 = ; 2、 = ;
3、 = ; 4、 = ;
5、 = ; 6、 = ;
7、 = ; 8、 = .
1
-1
25
-0.001
1
-27
-1
返回
下一张
上一张
退出
(其中n为正整数)
小结
1、乘方是特殊的乘法运算,所谓特殊就是所乘的因数是相同的;
返回
下一张
上一张
退出
2、幂是乘方运算的结果;正数的任何次幂是正数,负数的奇次幂是负数,负数的偶次幂是正数;0的任何次幂是0。
3、进行乘方运算应先确定符号后再计算。
目标检测
1、在 中,底数是 ,指数 ,
2、 读做 ;
3、 的结果是 数(填“正”或“负”);
4、计算: = ;
5、计算: = ;
返回
下一张
上一张
退出
4
6
-4的7次方或-4的7次幂
负
-8
练习一(课前测评)
1、边长为 的正方形的面积为 ;
2、棱长为 的正方体的体积为 ;
3、(-2)×(-2)×(-2)= ;
4、(-1)×(-2)×(-3)×(-4)×5= ;
5、(-1)×(-1)×(-1)×(-1)×(-1)= 。
返回
下一张
上一张
退出
-8
120
-1
把一张纸
返回
下一张
上一张
退出
若对折100次,算式中有几个2相乘?
对折2次可裁成4张,即2×2张;
对折3次可裁成8张,即2×2×2张;
问题:
若对折10次可裁成几张?请用一个算式表示(不用算出结果)
对折10次裁成的张数用以下算式计算2×2×2×2×2×2×2×2×2×2
是一个有10个2相乘的乘积式;
对折100次裁成的张数,可用算式
计算,在这个积中有100个2相乘。这么长的算式有简单的记法吗?
返回
下一张
上一张
退出
2×2×2×……×2×2×2
{
100个
2个 相加可记为:
3个 相加可为:
4个 相加可为:
个 相加可记为:
边长为 的正方形的面积可记为:
那么4个 相乘可记为:
棱长为 的正方体的体积可记为:
个 相乘又可记为:
返回
下一张
上一张
退出
{
n个
这种求 个 的积的运算,叫做乘方。
乘方的结果叫做幂。
在 中, 叫做底数, 叫做指数。
幂
底数
因数
指数
因数的个数
读作 的 次方,也可以读作 的 次幂。
幂
幂
幂
幂
幂
指数
因数的个数
指数
因数的个数
指数
因数的个数
指数
因数的个数
指数
因数的个数
底数
因数
底数
因数
底数
因数
底数
因数
底数
因数
相同因数
相同因数
相同因数
相同因数
相同因数
返回
下一张
上一张
退出
个相同的因数 相乘,即
我们把它记作
{
n个
口答练习一
1)在 中,12是 数,10是
数,读作 ;
2) 的底数是 ,指数是 ,读作 ;
返回
下一张
上一张
退出
7
的7次方
底
指
12的10次方
3)在 中,-3是 数,16是 数,读作 ; 4)在 中,底数是 ;指数是 ;读作 ;
底
指
-3的16次方
17
返回
下一张
上一张
退出
的17次方
5)5看成幂的话,底数是 ,指数是 ,可读作 ; 6) 看成幂的话,底数是 ,指数是 ,可读作 ;
幂
指数
底数
返回
下一张
上一张
退出
5
1
5的一次方
1
的一次方
1
a
幂
指数
底数
练习二
一、把下列乘法式子写成乘方的形式:
1、1×1×1×1×1×1×1= ;
2、3×3×3×3×3= ;
3、(-3)×(-3)×(-3)×(-3)= ;
4、 = ;
返回
下一张
上一张
退出
二、把下列乘方写成乘法的形式:
1、 = ;
2、 = ;
3、 = ;
返回
下一张
上一张
退出
思考:用乘方式子怎么表示 的相反数?
-
答案:
练习三
判断下列各题是否正确:
( )① ;
( )② ;
( )③ ;
( )④
返回
下一张
上一张
退出
对
错
错
错
例1计算:
解:
思考:例1的两个幂,底数都是负数,为什么这两个幂一个是正数而另一个是负数呢?是由什么数来确定它们的正负呢?
当底数是负数时,幂的正负由指数确定,指数是偶数时,幂是正数;指数是奇数时,幂是负数。
如果幂的底数正数,那么这个幂有可能是负数吗?
不可能!正数的任何次幂是都是正数
返回
下一张
上一张
退出
幂的性质:正数的任何次幂都是正数;负数的奇次幂是负数,负数的偶次幂是正数。0的任何次幂是0。
返回
下一张
上一张
退出
正
负
口答练习二
1) 是 (填“正”或“负”)数;
2) 是 (填“正”或“负”)数;
3) = ;
4) = ;
1
1
练习四
计算:(7~8选做)
1、 = ; 2、 = ;
3、 = ; 4、 = ;
5、 = ; 6、 = ;
7、 = ; 8、 = .
1
-1
25
-0.001
1
-27
-1
返回
下一张
上一张
退出
(其中n为正整数)
小结
1、乘方是特殊的乘法运算,所谓特殊就是所乘的因数是相同的;
返回
下一张
上一张
退出
2、幂是乘方运算的结果;正数的任何次幂是正数,负数的奇次幂是负数,负数的偶次幂是正数;0的任何次幂是0。
3、进行乘方运算应先确定符号后再计算。
目标检测
1、在 中,底数是 ,指数 ,
2、 读做 ;
3、 的结果是 数(填“正”或“负”);
4、计算: = ;
5、计算: = ;
返回
下一张
上一张
退出
4
6
-4的7次方或-4的7次幂
负
-8
